2. 安徽省气象台
2. Anhui Meteorological Bureau
59型探空仪在我国使用已几十年。因温度滞后和太阳辐射等原因, 其测得的高层温度和高度资料存在较大的正偏差和随机误差。尽管2000年中国气象科学研究院大气探测研究所曾组织有关人员对59型探空仪观测资料实施系统性偏差订正(注:本文使用59型探空仪温度资料都是经过系统性偏差订正的, 在300hPa附近, 订正值超过1℃), 基本消除较大正偏差, 但无法根本解决资料质量问题。为提高我国探空资料质量, 我国自行研制的L波段探空仪已逐步投入使用。到2005年6月, 已有36个探空站使用L波段探空仪。但是任何观测资料均有观测误差, 除与探空仪性能有关外、还与观测员本身及相关软件等因素有关。及时了解其观测误差量级和分布特征对合理使用观测资料和进一步改进观测仪器至关重要。
最直接的观测误差估计方法是用多种无线电探空仪同时同地多次施放的直接对比方法[1]。因大气状态的真值无法测定, 难以判定那种探测资料最精确。通常将多种探测资料平均值作为参照值, 偏离参照值最小的探测资料被确认为最精确。该方法虽能直观显现出各种探测资料之间的差异。但若大多数探测资料具有相似特性, 它们则控制了参照值, 真正精度较高的探测资料会因偏离参照值而被认为是较差的, 而且把不同国家或地区的各种探空仪同时同地多次施放也有困难。定性评估观测资料质量的另一种途径是借助数值预报系统的背景场, 用观测资料减模式背景场的差(简称OMB)的平均偏差和标准差估算观测误差[2]。OMB的平均偏差和标准差均包含观测误差和背景场误差两部分, 并受仪器类型、地形、纬度及气候等因子的影响, 难以用OMB平均偏差和标准差的大小定量地估算观测资料的系统性误差和随机误差。
贝塞尔函数拟合法能从OMB协方差中分解出观测误差均方差, 即随机误差[3]。虽然此法得出的观测误差仍含有模式代表性误差, 但比OMB标准差要精确得多。
1 观测误差分析方法我们没有多种无线电探空仪同时同地多次施放的观测资料。为了解L波段探空仪观测质量, 应用国家气象中心观测资料质量监测评估系统[4], 运用CQC质量控制方案[5]对观测资料进行质量控制排除异常值; 以T213的6小时预报场为背景场, 分别统计L波段、59型和美国区域探空仪温度OMB平均偏差和标准差; 再利用贝塞尔函数拟合理论从OMB中分离观测误差; 对比三种探空仪的计算结果, 分析L波段探测温度资料随机误差特性。
贝塞尔函数拟合法假设预报和观测误差无偏、观测误差与背景场误差不相关、不同站点之间观测误差不相关和背景场误差在水平方向均匀且各向同性, 则背景场误差协方差为:
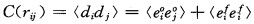
|
(1) |
(1) 式中r为i、j两观测点间的距离; ef为背景场误差; eo为观测误差; d=eo-ef, 当rij=0时, 为〈didj〉背景场误差方差和观测误差方差之和, rij ≠0时, 〈 didj 〉= 〈eifejf〉为背景场误差协方差, 且为rij的函数。由rij ≠ 0的点可以拟合出背景误差协方差曲线。
在半无限空间0 ≤ r < ∞, Czz (r)的贝塞尔函数拟合形式为:
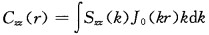
|
(2) |
其中J0(·)是0阶贝塞耳函数, 功率谱
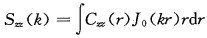
|
(3) |
式(2)和式(3)的离散形式分别为式(4)和式(5):
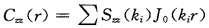
|
(4) |
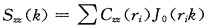
|
(5) |
拟合曲线在r=0时的值作为背景场误差方差Czz (0), 由OMB方差减去背景场误差方差得到观测误差方差。
为满足观测误差和背景场误差无偏性假设, 在求OMB协方差之前, 需分别从OMB中扣除各测站OMB平均偏差。
2 结果分析探空观测温度的误差主要是由温度探测仪敏感性(滞后)和太阳辐射造成的, 在500hPa以上较明显。底层温度背景场误差较大。较大背景场误差影响观测误差分析效果。我国探空仪一般上升高度在20hPa左右。因此只分析500~20hPa标准层。
2.1 温度OMB的平均偏差图 1显示:两个时次的共同特点是, 相同时次L波段、59型和美国区域探空仪温度观测OMB平均偏差变化趋势相似。在500hPa~250hPa之间都存在着较大OMB正平均偏差。峰值在300hPa附近, 在00时, 59型的约为0.6℃, L波段的为0.8℃; 在12时, 59型和L波段的基本一致, 都大约为0.5℃。这一垂直范围属于对流层, 温度递减率较大, 较大的正偏差主要原因可能是仪器探测温度滞后造成的, 背景场温度偏低也是原因之一。在200hPa~ 30hPa之间, OMB平均偏差较小, 一般为0.4~0.2℃之间。两个时次的主要差别是, 在00时, L波段的OMB平均偏差稍大于59型的, 在500~300hPa最明显, 约大0.2℃, 59型的更接近北美区域的。在12时则相反, 在500~200hPa, L波段和59型两者的OMB平均偏差基本一致, 其它层L波段的OMB平均偏差稍小于59型的。从数值上看, 无论哪种探空仪, 12时的OMB平均偏差明显小于00时的OMB平均偏差, 到高层更明显, 尤其是30hPa以上, 这种差别可达到1℃以上。这种差别主要可能是观测资料存在的日变化, 观测资料的辐射订正方案不够精确造成的。
|
图 1 温度观测OMB平均偏差 左:00时; 右:12时; 实线:59型; 虚线:L波段; 点线:北美 |
美国区域使用的探空仪主要是RS80型, 精度较好, 并常作为国际无线电探空仪比对的参照。如果忽视地区间背景场系统性误差的差异, 美国区域探空温度观测OMB平均偏差可作为一种比较的参照。从图 1中还可见, 在00时, 59型探空仪的OMB平均偏差更接近于美国区域OMB平均偏差; 而在12时则相反。
就总体而言, L波段和59型的OMB平均偏差差别不大, 一般都在0.2℃之内。这说明就与背景场的系统性偏差而言, 与59型探空仪温度资料相比, L波段探空仪温度资料没有明显的改进。
2.2 温度OMB的标准差我国L波段、59型和美国区域探空仪温度观测OMB标准差垂直廓线如图 2。

|
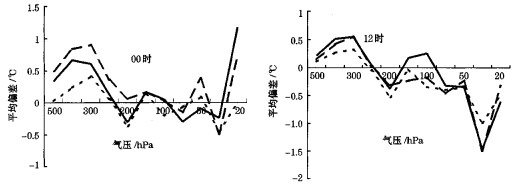
图 2 温度观测OMB标准差 左:00时; 右:12时; 实线:59型; 虚线:L波段; 点线:北美 |
无论00时还是12时, L波段、59型和美国区域的OMB标准差变化趋势也很相似:在500hPa~150hPa之间, 59型探空仪的温度观测OMB标准差从1℃上升到1. 70℃, L波段和美国区域的非常接近, 比59型的约小0.1~0.2℃。到100hPa以上, 它们的差距明显增大, L波段温度观测OMB标准差值介于59型和美国区域的之间, 比59型小0.2~0.4℃。
2.3 站点之间的对比分别选取4个距离在200km以内使用L波段探空仪和59型探空仪站点对。4对测站的位置如表 1。
|
|
表 1 使用L波段探空仪和59型探空仪距离较近的4对测站的位置 |
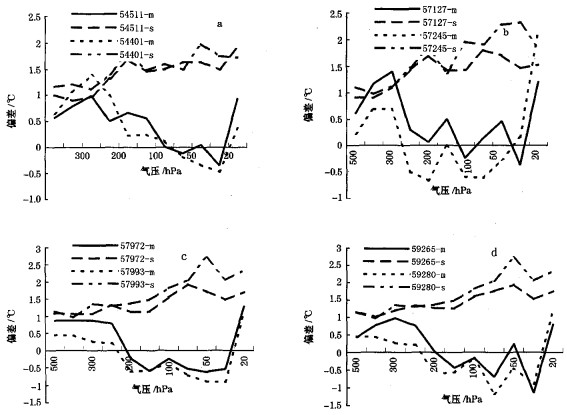
图 3为2005年3 -5月00时4个测站对的OMB平均偏差和垂直标准差。图中几乎所有59型的温度OMB平均偏差都稍微小于L波段的或基本相当, 而OMB标准差又都大于L波段的。这和图 2是一致的, 表明这两种探空仪所有站点综合比对分析和站点比对分析的结果是相符的。
|
图 3 4个站点对温度观测OMB平均偏差和标准差 右边方框中的数字为站点区站号; 'm'表示OMB平均偏差; 's'表示OMB标准差 |
L波段和59型探空仪温度资料OMB协方差曲线基本一致, 只存在一些因样本不同造成的微小差别, 不影响分析观测误差; 拟合的背景场误差协方差和统计的OMB协方差基本重合(图略), 说明贝塞尔函数拟合的精度比较高。图 4为L波段、59型、美国区域拟合的温度观测误差。
|
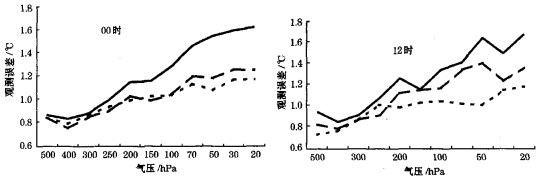
图 4 各标准层拟合的温度观测误差(℃) 实线:59型、虚线:L波段、点线:北美 |
如图 4, 在300 hPa以下, 两个时次L波段温度观测误差比59型的有所减小, 但不是很显著。但随着高度的增加, 差别越来越大。在00时, 59型、L波段温度观测误差差别尤其明显, 在50hPa以上L波段的比59型的减小达0.4℃以上。约为59型温度观测误差的四分之一, 而L波段的和美国区域的基本接近, 最大差别不到0.1℃。在12时, 在高层59型、L波段温度观测误差差别虽然不像00时这样明显, 但L波段温度观测误差也比59型的明显减小, 在50hPa以上减小达0.2~0.3℃。
3 结语分析结果表明, 相同时次L波段、59型和美国区域探空仪温度观测OMB平均偏差变化趋势相似。在500hPa~250hPa之间都存在着较大OMB正平均偏差。峰值在300hPa附近, 在00时, 59型的约为0.6℃, L波段的为0.8℃; 在12时, 59型和L波段的基本一致, 都大约为0.5℃。在200hPa~30hPa之间, OMB平均偏差较小, 一般为-0.4℃~0.2℃之间。两个时次的主要差别是, 在00时, L波段的OMB平均偏差稍大于59型的, 在500~300hPa最明显, 约大0.2℃, 59型的更接近北美区域的。在12时则相反, 在500~200hPa, L波段和59型两者的OMB平均偏差基本一致, 其它层L波段的OMB平均偏差稍小于59型的。这说明, 就与背景场的系统性偏差而言, 与59型探空仪温度资料相比, L波段探空仪温度资料没有明显的差别。
对于温度的OMB标准差和拟合观测误差, L波段有较大的改进。在300hPa层以下, L波段温度观测误差比59型的有所减小, 但不是很显著。但到高层, 差别越来越大, 在00时, 50hPa以上, L波段的比59型的可减少0.4℃以上。约占59型观测误差的四分之一。在12时, 在50hPa以上减小达0.2~0.3℃。
| [1] |
Huovila, S. Summary of WMO radiosonde intercomparisons. Radiosonde data quality and monitoring[R]. ECMWF/WMO workshop, 1987: 23-32.
|
| [2] |
Bottger, H. ECMWF monitoring system. Radiosonde data quality and monitoring[R]. ECMWF/WMO workshop, 1987: 181-190.
|
| [3] |
Xu Qin, Li Wei, Van Tuyl A., Barker E.H. Estimation of three-dimensional error covariance[J]. Part Ⅰ:Analysis of Height Innovation Vectors, Monthly Weather Review, 2001, 129(8): 2126-2135. |
| [4] |
陶士伟, 张跃堂, 陈卫红, 等. 全球观测资料质量监视评估[J]. 气象, 2006, 32(6): 53-58. DOI:10.7519/j.issn.1000-0526.2006.06.009 |
| [5] |
Gandin L.S. Complex quality control of meteorological observation[J]. MWR, 1988, 116(5): 1137-1156. |
 2006, Vol. 32
2006, Vol. 32 