2. 陕西省人工影响天气领导小组办公室
2. Meteorological Bureau of Shaanxi Province
利用雷达回波定量测量区域降雨, 国内外作了许多研究, 具有代表性的方法有Z-R关系法、平均校准法、卡尔曼滤波校准法、最优差值法、泰森多边形法等[1, 2], 这些方法基于雷达―雨量计联合测定区域降水, 误差一般不小于50 %。最常用的还是Z-R关系法, 它是利用Z =AIB确定A、B参数进行估算, 该计算公式单点取样的标准误差至少在±50 %, 估算降雨量时产生的误差更大[3]。随着计算机技术的发展, 我国大部分711雷达(包括新一代多普勒天气雷达)进行了数字化改造, 图像色彩分辨率采用每档5dBz, 反算的Z值误差在3倍左右, 远大于所需要的精度, 再者由于电磁波在降雨云层中衰减明显, 同一位置、不同类别的云层, 电磁波的衰减不同, 雷达回波的强度也不一样, 因此利用雷达回波强度估算降雨量的方法应用于实际时产生了非常大的误差。
但是雷达具有直观、探测范围大的特点, 因而进一步研究利用雷达回波的其他参数来估算降雨量的方法非常必要。通过对雷达资料进行细致的分类, 分析每类云层的回波特征[4], 得出降雨量的大小可能与云顶高度、15dBz高度、0 ℃层高度、0 ℃层厚度、0 ℃层回波强度、冷云高度、暖云厚度等因素有关, 通过降雨量与这些因素之间建立多元回归方程, 对降雨量进行估算并对误差进行分析, 是一种有益的尝试。
资料是利用2000 —2004年5年宝鸡711雷达观测的33天, 60个个例的稳定性层状云降雨回波, 见表 1。
|
|
表 1 2000至2004年稳定性层状云降雨个例季节分布 |
降雨的雷达回波按云层温度结构、空间延展和存在时间等可分为:冷云、暖云、对流云、层状云四大类[5]。冷云主要为降雪, 多出现在冬、春季节, 量级较小, 无与之配套的地面每小时降雪量; 暖云在宝鸡出现较少; 对流云结构复杂, 降雨时空分布更为复杂; 层状云降雨一般可分为混合性层状云和稳定性层状云, 混合性层状云之中有对流泡存在, 精确估算存在困难, 而稳定性层状云降雨, 融化层明显且融化层上下均无强回波区, 瞬间雨强变化不大, 降雨均匀, 云层结构简单, 寻找各种参数与降雨量之间的关系, 对于评估人工增雨效果有参考意义。
2 回波强度P与地面雨强I的关系宝鸡雷达站海拔高度630m, 距地面雨量观测站约150m。雨滴谱观测点在此下方约10m处。雨滴谱观测方法仍采用吸水纸色斑法, 读数面积S =28cm ×28cm, 取样时间间隔不等, 如2003年5月15日03 — 11时连续观测时段内, 在降水开始时, 每10分钟取一次样, 持续1小时。降水稳定后的第2、3小时, 每30分钟取一次样, 3小时后1小时取一次样, 直至降雨结束。为保证获取的雨滴粒子谱代表性和稳定性, 取样时要目测雨滴色斑不少于200个。计数处理时, 考虑了吸水纸的分辨率和减少溅散小滴影响[6 ~ 9], 最小雨滴尺度从0.0005m (500μm)起算计数, 直径间隔ΔD = 0.0002m (200 μm), 这样就获得了平均直径D为0.0006, 0.0008, …, (0.0006 +KΔD)的单位体积雨滴数浓度n (Di)
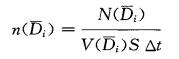
|
式中N(Di)为吸水纸上平均直径为Di的雨滴数(个), S为取样面积(28 ×28 × 10-4 m2), Δt是吸水纸承接雨滴的时间(秒), V(Di)是雨滴在静止大气中下降落速(m ·s-1)。为方便运算采用了两种落速表达式; Di < 0.001m时, V(Di) =9663×Di1.1e-230Di; 当Di>0.001m时, V(Di)= 4854 ×Di1.1e-196Di。与此对应的雨滴谱计算雨强:
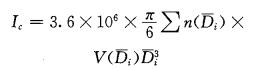
|
雷达反射率因子Z计算, 对于球型水滴, Z= ∑ni(Di)Di6。对于非球型、非均质(表面部分为水, 部分为冰)计算相当困难。文中假定在融化层中非球型冰相粒子基本融化成球型水粒子, 因而可近似用Z =∑ni(Di)Di6表示。考虑量纲, 因Di单位用米, 故Z =1018 ×∑n(Di)Di6。它和融化层雷达回波强度Pm有如下关系:Pm =10logZm, 即由Pm(dBz)可求得Zm = 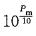
|
|
表 2 2003年5月15日回波强度反算与雨滴谱计算的Z值比较 |
|
|
表 3 回波强度及最大强度与雨强比较 |
从表 2、3分析表明:尽管711雷达经过了数字化改造升级, 但因设备老化, 又未经严格标定校准, 加之融化层粒子并未完全融化为球形水滴, 综合结果导致Pm值偏大, 与之对应的Zm明显高于Zc。但它们同总趋势仍相当好的呈现幂指数关系Z = AIB。如表 2, Zm、Zc与IR或Ic, 相关系数均高于0.967。表 2和表 3样本综合统计, 仍呈高相关, Z-IR和Z-Ic, 相关系数均高于0.93;B值接近, A值差异明显, 各为: Z =735.1I2.625R, Z =1112.1IC2.644。
2.2 IR与Ic的关系IR与Ic存在明显的相关关系。若以Ic =a +bIR形式回归表 2、3样本化, 相关系数R =0.948, a =0.2537, b =0.7514, b值和文献[7]全省4个测点有差异:一是云系不同部位; 二是由微观量向宏观量转化的不唯一性所致。尽管a、b取值不唯一, 但它们之间的显著相关, 为微观—宏观量耦合提供了可能。
3 稳定性层状云降雨量的估算 3.1 各种参数与降雨量的相关系数选取雷达回波参数的标准为[8, 9] :Pm, 融化层10km处回波强度; Pmax, 融化层回波最大强度; H, 云顶高度; H15, 云层衰减15dBz回波高度; H融厚, 融化层厚度; H零, 0 ℃层高度; H暖, 暖云厚度, 在零度层以下; H冷, 冷云厚度, 云顶高度H减H零高度。
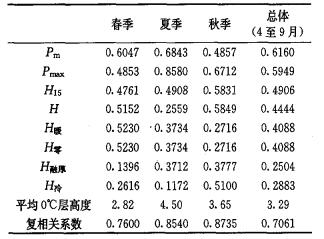
由表 4对60个稳定性层状云个例统计可以看出:
|
|
表 4 稳定性层状云降雨量与各种因子之间的相关系数 |
(1) 总体来说4 —9月, 稳定性层状云降雨量大小与上述8个因子均有正的相关关系。与雷达回波10km处零度层回波强度Pm关系最为密切, 达到0.616, 与回波最大强度, 相关系数达到0.5949;除此之外还与云层的高度(15dBz回波高度、云顶高度)关系密切, 相关系数分别为0.4906、0.4444;最后和暖云厚度和0 ℃层高度关系密切, 达到0.4088, 而与融化层厚度、冷云厚度关系不密切, 可见降雨是一个非常复杂的过程, 与云层的回波强度、云顶高度、零度层关系最为密切, 单一因子很难准确估算降雨量。
(2) 将雷达资料按季度求相关系数, 可见引起春季与夏季降雨的因子可能不同, 在春季降雨量的大小除与10 km处零度层回波强度关系密切外, 还和暖云厚度关系密切, 相关系数为0.523, 而秋季降雨量的大小与冷云厚度关系密切, 相关系数为0.51, 可能是春季近地层大气为冷向暖过度, 降雨量的大小主导因子为暖空气, 而秋季近地层大气由暖空气向冷空气转变, 降雨量的大小主导因子为冷空气。
(3) 在夏季, 稳定性层状云降雨量的大小与最大回波强度关系最为密切, 相关系数达到0.858, 其次为雷达回波10km处零度层回波强度相关系数达到0.6843, 最后为15dBz回波高度, 相关系数为0.4908, 暖云的厚度对降雨量的贡献较冷云厚度贡献大。
(4) 零度层高度对降雨的影响。春季零度层平均高度较低, 零度层高度与降雨量的相关系数较大, 为0.5230, 而秋季零度层高度与降雨量的相关系数不密切, 仅为0.2716。
(5) 各季节的复相关系数较高, 秋季复相关系数最高, 达0.8735, 最低的也达到0.76, 优于总体的相关系数。
3.2 误差分析利用回归方法建立的各季多元线性回归方程为:
春季

|
夏季

|
秋季

|
总体

|
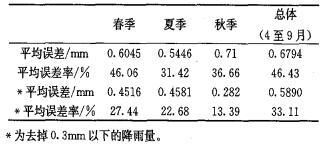
由表 5可知:
|
|
表 5 稳定性层状云降雨建立的多元回归方程平均误差 |
(1) 分季节建立的多元线性回归方程, 1h降雨量平均误差小于0.71mm, 夏季平均误差最小, 秋季平均误差最大。而平均误差率较大达到46.43 %, 夏季的平均误差率较小, 为31.42 %。
(2) 由于降雨量越小雨滴谱计算的降雨量与实际自计的雨量产生的误差越大, 去掉降雨量小于每小时0.3mm的个例, 利用多元线性回归方法建立的方程, 平均误差率为33.11 %, 平均误差和误差率有所降低, 按季节建立的回归方程效果较好, 最大误差率为27.44 %。
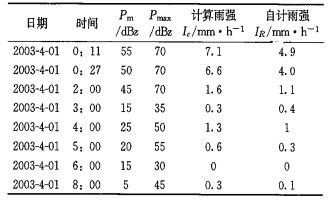
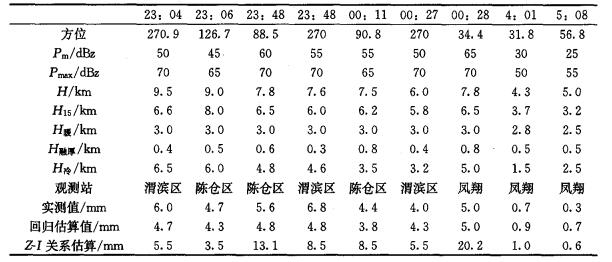
4 利用多元线性回归方程对降雨量的估算利用春季多元线性回归方程, 结合雷达回波对2003年3月31日—4月1日稳定性层状云降雨进行降雨量的估算。各雷达观测时次后1小时实测值之和为37.4m m, 估算值之和为33.3mm, 误差4.1mm, 平均误差率10.96 %, 降雨量越小相对误差越大, 见表 6。用Pm雷达回波强度反算Z, 用上述经验的Z-I关系估算降雨量时, 各个dBz值对应的雨强是确定的, 估算值之和为66.4mm, 误差29.0mm, 平均误差率77.54 %, 回波强度越大相对误差越大, 多元线性回归方法的优越性明显。
|
|
表 6 稳定性层状云2003年3月31日23时— 4月1日06时雷达观测各因子与降雨量的估算 |
(1) 由于数字化雷达探测的回波强度误差较大, 靠Z-I关系对降雨量估算产生较大的误差, 而多元回归方法考虑了回波强度、云顶高度、暖云厚度、零度层高度、融化层厚度等参数对降雨量的综合影响, 其物理意义更加明确。
(2) 稳定性层状云降雨, 利用多元线性回归方法建立的方程复相关系数较高, 估算降雨量优势明显, 准确率比使用Z-I关系估算降雨量有所提高, 业务运行是可行的。
| [1] |
张国君, 徐永胜, 贾绽云, 等. 湖南夏秋季雨滴谱的Z-I关系分析[J]. 气象, 2002, 28(增刊): 56-57. |
| [2] |
徐晶, 林建, 姚学祥, 等. 七大江河流域面雨量计算方法及应用[J]. 气象, 2001, 27(11): 13-16. |
| [3] |
梅森 B J. 云物理学[M]. 北京: 科学出版社, 1978: 502.
|
| [4] |
李金辉, 陈保国, 罗俊颉. 陕西关中层状云雷达回波特征[J]. 气象, 2004, 30(12): 53-56. |
| [5] |
李金辉, 陈保国, 罗俊颉. 陕西省中北部人工增雨适宜时段及层状云特征[J]. 气象科技, 2005, 33(1): 87-89. |
| [6] |
严采蘩, 陈万奎. 对流层下部雨滴谱分布[J]. 应用气象学报, 1990, 1(2): 191-198. |
| [7] |
严采蘩, 陈万奎. 国外雨滴谱分布函数的数值试验结果[J]. 气象, 1988, 19(9): 14-18. |
| [8] |
陈万奎, 严采蘩. 雨滴谱及其特征值水平分布的个例分析[J]. 气象, 1988, 14(1): 8-11. DOI:10.7519/j.issn.1000-0526.1988.01.002 |
| [9] |
罗俊颉, 樊鹏, 李金辉, 等. 陕西春季层状云降水雨滴谱部分特征[J]. 陕甘宁人工增雨技术开发研究, 2002, 123-127. |
 2006, Vol. 32
2006, Vol. 32