2. 兰州大学大气科学学院;
3. 山西省晋中市气象局
2. Atmospheric Science College of Lanzhou University;
3. Jinzhong Meteorological Office, Shanxi Province
准地转Q矢量(QG)理论是近代动力气象学的基础。中纬度大气的许多基本结构都可以使用准地转理论加以描述, 因此它是中纬度天气学, 或者说是中纬度地区天气预报的主要理论依据。从Hoskins1978年提出准地转垂直运动可由Q矢量散度来诊断以来, Q矢量在实际业务工作中不断被引申应用, 国内外许多专家、学者应用Q矢量诊断方法对不同的天气过程进行了诊断分析[1-10], 得出了一些有意义的结论。但准地转Q矢量受到准地转近似的限制, 不宜用于研究次天气尺度运动。张兴旺[11]由考虑了大气中水汽凝结非绝热作用的原始方程组出发, 推导出P坐标系的非地转的湿Q矢量Q*的表达式, 之后, 有人利用湿Q矢量对暴雨进行了一些诊断分析工作[12, 13], 但对Q矢量和湿Q矢量进行定量比较分析的还较少, 因此以发生在2001年7月26—27日山西省晋中市的一次区域性暴雨为例, 定量比较了准地转Q矢量和非地转湿Q矢量在暴雨诊断中的差异; 计算了湿Q矢量锋生函数(未曾发现有人进行过这项工作), 并与Q矢量锋生函数做了对比, 发现它们的分布和演变存在明显差异, 在对暴雨的落区和强度的诊断上, 湿Q矢量锋生函数更具优越性。
1 天气过程概述2001年7月23—29日, 晋中市出现强降水天气过程, 过程持续时间平均为4天, 过程降雨量最大132.9mm, 26日20时—27日20时日降雨量在51.1~90.2mm之间, 是晋中有降水记录以来唯一的一次全市11县(市)均达到暴雨标准的天气过程。从6小时降水分布图(图略)来看, 雨带基本呈东西向带状分布, 向偏东方向发展很快, 最强降水出现在26日夜间。
2 资料来源及处理为了确保计算、分析和比较的可靠性, 选取2001年7月25日20时—29日08时的20时和08时连续演变共8个时次、地面到300hPa共6层的实测资料, 资料范围为26~47°N、103~124°E。采用克里金方法对所选取的资料进行网格化插值, 形成插值格距为0.7°×0.7°, 网格数为31×31的网格化资料。各物理量计算中, 采用中央差分格式, 对于计算中用到的高度H, 温度T, u、v分量, 位温θ, 假相当位温θse均采用了其九点平滑值。另外, 在计算湿Q矢量时, 用到的垂直速度ω由运动学方法(积分连续方程法)计算求得, 为减小计算误差, 提高计算精度, 采用了二次修订方案进行修订。
3 Q矢量和湿Q矢量表达式 3.1 Q矢量表达式
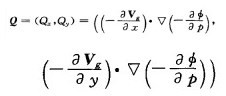
|
(1) |
这就是准地转Q矢量的表达式, 它还可以表示成如下分量形式:
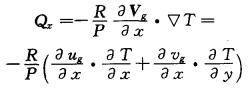
|
(2) |

|
(3) |
式中, 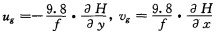
Q矢量散度:
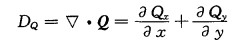
|
(4) |
锋生函数:
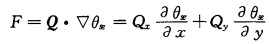
|
(5) |
在以上各项计算中, 均包含了地转风, 这就是准地转最明显的特征。
3.2 湿Q矢量(Q*)表达式由考虑了大气中水汽凝结非绝热作用的原始方程组出发, 可以推导出P坐标系的非地转的湿Q矢量, 其表达式为:
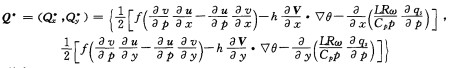
|
(6) |
其中,
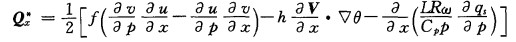
|
(7) |
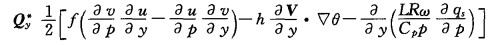
|
(8) |
在湿Q矢量表达式中, 不仅全部为实际风, 同时还包含了凝结潜热加热项, 这是与其它Q矢量明显不同的特征, 充分体现出其更接近实际大气的状况[2]。
4 准地转Q矢量和湿Q矢量的定量比较利用网格化资料, 根据公式(1)~(8)对7月25日20时—29日08时各层次的Q(湿Q)矢量、各分量场、Q(湿Q)矢量散度、Q(湿Q)矢量锋生函数分别进行了计算, 并做了Q(湿Q)矢量散度经纬向剖面图, 着重分析讨论850hPa、700hPa、500hPa和300hPa上上述各量的分布及演变特征。
4.1 Q(Q*)矢量、各分量与暴雨Qx、Qy分别为Q矢量在x、y方向上的分量。Qy表示温度梯度-∂T/∂y的大小变化, 当Qy>0时, 表示|-∂T/∂y|减小, 即锋消, 而当Qy < 0时, 表示|-∂T/∂y|增大, 即锋生。Qx则表示温度梯度-∂T/∂y的方向变化, 当Qx>0时, 表示-∇T作气旋式旋转, 而当Qx < 0时, 表示-∇T作反气旋式旋转。
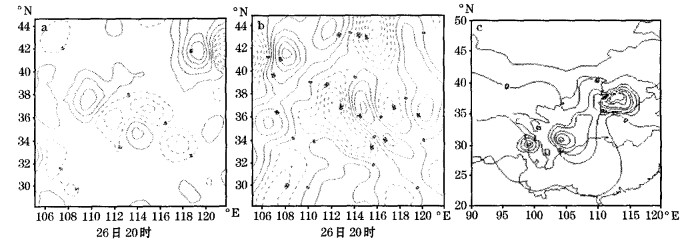
分析各层Qx和Qx*的时间演变, 就Qx而言:在反映锋区强弱能力上中低层明显优于高层, 降水前期700hPa比850hPa反映明显, 而当降水临近时, 850hPa比700hPa更好, 更具指示意义。在这种高、低空系统明显且配合较好的情况下, 高空300hPa上Qx的分布在某种程度上能反映地面系统的变化特征, 这对判断系统演变和降水的开始有着非常重要的意义, 而500hPa指示意义不明显。暴雨落区在Qx负值中心东南侧。与准地转Q矢量的Qx分布场相比, Qx*分布特征更为明显, 在反映各层系统变化和暴雨落区上都有良好的诊断特性, 在26日08时—28日20时的降水时段中, , Qx*的分布型式发生了明显的演变, 其负值区与降水区对应, 暴雨出现在等, Qx*线梯度最大且靠近负值区一侧, 负值最大中心数值较Qx负值中心明显偏大(图 1), 且Qx负值中心最大值较暴雨提前18小时出现, 而, Qx*负值中心最大值则提前6小时出现。由此也可看出, 二者对暴雨的预报都有一定的指示意义, 但Q矢量适宜于研究与天气尺度系统相关的大气运动, 而湿Q矢量更适宜于研图 1究天气尺度系统激发的次级环流。
|
图 1 2001年7月26日20时700hPaQx(a)和, Qx*(b)分布与27日02—08时雨量(c)对比 |
分析各层Qy和Qy*的时间演变, 可看出:Qy场是在强降水开始前6小时指示意义明显; 虽然降水区上空出现弱的辐散区, 但双侧强锋生作用相互促进, 使山西中部锋生作用迅速增强。在26日08时—28日08时的降水时段中, Qy*分布发生了较为明显的变化, 在暴雨发生的前6小时(26日20时), Qy*场有一个明显的突变, Qy*较Qy更能准确反映锋生作用的强弱, 且在与暴雨落区对应关系上更具优越性。
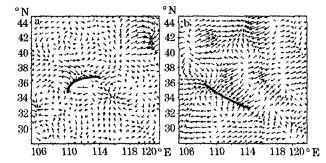
分析Q矢量图, 发现:700hPa表现最好, 其它层指示意义不明显。700hPa上(图 2), 26日20时, 河西走廊到山西西部出现一条带状分布的Q矢量的辐合线, 6小时后强降水出现在辐合线东南侧, 但辐合线分布的走向与降水轴线基本一致, Q矢量指向暴雨区。而Q*矢量图显示:500~850hPa均有明显反映, 辐合区与强降水带对应, 且其强度也较Q矢量的明显要强, 700hPa和850hPa上表现尤为突出。
|
图 2 2001年7月26日20时700hPa准地转Q矢量(a)和湿Q矢量(b)分布对比 粗实线代表辐合线 |
为了更好地揭示Q矢量与强降水的关系, 对Q矢量散度进行了计算、分析, 并分别选取暴雨区上空的112.8°E为基线作经向垂直剖面, 37.2°N为基线作纬向垂直剖面。
850~500hPa散度图上, 25日20时—26日08时(暴雨发生前12—24小时), 河套到山西一带均为南北或东北—西南走向的Q矢量散度辐合区所覆盖, 而东北和高原地区则为辐散区所覆盖, 演变趋势表现为与低层天气系统(低涡)相对应, 辐合带有明显的停滞或南北摆动的演变特点。暴雨发生在Q矢量散度辐合中心东南侧, 而不在辐合中心。并且, 锋区附近的Q矢量的辐合值较其南北两侧的都大。自西向东Q矢量的辐合和辐散区的分布呈非对称的耦合形式, 辐合和辐散区之中心间的距离为200km左右, 这与中尺度低涡的发展东移有关。
准地转Q矢量在四层的散度场分布对雨区有一定反映, 但在位置和强度上存在明显偏差, 而湿Q矢量散度场表现出良好的诊断特性, 对实际降水的反映明显优于准地转Q矢量, 其700hPa和850hPa散度辐合场能将主雨带与降水中心反映出来, 尤其是700hPa湿Q矢量散度辐合中心与降水中心一一对应, 二者不仅在位置上, 而且在强度上对应得也较好。500hPa和300hPa湿Q矢量散度辐合场对雨区的反映较准地转Q矢量也有不错的表现。从总体上看, 湿Q矢量的诊断特性比准地转Q矢量要好, 在暴雨出现前6小时表现得尤为突出。从总的预报效果来看, 700hPa湿Q矢量辐合中心对暴雨区预报有最好的指示意义。
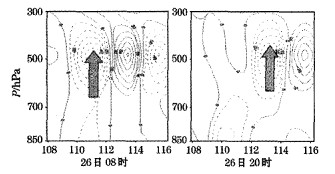
Q矢量散度在纬向上(图 3)呈耦合性对称分布, 随着降水的临近, 辐合中心在东移、加强, 辐合中心大约位于500hPa上, 湿Q矢量散度纬向分布与Q矢量散度有着类似的结构, 但其辐合中心位置偏低、强度偏强; 强降水开始前18小时, 其经向无明显辐合中心, 而在强降水开始前6小时, 出现强的辐合中心, 高度位于大约500hPa左右。湿Q矢量经向剖面图上(图略), 26日08时—27日20时在暴雨区上空一直存在较强辐合区, 辐合中心在650hPa左右, 位于35.8°N, 较最大降水中心的位置略偏南, 且湿Q矢量散度分布随高度略向北倾斜, 因而700hPa的散度辐合场与地面降水的位置有着较好的垂直对应。与Q矢量经向剖面图比较, 其辐合中心位置更接近实际强降水中心, 且强度明显大于Q矢量辐合中心, 更能反映实际降水强度。
|
图 3 2001年7月26日08时和20时准地转Q矢量散度纬向(沿37.2°N)垂直分布 |
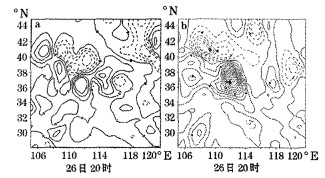
比较湿Q矢量锋生函数与Q矢量锋生函数(图 4), 发现它们之间存在明显差异:
|
图 4 2001年7月26日20时700hPa准地转Q矢量锋生函数(a)和湿Q矢量锋生函数(b)分布对比 |
(1) 在分布特征上:Q矢量锋生函数呈近似南北或东北—西南向的带状分布, 南北跨度8~10个纬距, 且其中有规律地分布着2~3个中心, 中心轴线位置与走向基本与地面锋面系统一致, 这是典型的准地转特征; 而湿Q矢量锋生函数分布则无此特征, 其强锋生中心只有一个, 南北跨度也较小, 只有4个纬距左右, 表现出明显的中尺度特征。
(2) 在反映雨区分布、强度、出现和维持时间上, 也存在明显不同:中低层Q矢量锋生函数基本能将强降水区反映出来, 但强降水区在强锋生轴线东南侧, 其强度反映上存在明显偏差, 出现时间上存在后延性, 850hPa比700hPa更具指示意义; 而湿Q矢量锋生函数则不同, 其锋生中心与降水区对应关系较好, 强锋生中心与暴雨区相对应, 在出现和维持时间上, 对应得也较好, 且各层均有不错的表现, 700hPa表现最佳。
综上所述, 湿Q矢量较准地转Q矢量更能反映出暴雨的落区和暴雨的中尺度特性, 在反映暴雨的强度上也更具优越性。
5 结语(1) 准地转Q矢量对暴雨的预报有一定的指示作用, 降水前期700hPa诊断效果最好, 但并不能完全将雨区反映出来, 且在暴雨的强度和落区上存在明显偏差, 而当降水临近时, 850hPa比700hPa更好; 300hPa上Qx的分布在某种程度上能反映地面系统的变化特征, 这对判断系统的演变和降水的开始有着非常重要的意义; 500hPa指示意义不明显。
(2) 湿Q矢量在各层对暴雨均表现出良好的诊断特性, 其散度辐合区与暴雨区有较好的对应关系, 其矢量指向暴雨区; 其强锋生出现6小时后开始产生强降水, 且强锋生中心与暴雨区有着较好的对应关系。利用湿Q矢量锋生函数可判断暴雨的强度、落区以及出现和维持时间, 700hPa表现尤为突出。
(3) 分析垂直剖面图得出:Q(湿Q)矢量散度在纬向上呈耦合性对称分布, 湿Q矢量散度辐合中心在650hPa左右, 其垂直对应暴雨区, 分布随高度略向北倾斜。
(4) Q矢量锋生函数分布表现出典型的准地转特征, 而湿Q矢量锋生函数分布则具有明显的中尺度特征。因此, Q矢量适宜于研究与天气尺度系统相关的大气运动, 而湿Q矢量更适宜于研究天气尺度系统激发的次级环流。湿Q矢量较准地转Q矢量更能反映出暴雨的落区和暴雨的中尺度特性, 在反映暴雨的强度上也更具优越性。
| [1] |
岳彩军. Q矢量及其在天气诊断分析中应用研究的进展[J]. 气象, 1999, 25(11): 3-8. |
| [2] |
杨晓霞, 谭志华, 华岩. 一次特大暴雨天气的Q*矢量分析[J]. 气象, 2001, 27(2): 44-47. DOI:10.7519/j.issn.1000-0526.2001.02.011 |
| [3] |
白乐生. 准地转Q矢量分析及其在短期天气预报中的应用[J]. 气象, 1988, 14(8): 25-30. DOI:10.7519/j.issn.1000-0526.1988.08.005 |
| [4] |
汪克付, 叶金印. 江淮梅雨锋暴雨过程Q矢量分析及落区预报[J]. 气象, 1995, 21(3): 40-43. DOI:10.7519/j.issn.1000-0526.1995.03.009 |
| [5] |
杨小燕, 曹希孝. 准地转Q矢量诊断场与暴雨关系的分析[J]. 气象, 1995, 21(11): 17-21. DOI:10.7519/j.issn.1000-0526.1995.11.004 |
| [6] |
Keyser D., M.J.Reader, R.J.Reed. A generalization of Petterssen's frontogenesis function and its relation to the forcing of vertical motion[J]. Mon. Wea. Rev., 1988, 116(3-4): 762-780. |
| [7] |
Lawrence B. Dumn.Evaluation of vertical motion: Past, Present, and Future[J]. Wea. Forecasting, 1991, 6(1): 65-73. DOI:10.1175/1520-0434(1991)006<0065:EOVMPP>2.0.CO;2 |
| [8] |
Hoskins.B.J., M.Pedder. The diagnosis of middle latitude synoptic development[J]. Quart. J. Roy. Meteor. Soc., 1980, 106(450): 707-719. DOI:10.1002/(ISSN)1477-870X |
| [9] |
车锡果, 刘庆军, 沈跃琴, 等. 准地转Q矢量分析方法在宁夏夏季降水天气预报中的应用[J]. 高原气象, 1995, 14(2): 192-197. |
| [10] |
郁淑华, 骆红. 川东北涡暴雨环境场及Q矢量分析[J]. 高原气象, 1991, 10(1): 70-76. |
| [11] |
张兴旺. 修改的Q矢量表达式及其应用[J]. 热带气象学报, 1999, 15(2): 162-167. |
| [12] |
姚秀萍, 于玉斌. 非地转湿Q矢量及其在华北特大台风暴雨中的应用[J]. 气象学报, 2000, 58(4): 436-446. DOI:10.11676/qxxb2000.046 |
| [13] |
王川, 杜川利, 寿绍文. Q矢量理论在青藏高原东侧大暴雨过程中的诊断应用[J]. 高原气象, 2005, 24(2): 261-267. |
| [14] |
岳彩军, 寿绍文. 定量分析几种Q矢量[J]. 应用气象学报, 2003, 14(1): 40-47. |
 2006, Vol. 32
2006, Vol. 32