2. 黄淮学院数学系
2. Mathematic Department, Huanghuai University
旬降水量分级是旬天气预报的基础,因此对旬降水量等级合理的划分是非常重要的,它直接影响到气象预报的准确性和服务效果。
日降水量的分级是根据预报业务需要对实时降水量的分级[1],表现为具体数量。而旬降水量的分级则是建立在降水气候态基础收稿日期:2007年1月23日;修定稿日期:2007年9月10日上,其与干旱、洪涝等级等一样都是基于气候态的相对量。邹旭恺等[2]指出, 目前有3类常用的建立基于降水气候态的干旱指标的方法:一是降水距平百分率指标,如RAI[3]和BMDI[4];二是降水量分位数法,如澳大利亚的十分位De ciles指数[5];三是假定降水量符合某种概率分布函数,然后做标准化变换得到的指数,如SPI指数[6]。旬降水量的分级则与其相似。前两种方法虽简单,但实际上暗含降水量为正态分布的前提,而月尺度以下的降水大多不服从正态分布,而是近于Г分布[7]。第3种方法划分效果较好,但相对复杂,因为降水量分布函数的区域性、季节性变化比较大,以吉林省为例,西部的白城、松原地区与东部的吉林、通化的降水量差异明显,而同一地区夏季降雨与冬季降雪无论在降水量级还是年际变率上差异都比较明显。因此对旬降水量等级合理的、实用的划分办法既要考虑其自身概率分布,又要避免大量的分布函数参数计算。
在国内,各地方都根据自身的降水特点采用相应的划分标准和办法,这些划分办法的优劣性和合理性也各不同。吉林省现行的旬降水量分级办法是1980年代提出的,沿用至今。本文将在讨论该方法合理性的基础上,给出基于降水概率分布函数的客观划分办法,并力图使该方法具有一定的普适性。
1 资料和方法 1.1 资料本文应用的资料是由1961—2000年吉林省50站逐日降水资料计算而得的全省以及省内9个地区的40年旬平均降水资料。
1.2 正态分布检验方法在众多正态性检验方法中,“偏度、峰度检验法”和“夏皮罗—威尔克法”较为有效[8],本文采用第一种方法。
对某旬平均降水量(或其Z指数)序列进行正态分布检验,首先计算该序列的偏态系数(γ1)和峰态系数(γ2)。若样本为正态分布,近似有
| $ {\gamma _1} \sim N\left( {0, {\sigma _1}} \right), \gamma \sim N\left( {{\mu _{2, }}{\sigma _2}} \right) $ | (1) |
而后构造如下统计量:
| $ {u_1} = {\gamma _1}/{\sigma _1}, {u_2} = \left( {{\gamma _2} - {\mu _2}} \right)/{\sigma _2} $ | (2) |
式中,
其中n为该序列的样本总数。这里将|u1|、|u2|同时小于1.96(α =0.05)的序列定义为正态分布序列,将|u1|、|u2|只有一个小于1.96,另一个值小于3.3(α=0.001)的序列定义为准正态分布序列,其他序列为偏态序列。
2 吉林省气象台现行旬平均降水资料分级标准吉林省气象台现行的旬降水量分级标准以及划分方法如下:(1)正常值为气候均值;(2)在大于气候均值的年份中,将要素值从大到小排序,按概率依次取20%的年份为特多年,40%的年份为偏多年,40%的年份为稍多年;(3)在小于气候均值的年份中,将要素值从小到大排序,按概率依次取20%的年份为特少年,40%的年份为偏少年,40%的年份为稍少年;(4)临界值取相邻年份要素的插值。
可以看出,该标准是降水量分位数法的一种,用降水量大小年份的概率分布代替了降水量本身的概率分布来对降水进行等级划分。可以知道,对于正态分布的要素时间序列,该标准对应的降水量分布与降水量自身的分布是基本相符合的,但对于偏态分布的序列来说,两者之间就会出现较大的差异。以吉林省西部地区冬季降水为例,该区旬降水量普遍偏少,但变率较大(某些年份存在很大极值),这就使得绝大多数年份降水量均小于要素气候均值(即气候均值对应的降水量是相对的小概率事件),而从统计角度正常值大多为概率分布的最大值,因此以要素气候均值作为正常值的做法就有待商榷。同时通过插值获得的临界值具有随机性,误差较大。
为此,首先对1961—2000年吉林省及其9个地区全年36个旬的旬降水(R)序列进行了正态分布检验,来分析现行标准的适用性。表 1给出了检验结果,其中第一行的整数为36旬中相应分布序列的个数,第二行括号中百分数为其对应的百分率。
|
|
表 1 吉林省及其9个地区全年36个旬的旬降水(R)序列正态分布检验结果 |
由表 1可以看到,无论是全省还是各地区旬降水资料的正态分布率都很低,全省降水有1 5个旬成正态分布,另有7个旬为准正态分布,在9个地区中中东部地区正态率要高于西部地区,吉林地区正态率最高(有10旬),白城地区最低(仅3旬)。另外正态分布的降水序列大多出现在夏季。因此,从旬降水量分布函数来看,现行标准适用性不够广泛,特别是针对每一地区的划分结果,更不容易真正反映实际降水的等级。因此需要寻找更为客观化的,基于降水量本身分布函数性质的一个分级办法。
3 客观分级的方法及其标准偏态序列的直接划分存在一定的不确定性,首先偏态序列的分布函数具有不确定性,因此分布函数的检验和参数初始化较复杂。一般来说,通过概率分布函数合理确定降水量等级的前提是样本正态分布,而实际的降水量,特别是月以下时间尺度的降水大多近于Г分布。为了获得标准化正态分布,引入如下的Z指数[9]转换。
对于逐年各旬降水量时间序列R,先计算其标准化距平
| $ Z\left( k \right) = \frac{6}{{{c_s}}}{\left( {\frac{{{c_s}}}{2}\widetilde R\left( k \right) + 1} \right)^{1/3}} - \frac{6}{{{c_s}}} + \frac{{{c_s}}}{6} $ | (3) |
式中,k=1,40为年份,cs为偏态系数,σ为均方差。
对各地区旬降水序列的Z指数进行了正态分布检验(见表 2,说明同表 1),发现Z指数序列具有很好的正态性。全省36旬中只有两旬为显著偏态,显著正态率达80.6%,在9个地区中,显著正态率最高的是白山地区,达90%以上,最低的白城地区也有13旬显著正态分布,11旬准正态分布,较原序列的正态性有显著提高。值得注意的是偏态分布的Z指数序列其计算所得的|u1|、|u2|值较原降水序列计算结果小一个量级。因此,应用降水资料的Z指数序列分布函数作为基础来进行分级更为合理。
|
|
表 2 吉林省及其9个地区全年36个旬Z指数序列的正态分布检验结果 |
这里,根据吉林省现行旬降水量等级划分标准中,给出应用Z指数划分降水多寡的划分标准(见表 3)。根据这一标准,通过公式(3)反算即可得相应的降水序列的等级划分结果。
|
|
表 3 Z指数等级划分标准 |
应用上述客观划分办法,对全省及9个区域的旬降水量进行等级划分。这里按对应的R序列和Z序列的正态分布性选取有代表性的旬个例,给出全省旬降水量的划分结果。作为比较,同时也给出了现行划分标准和办法下的结果。
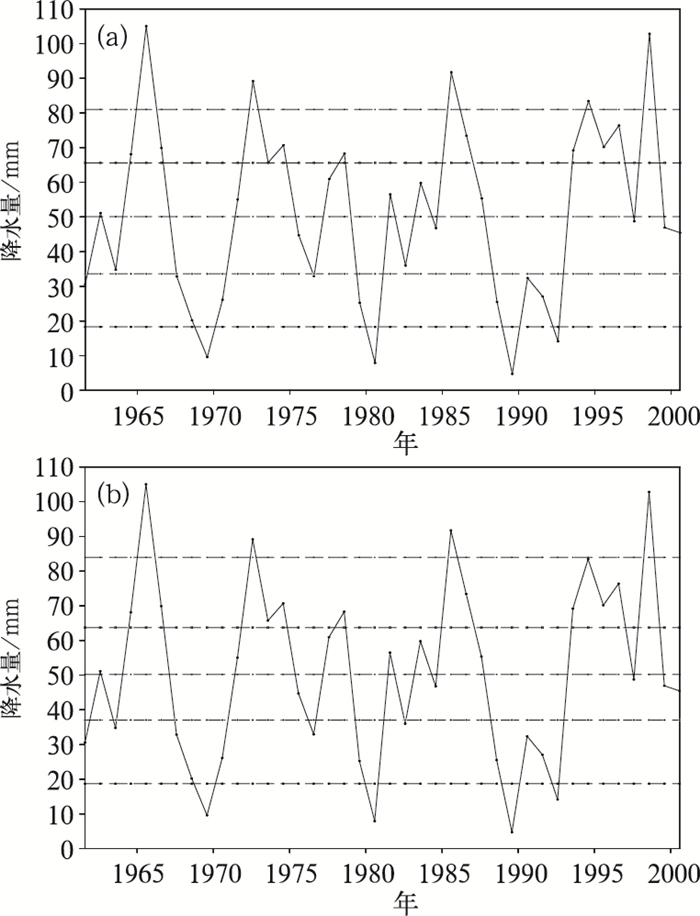
4.1 R正态Z正态的序列在36旬中,共有15旬的全省旬降水序列为R正态Z正态序列,这里以8月上旬为例(图 1)。正如前面讨论的,对于R正态Z正态序列,新标准与现行标准的划分结果比较相近。但新标准的划分更符合概率分布的特点,即气候均值附近为高概率区域,越向两侧,概率越低,因此偏多(低)较稍多(低)等级内的降水量级跨度要小。同时分析这15旬,发现,新标准的划分结果相对稳定,而现行标准的划分结果受实际序列的变化影响较大,具有一定的随机性。
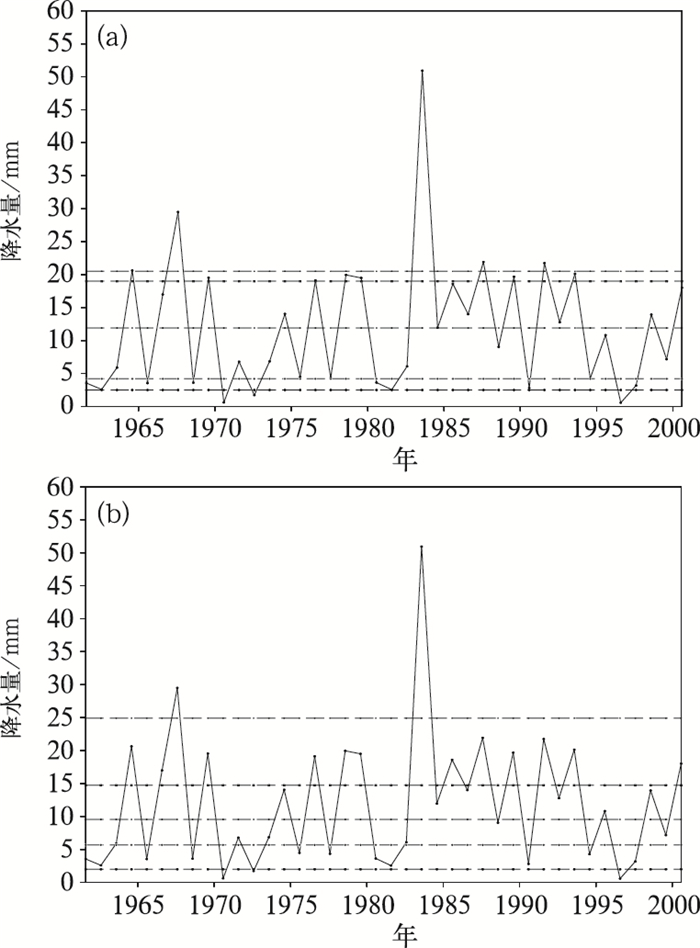
4.2 R偏态Z正态的序列在36旬中,共有9旬的全省旬降水序列为R偏态Z正态序列,这里以4月下旬为例(图 2)。图中可以明显看出,新标准的划分更为合理,因为对于偏态降水序列,大值降水为相对的小概率事件,因此降水量等级越高其跨度越大。如果等级划分是根据年份的概率而得,所以对于当多年的降水量相对集中于某一值时,就必然会出现类似图 2a中偏多等级降水量跨度很小的情况,而客观分析办法不会出现类似问题。
|
图 1 8月上旬全省旬降水量等级划分结果 图中虚线分割开的6个等级自上而下分别为特多、偏多、稍多、稍少、偏少、特少;虚线表示各等级间的临界值a.现行标准划分,b.客观标准划分 |
|
图 2 4月下旬全省旬降水量等级划分结果 说明同图 1 |
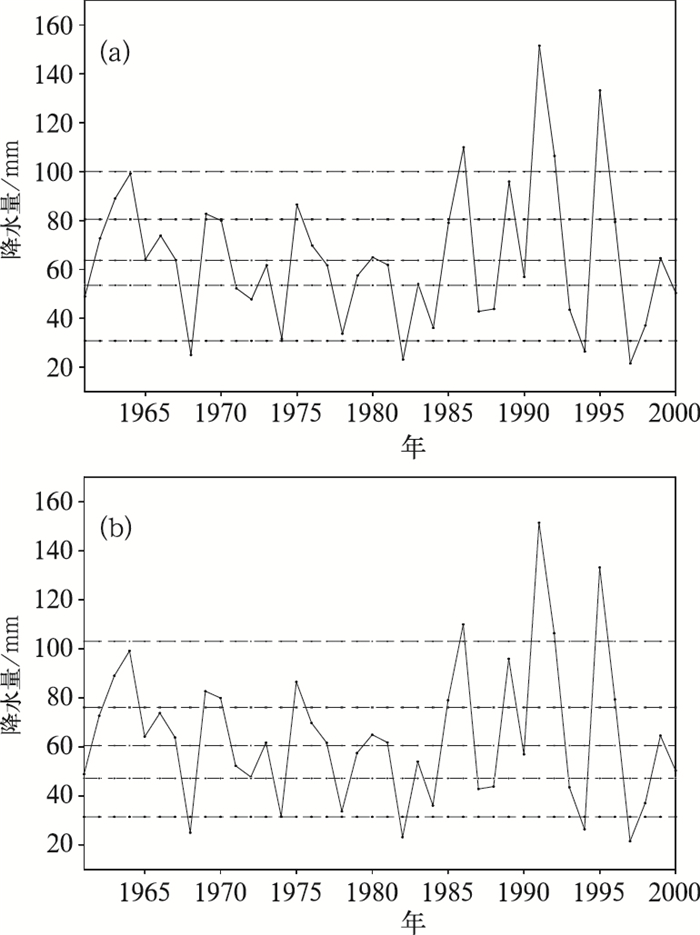
在36旬中,共有5旬的全省旬降水序列为R准正态Z正态序列,这里以7月下旬为例(图 3)。对于这样的R准正态Z正态序列,其划分结果的差异同样比较小,图 3中,两种办法划分的稍少量级差异较大,其主要原因还是因为现行办法是基于发生年份概率而得,而客观办法由降水的概率分布而得,另现行标准中临界值的插值也是不可忽视的原因。
|
图 3 7月下旬全省旬降水量等级划分结果 说明同图 1 |
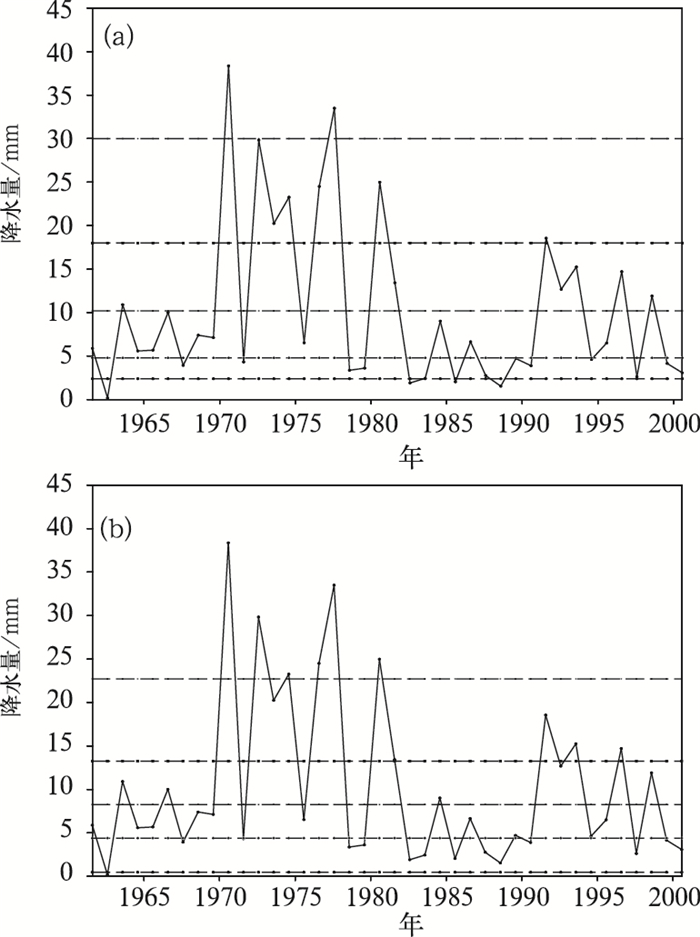
在36旬中,共有3旬的全省旬降水序列为R偏态Z准正态序列,这里以10月下旬为例(图 4)。比较图 2发现,对于R偏态的序列,尽管Z序列的分布函数正态性有偏差,但客观划分的结果(图 4b与图 2b)其特点有一致性,而现行标准划分的结果(图 4a与图 2a)差异较大,进一步说明了现行标准划分降水等级的不稳定性。
|
图 4 10月下旬全省旬降水量等级划分结果 说明同图 1 |
本文根据吉林省现行的基于降水量大小年份的概率分布的旬降水量等级划分标准和办法,提出了一种客观划分办法。该方法基于降水概率分布函数,考虑到旬降水量本身的偏态性,引入Z指数变化,通过对Z指数的划分反算而得实际降水量的划分结果。将本文的客观标准与现行标准的划分结果进行比较分析,发现客观标准的划分结果稳定,随机性小,结果更为合理。由于该方法既考虑其自身概率分布,又避免复杂的分布函数参数计算,因此新方法更具有普适性。这一方法仍需进一步完善,比如对于降水偏少的单站或区域,其降水量的分布近于指数分布,通过Z指数变化虽一定程度上改善了其偏态性,但其划分结果仍可能缺乏合理性,需要结合其他办法进行订正。
| [1] |
张学文, 尹道声. 用等级表示降水量的大小[J]. 气象, 1989, 15(12): 34-36, 43. DOI:10.7519/j.issn.1000-0526.1989.12.009 |
| [2] |
邹旭恺, 张强, 王有民, 等. 干旱指标研究进展及中美两国国家级干旱监测[J]. 气象, 2005, 31(7): 6-9. DOI:10.7519/j.issn.1000-0526.2005.07.002 |
| [3] |
Van-Rooy M. P.. A Rainfall anomaly index (RAI) independent of ti me and space[J]. Notos, 1965(14): 43. |
| [4] |
Bhalme H.N, Mooley D.A. Large-scale drought/floods and monsoon circulation[J]. Mon.Wea.Rev, 1980, 108: 1197-1211. DOI:10.1175/1520-0493(1980)108<1197:LSDAMC>2.0.CO;2 |
| [5] |
Gibbs, W. J. and J. V. Maher. Rainfall deciles as drought indicators[R]. Bureau of Meteorology Bulletin, Commonwealth of Australia, Melbourne, 1967: 48.
|
| [6] |
Mckee, T. B., N. J. Doesken and J. Kleist. The relationship of drought fr equency and duration to time scales[M]. Preprints, Eighth Conf. on Applied Climatology, Anheim, CA, Amer. Meteor. Soc., 1993: 179-184.
|
| [7] |
么枕生. 气候统计学基础[M]. 北京: 科学出版社, 1984: 101-108.
|
| [8] |
盛骤, 谢式千, 潘承毅. 概率论与数理统计(第2版)[M]. 北京: 高等教育出版社, 1995: 222-225.
|
| [9] |
高波, 陈乾金, 任殿东. 江南南部-华南北部前汛期严重旱涝诊断分析[J]. 应用气象学报, 1999, 10(2): 219-226. |
 2007, Vol. 33
2007, Vol. 33