2. 中国气象局上海台风研究所
2. Shanghai Typhoon Institute, CMA
近年来热带气旋数值预报模式发展迅速,路径数值预报的精度不断提高,其中较为先进的有GFDL(美国海洋大气局地球流体动力实验室有限区域数值预报模式)、NOGAPS(美国海军全球大气预报谱模式)、UKMET(英国气象局全球谱模式),以及日本气象厅的有限区域谱模式TYM等。2005年GFDL大西洋飓风预报的24、48和72小时误差分别为97.1、162.8和252.9km,上面提到的其它模式也稳定在24小时120km、48小时200km和72小时300km左右[1-2]。而我国在台风数值预报模式研制和应用方起步比较晚,目前国家气象中心、上海台风研究所和广州热带海洋气象研究所都建立了台风模式并投入到业务使用。国家气象中心的台风模式为全球谱模式(T213L31),用最优差值法进行客观分析,在分析场中加入非对称人造台风,对西太平洋和中国南海区域的台风每天进行4次120小时预报。该模式的预报能力已接近中央气象台的主观预报, 有时甚至还好于主观预报, 特别是48小时以上时效的客观模式较主观预报具有一定的优势[3]。上海台风研究所的台风模式是基于MM5发展起来的[4],采用Bogus技术,对进入18°N以北、156°E以西的台风进行一天二次的72小时路径预报。而广州区域气象中心的台风数值预报模式是在热带有限区业务模式(TC10)基础上发展起来的[5],用最优插值法进行客观分析,通过加入人造台风方法得到初始场,对进入15°N以北、125°E以西的台风进行一天二次的48小时预报。2005年各家数值模式的平均距离误差24小时为154.0km,48小时为279.2km[2]。
中国气象局气象数值预报创新基地开发了多尺度的同化与数值预报系统(简称GRAPES, Global Regional Assimilation and Prediction System)[6]。该系统采用全可压原始方程组,集常规与非常规变分同化、静力平衡与非静力平衡、全球与区域模式、科研与业务应用、串行与并行计算、标准化与模块化程序、理想试验与实际预报为一体,中小尺度与大尺度通用的数值预报系统[7]。现有的结果表明,GRAPES对天气形势和中尺度天气系统有较好的预报能力[8]。基于GRAPES的GRAPES_TCM[9]于2004年6月开始准业务预报试验。经过准业务试验和实际运行的结果看,它对热带气旋路径具有良好的预报精度和预报稳定性。
自GRAPES_TCM建立以来,GRAPES已进行了数次升级,涉及完善动力框架程序,添加新的物理过程等。其版本已由GRAPES 2.1更新为GRAPES 2.6。因此,需要将GRAPES_TCM的内核更新为GRAPES 2.6,并检验新版本模式对于热带气旋路径的预报性能。本文通过大样本检验,分析GRAPES_TCM 2.6(以下简称GT2.6)72小时内的路径预报性能,并与GRAPES _TCM 2.1(以下简称GT2.1)进行比较。
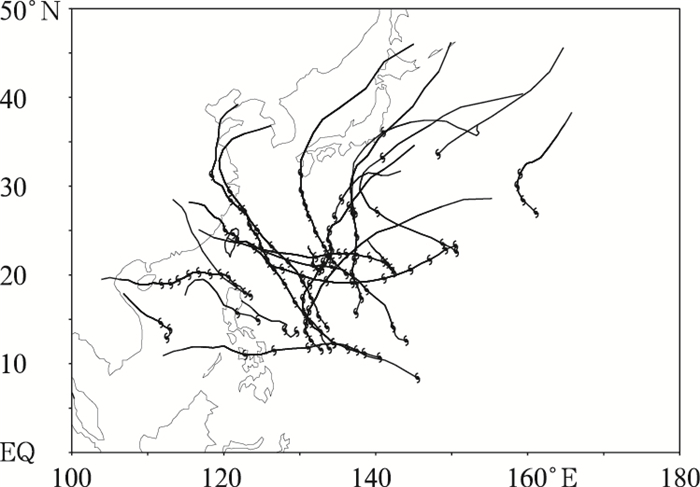
1 资料和方法 1.1 资料2005年GT2.1共进行了195次48小时准业务预报,受现有资料限制,本试验从中选取了20个热带气旋的共126个预报样本(见表 1),占总样本数的64.6%。其中维持时间达到72小时的有97个,占所有维持时间达到72小时样本的68.7%。本文使用的路径实际资料来自《西太平洋热带气旋年鉴》的最佳路径,图 1为所选样本的路径图。可以看出,所有路径呈现出西或西北行和转向(均为向东北转向)两种形态。绝大部分样本位于30°N以南、150°E以西,130°E以东多出现转向路径,以西则多为西或西北行路径。本文将GT2.6的模拟时长设定为72小时,对生命史短于72小时的样本只作48小时模拟。与GT2.1一样,GT2.6的样本模拟均采用AVN资料和涡旋重定位方案构建初始场,侧边界每12小时更新一次。GT2.6的基本属性和参数化设置与GT2.1相同,参看文献[9]。
|
|
表 1 模拟的热带气旋及样本数统计 |
|
图 1 所有样本的最佳路径 台风标志为起报位置 |
本文主要分析GT2.6的平均距离误差、系统偏差、距离误差的地理分布和平均移速误差。距离误差的定义为模拟路径位置与最佳路径位置间的大圆弧长[10]。除了对总体样本检验外,本文还将所有样本进行分类检验,包括路径类型、强度大小、有无登陆过程以及有无移向或移速突变。
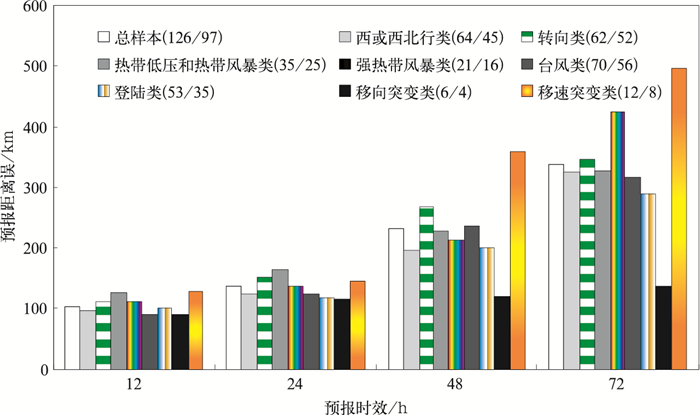
2 GT2.6路径预报性能检验 2.1 平均距离误差总体平均:图 2为GT2.6对所有热带气旋路径预报的样本和分类样本的距离误差比较。从图 2看出,GT2.6预报的24、48和72小时的总体平均误差分别为135.8、230.7和336.0km。由式(1)可得GT2.6的预报技巧[11],其中P为预报技巧,EC和EG分别为CLIPER[12]和GT2.6的平均距离误差。所有试验样本中CLIPER预报的有76个(预报时效均达72小时),基于它们算得GT2.6在24、48和72小时的预报技巧分别为24.9%、38.7%和47.4%。可见GT2.6的预报技巧随预报时间的增加而提高,其对热带气旋路径的预报特别是72小时的预报有很好的效果。值得注意的是,GT2.6在12小时的预报平均误差较大,接近100km,这可能是由于模式预报的初期受模式初始场影响较大[10],由此看出,GT2.6使用的初始化方案还需进一步改进。
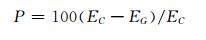
|
(1) |
|
图 2 GT2.6总样本和分类样本的距离误差 括号里为预报时效达48/72小时的样本数 |
按热带气旋路径形态分类:据图 1,所用预报样本的路径可分为西或西北行和转向这两种类型。图 2显示,西或西北行类样本的路径距离误差在24、48和72小时分别比总体平均小13.8、35.8和13.4km,而转向类样本则相反,其距离误差在24、48和72小时分别比总体平均大14.3、36.9和11.6km。这说明GT2.6对西或西北行类样本的预报性能要优于对转向类样本的,这种优势在48小时尤其显著(72.7km)。
按热带气旋强度分类:根据预报时刻热带气旋强度(近中心最大风速用Vmax表示)可将所有样本分为3种类型[9]:热带风暴和热带低压(Vmax<24.4m·s-1),强热带风暴(24.4m·s-1≤Vmax<32.6m·s-1)和台风(Vmax≥32.6m·s-1)。热带气旋强度达台风的样本最多,占总数的55.6%;热带风暴和热带低压类次之,占总数的27.7%;强热带风暴类最少,只占总数的16.7%(图 2)。在12和24小时,热带低压和热带风暴类平均误差比强热带风暴类大14和27km,强热带风暴类平均误差又比台风类大20和13km。由此可见,在前24小时,这三类的误差随着强度的增大而减小。然而,在48和72小时却不存在这样的关系,在48小时台风类最大,而在72小时强热带风暴类的距离误差比其它两类大近100km。这里分析的结果与文献[9]的结果不尽一致,文献[9]对于不同强度热带气旋路径预报有一定的规律性,但是那种规律性在2005年预报中表现得并不明显,这可能与模式的初始场以及GRAPES_TCM还不具备模拟热带气旋强度能力有关。
登陆热带气旋样本:本文定义的登陆样本是指在模拟时间内最佳路径中有登陆过程的样本。该类样本在24、48和72小时的距离误差为117.7、200.1和287.8km,分别比总体平均小了18.1、30.6和48.2km(图 2)。这说明GT2.6对登陆热带气旋的路径预报具有较高的参考价值。该类样本模拟比较好的可能原因是由于它靠近陆地,观测资料比较多,使得模式可以更准确地描述大尺度环流和涡旋环流[13],因此便容易得到较准确的路径预报。
热带气旋路径移向和移速突变类:移向突变是指热带气旋前后12小时平均移向角度差左折≥30°或者右折≥45°[14]。而移速突变是指热带气旋前后12小时移速变化绝对值≥15km·h-1,若风速初速≤5km·h-1,则前后12小时移速增加10km·h-1或以上也为移速突增[15]。图 2显示,移向突变类的距离误差在72小时内都明显小于总体平均,其48和72小时的距离误差均不超过140km。移速突变类则相反,12小时的距离误差比总体平均大24.0km,达到127.0km,48和72小时更是大了127.4和160.2km,达到358.1和496.2km。以上说明GT2.6对移向突变类样本有一定的预报能力,而对移速突变类的路径相对较差些。但是,由于这两类样本数目较少(10个左右),上述结论有待以后用更多样本进行验证。
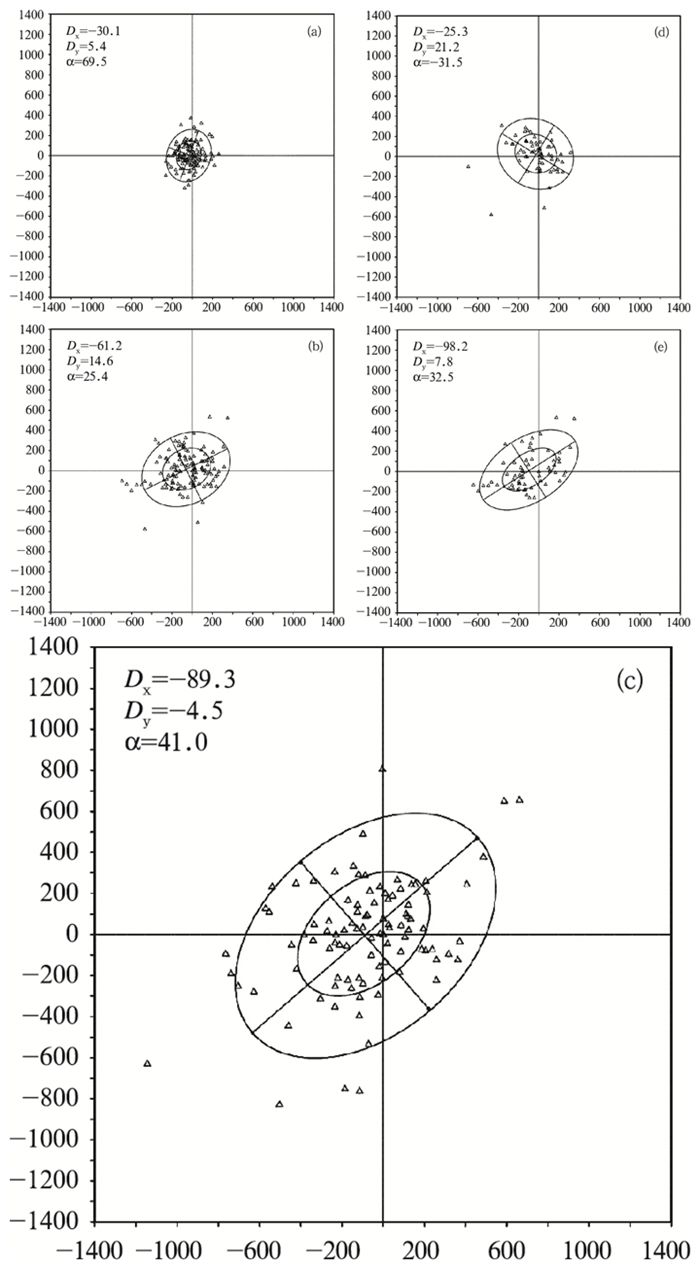
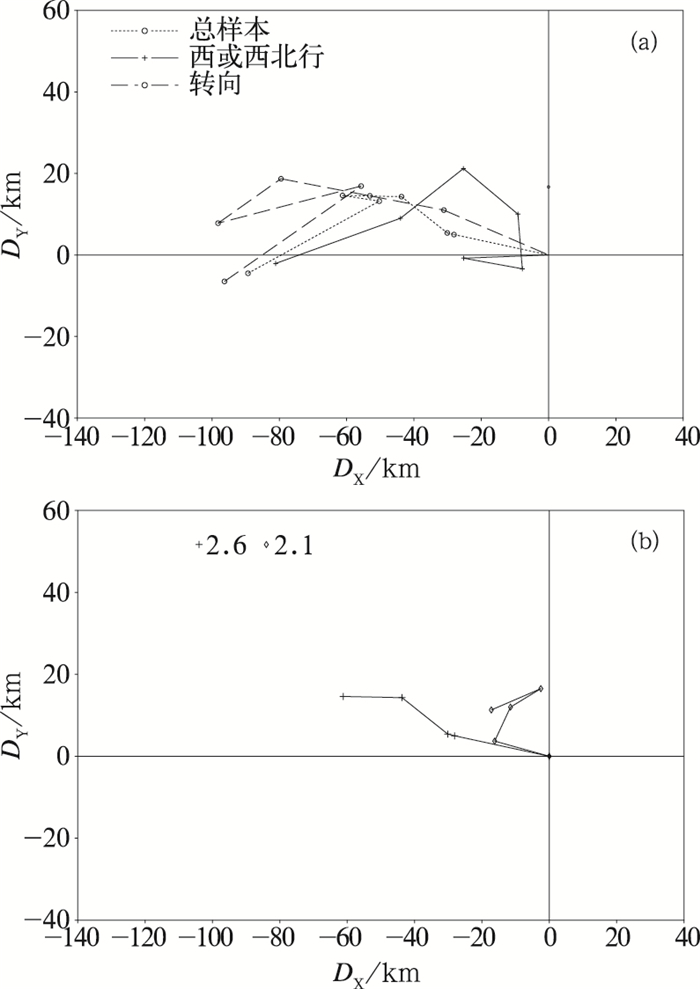
2.2 系统性偏差为了考察GT2.6对路径的预报是否存在系统性的偏差,对每个样本计算其预报位置相对于最佳路径位置的经向和纬向距离。用这些距离绘成的散点图即为预报位置相对最佳路径位置(原点)的分布图,然后在二元正态概率分布假设下,计算理论上包含50%和90%散点的概率椭圆[16](图 3)。由图 3可以看出,GT2.6的概率椭圆在72小时内都是东北-西南向,这种分布型在24小时后表现更加突出。这意味着偏离较远的预报位置多位于观测位置的东北或西南侧,分别对应于对转向(通常向东北)的高估和低估[11]。不同路径类型的偏差分布也显示(见图 3),东北-西南向的误差主要来源于对转向样本的预报。这说明GT2.6的总体平均误差主要来源于对转向的预报。这与之前的分类比较结果一致。GT2.6的概率椭圆随预报时间的增长而面积变大,这是因为模式的预报误差随预报时间增长而增大。由图 4a可以看出,GT2.6对所有样本、西或西北行类和转向类都有向西(稍偏北)的系统偏差。前48小时,所有样本和转向类的偏差随预报时间向西增大,48小时后有所振荡,而西或西北行类的偏差在前24小时先增后减,之后持续增大,三类样本的72小时偏差都达到90km左右。这说明GT2.6的预报位置倾向于偏向最佳路径位置的西侧,且这种趋势大体上随预报时间的增长而变大。这与散点图反映的趋势是一致的。对于西或西北行样本,这意味着GT2.6的预报路径比最佳路径偏快。而对于转向样本则意味着GT2.6倾向于低估转向[13]。用系统偏差订正上述三类样本的预报路径发现,所有样本、西或西北行类的距离误差在大部分时次有小幅减小;而转向类则取得了较大的改进,18~48小时改进超过了10km,误差缩小达5%以上,这是因为转向类样本偏差分布的一致性较其它两个样本更强(图 3b、d、e)。建议业务应用中在参考GT2.6的路径预报时(特别是对转向类样本的24~48小时预报)考虑消去图 4a所示的系统偏差。
|
图 3 GT2.6样本偏差分布 a、b、c分别为总样本24、48、72小时偏差;d、e分别为西或西北行类和转向类48小时偏差分布;DX和DY分别为纬向和经向平均偏差;α为坐标横轴与椭圆长轴组成的最小夹角;大小椭圆分别包含90%和50%的散点 |
|
图 4 GT2.6的系统偏差(a)及48小时内GT2.6和GT2.1的系统偏差对比(b) |
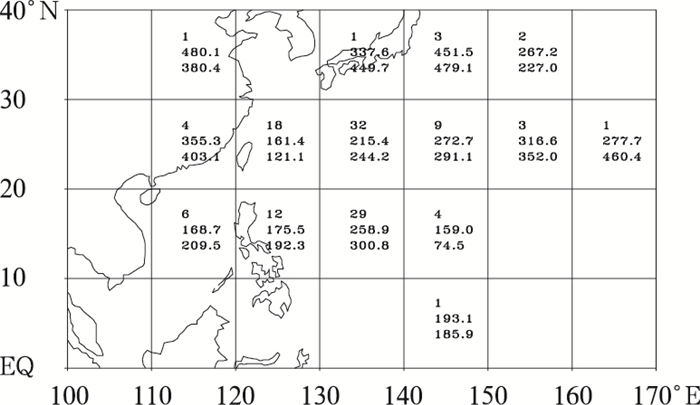
为了考察GT2.6对不同地理区域内热带气旋的预报性能,将西太平洋热带气旋发生区域(0~40°N、100~170°E)以10经/纬度为间隔划分为格点数为8×5的网格。然后按照初始涡旋的位置确定每个网格内的样本数目及相应的平均距离误差。图 5为48小时的距离误差地理分布图(24和72小时的分布情况与48小时相似,为节省篇幅未给出)。从图 5可以看出,平均距离误差的分布表现出很强的地域性,130°E以西大部分区域内的距离误差明显小于130°E以东的。特别是在靠近我国台湾省(20~30°N、120~130°E)和菲律宾以西(10~20°N、110~120°E)这两个区域内,距离误差远小于总体平均(48小时小230.7km)。在10~20°N、120~130°E内,GT2.6的预报也相当不错。而30°N以北,10~20°N、130~140°E以及20~30°N、140~170°E的距离误差显著大于总体平均。由图 1可以看出,30°N以南、130°E以西的样本多为西或西北行类样本,而30°N以北和30°N以南(特别是20°N以南)、130°E以东转向样本数明显增多。从前面分析可知,GT2.6对西或西北行样本的距离误差显著小于对转向样本的,这便在很大程度上造成了上述分布形态。而且,30°N以北的7个样本中有5个处在高纬度天气尺度系统(西风槽、高空冷涡、温带气旋、反气旋等)影响范围内(图未给出),与在中低纬相比,热带气旋与这些系统间的相互作用也更为复杂,模式对这些过程的移动特征往往难以作出准确的预报,因而会导致比较大的路径预报误差[17]。图 5还需注意的是,登陆我国海南和大陆(20~40°N、110~120°E)的5个样本平均距离误差较大,这主要是因为热带气旋登陆后,它的结构受到地形等作用,由于热带气旋登陆后强度迅速减弱,而GT2.6模式对于这些过程还不能比较好地反映出来,这也是目前热带气旋研究领域中没有解决而需要加强研究的热带气旋登陆后的路径预报问题。由以上分析可知,GT2.6对靠近我国台湾省和菲律宾的热带气旋的路径预报有较高的参考价值,但对于热带气旋进入中高纬度(30°N以北)、太平洋东部和中南部(10~20°N、130~140°E和20~30°N、140~170°E)以及登陆后(进入20~40°N、110~120°E)的预报结果在实际应用中要慎重考虑。
|
图 5 GT2.6和GT2.1 48小时距离误差地理分布 每格内数字从上到下为别表示样本数、GT2.6的距离误差和GT2.1的距离误差(单位:km) |
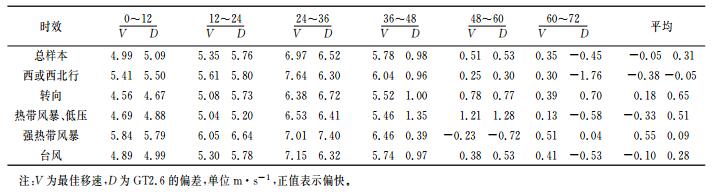
由于最佳路径的时间分辨率为6小时,本文使用6小时间隔的距离计算移速。然后将路径以12小时为间隔分段,计算各段的平均移速。总体平均、不同路径类型和不同强度的最佳路径移速及模拟移速见表 2。
|
|
表 2 GT2.6的移速偏差 |
从表 2可以看出,GT2.6的平均预报移速在48小时内都比最佳路径移速偏快,偏快程度随预报时间的增长而减小,48小时后转为偏慢。前48小时偏快的样本占总数的约55%,48小时后偏慢的样本占总数的约41%。其72小时平均移速偏快0.31m·s-1。热带气旋的移速在很大程度上取决于引导流速(通常比引导流速快约1m·s-1)[18],因此GT2.6的移速偏差主要是由其对背景环流预报不准确造成的。值得注意的是,GT2.6在初始的12小时内偏快最多(近1m·s-1),偏快样本的比例也很高(71.4%)。这意味着对大部分样本,在预报初始12小时,只移速偏差就可能产生近40km的距离误差。而初始阶段的预报移速受初始资料中的初始移速影响很大,因此很有必要在涡旋初始化过程中纠正其初始移速[10]。分类样本中,转向类和热带气旋和热带低压类的72小时内平均移速偏差较大,与它们较大的初始移速偏差对应,这也印证了初始化过程对GT2.6路径预报的重要性。
以上分析可知,GT2.6在前12小时距离误差较大,其预报技巧随预报时间的增加而显著提高,24小时后表现出良好的路径预报性能。GT2.6对西或西北行样本和登陆样本的路径有不错的预报效果,而对转向样本和强度较大样本的表现较差。向西的系统偏差使GT2.6对西或西北行样本的预报移速偏快,而对转向样本的预报则倾向于低估转向。用系统偏差订正GT2.6对转向类样本的预报路径可获得明显的改进。GT2.6的预报移速在48小时内都比最佳路径移速偏快,48小时后转为偏慢。有必要采取措施减小其显著的初始移速偏差。GT2.6在130E以西区域的误差明显小于130°E以东的,对靠近我国台湾省和菲律宾的热带气旋的路径预报有较高的参考价值,而对于在中高纬度(30°N以北)、东部和中南部太平洋(10~20°N、130~140°E和20~30°N、140~170°E)以及登陆后(进入20~40°N、110~120°E)的热带气旋的路径预报结果在应用时要慎重参考。
3 GT2.6和GT2.1路径预报性能比较为了考察GT2.6的路径预报性能相对GT2.1的差异,对GT2.1在2005年的业务路径预报也做如上分析,选用样本保持一致。由于GT2.1的业务预报时效为48小时,只比较两个版本的前48小时表现。
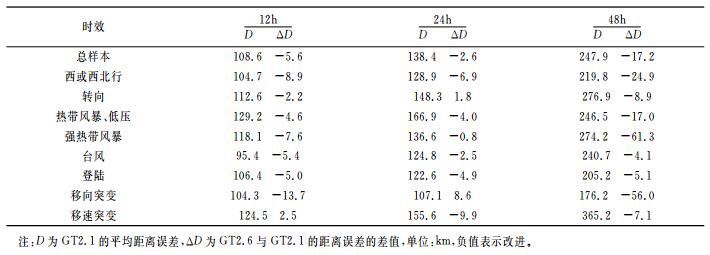
平均距离误差:表 3为两版本的平均距离误差对比。48小时内,两版本对所有样本预报误差的标准方差接近(未给出),说明两版本的预报稳定性相当[13]。前24小时,GT2.6和GT2.1误差很接近。48小时GT2.6比GT2.1改进达17km,是GT2.1距离误差的7%。
|
|
表 3 GT2.6与GT2.1的距离误差对比 |
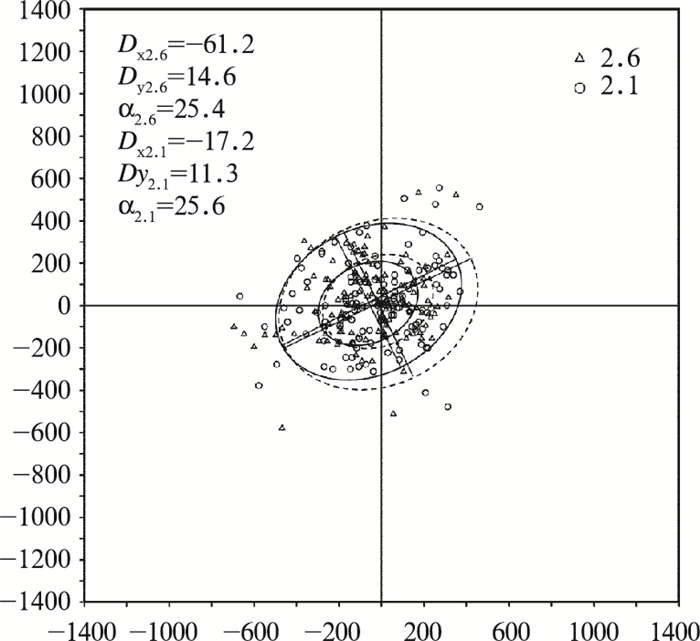
系统偏差对比:两版本在48小时内的偏差分布形态相似(只给出48小时的,图 6),且都有向西的系统偏差(图 4b)。GT2.6的系统偏差随预报时间向西增大,48小时达近65km,GT2.1则一直未超过20km。
|
图 6 GT2.6和GT2.1对所有样本的48小时偏差分布 实线椭圆和虚线椭圆分别为GT2.6和GT2.1的概率椭圆,其余说明同图 3 |
距离误差地理分布对比:GT2.6和GT2.1的距离误差地理分布形态在前24小时基本一致(图未给出)。48小时(图 5),GT2.6在大部分区域都有所改进,在样本数最集中(占总数的48.4%)的10~30°N、130~140°E内改进幅度接近30km。
移速偏差对比:两版本的移速偏差对比见表 4。在48小时内,两版本的预报移速都比最佳路径移速偏快,在预报的前12小时二者接近,12~36小时GT2.6比GT2.1偏慢,更接近于最佳路径移速,36小时后则相反。两版本的48小时内平均移速偏差接近。
|
|
表 4 GT2.6和GT2.1的移速偏差对比。 |
GT2.6改进的显著性:从以上基于2005年样本的比较结果可以看出,GT2.6对所有样本的48小时路径预报相对于GT2.1有改进。由配对t检验(信度水平设为95%)知[10],GT2.6对所有样本改进达到了显著水平。
4 结论和讨论本文使用2005年西太平洋和南海的热带气旋个例对GRAPES_.1的升级版GRAPES_TCM2.6从平均距离误差、系统偏差、距离误差的地理分布和平均移速误差等方面检验了其路径预报性能。结果表明,GT2.6在前12小时距离误差较大,其预报技巧随预报时间的增加而提高,24小时后表现出良好的路径预报性能。GT2.6对西或西北行类及登陆类样本的预报效果不错,而对转向类和强度为台风类个例的表现要比总体误差偏大。GT2.6有向西的系统性偏差,且基本上随预报时间的增长该偏差向西增大,72小时达到近90km,GT2.6对西或西北行样本的预报移速偏快,而对转向样本则倾向于低估转向。用系统偏差订正GT2.6对转向类样本的预报路径可获得明显的改进。GT2.6对130°E以西区域的样本预报表现较好,特别对靠近我国台湾省和菲律宾的热带气旋的路径预报有较高的参考价值,但对于在中高纬度(30°N以北)、东部和中南部太平洋(10~20°N、130~140°E和20~30°N、140~170°E)以及登陆后(进入20~40°N、110~120°E)的热带气旋,预报员在参考GT2.6的预报路径时需要慎重考虑。GT2.6的总体平均预报移速在48小时内都比最佳路径移速偏快,初始12小时内偏快最多(近1m·s-1),48小时后转为偏慢。GT2.6对转向类和热带风暴和热带低压类的72小时平均移速偏差较大。
比较GT2.6和GT2.1的前48小时路径预报性能发现,两版本的预报稳定性相当。前24小时两版本的距离误差接近,在48小时GT2.6对所有样本有显著改进,预报的平均距离误差减少7%。两版本具有比较相似的系统偏差特征。
由性能检验可知,GT2.6路径预报性能的主要不足有:初始(12小时)预报误差较大,对转向类样本和强度较大样本(台风类)的预报效果改进不明显。初步分析表明,GT2.6的初始移动的较大偏差,对热带气旋环流预报偏差较大,对背景环流的位置、强度预报还不够准确。因此,下一步的工作应该围绕初始场的改进,比如,在初始场中加入引导向量改进初始移动、采用GFDL的涡旋分离方案[19]、加入非对称Bogus涡旋[13-20]、适当扩大预报区域,并适当选取预报区域起始位置等均可以进一步提高GT2.6的路径预报技巧。
| [1] |
Franklin, J. L. . 2005 National Hurricane Center Forecast Verification Report[OL]. Available online at http://www.nhc.noaa.gov/verification/pdfs/Verification_2005.pdf, 2006.
|
| [2] |
李佳, 于润玲, 马雷鸣. 2005年西北太平洋热带气旋综述[J]. 大气科学研究与应用, 2006, 01(01): 1-15. |
| [3] |
许映龙, 刘震坤, 董林. 2002年西北太平洋和南海热带气旋路径主客观预报评价[J]. 气象, 2005, 31(06): 43-46. |
| [4] |
殷鹤宝.正规模初始化及其及其在东海台风模式中的实验[M].台风、暴雨业务数值预报方法和技术研究, 北京:气象出版社, 1996, 59-66.
|
| [5] |
王康玲. 南海区域台风路径数值预报业务模式研究实验[M]. 台风、暴雨业务数值预报方法和技术研究, 北京: 气象出版社, 1996.
|
| [6] |
陈德辉, 薛继善, 沈学顺, 等. 新一代数值预报系统(GRAPES)研究及其初步应用试验[C]. 数值天气预报新理论新方法及应用学术研讨会, 论文摘要汇编, 2004: 87-91.
|
| [7] |
陈建萍. 全球区域同化预报系统的使用及其数值模拟[J]. 江西气象科技, 2005, 28(2): 10-12. |
| [8] |
叶成志, 欧阳里程, 李象玉, 等. GRAPES中尺度模式对2005年长江流域重大灾害性降水天气过程预报性能的检验分析[J]. 热带气象学报, 2006, 22(04): 83-89. |
| [9] |
黄伟, 端义宏, 陈德辉, 等. 热带气旋路径数值模式(GRAPES-TCM)业务试验性能分析. 提交《气象学报》.
|
| [10] |
Mark Demaria, Miles B. Lawrence, James T. Kroll. An Error Analysis of Atlantic Tropical Cyclone Track Guidance Models[J]. Weather and Forecasting, 1990, 5: 47-61. DOI:10.1175/1520-0434(1990)005<0047:AEAOAT>2.0.CO;2 |
| [11] |
Charles S., Joseph M.Pelissier.. An Analysis of Atlantic Tropical Cyclone Forecast Errors, 1970-1979[J]. Monthly Weather Review, 1981, 109: 1248-1266. DOI:10.1175/1520-0493(1981)109<1248:AAOATC>2.0.CO;2 |
| [12] |
Neumann C. J. . An alternate to the HURRAN tropical cyclone forecast system[R]. NOAA Tech. Memo. NWS SR-62, 1972, 32 pp.
|
| [13] |
ohnny C.L.Chan, Wai-Kau Kay.. Performance of the United Kingdom Meteorolo gical Office Global Model in Predicting the Movement of Tropical Cyclones[J]. Weather and Forecasting, 1993, 8: 326-336. DOI:10.1175/1520-0434(1993)008<0326:POTUKM>2.0.CO;2 |
| [14] |
刘爱鸣. 台风移向突变诊断预报方法与1994年试用结果[M]. 台风及其灾害性天气业务预报方法的研究.北京: 气象出版社, 1996: 207-212.
|
| [15] |
夏丽花. 一种台风移速突变的诊断预报方法[M]. 台风及其灾害性天气业务预报方法的研究.北京: 气象出版社, 1996: 231-235.
|
| [16] |
Tracy J D. Accuracy Of Atlantic Tropical Cyclone Forecasts[J]. Monthly Weather Review, 1966, 94: 407-418. DOI:10.1175/1520-0493(1966)094<0407:AOATCF>2.3.CO;2 |
| [17] |
Lester E.Carr Ⅲ, Russell L.Elsberry.. Dynamical Tropical Cyclone Track Forecast Errors. Part Ⅱ: Midlatitude Circulation Influences[J]. Weather and Forecasting, 2000, 15: 662-681. DOI:10.1175/1520-0434(2000)015<0662:DTCTFE>2.0.CO;2 |
| [18] |
Johnny C.L., ChanWilliam M.Gray. Tropical Cyclone Movement and Surrounding Flow Relationships[J]. Monthly Weather Review, 1982, 110(1354): 1374. |
| [19] |
Yoshio Kurihara, Morris A. Bender, Robert E. Tuleya. Improvements in the GFDL Hurricane Prediction System[J]. Monthly Weather Review, 1995, 123(2791): 2791-2801. |
| [20] |
Melinda S.Peng, Der-Song Chen, Simon W. Chang. Improvement of Numerical Prediction of Typhoon Tracks in the Western North Pacific Basin near Taiwan[J]. Weather and Forecasting, 1995, 10: 411-424. DOI:10.1175/1520-0434(1995)010<0411:IONPOT>2.0.CO;2 |
 2007, Vol. 33
2007, Vol. 33