2. 成都信息工程学院 高原大气与环境研究中心四川省高校重点实验室;
3. 四川甘孜州气象局;
4. 新疆气象台
2. Center of Plateau Atmospheric and Environmental Research, Chengdu University of Information Technology;
3. Ganzi Meteorological Office, Sichuan Province;
4. Xinjiang Meteorological Observatory
我国地处著名的东亚季风气候区,一般每年6—7月当东亚夏季风向北推进时,我国的江淮流域常常会出现一段连阴雨天气,由于此时正值江南梅子黄熟季节,故称“梅雨”,又因这时空气湿度很大,百物极易获潮、霉烂,因而又有“霉雨”之称[1]。梅雨是我国江淮流域春末夏初过渡季节中的重要天气气候现象[2],因此,梅雨一直是吸引广大气象学者研究的重要课题,已取得不少有意义的研究成果[3-5]。占地球表面积三分之二以上的海洋不仅是驱动大气运动的能量直接供应者和调节器, 而且还是大气中水汽的主要源地,海洋的热力和动力特性又使它对大气变化具有独特的“记忆功能”和“低通滤波”作用,因此,海温异常一直被认为是引起环流和气候异常的一个重要因素,它在全球气候变化中扮演着一个非常重要的角色,越来越引起人们的高度重视。早在1950—1960年代,Namias[6]和Bjerknes[7]就提出北太平洋的海温异常对大气环流异常的维持和加强的反馈作用,并把海温异常的研究引入到热带海洋,提出热带海温与全球大气环流和气候变化的遥相关概念,逐步使热带海洋大气相互作用的研究成为近代大气科学的一个重要研究领域。此后,海气相互作用的研究取得了迅速进展,世界气候研究计划[8](WCRP)在1995年推出的气候变率及其可预测性(CLIVAR)研究计划中将海洋置于一个举足轻重的位置。影响江淮梅雨异常的因子有很多,其中海温已被认为是最重要的影响因子之一。王谦谦、钱永甫[9-10]研究指出:海温异常的区域和量值不要求很大,所引起的感热量值也不大,但却是气候异常的一种重要的触发因子。本文运用江苏省气象台给出的梅雨量资料,采用EOF[11]、合成分析、SVD[12-14]、Monte-Carlo显著性检验[15]等多种诊断分析方法,对江淮梅雨与西太平洋海温的关系进行了详细讨论,这对探寻梅雨影响因子的强信号,为江淮梅雨的预测水平提供思路和理论依据。
1 资料(1) 江苏省气象局整编的江淮流域1954—2001年共48年梅雨量资料。
(2) 美国NCEP/NCAR再分析资料中1953.01—2001.12全球逐月海温格点资料,网格距2°×2°。本文中的冬季指前1年的12月至当年的2月。
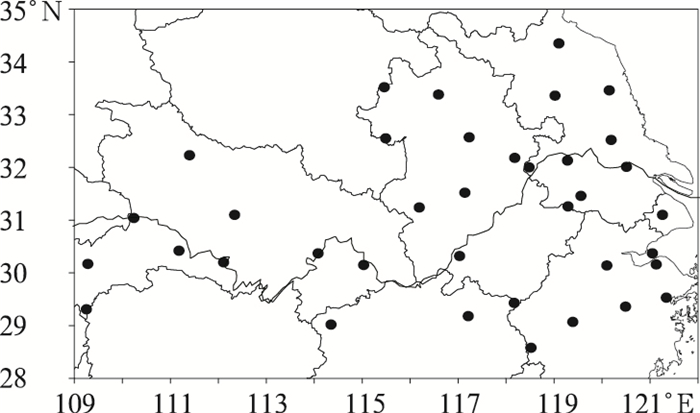
2 梅雨量变化的空间分布特征 2.1 江淮流域客观代表站的选取利用江苏省气象局整编的江淮流域梅雨量资料,在消除台站迁移、经过均一性检查和严格质量控制基础上,按照所研究区域内站点尽量多、时段尽量长的原则,选取江淮流域(28~34°N、110~123°E)范围内37个代表站,其空间分布如图 1所示。
|
图 1 江淮流域37个代表站的空间分布 |
由图可见,站点分布均匀,它包括了江淮流域五省一市的大部地区,即苏、皖、浙、鄂的大部、赣北以及上海市,它们分别是:光化、巴东、钟祥、恩施、宜昌、荆州、武汉、来凤、修水、连云港、亳县、宿县、淮安、射阳、阜阳、蚌埠、滁县、南京、镇江、东台、南通、霍山、合肥、常州、溧阳、上海、黄石、安庆、杭州、乍浦、慈溪、景德镇、黄山、金华、嵊州、鄞县、衢州。
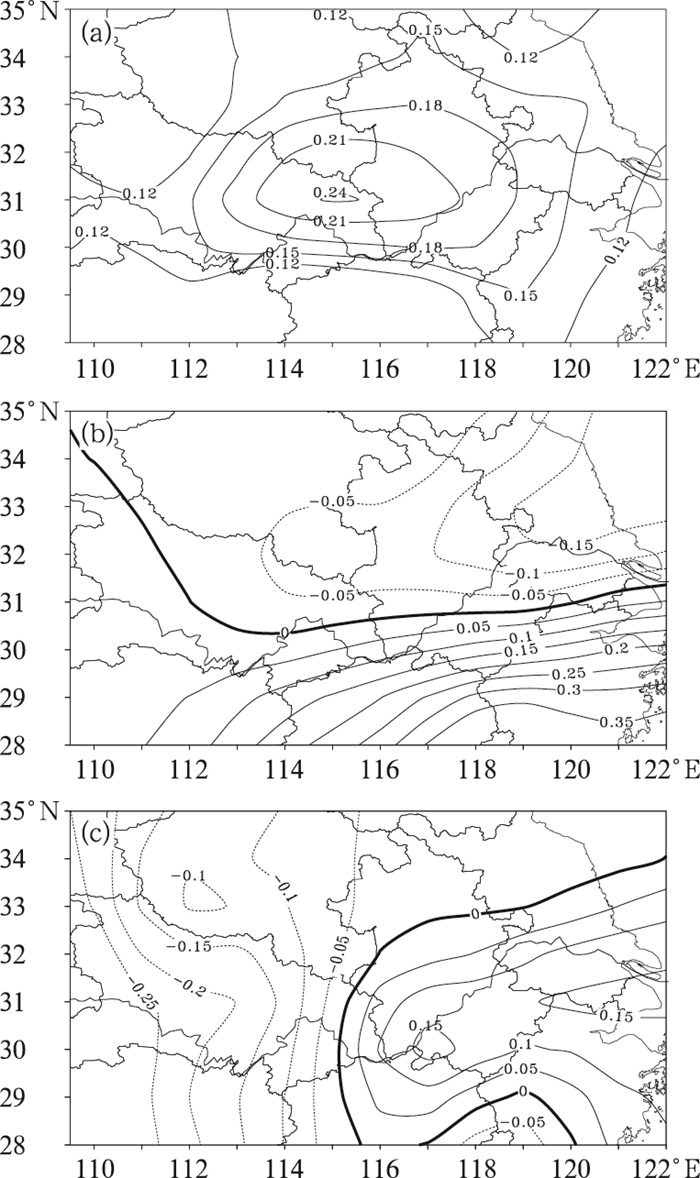
2.2 梅雨量的空间分布对江淮流域37站1954—2001年共48年梅雨量距平进行EOF分析,得到方差贡献率较大的前3个模态的空间分布(图 2),它反映出江淮梅雨量的几种主要的大范围空间分布型,其累积方差贡献率为73.4%,利用North等[16]的经验方法对其取样误差进行评估,EOF结果特征值收敛很快,表明满足能量按自由度均分,稳定可分,因此具有实际的物理意义。第1模态(图 2a)占总方差的56.3%,表明梅雨量的空间分布型为全区一致,其振幅高值中心位于江淮流域中部淮河流域以南和长江流域以北的皖南和鄂北地区,是江淮梅雨量最主要的空间分布型式。第2模态(图 2b)占总方差的11.5%,表明江淮梅雨量大致以31°N为界呈南多(少)北少(多)的反位相变化,反映了江淮梅雨量南、北部之间的空间局地差异。第3模态(图 2c)占总方差的5.7%,表明江淮梅雨量大致以115°E为界呈东多(少)西少(多)的反位相变化,反映了江淮流域梅雨量东、西部之间的空间局地差异。以上分析表明,采用一级近似将江淮流域梅雨量作为一个整体来分析是合理的。
|
图 2 梅雨量EOF分解前3个模态的空间分布 a.第1模态; b.第2模态; c.第3模态 |
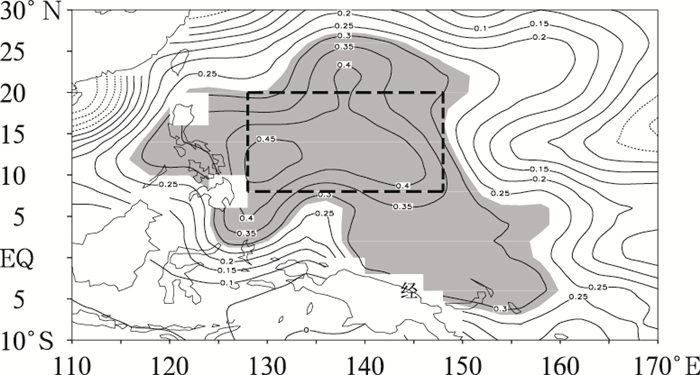
为寻找江淮梅雨与全球海温的显著相关海区和关键时段,首先将江淮梅雨量做区域平均为一个点,然后用1954—2001年共48年梅雨量与全球1953—2001年共49年超前1年至当年共24个月海温逐月滑动求相关,可以得到24张逐月相关图(图略),经过对比分析,综合考虑到相关系数的大小、相关的稳定性、持续时间及可预报性等因素,可以得到与梅雨量相关显著的全球海域(图 3),由图 3可知:显著相关海域位于菲律宾群岛以东的西太平洋暖池区,相关系数达0.35以上,通过α=0.05显著性检验,而梅雨量与全球其它海域相关不够稳定、持续时间短,相关系数小。因此,将影响江淮梅雨的海温关键区初选为西太平洋暖池区(8~20°N、126~146°E), 显著相关时段为前1年的12月至当年的2月(以下简称冬季)。
|
图 3 梅雨量与西太平洋暖池冬季海温标准化距平(SSTA)的相关分布 阴影区通过α=0.05显著性检验, 方框区为显著关键区 |
为寻找冬季西太平洋海温空间型态,对西太平洋1954—2001年冬季区域平均标准化距平(SSTA)进行EOF分解,得到方差贡献率较大的前2个特征向量,其累积方差贡献率为46.85%,并根据North等[16]提出的经验方法对其取样误差进行评估,结果表明满足能量按自由度均分,具有实际的物理意义。图 4给出EOF分解的前2个模态的空间分布。
|
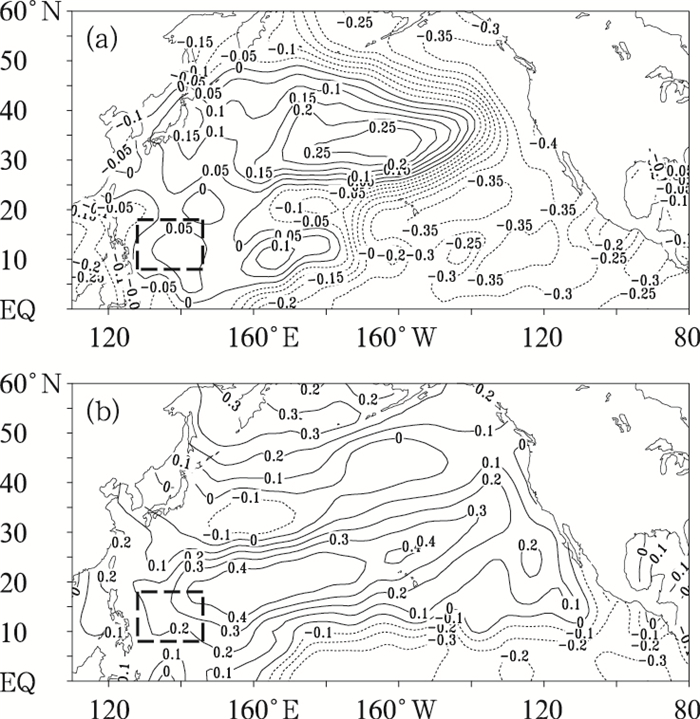
图 4 西太平洋冬季海温标准化距平(SS-TA)EOF分解前2个模态空间分布 a.第1模态; b.第2模态 |
由图 4可知:第1模态(图 4a)占总方差的22.96%,反映的主要是冬季西太平洋海温的ENSO模态,代表了冬季西太平洋海温的主要分布型,具体表现为西太平洋暖池区和中高纬度的北太平洋海温距平与赤道中东太平洋、白令海至阿拉斯加湾冷流区的反位相变化,且高振幅区位于夏威夷群岛檀香山以北的北太平洋海域。第2模态(图 4b)占总方差的11.96%,反映的主要是冬季西太平洋海温的异常模态,代表了西太平洋暖池、北太平洋中高纬度与低纬度赤道中东太平洋海温的局地差异。
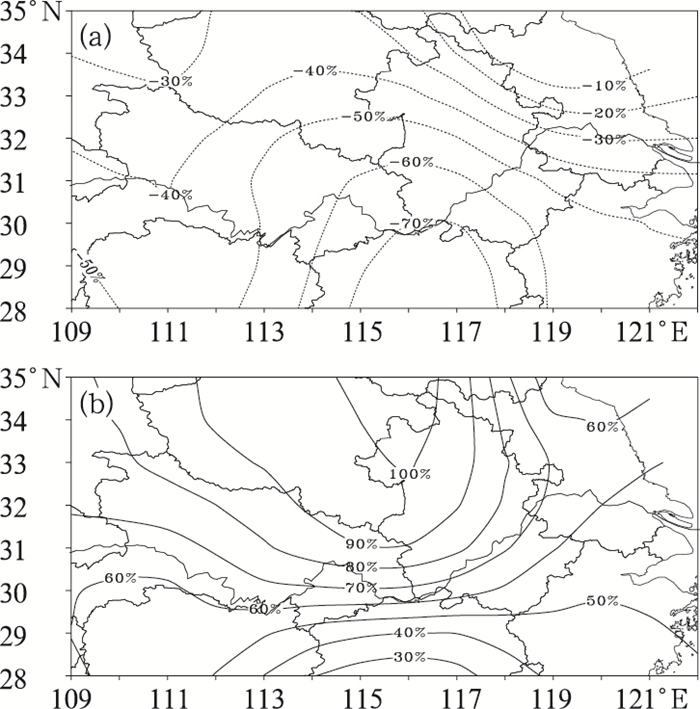
3.3 西太平洋暖池海温异常梅雨量合成分析由1954—2001年近48年西太平洋暖池冬季区域平均海温标准化距平SSTA的年际变化曲线(图略),以海温标准化距平大于1.0倍标准差为暖水年,小于-1.0倍标准差为冷水年的标准,选出西太平洋暖池区海温冷水年5年(分别是1958年、1959年、1965年、1972年和1976年),暖水年6年(分别是1954年、1988年、1991年、1996年、1998年和2001年)。图 5给出西太平洋暖池冬季海温异常偏冷(暖)当年梅雨量距平百分率合成分布。
|
图 5 西太平洋暖池冬季海温偏冷(a)、偏暖(b)年当年梅雨量距平百分率合成 |
由图可见:西太平洋暖池冬季海温异常偏冷,当年江淮梅雨量距平百分率空间分布为全区一致为负,距平百分率介于-10%~-70%之间,其中江淮南部地区距平百分率偏少大于江淮北部地区,梅雨量距平百分率最小值区主要位于皖南和赣北地区,梅雨量距平百分率减少40%~60%以上。西太平洋暖池冬季海温异常偏暖则相反,整个江淮流域梅雨量距平百分率全区一致为正,距平百分率介于30%~100%之间,江淮北部地区梅雨量距平百分率大于江淮南部地区,其中长江以北地区梅雨量距平百分率大于60%,最大值中心位于苏北、皖北及鄂北地区。从以上分析可见:当西太平洋暖池冬季海温异常偏冷时,当年江淮流域梅雨量较常年偏少1~7成,江淮北部地区偏少比江淮南部地区偏少更甚。当西太平洋暖池冬季海温异常偏暖时,当年江淮流域梅雨量较常年偏多3成至1倍,其中江淮北部地区梅雨量偏多大于江淮南部地区。
3.4 西太平洋暖池海温与梅雨量的SVD分解上文的合成分析结果是否具有统计意义,下面分别对1954—2001年共48年西太平洋暖池冬季海温SSTA与梅雨量标准化距平进行SVD分解,以揭示其与梅雨量的关系,同时对上文合成分析的结果进行显著性检验。分别以西太平洋暖池1954—2001年共48年冬季SSTA为左场,以当年48年江淮梅雨量标准化距平为右场,进行SVD分解。表 1给出SVD分解结果前3个模态数据信息。
|
|
表 1 梅雨量与西太平流暖池海温SVD分解前3个模态数据信息 |
由表 1可以看出,第1模态解释协方差平方和百分率为96.31%,第1模态展开系数之间的相关系数为0.49,通过0.05显著性检验,第1模态解释左场的方差百分比最大,为72.62%, 第1模态解释右场的方差百分比最大,为49.57%,因此第1模态能够反映出江淮梅雨量与西太平洋暖池冬季海温之间相关关系的主要特征,由于同类相关图与异类相关图相似,故下面主要分析SVD分解第1模态的异性相关系数分布。
由SVD分解第1模态异性相关系数分布(图 6)可知:冬季西太平洋暖池SSTA异性相关系数为负,通过0.05显著性检验,其异性相关系数绝对值最大值中心达0.4以上。梅雨量异性相关系数除江西北部外,江淮大部地区异性相关系数都为负值且通过0.05显著性检验,其最大负值区位于长江以北的江淮北部地区,相关系数绝对值达0.7以上。从相应的时间系数分布也可以看出,两者的时间变化趋势也基本一致,呈同位相变化,模态相关为0.41,通过0.05显著检验,并且1954—2001年48年来江淮梅雨量丰、枯梅年在图中均有较为清晰的反映,强度也拟合得较好。从以上分析可见:西太平洋暖池冬季海温与梅雨量存在显著正相关关系,当西太平洋暖池冬季海温异常偏暖时,除江西北部外,当年江淮大部地区梅雨量异常偏多,反之亦然。这与前面西太平洋暖池海温异常偏冷、偏暖年当年江淮梅雨量合成分析的结果完全一致,进一步说明合成分析的结果是有统计意义的。

|
图 6 西太平洋暖池冬季SSTA与梅雨量SVD分解第1模态的异性相关系数及相应的时间系数 a.西太平洋暖池; b.梅雨量; c.时间系数;阴影区通过0.05的Monte-Carlo显著性检验 |
(1) 点相关分析表明与梅雨量存在显著相关的全球海域关键区位于菲律宾群岛以东的西太平洋暖池区(8~20°N、126~146°E),关键影响时段为前1年的12月至当年的2月,相关系数通过0.05的Monte-Carlo显著性检验。
(2) 合成分析表明西太平洋暖池冬季海温异常偏暖(冷),当年梅雨量异常偏多(少)。
(3) SVD分析结果表明:西太平洋暖池冬季海温与梅雨量存在显著正相关关系,西太平洋暖池冬季海温异常偏暖,当年梅雨量异常偏多,反之亦然,SVD分解结果与合成分析的结果完全一致。
| [1] |
朱乾根, 林锦瑞, 寿绍文, 等. 天气学原理和方法[M]. 北京: 气象出版社, 2000: 350.
|
| [2] |
周曾奎. 江淮梅雨[M]. 北京: 气象出版社, 1996: 3.
|
| [3] |
林春育. 关于梅雨讨论中的几个问题[J]. 气象, 1981, 7(7): 12-14. DOI:10.7519/j.issn.1000-0526.1981.07.004 |
| [4] |
姚学祥, 王秀文, 李月安. 非典型梅雨与典型梅雨对比分析[J]. 气象, 2004, 30(11): 38-42. |
| [5] |
毛文书, 王谦谦, 葛旭明, 等. 近116年江淮梅雨异常及其环流特征分析[J]. 气象, 2006, 32(6): 84-90. |
| [6] |
Namias J. Large-scale air-sea interaction over the North pacific from summer (1962) through the subsequent winter[J]. J. Geophysical Research, 1963, 68(22): 6171-6186. DOI:10.1029/JZ068i022p06171 |
| [7] |
Bjerknes J.A. Possible response of the atmospheric Hadley circulation to equatorial anomalies of ocean temperature[J]. Tellus, 1996, 18(4): 820-829. |
| [8] |
World Climate Research Program. A study of climate variability and predictability[R]. WCRP-CLIVAR WMO/TD, 1995: 690.
|
| [9] |
王谦谦, 钱永甫. 1991年太平洋海温异常对降水影响的数值试验[J]. 南京气象学院学报, 1995, 18: 200-205. |
| [10] |
王谦谦, 钱永甫. 1991年夏季江淮洪涝成因的数值试验—西太平洋海温异常的影响[J]. 气象学报, 1995, 53(6): 595-603. |
| [11] |
黄嘉佑. 我国夏季气温、降水量场的时空分析特征[J]. 大气科学, 1991, 15(3): 124-132. |
| [12] |
Wallace J.M., Smith C, Bretherton C.S. Singular value decomposition of winter time sea surface temperature and 500hPa height anomalies[J]. J.Climate, 1992, 5(6): 561-576. DOI:10.1175/1520-0442(1992)005<0561:SVDOWS>2.0.CO;2 |
| [13] |
Bretherton C.S, Smith C, Wallace J.M. An inter-comparison of methods for finding coupled patterns in climate data[J]. J.Climate, 1992, 5(6): 541-560. DOI:10.1175/1520-0442(1992)005<0541:AIOMFF>2.0.CO;2 |
| [14] |
丁裕国, 江志红. SVD方法在气象场诊断分析中的普适性[J]. 气象学报, 1996, 54(3): 365-375. DOI:10.11676/qxxb1996.037 |
| [15] |
施能, 魏凤英, 封国林, 等. 气象场相关分析及合成分析中蒙特卡洛检验方法及应用[J]. 南京气象学院学报, 1997, 20(3): 355-358. |
| [16] |
North G R, Bell T L, Cahalan R F. Sampling errors in the estimation of the empirical orthogonal functions[J]. Mon.Wea.Rev, 1982, 110(7): 699-706. DOI:10.1175/1520-0493(1982)110<0699:SEITEO>2.0.CO;2 |
 2007, Vol. 33
2007, Vol. 33 