2. 中国气象局大气探测重点开放实验室;
3. 澳大利亚联邦科工组织水资源研究所;
4. 中国科学院水土保持与生态环境研究中心
2. CMA Key Laboratory of Atmospheric Sounding-KLAS;
3. CSIRO Land and Water, Canberra Australia;
4. Institute of Soil and Water Conservation, Chinese Academy of Science and Ministry of Water Resource
气候数据作为环境因子是气象、农业、林业、水利、生态环境建设等研究领域的基础,气候表面、特别是栅格形式的表面,如面降水量、气温趋势面等,是多种地学模型和气候学模型的主要参数。准确的气候信息空间分布理论上可由高密度站网采集,但气象测站空间分布不均(以县站为采集点),密度不足(最少几十公里),因此,站点外区域气象数据通常由邻近测站的观测值以一定的数学方法估算,即气象要素空间插值。近年来,气象要素插值已被作为专门的议程进行探讨和研究,主要集中于插值算法理论[1-4]、各种方法应用与结果比较[5-9]以及引入胁迫因子增加插值精度的探讨[10-14]等几个方面。在所有方法中,基于地统计插值技术的Kriging法和薄盘样条法TPS(Thin Plate Spline)最为适用,这些技术建模只将空间分布作为观测数据的函数而不需要其先验知识和物理过程,有效提高了插值的准确度[5]。Hutchinson等从理论上分析了样条法和Kriging法的不同[4],Hartkamp[2]对比了两种方法, 认为二者都容易扩展到多维空间,当半变异函数有好的选择效果或样条粗糙度稳定时,两种方法都能获得准确的插值效果,但考虑到误差估计、数据结构和计算的简便,建议在气候数据插值中使用样条法。
空间插值在一般的地理信息系统软件中都能实现,如在ARCGIS中可以实现多种方法的空间插值,但专门针对气候数据、兼顾准确性、方便性与时间序列性的系统并不多。澳大利亚科学家Hutchinson基于薄盘样条理论编写了针对气候数据曲面拟合的专用软件ANUSPLIN[15],可以说是一个代表。ANUSPLIN允许引进多元协变量线性子模型,模型系数可根据数据自动确定,因此可以平稳地处理二维以上的样条, 这就为引入多个影响因子作为协变量,进行气象要素空间插值提供了可能。更为重要的是它能同时进行多个表面的空间插值,对于时间序列的气象数据尤其适合。ANUSPLIN已在国际上得到广泛应用[16-18],但在中国的使用仅限于与澳大利亚有合作的科研人员[12, 19-21]。该软件英文说明书专业术语生涩,对初学者有一定难度。因此很有必要对其进行全面介绍,使相关人员能快速掌握并使用。
1 ANUSPLIN介绍 1.1 模型算法局部薄盘光滑样条(Partial thin plate smoothing splines)是对薄盘光滑样条原型的扩展[22],它除普通的样条自变量外允许引入线性协变量子模型,如温度和海拔之间、降水和海岸线的关系等。
局部薄盘光滑样条的理论统计模型表述如下:
| $ {z_i} = f\left( {{x_i}} \right) + {b^T}{y_i} + {e_i}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {i = 1, \cdot \cdot \cdot , N} \right) $ | (1) |
zi是位于空间i点的因变量;xi为d维样条独立变量,f是要估算的关于xi的未知光滑函数;yi为p维独立协变量;b为yi的p维系数;ei为具有期望值为0且方差为wiσ2的自变量随机误差;wi是作为权重的已知局部相对变异系数,σ2为误差方差,在所有数据点上为常数,但通常未知[16]。
由式(1)可见,当式中缺少第二项,即协变量(p=0)时,模型简化为薄盘光滑样条原型;当缺少第一项独立自变量时,模型变为多元线性回归(ANUSPLIN中不允许这种情况出现)。事实上薄盘样条函数可以理解为广义的标准多变量线性回归模型,只不过其参数是用一个合适的非参数化光滑函数代替[15]。
函数f和系数b通过最小二乘估计来确定:
| $ {\sum\limits_{i = 1}^N {\left( {\frac{{{z_i} - f\left( {{x_i}} \right) - {b^T}{y_i}}}{{{w_i}}}} \right)} ^2} + \rho {J_m}\left( f \right) $ | (2) |
其中Jm(f)是函数f(xi)的粗糙度测度函数,定义为函数f的m阶偏导(在ANUSPLIN中称为样条次数,也叫糙度次数),ρ是正的光滑参数, 在数据保真度与曲面的粗糙度之间起平衡作用,通常由广义交叉验证GCV(generalized cross validation)的最小化来确定,也可以用最大似然法GML(Generalised max likelood)或期望真实平方误差MSE(expected true square error)最小化确定[15]。Wahba[1]综合论述了选择合适平滑参数的重要性。GCV计算可采用“one point move”方法,依次移去一个样点,用剩余样点在一定的光滑参数下进行曲面拟合得到该点的估测值,再计算观测值与估测值的方差。ANUSPLIN中同时提供了GCV和GML两种选择平滑参数的判断方法。
1.2 ANUSPLIN流程ANUSPLIN系统由FORTRAN语言编写,包括8个程序模块(图 1),每个程序的含义如表 1。其执行过程为:

|
图 1 ANUSPLIN数据处理流程图 |
|
|
表 1 ANUSPLINA程序模块意义 |
(1) 若输入数据站点少于2000时,执行SPLINA命令,生成日志与列表(Log file and List file)、误差协方差(Error covariance file)、表面系数(Surface coefficient file)、优化参数(Optimisation parameters file)和残差(Large residual file)等5个文件。
(2) 执行LAPGID(或LAPPNT)命令, 由误差协方差、表面系数文件得到预测表面和标准误差表面(或者预测表面和标准误差点文件)。
(3) 执行GCVGML命令,由光滑参数文件得到GCV或GML点文件。
而对大于2000个站点的情况,可用SELNOT命令将数据分成若干个节点,再执行SPLINB命令,后续过程与小于2000个站点的情况一致。命令执行可以在DOS下按提示一步步进行,也可以生成批处理文件*.cmd文件(如表 3、表 4)一次执行。
1.3 ANUSPLIN输入、输出格式输入文件:包含了经度、纬度、高程及其它影响因子的ASCII文件,为方便起见,最好定义一定的排列序列(如表 2)。另外还有协变量文件,如ASCII格式的DEM。
|
|
表 2 1995年月最高温度数据格式(1995_Tmax_v1_SPLINA.dat) |
输出文件:光滑参数RHO,拟合数据误差列表文件(贝叶斯标准误差、模型误差和置信区间),拟合表面系数的协方差矩阵,拟合表面和误差表面等,可在执行过程中按需要设定输出内容和格式,以在ARCGIS等系统中显示。
1.4 ANUSPLIN的模型选择ANUSPLIN在日志文件(Log file and List file)中提供了一系列用于判别误差来源和插值质量的统计参数,有:观测数据统计(均值、方差、标准差等)、拟合曲面参数的有效数量估计Signal(信号自由度)、剩余自由度Error、光滑参数RHO、GCV、期望真实均方误差MSE、最大似然法误差GML、均方残差MSR、方差估计VAR及其平方根,这些可用来选择最佳模型;统计结果还给出了具有最大均方根残差(Root mean square residual)的数据点序列, 可用来进行数据质量控制,以检验并消除原始数据在位置和数值上的错误。Log文件还可记录程序的执行过程,以便发现程序执行中的问题。
Signal指示了拟合曲面的复杂程度,RHO平衡了拟合曲面的精确度与平滑度,RHO过小和Signal大于观测站点的一半或者RHO过大都预示着拟合过程找不到最优光滑参数, 说明数据点可能过于稀疏、数据存在短相关或拟合函数太过复杂,因此所选模型不适合用于插值,这些情况在ANUSPLIN中以*符号标出。在按月进行曲面拟合时,Signal的值应有平稳的月际间过渡,明显地背离过渡趋势意味着该月插值曲面可能存在系统误差,可用它进行数据初步检验, 通常表示数据中含有缺失数据[20]。
最佳模型判断标准:GCV或GML最小,模型残差比MRR或信噪比SNR(信号自由度与剩余自由度之比)最小,信号自由度小于站点的一半,模型成功率判断中无*号指示。
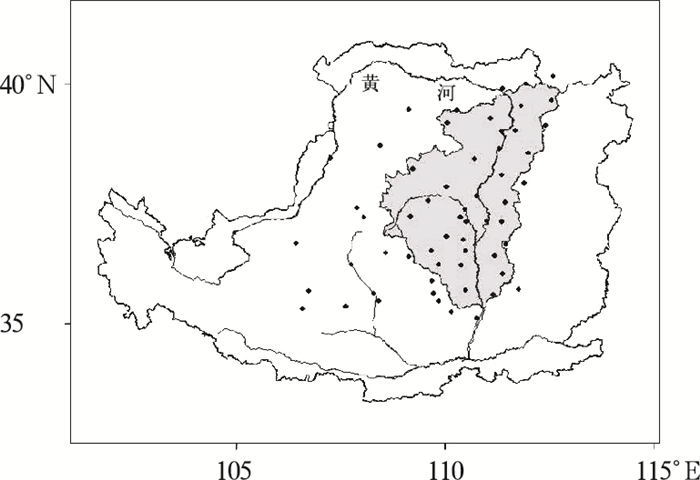
2 ANUSPLIN使用 2.1 数据准备以黄土高原多沙粗沙区温度表面插值为例。数据为黄土高原多沙粗沙区内及外围共52个气象站(见图 2)21年(1980—2000年)月最高温度,以年为单位建立21个数据文件,格式如表 2。DEM由1:25万数字地形图生成,分辨率为100米,ASCII格式。生成软件为ANUDEM[23],用它建立的“水文地貌关系修正的DEM(hydrologically correct DEMs)”与多要素TIN方法建立的DEM相比反映地表形态更为真实准确[24]。
|
图 2 研究区及站点示意图 (阴影为研究区,点为气象站) |
(1) 安装ANUSPLIN,再将C:\anusplin4.3下的SPLINA.EXE和LAPGRD.EXE文件(常用的两个命令)拷入自己的数据库目录,或把数据库文件拷入SPLINA和LAPGRD.EXE文件目录下。
(2) 根据要求写批处理命令文件splina.cmd和lapgrd.cmd,表 3、表 4是以生成1995年7月Tmax表面为例所写,可在文本下编辑。
|
|
表 3 1995_07_Tmax_v5_SPLINA.cmd文件及说明 |
|
|
表 4 LAPGRD.cmd文件(1995_07_Tmax_v5_LAPGRD.cmd)及说明 |
(3)执行命令
C:\anuspln43\splina<1995_07_Tmax_v5_SPLINA.cmd>1995_07_Tmax_v5_SPLINA.cmd.log
C:\anusplin43\lapgrd <1995_07_Tmax_v5_LAPGRD.cmd>1995_07_Tmax_v5_LAPGRD.log
根据.log文件查找出错原因,同时splina.log文件中还给出统计结果,可进行分析。
(4) 在ARCGIS中将输出表面ASCII文件转换成grid图像格式文件,进行显示操作。
以上是单月数据插值,也可以同时进行多个月份或多年的数据插值,只需对数据格式、输出表面个数和输出文件名进行定义即可。
2.3 插值模型选择时间序列气象要素空间插值要求既要保证每个表面的插值精度,又要保证插值模型的相对稳定性,使其在时间连续性上具有可比性。在对多个气象要素连续21年月值进行曲面插值过程中,首先选取1995年12个月进行实验(1995年为平水年,年降雨量接近历年平均)。实验模型为薄盘样条和局部薄盘样条函数的18个Spline模型(独立变量、协变量和样条次数多种组合)(表 5),x、y采用ALBERS投影,避免数据在位置上出现互相关,高程选用不同的单位,试图与x、y保持相近数量级。依据最佳模型判断标准,初步选出每个气象要素的最优待用模型,再用这些待用模型进行21年252个月插值,对个别模型通不过的月份,分析模型失败原因,利用残差分析,剔除个别残差较大的站点以使模型能够使用。
|
|
表 5 18个样薄盘光滑样条函数模型详细列表 |
对于Tmax,用初定的18个模型对1995年12个月的数据进行实验显示:不管是用GCV还是GML校验方法,用高程作为协变量的TVPTPS模型都是最佳模型。在12个月中,以GCV为校验方法产生最小残差比MRR的月份有9个,对应的局部样条函数的样条次数m=3,另外两个月份的样条次数为分别为m=2和m=1。以GML为校验方法产生最小残差比MRR的月份有7个,对应局部样条函数的样条次数m=3,剩余5个月份的样条次数分别为2和4。由此可见,选择以高程作为协变量的三变量局部薄盘光滑样条函数、样条次数为3的TVPTPS3模型能保证大部分月份插值结果最为精确。
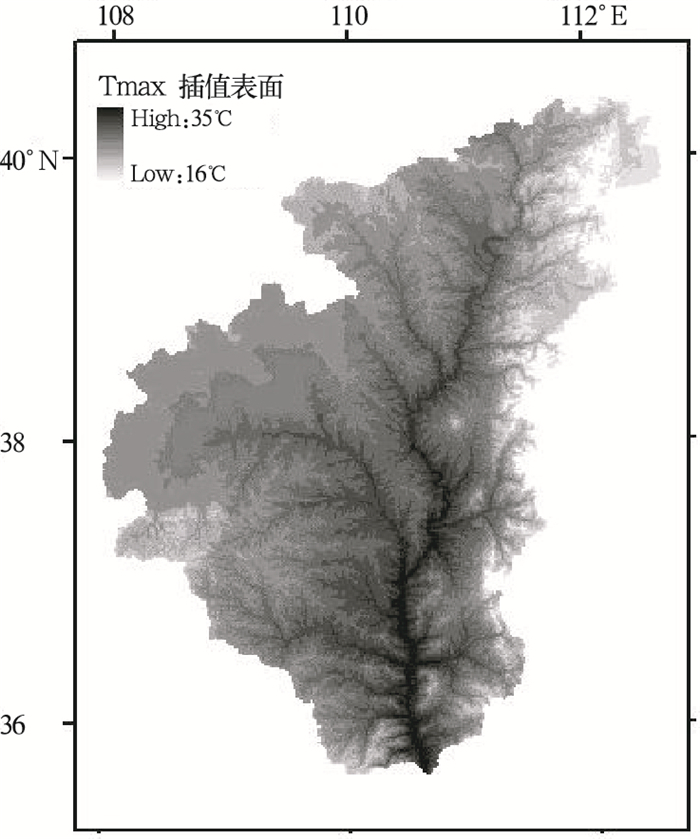
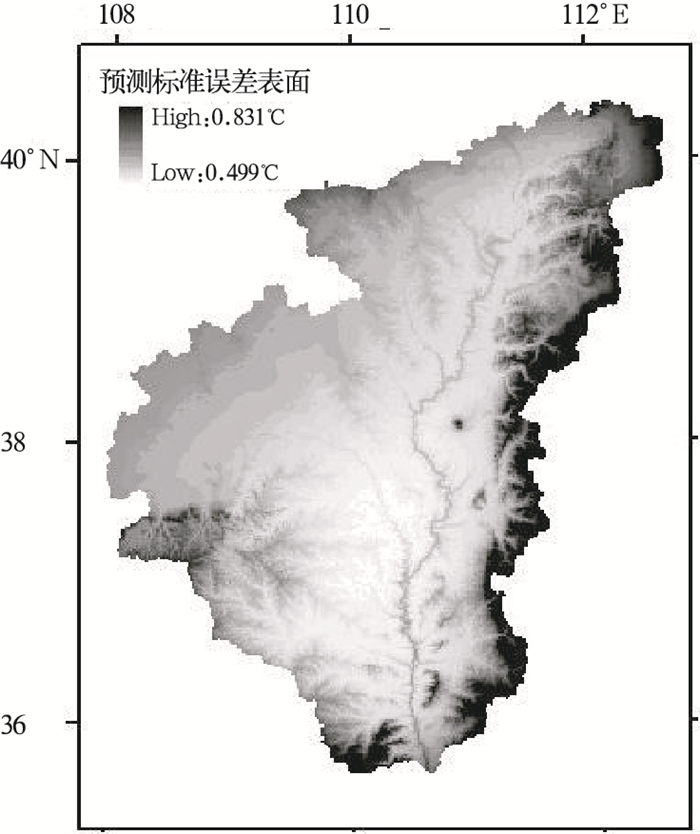
3 分析与讨论 3.1 温度表面图 3为1995年7月ANUSPLIN输出表面,图 4为预测误差表面,栅格大小为100米。从图 3可以看出,1995年7月黄土高原多沙粗沙区月平均最高温度呈现明显的地带性差异,南部高于北部,黄河沟谷地区高于其它地区,整个地区的变化范围在16~35℃之间。插值表面带有明显的DEM特征,这与常见的温度趋势面不太一样,反映温度随高程的梯度变化更为直观。图中部黄河右边的白点是一座海拔1800米左右的孤山——紫金山,插值中没有山上的气象数据,而利用高程作为协变量的插值方法可以预测其温度,这在常规方法(不考虑高程)是反映不出来的。从图 4可以看出,预测标准误差变化范围在0.499~0.831℃之间,没有地带性差异,地区边缘误差较高,其原因是边缘区域参与插值的站点较少(图 2),紫金山的误差较大是因为无山上气象数据。观测值与预测值的平均绝对误差为0.33℃,平均相对误差为1%,由此可以证明:用引入高程线性子模型的局部薄盘光滑样条函数进行温度空间插值具有很高的插值精度。
|
图 3 1995年7月最高温度插值表面 |
|
图 4 1995年7月最高温度预测标准误差表面 |
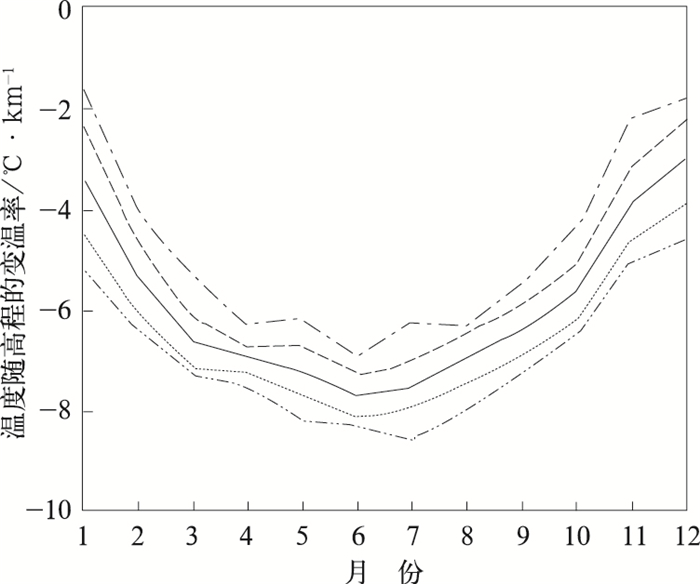
使用TVPTPS3模型进行温度插值实际上引入了高程线性子模型,也就意味着存在一个依赖于第三变量(高程)变化的线性常数,这里可理解为温度随高程的变率(Lapse rate),即高程每升高一定值,温度会随之变化多少。对252个月的lapse rate进行统计,得出温度随高程变率的季节平均值(图 5)。从图 5中可以看出,在黄土高原多沙粗沙区,月平均最高温度随高程的变化呈现很强的季节性,夏季最高,高程每升高1000m,月平均最高温度可下降近8℃,春秋季下降5℃左右,而冬季则下降3℃左右。用同样的方法进行252个月月平均最低温度Tmin空间插值,得到Tmin随高程的变化规律与Tmax基本一样,但变化范围稍小一些,在3~6.5℃之间,这与有些学者在其它地方得出的结论是一致的[10, 13, 25]。
|
图 5 Tmax(a)随高程的变率 (a)随高程的变率(实线为平均值,虚线为均值±1个标准差,点划线为月最大、最小值) |
本文简单阐述了专用气象要素空间插值软件ANUSPLN的理论基础,通过实例介绍了软件特点、系统流程和使用方法,对于从事气候、环境与GIS研究的人员了解、使用ANUSPLIN软件起到一定的指导作用,得到如下初步结论:
(1) 薄板光滑样条函数方法是目前较好的一种曲面插值方法,兼顾了插值曲面的平滑度与精确度。具有较强综合能力的空间插值软件ANUSPLIN可以兼顾不同格式的输入数据、任意调整数据的变化参数,并提供多种格式的栅格输出表面及误差表面。另外丰富的统计参数及模型诊断参数可以用来判断站点充分与否,帮助用户轻松选择最优模型。
(2) ANUSPLIN软件允许引入线性子模型作为协变量模型,这为综合考虑多个影响因素进行气象要素空间插值提供了实现工具。另外,线性子模型的线性常数反映了变量随协变量的变化情况,如在本研究中月最高温度随高程每增加1000m,夏季下降8℃,而冬季下降3℃,这使人们能更加清楚地理解各因子的关系。
(3) ANUSPLIN能同时进行多个表面插值,这为长时间序列气象要素的时空变化分析和连续动态图形显示提供了方便,能更为直观地反映气候环境的变化趋势。
| [1] |
Wahba G. Spline models for observational data[A]. Regional Conference Series in Mathematics 59, SIAM, Philadelpha. 1990.
|
| [2] |
Hartkamp A D, Kirsten D B, Stein A. Interpolation Techniques for Cliamate Variables, Geographic Information Systems series 99-01. Mexico DF: International Maize and Wheat Improvement Center (CIMMYT), 1999: 1-26.
|
| [3] |
Wackernagel H. Multivariate Geostatistics An Introduction with Applications[M]. Berlin: Springer Verlag, 1995: 377-403.
|
| [4] |
Hutchinson M F, Gessler P E. Splines -More Than Just a Smooth Interpolator[J]. Geoderma., 1994, 62: 45-67. DOI:10.1016/0016-7061(94)90027-2 |
| [5] |
Peter M, Chris D. Mapping Precipitation in Switzerland with ordinary and indicator Kriging[J]. Journal of Geographic Information and Decision Analysis, 1998, 2(2): 65-76. |
| [6] |
Fred C. Collins, Paul V. Bolstad. A Comparison of Spatial Interpolation Techniques in Temperature Estimation[A]. Proceedings of the Third International Conference/Workshop on Integrating GIS and Environmental Modeling, Santa Barbara, California. 1996.
|
| [7] |
Price D T, McKenney D W, Nalder I A, et al. A comparison of two statistical methods for spatial interpolation of Canadian monthly mean climate data[J]. Agricultural and Forest Meteorology, 2000, 101: 81-94. DOI:10.1016/S0168-1923(99)00169-0 |
| [8] |
庄立伟, 王石立. 东北地区逐日气象要素的空间插值方法应用研究[J]. 应用气象学报, 2003, 14(5): 605-615. |
| [9] |
余吉仁, 靳立亚, 彭友兵, 等. 一种求解区域平均值的权重面积设计及其应用[J]. 气象, 2006, 32(4): 52-55. DOI:10.7519/j.issn.1000-0526.2006.04.009 |
| [10] |
Lookingbill T R, Urban D L. Spatial estimation of air temperature differences for landscape-scale studies in montane environments[J]. Agricultural and Forest Meteorology., 2003, 114: 141-151. DOI:10.1016/S0168-1923(02)00196-X |
| [11] |
潘耀忠, 龚道溢, 邓磊, 等. 基于DEM的中国陆地多年平均温度插值方法[J]. 地理学报, 2004, 59(3): 366-374. DOI:10.11821/xb200403006 |
| [12] |
刘志红, TimR. McVicar, LingTaoLi, 等. 基于5变量局部薄盘光滑样条函数的蒸发空间插值[J]. 中国水土保持科学, 2006, 4(6): 23-30. |
| [13] |
Thornton P E, Running S W, White M A. Generating surfaces of daily meteorological variables over large regions of complex terrain[J]. Journal of Hydrology., 1997, 190: 214-251. DOI:10.1016/S0022-1694(96)03128-9 |
| [14] |
McVicar T R, Van Niel T G, Li L T, et al. Spatially Distributing Monthly Reference Evapotranspiration and Pan Evaporation Considering Topographic Influences[J]. Journal of Hydrology, 2007, 338: 196-220. DOI:10.1016/j.jhydrol.2007.02.018 |
| [15] |
Hutchinson M F. ANUSPLIN Version 4. 3 User Guide[M]. Canberra: The Australia National University, Center for Resource and Environment Studies 2004. http://cres.anu.edu.au/outputs/anusplin.php
|
| [16] |
Hutchinson M F. The application of thin plate splines to continent-wide data assimilation, Data Assimilation Systems, BMRC Research Report NO.27[M]. Melbourne: Bureau of Meteorology, 1991: 104-113.
|
| [17] |
Price D T, McKenney D W, Papadopol P, et al. High resolution future scenario climate data for North America[A]. American Meteorological Society Annual Meetings, Vancouver. 2004.
|
| [18] |
Hijmans R J, Cameron S E, Parra J L, et al. Very high resolution interpolated climate surfaces for global land areas[J]. International Journal of Climatology, 2005, 2: 1965-1978. |
| [19] |
McVicar T R, Li L T, Van Niel T G, et al. Spatial Interpolation of Time Series Point Hydrometeorological Data in China and Spatio-Temporal Analysis of FA O -56 Crop Reference Evapotranspiration and Pan Evaporation with Reference to Cli m ate Change, CSIRO Land and Water Technical Report 8/05[M]. Canberra: CSIRO Land and Water, 2005: 72-82, 96-103. http://www.clw.csiro.au/publications/technical2005/tr8-05.pdf
|
| [20] |
阎洪. 薄板光顺样条插值与中国气候空间模拟[J]. 地理科学, 2004, 24(2): 63-169. |
| [21] |
Yan Hong, Nix H A, Hutchinson M F, et al. Spatial interpolation of monthly mean climate data for China[J]. International Journal of Climatology, 2005, 25(10): 1369-1379. DOI:10.1002/(ISSN)1097-0088 |
| [22] |
Bates D, Lindstrom M, Wahba G. Gcvpack-routines for generalized cross va lid ation[J]. Communications in Statistics B-Simulation and Computation, 1987, 16: 263-297. DOI:10.1080/03610918708812590 |
| [23] |
Hutchinson M F. ANUDEM Version 5. 2 User Guide[M]. Canberra: The Austra lia National University, Center for Resource and Environment Studies 2004: http://cres.anu.edu.au/outputs/anudem.php
|
| [24] |
Yang Q K, Tom G. Van Niel, McVicar T R, et al. Developing a digital elev at ion model using ANUDEM for the Coarse Sandy Hilly Catchments of the Loess Platea u, China. CSIRO Land and Water Technical Report 7/05[M]. Canberra: CSIRO Land and Water, 2005. http://www.clw.csiro.au/publications/technical2005/tr7-05.pdf
|
| [25] |
Bolstad P V, Swift L, Collins F, et al. Measured and predicted air temperatures at basin to regional scales in the southern Appalachian mountains[J]. Agricultural and Forest Meteorology, 1998, 91: 161-176. DOI:10.1016/S0168-1923(98)00076-8 |
 2008, Vol. 34
2008, Vol. 34