2. 河北省气象与生态环境实验室;
3. 华北电力大学
2. Hebei Province Key Lab for Meteorology and Eco-environment;
3. North China Electric Power University
电力负荷预测是电力调度、用电、计划、规划等管理部门的重要工作之一。影响负荷的因素很多,气象因子的影响是其中之一,对此做一研究,对提高负荷预测技术水平、更合理地进行用电管理、安排电网运行方式和机组检修计划,提高电力系统的经济效益和社会效益都是很有益的[1-3]。
众多研究者提出了许多短期负荷预测方法,如时间序列法、专家系统、人工神经网络法等,这些方法各有自己的优点,但由于负荷变化的影响因素多且过程复杂,它们都存在一定的缺陷性和局限性。时间序列法计算量小、速度较快,但预测精度不能保证满足工程需要,且不具备自适应学习能力,预测系统的鲁棒性没有保障[4]。专家系统可以避开复杂的数值计算,但通用性较差,缺乏学习能力[5-6]。人工神经网络具有很强的鲁棒性、记忆能力、非线性映射能力以及强大的自学习能力,但收敛速度慢和可能收敛到局部最小点,且知识表达困难,难以充分利用调度人员经验中的知识[7-8]。
决策树(Decision Tree)[9-12]学习是以实例为基础的归纳学习算法,它着眼于从一组无次序、无规则的事例中推理出决策树表示形式的分类规则。利用决策树技术对气象因子和日电力负荷进行联合建模,通过训练历史数据,量化气象因子对电力负荷预测的影响,然后通过生成的预测决策树模型对历史数据进行检验、对未来数据进行预测,通过对预测值与真实值的对比,验证得到负荷预测的优化值。在负荷预测模型的生成中,综合考虑了气温、湿度等气象信息及节假日因素对日特征负荷的影响,不仅具有较好的预测结果,而且可以在一定程度上揭示出影响日特征负荷因素的相对重要性。
1 决策树技术及剪枝决策树方法是数据挖掘中非常有效的分类方法,用样本的属性作为结点,用属性的取值作为分支的树结构,利用信息论原理对大量样本的属性进行分析和归纳而产生的。决策树的根节点是所有样本中信息量最大的属性;树的中间结点是该结点为根的子树所包含的样本子集中信息量最大的属性;决策树的叶子结点是样本的类别值。
由于ID3算法的基础理论清晰,算法较简单,学习能力较强,能够处理大规模的学习问题,通过ID3这种决策树分类算法,采用基于信息熵定义的信息增益度量来选择内节点的测试属性。
1.1 ID3算法设S是n个数据样本的集合,将样本集划分为c个不同的类Ci (i=1,2,…,c),每个类Ci含有的样本数目为ni,则S划分为c个类的信息熵或期望信息为:
| $ {\text{E}}\left( S \right) = - \sum\limits_{i = 1}^n {{p_i}{{\log }_2}\left( {{p_i}} \right)} $ | (1) |
其中,pi为S中的样本属于第i类Ci的概率,即pi=ni/n。
Sv是S中属性A的值为v的样本子集,即Sv={s∈S|A(s)=v},选择A导致的信息熵定义为:
| $ {\text{E}}\left( {S, \mathit{A}} \right) = \sum\limits_{\upsilon \in {\text{Value}}\left( A \right)}^{} {\frac{{\left| {{S_\upsilon }} \right|}}{{\left| S \right|}}} {\text{E}}\left( {{S_\upsilon }} \right) $ | (2) |
其中,E(Sv)是将Sv中的样本划分到各个类的信息熵。属性A相对样本集合S的信息增益Gain(S,A)定义为:
| $ {\text{Gain}}\left( {S, A} \right) = {\text{E}}\left( S \right) - {\text{E}}\left( {S, A} \right) $ | (3) |
Gain(S,A)是指因知道属性A的值后导致的熵的期望压缩。Gain(S,A)越大,说明选择测试属性A对分类提供的信息越多。ID3算法就是在每个节点选择信息增益(S,A)最大的属性作为测试属性。
1.2 决策树的剪枝创建决策树时,由于训练样本太少或数据中存在噪音和孤立点,许多分枝反映的是训练样本集中的异常现象,建立的决策树会过度拟合训练样本集。剪枝方法可以减少训练样本集中噪音的影响,剪枝的时机选择是很关键的。
(a) 本方法中选择最小分度值为5,即扩展的叶子结点为每5个数据的汇总。
(b) 基于误差的剪枝。
本方法中利用生成的原始决策树,对每个叶子结点进行代价计算,建立差分方程,使得当斜率较为平缓时即可进行剪枝。
2 数据源原始数据中经常存在噪声数据及缺测数据,对于缺测数据当时间的跨度范围并不是很大时(n≤5天),可考虑用3次样条插值方法进行数据的插值填充;当时间跨度范围较大时只能将数据舍去。对于噪声数据可通过降噪手段(主要方法为插值、拟合)进行数据的修复,若噪声很大时则将其舍去。
系统使用Visual C# 2005作为开发平台,使用Matlab7.0做后台运算和图形显示工具,SQL Server 2005作为预测数据库。数据库中包括2004年河北省保定市每日的电力负荷,以及相应的与负荷有关的气温、湿度、降水量等气象数据,这些数据可以通过SQL Server 2000的DTS包定期加载。其中将训练集合内的负荷数据作为历史数据,训练集合外的负荷数据作为新数据。电力负荷数据中对每日96时刻1)的负荷值建立差分模型,计算出日最高电力负荷及日最低电力负荷。
1) 本文以保定地区所属的保定市区、阜平、涞源、涿州四个区域的电力负荷值作为研究样本,数据来源于SCADA系统,每天96个采本点(每15分钟一个点)。整点时刻一共24时刻,进行日24点或96点负荷预测,基本能够满足负荷预测的需要。
3 决策树负荷预测模型的实现以河北省保定市2004年1月到2004年12月的气象资料通过决策树技术建模。将日气象数据中的各种气象因子分别作为属性值,构造分类决策树,包括月份、日期、气压、温度、水汽压、降水、相对湿度、云量、蒸发量、地温、日照时数、平均风速、湿球温度、能见度、星期、节日类型等。
根据改进的ID3算法输出节点表(如表 1所示),将表中“节点”字段通过“连接”字段与“父节点”字段连接起来,形成负荷预测决策树,图 1为以文本形式表示的最高值负荷预测决策树。
|
|
表 1 改进ID3算法输出表结构 |

|
图 1 部分最高值负荷预测决策树图 |
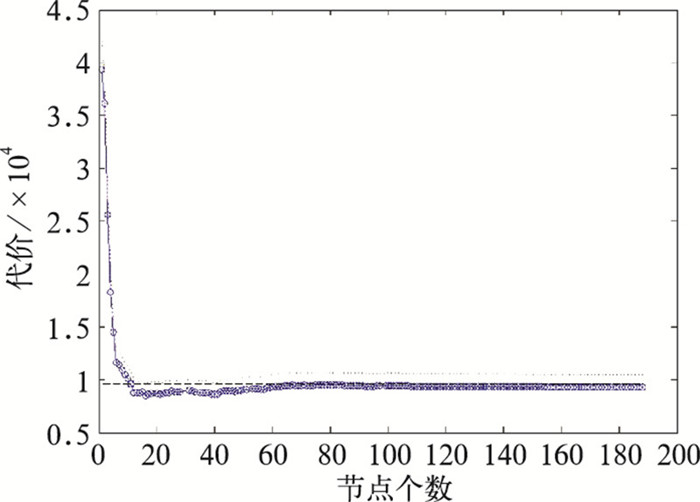
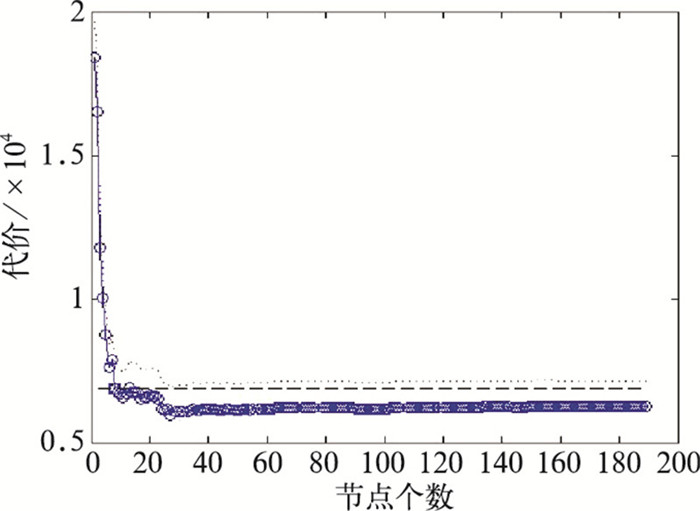
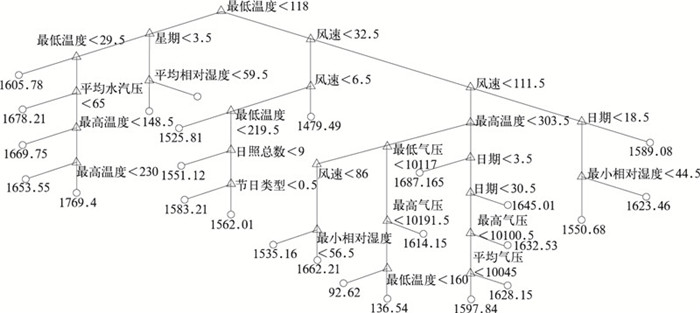
决策树中的叶子结点即为在其父节点属性条件下的负荷值。通过将训练的气象数据带入生成的决策树得到预测的负荷值,并将随着决策树叶子结点规模扩展得到的真实值与预测值的误差平方和的序列作图得到“决策树规模——代价(误差平方和)”的决策树评价图(图 2、图 3)。可以看出,当决策树仅有一个结点时,其代价最大。随着叶子结点规模的扩大,决策树代价也在不断减小。当叶子结点规模即决策树的规模达到一定程度时,决策树代价的减少率趋于缓和,利用差分方程将拐点前的结点信息分离提取即可得到最终相关的多个因子的优化决策树(图 4):
|
图 2 全因子日负荷最高值决策树评价图 |
|
图 3 全因子日负荷最低值决策树评价图 |
|
图 4 多个气象因子的日负荷最高值决策树 |
利用决策树技术对多组不同训练及生成决策树并进行历史数据预测得到结果如表 2。
|
|
表 2 优化决策树历史数据预测结果 |
利用决策树技术对多组不同训练及生成决策树并进行新数据预测得到结果如表 3。
|
|
表 3 优化决策树新数据预测结果 |
(1) 历史负荷预测检验
通过模型建立,负荷预测值的平均相对误差≤3.502%,最高负荷平均相对误差≤5.005%,最低负荷平均相对误差≤1.249%。
(2) 未来负荷预测检验
训练集外的新负荷预测值得平均相对误差≤5.108%,最高负荷平均相对误差≤5.712%,最低负荷平均相对误差≤3.172%。
通过对模型的检验可知,预测结果的精度较高,达到工业技术要求。
(3) 决策树预测历史数据较预测新数据有更高的精度,对保定2004年1月至2004年12月的最大、最小及平均负荷进行预测,则一年平均最大值预测精度可达94.3%,平均值预测精度可达94.86%,最小值预测精度达到96.7%。而且预测短时间范围的数据较预测长时间范围数据有更高的精确度。用优化决策树预测负荷时,应尽量采用附近时期的1~2个月的训练集来预测短时间(7天)范围的数据可获得较好的效果。
5 结论气象因子与负荷有着密切的关系,通过对多组训练集生成决策树的预测值与真实值的比较可知,气象类的8个因子(月份、日期、最高气温、最低温度、平均水汽压、平均风速、星期、节日类型)对电力负荷具有较高并且较稳定的量化影响,用这8个气象因子来对短期日电力负荷的最高最低值进行预测得到的结果具有较高的精确度。其中,将所有气象属性都处理为基值和变化值[4]。月份、日期、星期、节日类型等属性可直接实现,其余的气象因子通过该算法进行模型训练,形成24个或96个预测模型,则可进行日24点或96点负荷预测。
决策树算法可以揭示分类属性对决策属性的相对重要性。作为决策树算法的一种,从ID3算法生成的负荷预测决策树中我们还可以观察到:气温和气温变化值对所在地区的日最大、最小负荷变化率具有相对较大的影响,而湿度、湿度变化值及星期因素对负荷最大、最小变化率的影响相对较弱;对日平均负荷变化率影响较大的则有气温、星期和气温变化率因素。总体看来,气温及其变化值对负荷影响较大,而湿度及其变化值对负荷影响较小。
| [1] |
牛东晓. 电力负荷预测技术及其应用[M]. 北京: 中国电力出版社.
|
| [2] |
胡江林, 陈正洪, 洪斌, 等. 华中电网日负荷与气象因子的关系[J]. 气象, 28(3): 14-18. |
| [3] |
Yang Hongtzer, Huang Chao-Ming. A New Short-Term Load Forecasting Approach Using Self-Organizing Fuzzy ARMAX Models[J]. IEEE PWRS, 1998, 13(1): 464-473. |
| [4] |
RahmanS, BhatnagarR. An Expert System Base Algorithm for Short-Term Load Forecasting[J]. IEEE PWRS, 1998, 3(2). |
| [5] |
Hok-L, HsuYY, LeeCE, et al. Short-Term Load Forecasting of TaiWan Power System Using a Knowledge-Based Expert System[J]. IEEE PWRS, 1990, 5(4). |
| [6] |
Peng T M, Hubele N F, Karady G G. Advancement in the Application of Neural Networks for Short-Term Load Forecasting[J]. IEEE PWRS, 1992, 7(1): 427-435. |
| [7] |
HoK-L. Short-Term Load Forecasting Using Multi-Layer Neural Network with an Adaptive Learning Algorithm[J]. IEEE PWRS, 1992, 7(1). |
| [8] |
Quinlan J R. Induction of decision trees[J]. Machine Learning, 1986(1): 81-106. |
| [9] |
李雄飞, 李军. 数据挖掘与知识发现[M]. 北京: 高等教育出版社, 2003.
|
| [10] |
朱六璋, 袁林, 黄太贵. 短期负荷预测的实用数据挖掘模型[J]. 电力系统自动化, 2004, 28(3): 49-52. |
| [11] |
汪峰, 于尔铿. 基于因素影响的电力系统短期负荷预报方法的研究[J]. 中国电机工程学报, 1999, 19(8): 54-57. |
| [12] |
Ying-Hwa Kuo, Donall, Shapiro M A. Feasibility of short-range numerical weather prediction using observations from a network of profilers[J]. Mon.Wea.Rev, 1987, 115: 2402-2427. DOI:10.1175/1520-0493(1987)115<2402:FOSRNW>2.0.CO;2 |
 2008, Vol. 34
2008, Vol. 34