我国是受台风灾害影响较重的国家之一,一个科学、准确、客观的台风灾害影响评估模型对防灾减灾和救灾工作十分重要。为此,国内很多学者对此做了相关研究,陈舜华等[1]利用经济计量模式对台风灾情进行评估,林继生等则用多项式拟合的客观分析法定量评估灾害损失[2],李春梅等将层次分析法和专家打分法应用于广东省热带气旋灾害影响评估模式中[3],梁必骐等应用模糊数学方法建立了灾害评估模型[4] 。这些研究中多数考虑了台风的风、雨、地理信息等因素,但较少考虑承载体的影响时间、防灾减灾能力、地质特征、天文大潮等影响因子,且准确率不够高,至今还没有一个较好的全国性台风灾情评估模型。鉴于模糊数学在目标不明确的多目标综合评估中取得了很多很有意义的成果[5],本文采用模糊数学方法建立评估模型,加入台风影响时间、致灾因子、孕灾环境、防灾减灾等10个灾情影响因子,利用加权平均规划法得到影响因子的权重,对台风灾情进行定量评估,得到较理想的结果。在模型中,只要获得台风预报或观测实况资料,即可进行灾前预评估,以及灾中和灾后的快速评估,从而给相关部门提前采取相应防范措施,做好台风的防灾减灾工作提供科学定量的决策依据。
1 计算方法设有n件事物的某一特征等待评价,这n件事物构成对象集Χ和影响因子集U:
| $ \begin{array}{l} \boldsymbol{X} = \left\{ {{x_1}, {x_2}, \cdots , \left. {{x_n}} \right\}} \right.\\ \boldsymbol{U} = \left\{ {{u_1}, {u_2}, \cdots , \left. {{u_m}} \right\}} \right. \end{array} $ |
对因子的权重分配为U上的模糊子集W,记为:
| $ \boldsymbol{W} = \left\{ {{\omega _1}, {\omega _2}, \cdots , \left. {{\omega _m}} \right\}} \right., 其中{\omega _i} \ge 0, i = 1, 2, \cdots , m. $ |
式中:m表示影响因子的个数,ωi表示第i个因子ui所对应的权重。
n件事物中每个因子的评价集为Ri=(ri1, ri2, …, rin), i=1, 2, …, m, 则有m个影响因子得到的评价矩阵为:
| $ \boldsymbol{R} = \left[ {\begin{array}{*{20}{c}} {{r_{11}}}&{{r_{12}}}& \cdots &{{r_{1n}}}\\ {{r_{21}}}&{{r_{22}}}& \cdots &{{r_{2n}}}\\ \cdots&\cdots&\cdots&\cdots \\ {{r_{m1}}}&{{r_{m2}}}& \cdots &{{r_{mn}}} \end{array}} \right] $ |
则对该评价对象的模糊综合评价集B为:
| $ \underline B = \underline {W\bigcirc R} $ | (1) |
B就是n件事物的模糊综合评价系数集,系数越大表示灾害程度越严重。在这里,“○”为广义模糊算子,其算法有多种模型,我们采用加权平均型模型M(^·, +),即
隶属函数在模糊数学中具有重要的地位,在解决某一实际问题时,一般先要确定隶属函数。模糊集是研究和处理客观世界中存在的模糊现象的,一般用隶属函数来刻画,从而实现定量地描述模糊性事物。隶属函数经常需要在一些控制实验的基础上获得,它的确定在一定程度上具有主观性和经验性。确定隶属函数的方法一般有模糊统计法、典型函数法等。我们采用典型函数法的戒下型函数[6],表达式如下:
| $ f\left( u \right) = \left\{ {\begin{array}{*{20}{l}} 0&{\left( {u \le c} \right)}\\ {\frac{1}{{1 + {{\left[ {a\left( {u - c} \right)} \right]}^{ - b}}}}}&{\left( {u > c} \right)} \end{array}} \right. $ | (2) |
其中,f(u)为因子u的隶属函数,a、b、c均为参数,且a>0,b>0,c>0。
从这种戒下型函数的表达式来看,可以表示台风灾害的大小程度。当影响因子u的值大于某一界值时(界值为c,表示因子u的最小值),认为可以成灾,否则不成灾。灾情因子统计数据U的增大,表示灾情轻重的隶属函数值f(u)也会增大。
2.2 参数的确定在式(2)中,规定b=2;c=umin,为因子u的统计最小值;a的确定如下:
令u的统计最大值为umax,所对应隶属函数的值(隶属度)为0.99,则有:
| $ \begin{array}{l} 0.99 = \frac{1}{{1 + {{\left[ {a\left( {{u_{\max }} - c} \right)} \right]}^{ - 2}}}}\\ 得到a = \frac{{\sqrt {99} }}{{{u_{\max }} - {u_{\min }}}} \end{array} $ |
在实际计算时,a值偏大。为使a值能够有利于隶属度的计算,因此我们定义一个经验系数K,经多次试验计算,取K为0.3较为合适。因此得到:
| $ a = \frac{{\sqrt {99} }}{{{u_{\max }} - {u_{\min }}}} \times K $ | (3) |
a、b、c确定后,可利用灾情隶属度公式(2)求出每个登陆台风的各灾情因子隶属度值, 构成矩阵R。
| $ \boldsymbol{R} = \left[ {\begin{array}{*{20}{c}} {{f_{11}}}&{{f_{12}}}& \cdots &{{f_{1n}}}\\ {{f_{21}}}&{{f_{22}}}& \cdots &{{f_{2n}}}\\ \cdots&\cdots&\cdots&\cdots \\ {{f_{m1}}}&{{f_{m2}}}& \cdots &{{f_{mn}}} \end{array}} \right] $ |
模糊综合评价中权重系数的大小反映了各参评因子的相对重要程度,取值的好坏将直接影响到评价结果的好坏。常用的定权方法有:专家咨询法、调查统计法、相关分析法等,但这些方法要么过多地依赖人的主观判断和经验,难以让人信服;要么是建立在统计的基础上,但统计数据的收集和选择比较困难。因此,为客观、准确地确定权重值,文献[5]利用加权平均规划法得到的权重计算在实际应用中效果不错。建立如下多目标决策模型为:
| $ \begin{array}{l} \;\;\;\;\max \left\{ {b(\omega ) = ({b_1}(\omega ),({b_2}(\omega ), \cdots } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{(}}{b_n}(\omega ))\mid \sum\limits_{i = 1}^p {{\omega ^2}} = \left. c \right\}\\ 其中,d = 1 - \sum\limits_{i = p = 1}^m \omega ,c = 1 - \sum\limits_{i = p = 1}^m {{\omega ^2}} \end{array} $ |
p为目标权重是待定的因子数,d为待定因子的权重之和。当所有因子的权重都未知时,p=m,d=1。将多目标决策问题等权重集结为等价的非线性规划问题后,解得权重的表达式为:
| $ {\omega _i} = d\sum\limits_{j = 1}^n {{r_{ij}}/\sum\limits_{i = 1}^p {} } \sum\limits_{j = 1}^n {{r_{ij}}}\;\;\;\;\;\;{\rm{ }}i = 1, 2, \cdots , p. $ | (4) |
从权重计算表达式可以看出,权重与参与计算的所有个例和因子都有关,这样,同一个例在参与不同的个例计算中,权重不固定,评价系数也不固定,因此就无法用评价系数划分等级。选择较多的历史个例,利用式(4)全部计算权重或部分确定权重,对应计算出相应的评估系数,选择评价系数分级与实际灾害损失对应较好的一组权重固定下来,即可在以后的计算中直接使用。
2.4 评价系数的计算总的评价矩阵R和影响因子权重集W通过上述确定后,由式(1)计算可得n件事物的模糊综合评价系数集B。bj就是每个登陆台风灾情的综合评价指数。
3 登陆台风的模糊综合评价实例 3.1 登陆热带气旋个例的选取考虑到社会经济发展、地方抗灾能力等因素的变化,取经济发展与当前较接近的2000—2006年资料进行计算。本文在41个登陆中国大陆的热带气旋中选择了40个,剔除掉1个在琼州海峡反复登陆的台风。热带气旋资料取自气象出版社出版的《台风年鉴》,热带气旋造成的直接经济损失根据国家气象中心的统计结果。
3.2 影响因子的选取台风灾害的主要类型有暴雨灾害、狂风灾害、次生灾害(滑坡、泥石流等)、风暴潮灾害等。此外,考虑到全国各地区的经济发展不平衡,人口密度也相差较大,同样强度和时空尺度的台风在不同的地区造成的灾害和影响相差会很大,我们将地区易损性也作为一个影响因子(以省区市为单位)。这样,我们选取10个因子放入模型中进行计算,即A1:过程最大雨量、A2:24小时最大雨量、A3:登陆时最大风速、A4:登陆时最低气压、A5:登陆后持续时间(小时)、A6:影响范围(50mm以上降水和6级以上大风影响的省)、A7:影响区域的易损性、A8:影响区域的地质灾害危险性、A9:登陆时的天文大潮指数、A10:影响区域的防灾能力指数。
3.3 处理方法过程最大雨量、24小时最大雨量、登陆时最大风速、最低气压均直接使用观测或预报值;持续时间为登陆到停编的时间;影响范围以省为单位;地区易损性和地质灾害危险性直接采用文献[7]的数据,防灾能力引用文献[8]中各风险区的工程防御能力指标。其中,易损性为经济易损指标值和社会易损指标值的均方根值,易损性、防御能力和地质灾害危险性三个影响因子的取值分别为过程50mm雨区覆盖区域(以省为单位)相应指标的平均值;天文大潮的处理为登陆时遇阴历初一、初二、初三或十五、十六、十七时考虑,否则不予考虑。
3.4 灾害影响评估等级划分由于台风造成的人员伤亡具有极大的偶然性,气象因子对死亡人数影响的显著性较低[8],本文主要依据登陆台风造成的直接经济损失进行分级。考虑物价变动因素,将与生活相关较高的居民消费指数近似作为年物价上升指数,对各个年份自然灾害的损失值归一到指定的作为比较基准的年份计算灾害可比损失值,得出社会物质价值损失的绝对值[9],其数学表达式为:
可比经济损失值=∑实际经济损失值×年物价上升指数×比较期间(年)
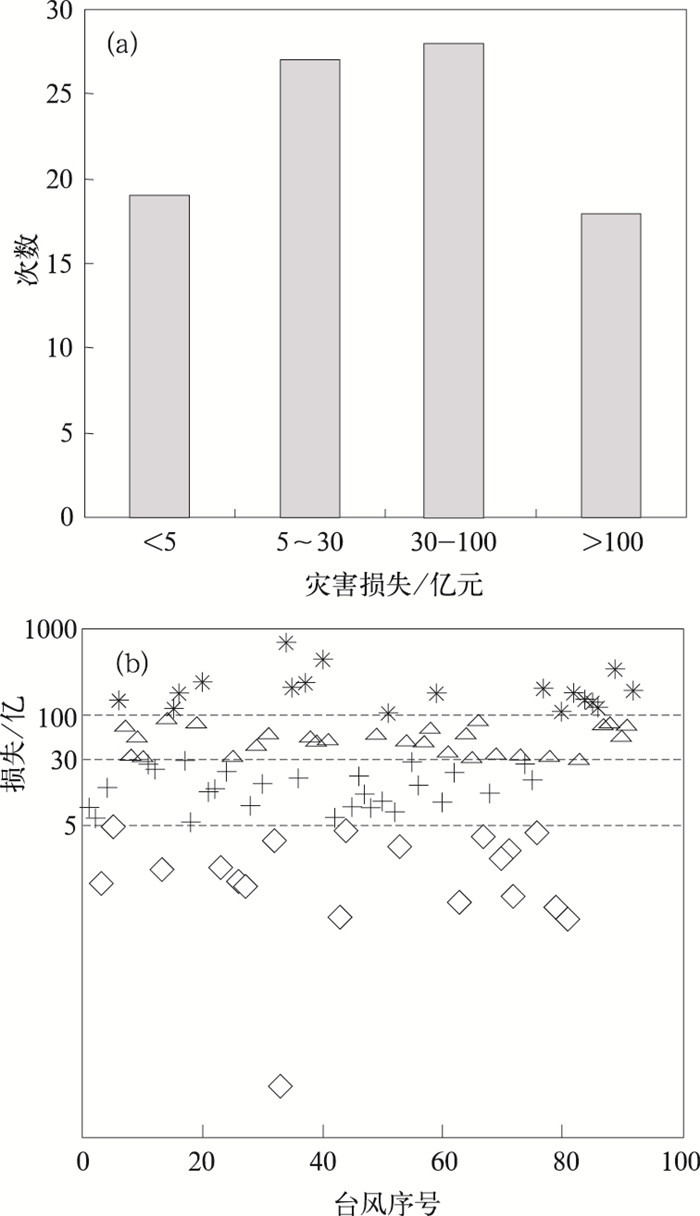
对1992—2006年间登陆我国台风(92个)造成的直接经济损失进行分析,以1992年为基准年,根据国家统计局公布的每年价格指数对可比经济损失进行换算,得到15年的灾害损失分布图,发现灾害损失在4个区域[0, 5]、[5,30)、[30,100)、[100,1000)呈现一种类正态分布(图 1,单位:亿元),同时,这样划分对防灾减灾也具有较好的参考作用,故将台风灾害影响评估等级分为相应四级,一级为特别重大(参考直接经济损失约为100亿元以上),二级为重大(参考直接经济损失约为30~100亿元),三级为较重(参考直接经济损失约为5~30亿元),四级为一般(参考直接经济损失约为5亿元以下)。分析2000—2006年的登陆台风的综合评价系数,发现综合评价系数可依据灾害影响评估等级分为相应四级,且具有较好的一致性。评估等级与综合评价系数的对应关系如下:
|
图 1 1992—2006年登陆我国台风造成的经济损失分布图 |
1级 bj≥0.6灾情损失特别重大
2级 0.54≤bj<0.6灾情损失重大
3级 0.46≤bj<0.54灾情损失较重
4级 bj<0.46灾情损失一般
3.5 结果分析利用模糊数学建立的热带气旋灾情评估模型,对2000—2006年登陆我国的台风灾情损失进行评估,结果表明(表 2):评估等级与实际的灾情级别均很接近,与实际灾情程度较为一致,同时,利用加权平均规划法计算出的10个影响因子(A1~A10)的权重依次为:0.11812、0.12627、0.12261、0.13396、0.09476、0.10652、0.11607 7、0.05046、0.03266、0.09856,模型计算出的各因子权重大小也反映出各因子对实际灾情的影响程度,表明该模型能够较好地评估登陆热带气旋造成的灾情。
|
|
表 2 2000—2006年登陆我国台风个例的灾情指数 |
在这40个台风中,各个灾害等级的台风,评估等级与实际的灾情级别均很接近,较好地反映出灾情的轻重(图 2)。灾情等级为特别重大(1级)、重大(2级)、较重(3级)、一般(4级)的准确率Ts评分分别为89%、87%、73%、78%,全部个例的拟合率达到90%。模型评估中等级空报、漏报的级别也仅差1级。这些都表明模型能够较好地评估登陆热带气旋造成的灾情。

|
图 2 2000—2006年登陆我国台风的灾害评估指数与实际经济损失的相关图 |
应用模糊综合评价法对登陆我国的台风灾害影响进行评估试验,遴选10个因子作为灾害的影响因子,利用加权平均规划法确定影响因子的权重。对2000—2006年登陆台风的影响评估进行试验,评估等级与实际的灾情级别均很接近,与实际灾情程度较为一致,说明该模型能较好地评估我国登陆台风造成的灾情。
由于台风致灾因子均可在灾前得到预测值,所以又具有一定的预测效果。实际灾情的严重程度,除本文所选的因子,还与预报正确率的提高、防灾减灾能力的增强、以及采取的减灾措施有关。我们目前进行的台风灾情评估工作,虽取得一定的效果,但还需要对更多的实例进行评估检验,进一步考虑社会、经济影响等带来的变化,重点对影响区域的脆弱性以及防灾减灾能力进行订正,以选出最适合的台风影响因子权重,运用到今后的业务工作中,提供相关部门快速、较准确的灾前预评估、灾中跟踪评估和灾后评估产品,为防灾减灾和救灾工作提供依据。
| [1] |
陈舜华, 吕纯濂, 李吉顺. 福建台风灾害评估试验[J]. 中国减灾, 1994, 4(3): 31-34. |
| [2] |
林继生, 罗金玲. 登陆广东的热带气旋灾害评估和预测模式[J]. 自然灾害学报, 1995, 1: 92-97. |
| [3] |
李春梅, 罗晓玲, 刘锦銮, 等. 层次分析法在热带气旋灾害影响评估模式中的应用[J]. 热带气象学报, 2000, 6: 224-228. |
| [4] |
梁必骐, 樊琦, 杨洁, 等. 热带气旋灾害的模糊数学评价[J]. 热带气象学报, 1999, 15(4): 305-311. |
| [5] |
李登峰, 程春田, 陈守煜. 部分信息不完全的多目标决策方法[J]. 控制与决策, 1998, 13(1): 83-86. |
| [6] |
周浩亮. 模糊数学基本理论及其应用[J]. 建井技术, 1994(21): 70-80. |
| [7] |
刘丽, 代宏霞. 中国自然灾害保险风险度综合评判与区划[J]. 山地学报, 2004, 22(4): 477-482. |
| [8] |
国家科委, 国家纪委, 国家经贸委自然灾害综合研究组. 中国自然灾害区划研究进展[M]. 北京: 海洋出版社, 1998: 76-149.
|
| [9] |
赵阿兴, 马宗晋. 自然灾害损失指标体系的研究[J]. 自然灾害学报, 1993, 7: 1-7. |
| [10] |
彭祖赠, 孙韫玉. 模糊数学及其应用[M]. 武汉: 武汉大学出版社, 2002: 1-47.
|
| [11] |
樊琦, 梁必骐. 热带气旋灾害经济损失的模糊数学评测[J]. 气象科学, 2000, 2: 360-366. DOI:10.3969/j.issn.1009-0827.2000.03.016 |
| [12] |
刘玉函, 唐春哓, 宋丽莉. 广东台风灾情评估探讨[J]. 热带地理, 2003, 6: 119-122. DOI:10.3969/j.issn.1001-5221.2003.02.006 |
| [13] |
冯利华. 灾害损失的定量计算[J]. 灾害学, 1993, 5: 17-19. |
 2008, Vol. 34
2008, Vol. 34