2. 湖北省气象科技服务中心
2. Meteorological Science Service Center of Hubei Province
气温是影响电力指标波动的最主要环境因素,特别是在全球变暖的背景下,高温热浪、暖日、暖夜、气温剧烈变化等发生频率加大,这种影响将会加剧。为了科学合理的电力调度,一些气象工作者配合电力部门,开展了电力指标与多项气象因子的相关性分析、评估和预测模型的研究。陈正洪、洪国平、张小玲等[1-4]分别分析了华中电网和武汉市的日(周)电量、最大负荷、北京市夏季用电与气温的相关性,并通过分月计算得出不同月份1℃效应量,并分季建立了电力指标与气温间的线性评估模型。李雪铭、赵彤等利用逐步回归、多元回归建立了气温变化与城市居民电量变化模型[5-8],胡江林等[9-10]则通过消去社会趋势项、节假日的影响,得到华中电网日电量和最大负荷的波动量(气象电量或负荷),发现电力指标以18℃左右为临界值,在高气温的情况下,气温上升,电力指标上升,低气温的情况下,气温下降,电力指标上升,并建立了华中电网负荷的动态混合线性回归、人工神经网络方法预测模型。
以上工作大部分采用线性模型,并且将时间、温度按一定的条件分段。人工神经网络预测模型则通过其自学习功能,训练得到变量的非线性关系。本研究则以武汉市为例,采用非线性模型(二次曲线),以更准确、全面地评估气温对周年逐日电量、最大负荷、最小负荷的定量影响,拟合程度高,物理意义明确,得到了一些有用的结论,并在2008年1月严重冰雪冻害来临时,投入准业务应用。
1 资料与方法 1.1 资料获得了武汉市2005年1月1日至2007年9日30日逐日电量、最大负荷、最小负荷(分别有1003个有效样本)及同期日平均气温、日最高气温、日最低气温资料。
研究表明,春节期间负荷与其他时间相比可小30%[9],故本研究不考虑春节期间资料(包括春节7天及春节前2天)。
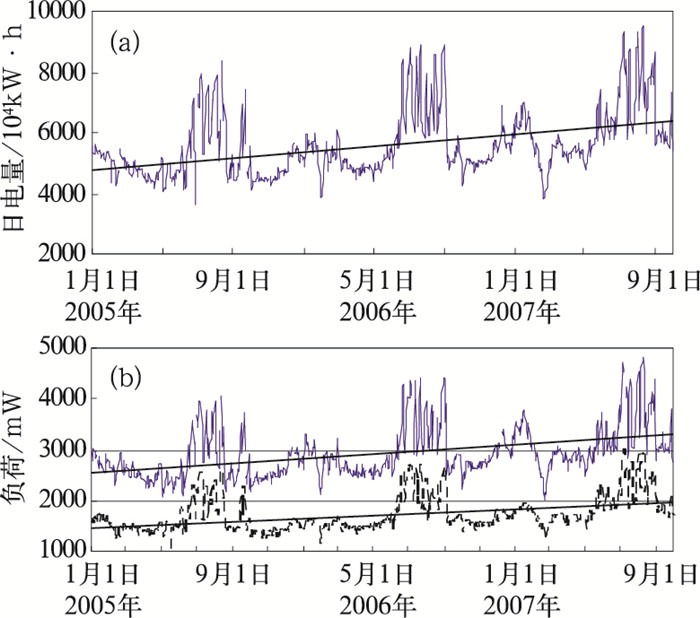
图 1为2005年1月1日至2007年9日30日武汉市逐日电量、最大负荷、最小负荷随时间的变化。从图 1可见,无论哪个指标都包含三项变化,即长期增长趋势、季节波动以及逐日变化,分别对应着社会经济发展、气温季节变化、气象要素(主要是气温)变化对供电指标的影响。
|
图 1 各电力指标随时间的变化(2005年1月1日至2007年9日30日,直线为趋势项) (a)日电量(b)日最大负荷(实线)、最小负荷(虚线) |
由于2005—2007年间武汉市经济增长和电器增加速度比较均匀,可采用线性关系来表示国民经济增长和电器增加引起的三项电力因子长期增长趋势项:
| $ i(t) = {a_1}t + {b_1} $ | (1) |
| $ l(t) = {a_2}t + {b_2} $ | (2) |
| $ s(t) = {a_3}t + {b_3} $ | (3) |
以逐日资料减去日趋势项,便可反映季节变化和气温逐日变化对电力指标的影响,即:
| $ {Y_{i\left( t \right)}} = {I_{实\left( t \right)}} - {i_{\left( t \right)}} $ | (4) |
| $ {Y_{l\left( t \right)}} = {L_{实\left( t \right)}} - {l_{\left( t \right)}} $ | (5) |
| $ {Y_{s\left( t \right)}} = {S_{实\left( t \right)}} - {s_{\left( t \right)}} $ | (6) |
其中,i(t)、l(t)、s(t)分别为日电量、最大负荷、最小负荷的增长趋势项;Yi(t)、Yl(t)、Ys(t)分别为逐日波动日电量、波动最大负荷、波动最小负荷;I实(t)、L实(t)、S实(t)分别为逐日实际电量、最大负荷、最小负荷;t为日序数,2005年1月1日为1,2005年1月2日为2,……。
1.2 方法以武汉市2005—2006年逐日波动日电量、最大负荷、最小负荷资料与同期日平均气温、最高气温、最低气温为基础,建立电力指标与气温的非线性模型。非线性模型有多种,以二次多项式(抛物线型)效果最理想。求取每1℃间隔的1℃电力指标效应量,并将拟合模型的复相关系数与分冬夏半年的线性相关系数比较。以2007年1—9月各电力因子资料与波动日电量、最大负荷、最小负荷资料的计算值进行相关分析,同时利用2007年1—9月个各电力因子计算值(趋势项与波动量计算值的和)与实际值进行相对误差分析。
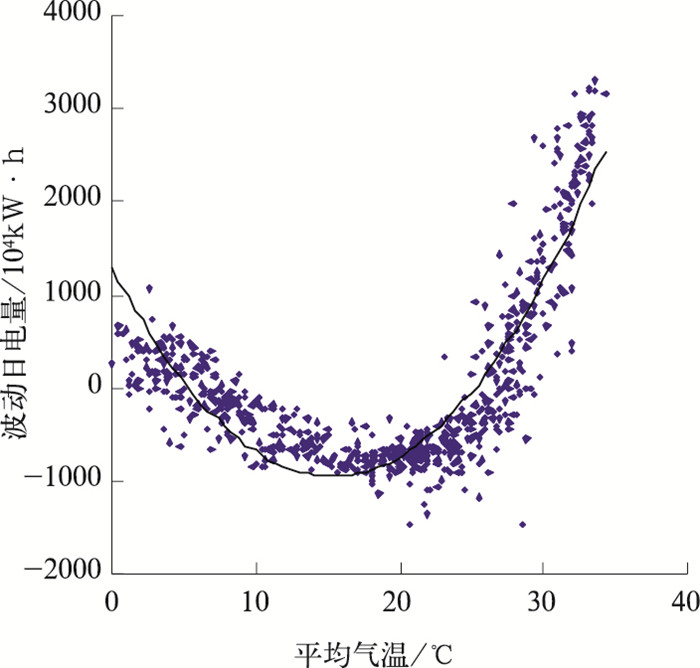
2 结果分析 2.1 模型的建立绘制武汉市2005—2006年波动日电量、最大负荷、最小负荷(Yi(x)、Yl(x)、Ys(x))与同期日平均气温、最高气温、最低气温的关系曲线。图 2为波动日电量与日平均气温分布图和模拟曲线。
|
图 2 武汉市波动日电量与日平均气温的拟合曲线 2005年1月1日—2006年12月31日 |
分析表明:(1)三项电力指标分别与三项气温均呈向上开口的抛物线关系,说明存在一个最小值,也就是在其附近电力指标对气温变化不敏感,同时只要气温大于(小于)该值,气温越高(低),对电力指标影响就越大;(2)三项电力指标与平均气温、最低气温关系较好,与最高气温的拟合相对稍差,由于日最低气温往往出现在凌晨或夜间,表明电量及负荷的逐日波动与日平均气温及夜间的温度关系最为密切。表 1列出了各电力指标与三项气温的非线性关系式,所有方程的相关系数都在0.8以上,最高达0.89。
|
|
表 1 温度与波动日电量、最大负荷、最小负荷拟合方程 |
由于电力指标与气温是曲线关系,即不同阶段气温的变化造成的电量或负荷变化量是不同的,利用表 1的曲线方程,就可以很方便地计算出日平均气温每增加1℃造成的日电量、最大负荷、最小负荷的变化量,也就是1℃效应量,并列于表 2。
|
|
表 2 不同平均气温下日电量、最大负荷、最小负荷的1℃效应量 |
由表 2可见,当日平均气温在13~16℃时,气温对电量及最大负荷的影响是较小的,其中,当日平均气温在14~15℃,对电量影响是最小的,而最大、最小负荷的不敏感温度分别为15~16℃、13~14℃。当日平均气温在3~0℃,每下降1℃,日电量将升高228~287(104kW·h),最大负荷增加109~136MW,而日平均气温在31~34℃,每升高1℃,日电量将上升315~374(104kW·h),最大负荷上升142~169 MW。
在计算1℃效应量的同时,对最低气温不同阶段变化对电量的影响也进行了分析,结果表明,日电量对最低气温最不敏感的区域是11~12℃(表略),当最低气温在零下3~6℃时,每下降1℃,日电量增加286~345(104kW·h)。
2.3 与线性相关的比较由于线性模型无法很好地模拟出图 2的趋势,但可进行分段相关分析,将2005年1月1日—200 6年12月31日的资料按冬夏两个半年分类,夏半年为4—9月,冬半年为10月至次年的3月,结果如表 3。
|
|
表 3 冬、夏半年电力指标与气温的单相关系数 |
从表 3可以看出,电力指标在夏半年与气温呈正相关,冬半年呈负相关,就相关系数的绝对值来说,冬半年各气温值与波动电量、最大负荷的关系比夏季好,冬半年波动电量、波动最大负荷与各气温值的相关系数绝对值都超过0.8。虽然在进行分段处理后,能看出不同的季节电力因子与温度的对应关系,并有较高的相关性,但电力因子与气温变化响应的连续性规律、极值点以及连续变化的1℃效应量都无法准确的表示出来(线性关系的1℃效应量是通过分月统计求得,并不连续)。
2.4 效果检验根据表 1的方程,利用2007年1—9月逐日气温资料计算出逐日三项电力波动指标,并与实际日电量、最大负荷、最小负荷资料进行相关分析和精度检验。
(1) 相关分析
日电量与波动日电量的相关系数为0.91,日最大负荷与波动日最大负荷的相关系数为0. 92,日最小负荷与波动日最小负荷的相关系数为0.87,结果均通过0.01显著性水平检验。
(2) 精度检验
利用趋势项与波动量的计算值之和作为电力指标的计算值,与2007年各电力指标实际值进行比较,日电量、最大负荷、最小负荷的平均相对误差分别为5.6%、5%、6.8%。
由于影响电力因子的除气象因子外,还受诸多因子的影响,如周末、节假日,如果将这些因子的影响都引入模型,其模拟精度会进一步上升。
3 结论(1) 电力指标都存在三项变化,即长期增长趋势、季节波动以及逐日变化,分别对应着社会经济发展、气温季节变化、气象要素(主要是气温)逐日变化对供电指标的影响。
(2) 波动电力指标与气温呈非线性,为二次曲线(抛物线)关系。说明存在一个气温临界值,在其附近电力指标对气温变化不敏感,一旦气温大于(小于)该值,气温越高(低),对电力指标影响就越大;日平均气温的临界值为14~15℃;电力指标的1℃效应量不是固定不变的,而是随气温变化而变化的。
(3) 电力指标的波动量与日平均气温及日最低气温的关系最为密切。
(4) 经过多种方法检验,非线性模型(抛物线型)模拟效果较理想,可以推广应用。
| [1] |
陈正洪, 洪斌. 周平均"日电量—气温"关系评估及预测模型研究[J]. 华中电力, 2000, 13(1): 26-28. |
| [2] |
陈正洪, 魏静. 武汉市供电量及其最大负荷的气象预报方法[J]. 湖北气象, 2000(3): 24-28. |
| [3] |
洪国平, 李银娥, 孙新德, 等. 武汉市电网电量、电力负荷与气温的关系及预测模型研究[J]. 华中电力, 2006, l9(2): 4-7. |
| [4] |
张小玲, 王迎春. 北京夏季用电量与气象条件的关系及预报[J]. 气象, 2002, 28(2): 17-21. DOI:10.7519/j.issn.1000-0526.2002.02.004 |
| [5] |
李雪铭, 葛庆龙, 周连义, 等. 近二十年全球气温变化的居民电量响应[J]. 干旱区资源与环境, 2003, 17(5): 54-58. |
| [6] |
李继红, 张锋. 气温对浙江电网电量影响的研究[J]. 华东电力, 2005, 33(11): 39-42. DOI:10.3969/j.issn.1001-9529.2005.11.011 |
| [7] |
赵彤, 孙大雁, 葛诚, 等. 江苏电网夏季气温与电量敏感性关系初探[J]. 电力需求侧管理, 2004, 6(6): 20-26. |
| [8] |
田白, 林铍德, 雷桂莲. 气象因子对夏季电力负荷影响的分析[J]. 南昌航空工业学院学报(自然科学版), 2005, 19(1): 86-89. |
| [9] |
胡江林, 陈正洪, 洪斌. 华中电网日负荷与气象因子的关系[J]. 气象, 2002, 28(3): 14-18. DOI:10.7519/j.issn.1000-0526.2002.03.003 |
| [10] |
胡江林, 陈正洪, 洪斌, 等. 基于气象因子的华中电网负荷预测方法研究[J]. 应用气象学报, 2002, 13(5): 600-608. |
 2008, Vol. 34
2008, Vol. 34