2. 国家气象中心
2. National Meteorological Center
1975年8月,7503号台风在我国福建省登陆后,变为低压,深入内陆到达河南省境内,停滞近20小时[1],8月5—7日连续的强降水过程,使得淮河的支流汝河、沙颖河水位暴涨,造成河南省驻马店地区板桥、石漫滩两座大型水库,竹沟、田岗两座中型水库,58座小型水库在短短数小时内相继垮坝溃决。河南省有29个县市113×104hm2农田被淹,其中1100万人受灾,超过2.6万人死难,倒塌房屋596万间,冲走耕畜30.23万头,纵贯中国南北的京广线被冲毁102km,中断行车18天,影响运输48天,直接经济损失近百亿元[2]。
对于河南“75.8"大暴雨,我国气象工作者在1970年代后期到1980年代初期做过很多天气学和动力学的研究工作[1,3,4-5],陶诗言[1]综合分析了这次大暴雨过程,并指出了分段降水的影响系统和发生、发展和维持的条件,地形影响等,提出了暴雨天气学模型。丁一汇[3]从尺度相互作用的观点分析了暴雨发生的大尺度条件及暴雨对大尺度环境场的反馈作用,并探讨了暴雨维持的机制。赵思雄、周晓平[5]利用一个细网格的多层原始方程模式,进行了数值模拟,其结果表明:初始风场对暴雨的发生有相当大的影响,虽然模拟出的雨量和实况有较大差别,但是雨区的特征仍具有参考价值。1990年代后,由于NWP在天气预报中发挥着越来越重要的作用,蔡则怡、宇如聪[6]利用LASG-η模式对这次暴雨过程进行了数值试验,模拟结果为实况雨量中心(水文站纪录)的34%~49%。2005年,河南“75.8"大暴雨三十周年之际,在河南郑州召开了专题研讨会,在对事件的总结思考中,关于此次过程的可预报性问题研究一直都备受关注[7]。本文希望一方面用中国气象局新一代数值模式和新近发展的中尺度集合预报技术来对河南“75.8"过程的可预报性问题展开研究,为特大灾害天气过程预报准确率的提高提供参考,一方面了解模式对于这类强降水过程的捕捉能力,也尝试开展中尺度集合预报技术的一些初步探索。
集合预报技术的发展已历经40余年,从上世纪末开始,集合预报技术的应用研究领域已从气候预测、大尺度天气系统的中期预报和降水等天气过程短期预报,拓展到对各种中小尺度天气系统(小到风暴尺度、云尺度系统)的预报[8]。近期研究表明[9]:全球中期集合预报系统很难识别和预报中、小尺度系统及其伴随的极端降水过程,这就使更多研究采用有限区域中尺度模式,针对中尺度强降水天气的短期天气过程进行数值模拟研究。近十余年来,随着集合预报技术的发展,发现模式中对各种物理过程的描述,特别是次网格尺度过程的参数化,无论其表达方式,还是其中的经验性参数的取值,均隐含着不同程度的不确定性,而且模拟试验研究(Harrison[10]、Hou[11]、Arribas[12])表明:模式的不确定性对预报误差的影响不能忽略。张大林[13]、陈静[14]等研究了大气的非绝热物理参数化方案对降水的影响,认为:积云对流参数化方案对降水的影响很大。顾建峰[15]利用MM5模式中3种不同的深对流参数化方案(Anthes-Kuo方案,Grell方案和Betts方案),对华东地区27个测站进行了连续3个月和7个月的降水试验,发现不同的对流方案对预报质量的影响存在着一定的差异,且这种差异7个月比3个月明显。段旭等[16]利用MM5模式中3种不同的物理过程,进行三重嵌套,同时考虑模式的不同分辨率讨论低纬降水的预报性能,试验结果表明:预报效果是由多个物理过程共同作用的结果,对于不同的天气过程,各方案的表现并不完全相同。伍红雨等[17]利用不同的对流参数化方案和显式物理方案进行组合,对贵州降水进行敏感性试验,不同的方案对降水的预报效果存在着差别。由此可见:在数值模拟中,模式的不确定性,特别是物理过程描述的不确定性对预报效果的影响不容忽视。Lorenz在30年前就提出了显式随机参数化的方法,即把它们当作随机过程来处理(如选取一些对预报结果很敏感的参数,在合理的范围内,对它们进行随机扰动,或是对这些参数进行随机组合。Houtekamer等[18]对加拿大全球模式中不同的物理参数化方案进行随机组合以构造集合成员。Arribas[12]选取英国气象局(UKMO)的统一模式中的夹卷率系数、临界相对湿度、对流有效位能(CAPE)释放时间、临界弗罗德(Froude)数等进行随机扰动以构造集合成员。Charron[19]在加拿大的中尺度集合预报中针对积云对流参数化方案的云参数和对流激发函数进行随机扰动以构造集合成员。
此外,集合预报技术业务应用中一个需要考虑的问题是:怎样合理地利用计算机资源?这就涉及到采用多少集合成员数的问题。Epstein[20]、Houtekamer等[21]以及Du[22]都做过相关的研究,认为:用8~10个集合成员,可以得到适当精确度的最佳预报估狡(即集合平均),但对预报误差的估计可能需要更多的集合成员。Mullen and Buizza[23]用欧洲中期天气预报中心(ECMWF)的集合预报系统研究了集合成员数以及模式分辨率对降水预报的影响,他们指出,采用合适的模式分辨率来构造集合系统,其技巧性更高。如何将模式分辨率的问题与集合预报的思路联系起来?怎样在高分辨率的确定性预报和低分辨率的集合预报之间建立良好的平衡?Roebber等指出[24]:开展高分辨率的精细预报和开展集合预报各有长处,前者有助于预报员对于各种不同的中小尺度天气现象建立概念模型;后者有助于量化预报的不确定性,把两者结合起来能在最大程度上发挥预报的潜能。Mass同样指出[25]:中尺度集合预报需要分辨率相对高的模式,在有限资源的前提下,把高分辨率的模式和集合预报同时考虑这是一个不错的选择。Du[26]的想法和Mass不谋而合,提出了一种"混合分辨率"的方案,通过模式的不同分辨率来体现不同天气尺度系统预报的不确定性,用高分辨模式更多地反映中小尺度系统的特征,用几个低分辨率模式的集合系统来补充大尺度天气演变和预报可靠性的信息。
中尺度集合预报的研究虽在我国起步较晚,但是近些年的发展却迅速,科研院所和业务部门都积极开展这方面的研究。陈静[27]对美国PSU/NCAR的中尺度模式(MM5)中Grell对流参数化方案中的对流激发函数进行了扰动,结果表明:成员预报之间的离散度较小,不能很好地反映暴雨预报中的不确定性。谭燕、陈德辉[28]通过对多种物理过程的组合、显式随机扰动敏感参数、物理趋向扰动等多种方法来反映模式的不确定性,指出了模式不确定性在中尺度集合预报系统构建过程中的必要性。在研究和业务应用上,则更多的采用多种物理参数化方案的组合来构造集合成员[29-30]。
本文从积云对流参数化方案内在的不确定性入手进行集合预报试验,并尝试用不同分辨率模式和不同物理参数化方案的各种组合来研究模式不确定性对“75.8"大暴雨预报的影响。
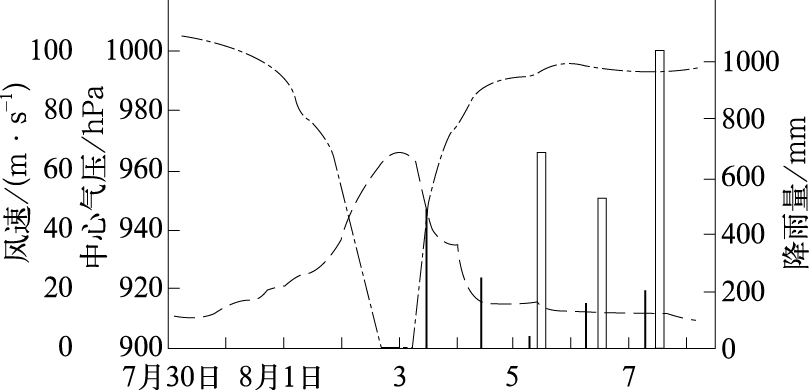
1 过程概况“75.8"大暴雨实际上由3次暴雨过程构成:由水文站观测记录可知, 5日暴雨范围较小,但强度大,最大日雨量672mm;6日暴雨范围大,但强度小,最大日降水量514mm;7日暴雨不仅范围大,且强度也大,最大日降水量达到1005mm[3]。对于“75.8"大暴雨3天的降水过程,均开展了如试验1所述的集合试验,其中8月5日的控制预报最大降水量为50mm,集合平均后为65mm,改善了约30%;8月6日的控制预报最大降水量为70mm,集合平均后为90mm,改善了约30%;8月7日的控制预报最大降水量为60mm,集合平均后为70mm,改善了约16%。从定性的角度考虑看,3天的强降水过程,集合预报的表现均优于单一的确定性预报;从定量的角度考虑看,3天的模拟结果中,6日的控制预报效果与实况最接近,集合预报的改善程度较为明显。为了便于说明问题,为后续工作的展开,故主要研究分析6日的过程。图 1给出了7503号台风中心气压、最大风速变化曲线与最大日降水量。
|
图 1 7503台风中心气压(实线)、风速(点线)变化曲线与日雨量图 垂直线为气象站雨量,空心柱为水文站雨量(引自蔡则怡[6]) |
试验采用非静力高分辨率中尺度区域模式(GRAPES-meso),模式垂直方向取σ坐标,分不等距的33层,层顶为10hPa;模式分辨率约30km,格点数为111×121,计算域中心位于河南(34.5°N、114°E), 范围大致为:18~51°N、96~132°E。控制预报的物理参数化过程选用:Kain-Fritsch Eta积云对流参数化方案、MRF边界层参数化方案、NCEP cloud3云微物理方案、Duhia辐射方案。模式变量的初始场和侧边界值使用美国国家环境预报中心(NCEP)的2.5°×2.5°经纬网格再分析场资料,侧边界变量值每6小时更新一次,选取1975年8月6日0000UTC为初始时刻,模式积分24小时,时间步长取300秒,模拟试验结果每小时输出一次。
3 试验方案设计考虑模式中对流过程与强降水预报关系密切,首先选取对降水有显著影响的积云对流参数化方案(Kain-Fritsch Eta),分别从其内含的对流激发函数和质量通量的不确定性出发,设计了第一组试验(试验1),即对KFE中对降水预报影响较明显的一些经验性参数在合理取值范围内给予随机性调整以构造集合预报成员,试验研究模式的此类不确定性对“75.8"大暴雨预报的影响。这些参数包含在对流激发函数和质量通量的计算中,包括:由垂直速度引起的温度扰动、由相对湿度引起的温度扰动、云半径、对流有效位能释放的时间、夹卷率和湍流动能。表 1列出了这些参数的简要说明,并给出了参数可能取值的范围,集合成员其组成形式如表 2所示。
|
|
表 1 Kain-Fritsch Eta积云对流参数化中所选择的试验参数 |
|
|
表 2 试验1中各集合成员的参数取值 |
模式的不确性对降水预报的影响还体现在模式的分辨率和对流参数化方案,为此设计了第二组试验(试验2),即利用模式不同分辨率和不同物理参数化方案的组合来进行中尺度集合试验,构造8个集合成员。成员组合方式如表 3所示,表中星号注明为高分辨率成员(成员1、成员3、成员5),模式分辨率为10km,模式时间步长180秒;低分辨率的成员,模式分辨率30km,模式配置情况同试验1中控制预报。
|
|
表 3 基于不同模式分辨率和参数化方案构造的试验2集合成员 |
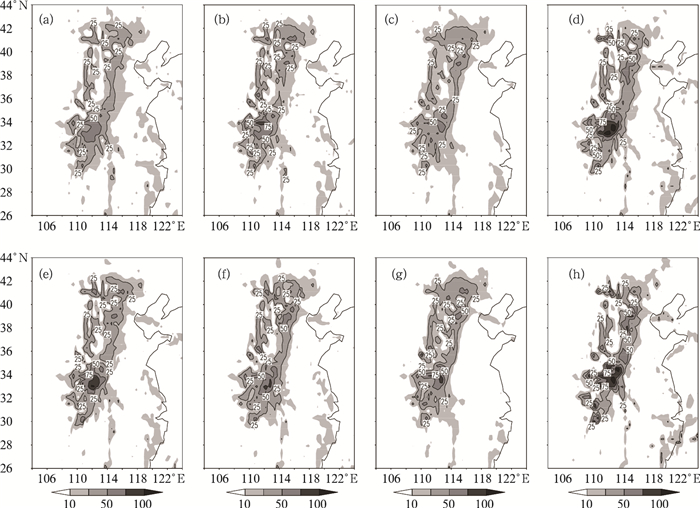
邮票图给出了全部集合成员预报的整体情况,它可以从不同角度了解未来大气发展的可能性。图 2给出了试验1中8个集合成员预报的8月6日至7日24小时累计降水量。整体上看,各个成员所预报出的降水落区都相差不大,雨带都呈东北—西南向分布,从河北延伸到湖北,降水中心都集中在河南省的中部和西南部地区。在控制试验的降水预报中,可以看到:暴雨区的最大日降水量为70mm,与实况(图 1)相比,降水强度明显偏小。在其余的集合成员模拟预报中,发现:通过对积云对流参数化中不同参数的组合和调整,降水的落区相差不大,基本都是反映出了台风入侵后的状况,但是降水的强度却有明显的差别:有的成员能预报出100mm以上的降水,而有的成员降水较之控制预报却明显偏小。从整体上看,有3个成员的预报最大日降水量在100mm以上,即成员4为120mm,成员5为100mm,成员8为110mm;降水最少的是成员3,仅有60mm。这种差异表明,模拟预报的“75.8"大暴雨对积云对流参数化方案(Kain-Fritsch Eta)中所含参数的取值是较敏感的。
|
图 2 试验1各成员预报的8月6日至7日累计24小时降水量 a—h表示成员1至成员8,其中成员1为控制试验, 单位:mm |
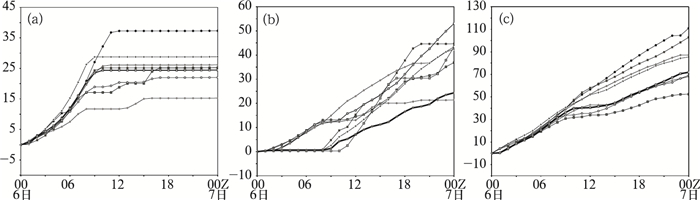
为了考察模拟暴雨过程的时间演变, 选取驻马店、许昌和南阳3站,给出其预报累计降水量的时间变化图(图 3)。由图 3可见,三个站点的情况各不相同:各成员模拟预报的驻马店站降水开始时间一致,即从积分一开始就能持续降水9小时, 3小时后各成员模拟降水量的差异才逐步显现出来,这也体现出参数取值差异对降水的影响需要通过一定时间的积累才能显现。从图 3a中看到驻马店站的模拟降水主要发生前12小时,在此后12小时各成员模拟的6日降水过程基本结束,只有少数成员产生少量降水。控制预报的24小时累积降水量为25mm,而各成员之间的差异较大, 最小日降水量仅为15mm,与控制预报相比,减小了约40%;而模拟预报最大日降水量约38mm,比控制预报的降水量增加了约50%。成员间的模拟日降水量差异幅度约25mm,达到了中雨的量级。许昌的情况与驻马店不同,基本可以把成员看成两类,一类在积分初期就能产生降水,而另一类在9小时后才陆续产生降水,后续降水情况成员间表现各异,较为复杂,整体来看,后续12小时为主要的降水时段,控制预报产生了约23mm降水,而集合成员中模拟预报日降水量最大值为53mm,与控制预报相比,降水量增加了一倍。成员间的模拟日降水量差异幅度约30mm,胜过了控制预报所预报的降水量。南阳的情况与驻马店、许昌不同,各成员的模拟降水均持续了24小时,差异主要在积分9小时后显示出来,有半数成员的模拟降水强度开始缓慢减弱,而另外4个成员的模拟降水强度则稳定少变,但整体看来,在南阳的模拟降水强度最大,且与实况最为吻合,其中, 控制试验的预报日降水量达到60mm以上的暴雨,各成员中模拟日降水量最小也有约40mm,比控制预报偏少33%,个别成员的模拟日降水量达到110mm以上的大暴雨,成员之间的模拟日降水量差异幅度达到了60mm。无论是图 2给出的成员间整体的降水地理分布,还是图 3从单站的降水时间变化,可以看到:调整积云对流参数化中的参数值,会影响到积云对流的激发,使得降水发生的时间有所不同,进而影响后续降水的发展,最终对降水预报产生不同的结果, 较控制预报而言,集合成员的模拟降水过程的差异显著。可见,对于影响对流降水发生、发展的对流参数化方案内在的敏感性参数,很值得更多深入的试验研究,这既是影响对流降水预报的关键,其间存在的不确定性也关系到这类对流降水的可预报性问题。
|
图 3 驻马店(a, 32.54°N、114.01°E)、许昌(b, 34.01°N、113.81°E)和南阳(c, 33.01°N、112.31°E)24小时降水量的时间序列图 粗黑线为控制预报,单位:mm |
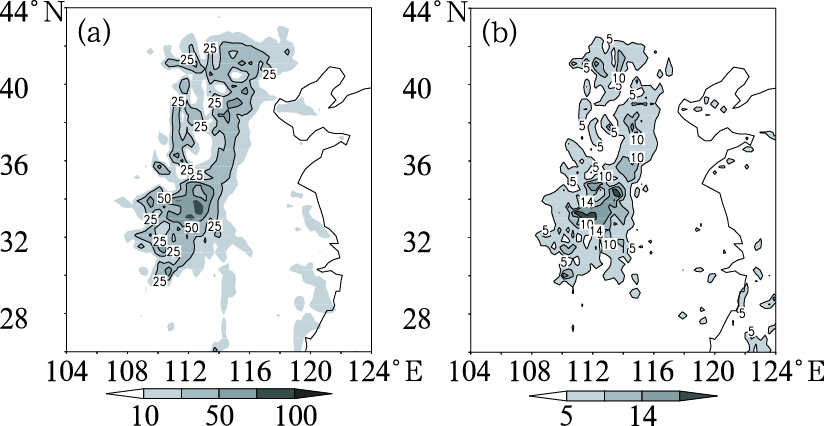
图 4给出的是试验1的8个成员预报24小时累计降水量的集合平均(图 4a)和离散度图(图 4b)。与图 2中的控制预报相比较, 从雨带的分布看,控制预报和与集合平均的差异不大,雨带呈东北西南向分布,在河南省的中部和西部地区出现了强的降水中心,在集合平均图上,大于50mm强雨区的范围稍有所扩大;从降水强度看,控制预报的日降水量只有70mm,而集合平均达到了90mm,接近大暴雨的强度,强降水中心更加突出,说明简单的集合平均预报,也能增加约30%的降水量,降水强度预报得到一定程度的改善;从图 4的离散度分布,可以看到它与雨区分布有很好的空间相关性,对于成员间模拟的雨区分布和范围的差异不大;而成员间模拟的强降水中心则各不相同,即存在较大的离散度。这种集合平均和离散度的空间分布,说明各个成员之间存在着合理的差异,离散度大的区域也从一个侧面反映了该地区的此类模式不确定性较大,在强降水预报中不可忽视。
|
图 4 试验1 24小时累计降水的集合平均(a)和集合离散度(b)(单位:mm) |
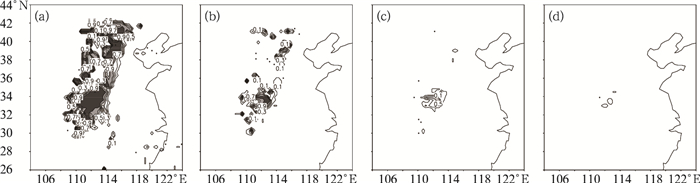
集合预报的一个重要产品是概率预报,假设每个成员的权重相同,对模式输出的每个格点值,计算其大于某一临界值的概率。显然从概率预报的角度来看,选择的成员越多对于这类产品的参考价值越高。在试验1中,计算了基于8个成员的24小时累计各级降水的概率。图 5分别给出大于25mm、大于50mm、大于75mm和大于100mm的降水概率。模式能够在一定程度上表现这次大暴雨过程,但是降水强度偏小,50mm以上的大雨区除华北个别地区外,主要发生在河南省,其降水概率达到了50%,更大强度的降水在相对较小的区域内发生,在河南的强降水中心处,大于75mm的概率也超过了50%,同时注意到:大于100mm也在该中心有所反映,虽然降水概率较小,但是对于这样极端的降水过程,小概率的事件不容忽视。
|
图 5 试验1的模拟24小时累计降水量大于(a)25mm(b)50mm(c)75mm(d)100mm的概率分布(阴影区为概率大于50%) |
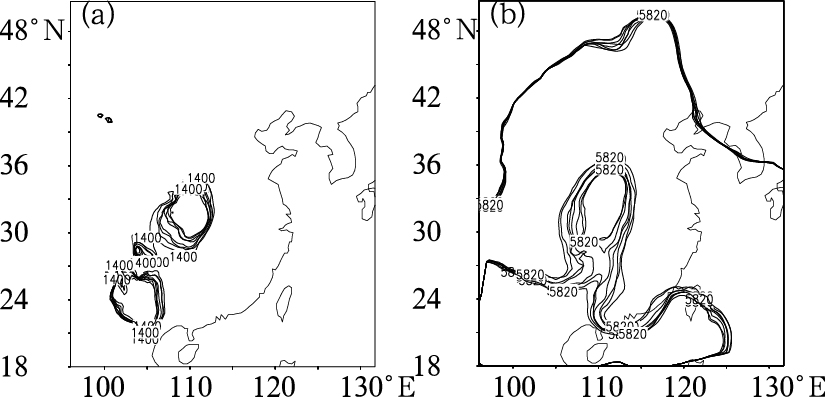
这次河南大暴雨过程是由多种天气系统造成的,其中最主要的是台风,同时西风带高空槽也处于停滞状态,向该地区输送了几次冷空气,选取850hPa和500hPa来看一下形势场的发展情况。图 6给出模拟预报的特征线(5820gpm)面条图,可以看到:河南、湖北一带主要受到了台风变性低压的影响,在中低层的850hPa(图 6a), 图形呈现出一定的离散状态,但1400gpm等值线一个主要位于河南省西部地区和湖北大部,一个则在云南省境内,对于河南地区,控制预报的低压中心范围较各成员都偏小。在500hPa(图 6b), 对于高纬地区,成员间的预报差异很小,而对于中纬地区的情况,特别是对位于河南、湖北两省的低压系统,差异较大,有的成员预报能把低值系统分离,控制预报对系统的预报范围仍然偏小,特征线表现出明显的发散状态,说明这一地区模拟预报的不确定性较大。
|
图 6 1975年8月7日0000UTC试验1中各成员模拟的等位势线面条图 a.850hPa1400gpm等值线,b.500hPa5820gpm等值线(黑线为控制预报,单位:gpm) |
为了从模拟形势场分析这次降水过程,图 7给出8月6日1800UTC3个层次的位势高度场的离散度分布情况。500hPa上,在河南省的西南部有一个大值中心,结构很清晰,中心最大强度是3.5gpm;同样在700hPa,在略偏西的位置,也有一个大值中心,强度是4gpm;850hPa上,几乎在同样的位置,这个大值区的强度也是4gpm。可见,从大气中低层至中层,离散度大值区的水平结构是比较相似的,且与强降水落区的位置对应较好,在垂直结构上,也表现了一定的一致性。

|
图 7 1975年8月6日1800UTC各层次位势高度场的离散度 a.500hPa,b.700hPa,c.850hPa(单位:gpm) |
图 8给出的是在试验2中基于高分辨率模式的3个成员所计算得出的24小时累计降水量分布。在图 8a中,出现了两个强降水中心,分别是在河南省的西南部和湖北省的西部,日降水量分别是100mm和120mm;图 8b的雨带分布与图 8a相似,但25mm以上中雨的降水落区有所扩展,河南境内的强降水区更加集中,湖北省西部的强降水中心未出现,河南的强降水中心的日雨量达到110mm;图 8c由于采用Betts-Miller-Janjic对流参数化方案,降水分布与前两幅图稍有区别,雨带显得更连续,降水的区域也较广,50mm以上的大雨区分布较之前面两组试验的结果要广,从河北省一直延伸到了河南省,最大日降水量仅有70mm,未出现明显的大于100mm以上的暴雨中心。可见,这类强降水天气的预报,积云对流参数化方案的选择存在着较大的不确定性。
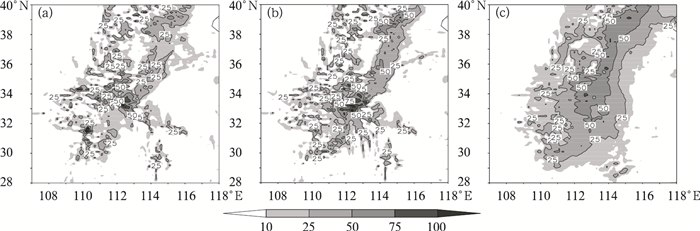
|
图 8 试验2中3组高分辨率模式24小时累计降水量(单位:mm) |
把模式采用高低分辨率运行结果综合到一起,图 9给出了综合以后的24小时累积降水量。比较图 8和图 9,可以看到:两组预报结果对于雨带的分布非常相似,但暴雨强中心的量值和落区上略有差别,且图 9中的暴雨中心的量值从左到右分别是140mm,130mm和90mm。较之模式仅采用高分辩率的预报结果相比,降水量约提高了20%~30%。可见,采用不同的模式分辨率和物理参数化方案的集合后,简单的集合平均结果能够在一定程度上给暴雨强度预报提供有用的信息,比单一模式分辨率的预报结果有更多的参考价值。同时也发现:主要雨区的分布和结构是由高分辨率的模式反映出来的,而雨强的差异和改变则主要反映出了低分辨率的模式之间存在的差异。此外,可以根据预报的需求,把混合后的这3个成员再做集合平均,得到更进一步的集合产品。
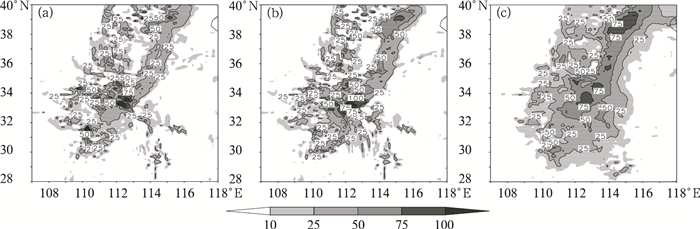
|
图 9 试验2中考虑“混合分辨率”集合后的24小时平均累计降水量(单位:mm) |
考虑对流过程与强降水预报的密切关系,对模式对流过程的不确定因素(参数化方案、经验性参数、网格分辨率等)对“75.8"大暴雨预报的影响进行模拟试验研究,即在相同初始场和同一模式框架基础上作对比试验,并探讨中尺度集合预报方法对提高“75.8"大暴雨预报能力的可能性。应用中国气象局新一代数值预报模式(GRAPES-Meso)和近年发展的中尺度集合预报技术对改善河南“75.8"大暴雨过程的可能性问题展开研究,试验1针对与强降水有显著影响的积云对流参数化方案(Kain-Fritsch Eta)中的参数在合理范围内进行调整来构造集合成员,试验2用模式的不同分辨率(30km、10km)和不同物理参数化方案的多种组合进行中尺度集合预报试验。通过对一些集合产品和对形势场、降水场的分析,得到以下结果:
(1) 积云对流参数化方案中不同参数取值对降水的影响各不相同。对降水落区的影响不很显著,但对降水强度的影响不可忽略,即降水强度对参数的不确定性具有敏感度,因而集合平均在一定程度上对降水强度的改善较明显,平均后的暴雨区最大降水量预报为90mm/24h,比“确定性"预报(控制试验)值70mm/24h改善了约30%,最佳的单个成员模拟暴雨区最大降水量(120mm/24h)比控制试验预报提高了70%。从时间演变上看,不同的参数取值会影响到积云对流的激发时间,使降水发生的时间有所不同,进而影响后续降水的发展,最终对降水预报产生不同的结果。
(2) 由试验1的模拟结果分析可见,对于影响强对流发生、发展的各种对流参数化方案中的敏感参数有待更深入的研究,这不仅对改进高分辨率数值模式的确定性预报,而且对于发挥中尺度集合预报技术在暴雨预报中的有效性能,都是十分必要的。
(3) 从试验2的集合试验结果可以看到:简单的集合平均能在一定程度上改善降水强度的预报,与高分辩率模式预报结果比较,暴雨中心降水量约提高了20%~30%。对于雨区的分布和结构主要取决于模式的高分辨率,而雨强的差异则主要反映出了低分辨率模式成员(不同对流参数化方案组合)之间存在的差异。
(4) 为了探讨中尺度集合预报的可行性,探讨中尺度集合预报是否比单一“确定性预报"(即控制预报)带来某些好处。两组试验集合平均都在一定程度上改善了“75.8"大暴雨过程的确定性数值预报的结果,这表明中尺度集合预报方法可在一定程度上减小模式不确定性对降水预报结果的影响,简单的集合平均也能增大强暴雨中心预报的可信度,体现其对模式不确定性的量化作用。
(5) 两组集合试验成员都是从模式对流过程的参数化或是模式水平分辨率入手,所有成员的模拟试验均采用同一的变量初始场,并未考虑初始场的不确定性对模拟试验的影响,这部分内容有待在下一步工作中展开。
(6) 两组试验虽然集合预报较之控制预报,预报效果有改善,但与实况降水相比,预报能力仍显不足,究其原因,可能是多方面的:初始资料所包含信息的多样性和准确性,数值模式对地形表现的客观性,对物理过程描述的真实性等,都会影响到对这类极端强降水天气的预报。
(7) 此外,文章主要针对个例展开试验,对于试验方案的代表性和实用性的问题,还需要更多的个例试验来加以证明,不单是针对强降水过程的个例,还需要对一些系统性降水,或是没有降水的个例做更多的试验。
致谢:在论文的完成过程中,得到了朱永禔研究员的指导,在此表示感谢!
| [1] |
陶诗言, 等. 中国之暴雨[M]. 北京: 科学出版社, 1980: 147-162.
|
| [2] |
南方周末. 2005年8月25日第1124期.
|
| [3] |
丁一汇, 蔡则怡, 李吉顺. 1975年8月上旬河南特大暴雨的研究[J]. 大气科学, 1978, 2(4): 276-289. |
| [4] |
758暴雨会战北京组. 758河南特大暴雨的动力分析[J]. 气象学报, 1979, 37(4): 45-55. DOI:10.11676/qxxb1979.038 |
| [5] |
赵思雄, 周晓平. 风场在预报暴雨发生中的作用——1975年8月上旬特大暴雨的数值试验[J]. 大气科学, 1984, 8(1): 1-6. |
| [6] |
蔡则怡, 宇如聪. LASG-η坐标有限区域数值预报模式对一次登陆台风特大暴雨的数值试验[J]. 大气科学, 1997, 21(04): 460-471. |
| [7] | |
| [8] |
Kain Jone S. The Kain-Fritsch Convective Paramaterization: An Update, 2004[J]. Journal of Applied Meteorology, 2004, 43: 170-181. DOI:10.1175/1520-0450(2004)043<0170:TKCPAU>2.0.CO;2 |
| [9] |
Brooks. H.E., M. S. Tracton, D. J. Stensrud, et al. Short-range ensemble forecasting: Report from a workshop, 25-27 July 1994[J]. Bull. Amer. Me teor. Soc., 1995, 76: 1617-1624. DOI:10.1175/1520-0477-76.9.1617 |
| [10] |
Harrison M.S. Analysis and model dependcies in medium-range forecast: two transplant case studies[J]. Quart. J. Roy. Meteor. Soc, 1999, 126: 711-724. |
| [11] |
Hou D, Kalnay E, Droegemier K.K. Objective verification of the SA MEX'98 ensemble forecasts[J]. Mon. Wea. Rev., 2001, 129: 73-91. DOI:10.1175/1520-0493(2001)129<0073:OVOTSE>2.0.CO;2 |
| [12] |
Alberto Arribas. Results of an initial stochastic physics scheme for the Met Office Unified Model[R]. Exeter: Forecasting Research Technical Report No. 452, 2004.
|
| [13] |
张大林. 各种非绝热物理过程在中尺度模式中的作用[J]. 大气科学, 1998, 22(4): 548-561. |
| [14] |
陈静. 物理过程参数化方案对中尺度暴雨数值模拟影响的研究[J]. 气象学报, 2003, 61(2): 203-218. DOI:10.11676/qxxb2003.019 |
| [15] |
顾建峰. 不同深对流参数化方案在降水预报中的比较试验[J]. 气象, 1999, 25(4): 39-44. DOI:10.7519/j.issn.1000-0526.1999.04.008 |
| [16] |
段旭, 王曼, 刘建宇, 等. 低纬高原地区MM5v3不同参数化方案降水模拟试验[J]. 气象, 2006, 32(4): 16-23. DOI:10.7519/j.issn.1000-0526.2006.04.003 |
| [17] |
伍红雨, 陈德辉, 徐国强. 不同物理过程参数化方案对贵州降水预报的敏感性试验[J]. 气象, 2007, 33(4): 23-28. DOI:10.7519/j.issn.1000-0526.2007.04.004 |
| [18] |
Houtekamer P.L, Lefaivre L, Derome J, et al. A System simulation approach to ensemble prediction[J]. Mon. Wea. Rev., 1996, 124: 1225-1242. DOI:10.1175/1520-0493(1996)124<1225:ASSATE>2.0.CO;2 |
| [19] |
Personal Communication with Dr Martin Charron.
|
| [20] |
Epstein E S. Stochastic dynamic prediction[J]. Tellus, 1969, 21: 739-759. |
| [21] |
Houtekamer P.L, Derome J.. Methods for ensemble prediction[J]. Mon. Wea. Rev, 1995, 123: 2181-2196. DOI:10.1175/1520-0493(1995)123<2181:MFEP>2.0.CO;2 |
| [22] |
Du J, Mullen S. L, Sanders F. Short-Range Ensemble Forecasting of Quantitative Precipitation[J]. Mon. Wea. Rev., 1997, 125: 2427-2459. DOI:10.1175/1520-0493(1997)125<2427:SREFOQ>2.0.CO;2 |
| [23] |
Mullen S.L, R Buizza. The Impact of Horizontal Resolution and Ensemble Size on Probabilistic Forecasts of Precipitation by the ECMWF Ensemble Prediction System[J]. Weather and Forecasting, 2002, 17: 173-191. DOI:10.1175/1520-0434(2002)017<0173:TIOHRA>2.0.CO;2 |
| [24] |
Roebber P J, D M Schultz, B A Colle, et al. FORECAST'S FORUM Towards im proved prediction: High-resolution and ensemble modeling system in operations[J]. Weather and Forecasting, 2004, 19: 936-949. DOI:10.1175/1520-0434(2004)019<0936:TIPHAE>2.0.CO;2 |
| [25] |
Mass C F, David Ovens, Ken Westrick, et al. Does increasing horizontal resolution produce more skillful forecasts[J]. Bull. Amer. Meteor. Soc, 2002, 93: 407-430. |
| [26] |
Du J. Hybrid Ensemble Prediction System: A New Ensemble Approach, 2004. [C]Symposium on the 50th Anniversary of Operational Numerical Weather Predicti on.
|
| [27] |
陈静. 中尺度暴雨短期集合预报研究[M]. 北京: 中国气象科学研究院, 2003.
|
| [28] |
谭燕, 陈德辉. 基于非静力模式物理扰动的中尺度集合预报试验[J]. 应用气象学报, 2007, 18(3): 396-406. |
| [29] |
王晨稀. 短期集合降水概率预报试验[J]. 应用气象学报, 2005, 16(1): 78-88. DOI:10.11898/1001-7313.20050110 |
| [30] |
牛震宇, 张立凤. 基于集合预报思想对一次暴雨过程的数值模拟[J]. 解放军理工大学学报(自然科学版), 2006, 7(1): 73-79. |
 2008, Vol. 34
2008, Vol. 34