2. 南京信息工程大学气象工程管理研究中心;
3. 南京信息工程大学经济管理学院;
4. 江苏省气象科学研究所
2. Research Center for Meteorology Engineering & Management;
3. Department of Economic Management NUIST;
4. Jiangsu Provincial Meteorological Institute
全球气候变化(气候变暖)已经成为全球高度关注的重大问题,气候变化的影响在各个领域广泛展开。我国的气候变化影响研究主要集中在农业、水资源、自然生态系统和海岸带,对其他领域的研究尚未成气候[1]。其中气象学和经济学交叉领域的研究越来越受到国内外专家学者的重视,相关研究已经越来越专业和深入。Dutton(2002)[2]研究了气象因子对美国各行业产值的影响,揭示了气象因子与美国经济之间的关系。美国也已经开展了规模较大的“美国不同经济行业对天气敏感性评估项目[3]”(OUSSSA,2006),引进了计量经济学的思想和方法,通过构造加入气象因子(气温、降水)的类似生产函数的经济模型来揭示行业的天气敏感性。郑艳等[4](2006)应用计量经济学中的协整分析方法研究了城市增温的主要社会经济影响因子。罗慧等[5-6](2007,2008)合理运用相关数学方法,定量分析了奥运气象服务的社会经济效益。扈海波等[7](2008)以AHP模型为基准对气象服务产品的社会经济效益进行定量化评估。可见,一方面气象学和经济学的交叉研究呈现出广阔的发展前景,另一方面也说明注重融合经济学的主流理论是今后研究的发展方向。
目前,如何科学定量地评估气象因子对各行各业的影响是一项十分重要的工作,也是当前相对薄弱的工作。国外如美国[2-3]已经有了系统的研究方法,并在不断深入[8]。国内的研究尚不多见,张钛仁等[9](2007)应用专家评估法对高气象敏感行业进行了评定和排序。本文尝试运用计量经济学中完善的协整理论初步研究气温因子对行业的影响。考虑到气候与行业分布的局地性,借鉴美国的研究以州为单位,我们选择南京的主要行业为研究对象,即研究气温变化对南京主要行业的影响,揭示南京市主要行业的气温敏感性。
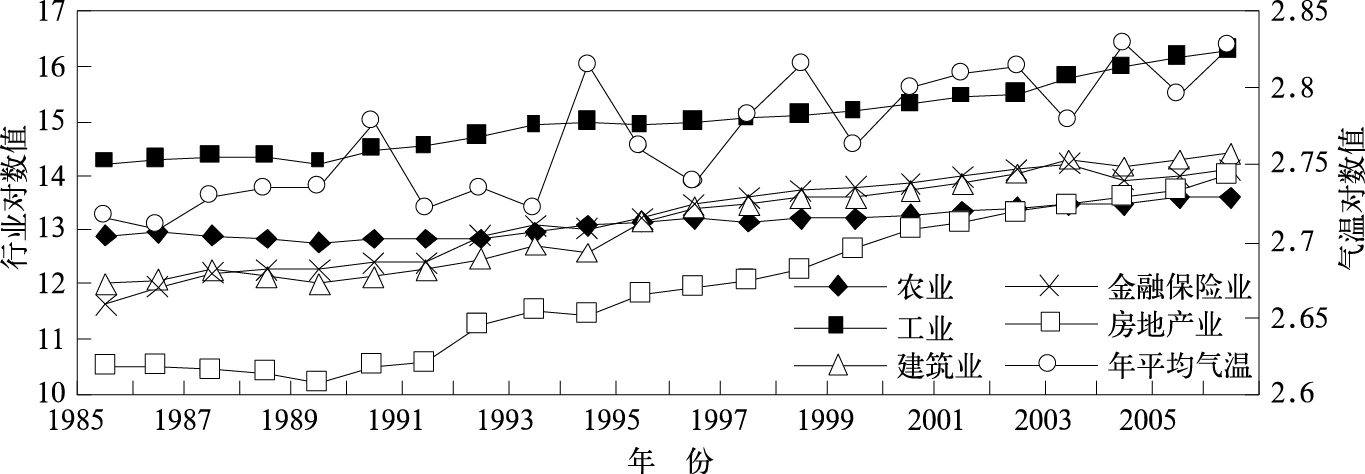
1 数据收集和处理本文拟通过分析气温跟行业产值之间的耦合关系来揭示气温变化对行业的影响。通过查阅历年的《南京统计年鉴》,基于数据可得性(主要受统计口径变化影响),得到了1985—2006年5个主要行业产值22年的当年价格序列,包括农业、工业、建筑业、金融保险业和房地产业,涵盖了第一、二、三产业。然后按照《中国统计年鉴2007》中的价格定基指数,求得以2006年价格为基准的南京主要行业1985—2006产值的可比价格序列。鉴于产值序列是年际数据,因此采用南京站1985—2006年的年平均气温序列。然后为消除数据的异方差,对这些数据都做了取对数处理, 记为农业(AG)、工业(I)、建筑业(A)、金融保险业(F)和房地产业(RE)(以下分析都是针对各变量的对数序列,不再特别说明)。最后对这些序列做平稳性检验,发现其水平值(原始值)都通不过检验(结果见表 1),因此这些序列都是非平稳的。自然我们想到了非平稳序列建模的常用经济计量方法——1987年Eangle和Granger[10]提出的协整理论及其方法。并且气温对数序列及南京主要行业的产值对数序列如图 1所示,所有序列均呈上升趋势,说明气温跟行业产值之间可能存在协整关系。
|
|
表 1 各对数序列的平稳性检验结果 |
|
图 1 南京市主要行业年产值及年平均气温对数序列图 |
协整理论主要思想是:虽然一些变量本身是非平稳序列,但如果它们的线性组合是平稳的,则这种平稳的线性组合就被称为协整方程,且可被解释为变量之间的长期稳定的均衡关系。协整方程的建立一般分为四步[11]:平稳性检验、协整性检验、误差修正模型、因果检验。
2.1 序列平稳性检验如果一个时间序列具有稳定的均值和方差,则这个序列是平稳的,否则就是非平稳的。如果一个序列必须经过d次差分后才能平稳,则此序列为d阶单整序列,记为I(d)。对于两个序列而言,具有相同的单整阶数,是序列之间具有协整性的必要条件。
一般采用ADF检验方法对序列平稳性进行检验。即对时间序列xi建立最小二乘回归(OLS)方程:
| $\Delta {\mathit{x}_\mathit{t}} = \left( {\mathit{\rho - }{\rm{1}}} \right){x_\mathit{t}}_{ - 1} + \sum\limits_{j = 1}^p {{\mathit{\lambda }_\mathit{j}}\Delta } {\mathit{x}_{\mathit{t - j}}} + \varepsilon _\mathit{t} $ | (1) |
其中:ε为误差项(下同)。并对方程中的系数ρ=1进行检验,在这种检验方法中原假设是:ρ=1,即序列是不平稳的;对立假设则是:ρ<1,即序列是平稳的。
2.2 序列间协整性检验变量序列之间的协整性衡量了两个变量变化趋势之间的长期稳定关系。按照文献[10]提出的两变量协整检验的两步检验法,如果已经判断两个序列xt和yt是非平稳的,但其都是d阶单整序列。则:
第一步建立协整回归方程:
| ${x_\mathit{t}} = \mathit{\alpha + \beta }{\mathit{y}_\mathit{t}} + {\mathit{\varepsilon }_\mathit{t}} $ | (2) |
并通过OLS回归得到
| ${\hat x_\mathit{t}} = \mathit{\alpha + \beta }{\mathit{\hat y}_\mathit{t}} + {\mathit{\hat \varepsilon }_\mathit{t}} $ | (3) |
第二步,通过对残差
根据Granger定理,如果时间序列xt和yt之间具有协整关系,还可以有另外一种等阶形式,即误差修正模型(以下简称ECM),其建立方法是:
1.求模型yt=k1x1+εt的OLS估计,得到
| ${\hat \varepsilon _\mathit{t}} = {\mathit{y}_\mathit{t}} - {\mathit{\hat k}_{\rm{1}}}{\mathit{x}_{\rm{1}}} $ | (4) |
2.用
| $\Delta {\mathit{y}_\mathit{t}} = {\mathit{\beta }_{\rm{0}}} + \left( {{\mathit{\beta }_{\rm{1}}} - 1} \right){\varepsilon _{\mathit{t} - 1}} + {\mathit{\hat \beta }_{\rm{2}}}\Delta {\mathit{x}_\mathit{t}} + {\varepsilon _\mathit{t}} $ | (5) |
再用OLS方法估计其参数。
2.4 序列间因果关系检验目前变量之间因果关系衡量应用最为广泛的是Granger因果关系检验方法。Granger因果关系检验的基本思路是:如果变量X的历史信息有助于变量Y预测精度的改善,则认为X对Y存在Granger因果关系。Granger因果关系检验的具体方法是:建立两变量自回归模型:
| ${y_t} = {\mathit{\alpha }_{\rm{0}}}{\rm{ + }}\sum\limits_{i = 1}^m {{\mathit{\alpha }_\mathit{i}}{\mathit{y}_{\mathit{t - i}}} + \sum\limits_{i = 1}^m {{\mathit{\beta }_\mathit{i}}{x_{t - i}} + {\varepsilon _{1t}}} } $ | (6) |
| ${x_t} = {\mathit{\alpha }_{\rm{0}}}{\rm{ + }}\sum\limits_{j = 1}^m {{\mathit{\alpha }_\mathit{j}}{\mathit{y}_{\mathit{t - j}}} + \sum\limits_{j = 1}^m {{\mathit{\beta }_\mathit{j}}{x_{t - j}} + {\varepsilon _{2t}}} } $ | (7) |
对模型中的参数进行估计,并对βi(i=1, 2…,m)进行检验,这个假设实际上等同于“X不是引起Y变化的原因”。如果拒绝了该假设,我们就可以得出X对Y存在Granger因果关系的结论。同样对βj(j=1, 2…,m)进行检验,从而判断Y对X是否存在Granger因果关系。
下面,我们就采用协整理论分析气温对南京主要行业的影响。
3 气温对南京市主要行业影响研究根据上述协整理论和方法,采用Eviews5.0计量分析软件[11]进行相关运算:
3.1 序列平稳性检验采用上述ADF检验方法,根据AIC准则确定最佳滞后阶数,这里都取为3,计算结果如表 1。
从结果可以看到,大部分序列都在5%显著水平以上通过ADF序列平稳性检验,仅有AG序列是在10%的显著水平上勉强通过检验。我们可以认为这些序列都是1阶单整序列,满足协整分析前提。
3.2 协整性检验建立如式(2)所示回归方程,采用OLS法估计其参数,结果如表 2。
|
|
表 2 气温与各行业产值间的协整方程估计结果 |
根据协整回归方程结果,通过式(3)变换得到残差计算公式:
|
|
表 3 各协整方程残差序列的平稳性检验结果残差 |
从结果看,各残差序列都通过显著性5%以上的序列平稳性检验,证明气温和各主要行业产值之间存在长期稳定的关系。具体来讲,根据协整回归方程估计结果,气温T的系数的倒数可以看做是气温对行业产值的长期弹性:气温每升高1%,农业产值增长0.199%、工业增长0.083%、建筑业增长0.063%、金融保险业增长0.065%、房地产业增长0.041%。可见气温升高对南京市各主要行业均具有正向促进作用,其作用大小或者说行业对气温升高的长期气温敏感度大小排序为:农业>工业>金融保险业>建筑业>房地产业。
定量分析结果与文献[8]的结果吻合,与实际经验也相符。敏感度最高是农业,农业包括农林牧副渔,有研究[12-13]表明气温升高对南京地区的农作物生产有负面影响:气温每升高1℃,水稻减产6%左右,小麦减产3.44%左右。但实际情况却是2006年年平均气温比1999年高了1℃还多,农作物产值非但没有减少,反而比1999年增产了47%(按不变价格计算),即便承认农业生产率提高因素,但是考虑到这个增产是建立在耕地比1999年减少20%以上的,可见气温升高对农业整体的促进作用是不能忽视的;敏感度最低是房地产业可以理解,因为无论气温怎么变化,人类的住房需求都几乎不受其影响;工业包括水电供应部门、能源矿产部门等,这些部门对气温具有较高的敏感度也是具有说服力的;建筑业与房地产业关系密切,因此建筑业对气温敏感度相对较低是不言而喻的;气温升高引起极端天气增多,灾害事故发生率也增加,因此金融保险业对气温比较敏感且高于建筑业是合理的。
3.3 误差修正模型(ECM)ECM可以反映变量间的短期波动和长期均衡关系。对各对协整变量根据式(5)用OLS法估计得到ECM结果如表 4。
|
|
表 4 各协整变量的误差修正模型结果 |
在上面的ECM中,各差分项反映了短期波动的影响。农业(AG)的短期波动可分为两部分:一部分是AG自身以及气温(T)短期波动的影响,AG短期增长1%,T短期升高5.02%,反过来T升高1%,AG增长0.199%,我们把ΔT系数的倒数(1/β2)看作是气温对行业产值的短期弹性。同理,T短期每升高1%,I减少3.165%、A减少0.612%、F增长6.173%、RE减少1.524%;从表中得出的气温升高对南京市各主要行业的短期影响正、负作用都有,总的来看,气温升高对南京市主要行业的绝对短期影响排序,或者说是行业的短期气温敏感度排序是:金融保险业>工业>房地产业>建筑业>农业。这里所谓的短期影响是相对上述长期影响来说的,长期反映整体的趋势,短期则表示近几年的波动。一般来讲,从行业整体的角度探讨行业气象因子敏感性多注重于长期的整体趋势研究,毕竟影响行业的因素很多,气象因子通常并非主因,其短期的影响难以衡量。这里我们根据ECM的估计结果,可以初步揭示出行业短期气温敏感性的一些特点,与经验也比较相符。比如气温短期升高对工业的确存在负面影响,表现在高温桑拿天数的增多引起能源(如电力)供应的短缺,对企业造成的损失逐年递增;而南京地区农业基础条件好,气温短期升高带来的负面效应(如干旱、极端天气等)对其的影响就少,自然其正面效应(日照增多、CO2肥效作用)就得到加强。
另一部分是偏离长期均衡的影响。ECM项系数大小反映了气温对行业产值偏离长期均衡的调整力度,如当AG的短期波动偏离长期均衡时,气温以(-0.042)的反向调整力度将非均衡状态拉回到均衡状态。我们可以看到各个系数值都比较小,气温对工业和金融保险业的长期调整力度相对较大。总得来看气温对各行业的长期均衡修正能力几乎可以忽略不计。究其原因,与各行业的发展是多方面因素造成的有关,气温因子所起的作用是极微小的。
3.4 Granger因果关系检验协整分析的结果显示气温与南京市各主要行业产值之间存在协整关系,为进一步证实两者的关系,还要做Granger因果检验。根据AIC准则和SC准则确定待检验变量的最佳滞后阶数,结果如表 5。
|
|
表 5 各协整变量间的Granger因果关系检验结果 |
从表 5中结果看,对工业、建筑业、房地产业来说,气温跟它们都存在双向的Granger原因关系,进一步证实了气温对这些行业有正向促进作用,并且这些行业的发展对气温升高亦有显著的贡献。工业的贡献主要来自大量的碳排放,建筑业和房地产业的贡献则来自城市化进程带来的城市热岛效应加强。气温不是农业的Granger原因,同时农业是气温的Granger原因。这个结果有点意外,考虑到南京市的农业耕地从1985年的21.88×104hm2减少到2006年的16.37×104hm2,我们认为其可能原因是南京的城市化进程使得农业用地大量减少,一方面导致城市热岛效应增强,促使气温升高,使得农业成为气温的Granger原因;另一方面农业用地大量减少,但是农业产值反而持续增长,可见促使南京农业产值增长的主要原因在于农业劳动生产率的提高,因此气温就不是农业的Granger原因。但是气温对农业的长期正向促进作用是存在的,不过是作用相对小而已。对于金融保险业来说,因为南京的金融保险业虽然整体看是一个增长的态势,但在2004年有一个显著的拐点,产值比2003年减少了近30%,所以结果就是气温不是它的Granger原因。但是金融保险业的发展伴随着各行各业的发展,其他行业对气温升高的贡献就转嫁到它上面,这就导致它成为气温的Granger原因了。
4 小结本文通过严格的协整理论定量分析了气温对南京市主要行业的影响,说明协整理论不失为一种较好的评估气象因子对行业影响的方法,主要结论有:
(1) 根据协整检验的结果,证明气温与行业产值之间存在长期稳定的协整关系。
(2) 根据协整回归方程和误差修正模型定量分析的结果,得到了气温升高对南京市主要行业的长期以及短期影响,并给出了相应的气温敏感度排序,同时也得出气温对行业产值的长期均衡修正能力较小的结论。
(3) 根据Granger因果检验的结果,大多数行业与气温之间存在双向Granger因果关系,进一步证实了气温变化的确对南京市主要行业存在影响。为了更准确地评估各行业的气象因子敏感性,今后的工作在于进行多因子(包括其它影响因子或气象因子)的协整分析,同时把研究对象扩展到更多的行业和地区。
| [1] |
《气候变化国家评估报告》编写委员会. 气候变化国家评估报告[M]. 北京: 科学出版社, 2007.
|
| [2] |
Dutton J.R. Opportunities and priorities in a new era for weather and climate services[J]. Bull. Am. Meteorol. Soc, 2002, 93: 1303-1311. |
| [3] |
Peter H. Larsen. An evaluation of the sensitivity of U. S. economic sectors to weather[OL]. http://papers.ssrn.com/sol3/papers.cfm?abstract_id=900901,2006.
|
| [4] |
郑艳, 潘家华, 吴向阳. 影响北京城市增温的主要社会经济因子分析[J]. 气候变化研究进展, 2006, 2(4): 188-192. |
| [5] |
罗慧, 谢璞, 俞小鼎. 奥运气象服务社会经济效益评估个例分析[J]. 气象, 2007, 33(3): 90-94. |
| [6] |
罗慧, 谢璞, 薛允传, 等. 奥运气象服务社会经济效益评估的AHP/BCG组合分析[J]. 气象, 2008, 34(1): 59-65. |
| [7] |
扈海波, 王迎春, 李青青. 采用AHP方法的气象服务社会经济效益定量评估分析[J]. 气象, 2008, 34(3): 86-92. DOI:10.7519/j.issn.1000-0526.2008.03.013 |
| [8] |
贾朋群, 戴洋, 苗森. 气象服务经济效益评估综合评述[J]. 中国气象学会2007年年会——气象软科学论坛, 2007. |
| [9] |
张钛仁, 宋善允, 田翠英, 等. 中国行业气象服务效益评估方法与分析研究[J]. 气象软科学, 2007, 4: 5-14. |
| [10] |
Engle, Robert F, FGranger C. W. J. Co-integration and Error Correction: Representation, Estimation and Testing[J]. Econometrica, 1987, 55: 251-276. DOI:10.2307/1913236 |
| [11] |
高铁梅. 计量经济分析方法与建模——Eviews应用及实例[M]. 清华大学出版社, 2006.
|
| [12] |
郑有飞, 万长建, 缪启龙, 等. 气候变化对水稻光合产量影响探索[J]. 南京气象学院学报, 1999, 22: 536-540. |
| [13] |
郑有飞, 万长建, 缪启龙, 等. 气候变化对小麦生产影响的数值模型研究[J]. 南京气象学院学报, 1999, 22(4): 645-651. |
 2008, Vol. 34
2008, Vol. 34