2. 国家气象中心
2. National Meteorological Center, CMA
气象要素的空间分布图,一般也称为色斑图[1],要求精确性(如:避免丢值)、视觉美观性(如避免常规算法所带来的大量的碎部产生等问题),插值算法的选择直接影响到色斑图的表现质量。目前各类插值算法较多,如:克里格(Kriging)插值法、加权反距离法(IDW)、Delaunay三角剖分线性内插、样条函数插值和Cressman客观分析等。
然而,一般的插值算法通常很难同时满足精确性和美观性要求,笔者在对常用的插值算法进行充分分析的基础上,借鉴人工天气图分析思路,采用逐级插值的分析方法,对逐步订正方法(Cressman算法)进行了改进与优化,并提出了一种新的称之为MCressman的插值方法,从而解决了一些现有插值算法中的关键技术问题。
1 算法分析 1.1 常用插值算法分析数据的空间插值方法很多,有多种分类方法。黄杏元等[2]依据已知点和已知分区数据的不同,可将空间数据插值分为点的内插和区域的内插,邬伦等[3]则对应分为空间内插和外推。影响区域空间插值精度的主要因素就是空间插值方法。目前不同领域内较为常用的插值方法有克里格(Kriging)插值法、加权反距离法(IDW)、Delaunay三角剖分线性内插、样条函数插值和Cressman客观分析等,这些方法在IDL、MATLAB、Surfer、Arc/info和ArcMap等数据分析处理软件以及气象数据客观分析研究中经常被采用。文献[4-5]对克里格(Kriging)插值法、加权反距离法、Delaunay三角剖分线性内插、样条函数插值和Cressman客观分析5种不同的空间内插方法进行比较研究,选用了中国区域内基本台站10年(1988年12月至1998年11月)的月降水量作为5种插值算法的试验数据。不同方法的插值结果反插到原始台站后的对比分析结果如表 1所示[5]。结果表明,Cressman客观分析法与原始台站最为接近, 反距离加权和双谐样条方法次之,而克里格与三角化线性方法则与原始台站偏离最大。Cressman客观分析方法是一种将离散点内插到规则格点引起误差较小的一种逐步订正的内插方法,因此被广泛应用于气象领域各种诊断分析和数值预报方案的客观分析中,因而Cressman方法第一次使客观分析成为了一门独立的科学[6]。
|
|
表 1 插值方法比较 |
Cressman客观分析方法是由Cressman[7]等在1959年提出的,其基本原理是先给定第一猜测场,然后用实际观测场逐步修正第一猜测场,直到订正后的场逼近观测记录为止。
| $ \alpha ' = {\alpha _0} + \Delta {\alpha _{ij}} $ | (1) |
其中
| $ \Delta {a_{ij}} = \frac{{\sum\limits_{k = 1}^K {\left( {W_{ijk}^2\Delta {a_k}} \right)} }}{{\sum\limits_{k = 1}^K {{W_{ijk}}} }} $ | (2) |
式中,αk为任意一气象要素(如:降水、风、温度等);α0是变量α在格点(i,j)上的第一猜测;α′是变量αk在格点(i,j)上的订正值;Δαk是观测点k上的观测值与第一猜测值之差;Wijk是权重因子,分别由香蕉形、椭圆形和圆形权重函数决定,在0.0~1.0之间;K是影响半径R内的台站数。Cressman客观分析方法最重要的是权重函数Wijk的确定,它的一般形式为
| $ {{W}_{ijk}}=\left\{ \begin{array}{*{35}{l}} \frac{{{R}^{2}}-d_{ijk}^{2}}{{{R}^{2}}+d_{ijk}^{2}}\ ,\ \ \ \ \ \ \ \ \ 当{{d}_{ijk}}<R & {} \\ 0,\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 当{{d}_{ijk}}\ge R & {} \\ \end{array} \right. $ | (3) |
其一般取为1、2、4、7和10几个常数[5]。dijk是格点(i,j)到观测点k的距离。
2 基于关键值的Cressman方法在气象降水分布图制作过程中,通常按24小时降水量(mm)的大小将其分为:小雨(1~9.9)、中雨(10~24.9)、大雨(25~49.9)、暴雨(50~99.9)、大暴雨(100~250)、特大暴雨(>250)这六个级别。尽管Cressman在气象方面应用最为广泛,最为贴近实际情况,但在降水插值中存在的最明显的问题是:如果在实况观测站数据(即离散点数据)中只有一个站点而其降水量恰好处于降水分级值附近,那么常规Cressman算法则会在其逐步订正过程中将该重要的站点值因内插订正而丢失。显然,这一至关重要的降水量信息在决策服务产品的制作过程中是不能丢失的。
另外,当台站资料分布极为不均时,如在一大片区域内如果只有一个较小集中区域有降水时(本文称为孤点),采用Cressman插值后该点会出现圆形插值区域,且范围过大,这样从视觉上会显得有些单调,不够自然。而且插值的边界会确定不合理——即有时会过大或应该有的地方没填上,有不知名碎块,区域性表现不强。
针对以上问题,为了满足气象决策服务的需求,本文在保留了传统Cressman优势的基础上对其进行了优化,提出了基于关键值的Cressman插值算法(以下称为MCressman算法),该方法既解决了传统Cressman算法在插值中存在的问题,又满足了精确性和美观性的要求。
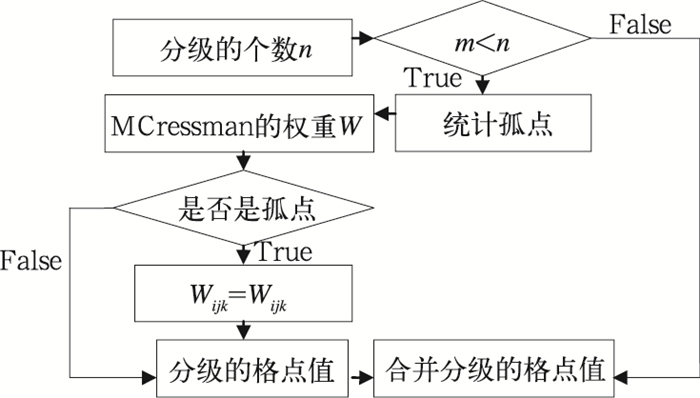
MCressman算法的基本思想如下:借鉴人工天气图分析思路,采用逐级插值的分析方法,在分析某一级时,只选择该级以上的观测点资料参与分析,以保证该级别不被平滑掉;并在Cressman算法中加入对不同的分级分配不同的权重,即在各自级别权重的基础上根据级别的不同加重或减轻权重随影响距离的增加而衰减的程度;以表现同一值在不同级别中的层次感,并对分析得到的格点值进行光滑是图形色块边界平滑、美观。同时为了保证插值边界的准确性,提出了离散点边界的提取、数据插补技术、格点光滑等技术。其主要原理如图 1所示。

|
图 1 改进算法的处理流程示意 |
MCressman需要解决的几个关键技术包括:边界搜索算法、数据插补、格点光滑。
3.1 边界搜索算法为有效保证插值的边界在一定的合理范围内,本文对离散点的边界作了如下处理:
(1) 对所有离散点进行缓冲区(buffer)分析,形成一系列圆形多边形区域,即找出每一离散点与其相邻的其他离散点,距离的选取可以参照数据的分布情况,如在全国范围内距离的取值为10km。
(2) 对每个离散点形成的缓冲区逐一求合并(union)操作,最终将形成若干个新的不规则多边形。对每一个参与合并过的多边形给出标记,记flag为1。
(3) 在(2)中如果多边形的flag为0即表示在一定范围内,它不与别的多边形区域相交,也表明了生成该圆形多边形的原离散点在一定的距离内周围没有其他离散点。因此,为了色斑图的美观,以该点为中心做一个较小的椭圆,以避免插值后形成规则的圆形区域。
(4) 对所有合并处理后的多边求其凸包,并对该凸包的边界进行光滑处理,在本文中采用了贝塞尔曲线算法进行处理。
(5) 对光滑后的所有多边再进行一遍循环求交,以确保由于求凸包过程中两个距离很近的多边形有相交的情况。
经过以上处理,就完成了离散点所形成的边界提取。其流程图如图 2。

|
图 2 边界搜索流程示意 |
经过边界搜索,此时边界已经确定。为了确定无效值是无降水资料还是遗漏降水资料。本文站点数据做了如下处理。因为边界内的站点的值并非都是有效值。非有效值(或无效值)并不意味着这个站点的降水量为零,而是表示该站点的降水量未被记录下来或其他原因不能被应用。所谓数据插补是指对一定区域内的气象站点的空缺的值和无效值的处理。数据补差的基本原理如下:
首先在一个多边形(polygon)中查找无效值并添加到无效值(novalue)点集中,同时把有效值点放到有效值(value)点集中;
其次确定缓冲区的距离d,这里根据最大最小距离的方法来设定。
(1) 计算出有效值点集(value)中的第i个点到无效值点集(novalue)中其他测站之间距离中的最小值di。
(2) 取所有的di中最大的距离作为缓冲区距离d。
最后,根据缓冲区距离d,对多边形(polygon)中的无效值点集(novalue)的所有站点做缓冲区分析,此缓冲区分析是为了确定插值的边界问题,确保插值范围的准确性。计算落入该缓冲区内的有效值点集(value)的测站数目。如果数目大于或等于1,就认为该测站降水量是漏记,用落入该缓冲区中有效值点集(value)的平均值代替,反之,则认为该站点无降水。
3.3 核心算法MCressman的核心算法的主要步骤如下:
(1) 获得分级的个数(n)。对于降水来说就是分为小雨(1~9.9mm)、中雨(10~24.9mm)、大雨(25~49.9mm)、暴雨(50~99.9mm)大暴雨(100~250mm)、特大暴雨(>250mm)这六个级别,各级值分别为1,10,25,50,100,250。
(2) 计算权重Wijk。用Cressman方法计算出权重Wijk,这是MCressman对Cressman进行优化关键步骤。MCressman要对不同的级别按级别的大小给以限制,即级别越高其权重随着站点与分析格点距离的增加衰减越快。
| $ {{\rm{W}}_{ijk}}: = {\rm{W}}_{ijk}^{\left( {2 + a} \right)\left( {6 + 2a} \right)} $ | (4) |
其中a表示的是分级的序号,且a=1,2,…,n。“:=”表示替代。这种变化呈渐进趋势,能够更接近于真实的状态。实际意义就是同一降水量在图中可以表现出不同级别的范围和层次。
(3) “孤点”权重的处理。分析格点(i,j)时,在最大步长范围内找出参与插值的“孤点”,以便单调处理。即在5个步长的资料扫描中,若最小步长中已有资料,随着步长的增大,资料数没变即认为是“孤点”,如果是孤点该点的权重在(2)的基础上进一步降低。
| $ {{W}_{ijk}}_{:}=W_{ijk}^{2} $ | (5) |
这样就会使孤点的范围进一步缩小。使插值出现良好的视觉效果。
(4) 得到分级的格点分析场。把上面的权重参与到Cressman的插值计算中,计算出第m级别的相应格点的值Gm。
(5) 获得综合分析场。把所有级别的分析场合成一个综合分析场。由于MCressman是分级的,而且是分析低级别时就会包含有高级别的数据,所以在进行格点值的合并时一定要做比较,并遵循格点值大覆盖格点值小的原则。
如果(G[j] < Gm[j])则G[j]=Gm[j]。其中G[j]表示总的格点的值,Gm[j]则表示分级的格点的值。
其流程见图 3。
|
图 3 插值过程流程示意 |
格点的光滑主要采用的是九点光滑,其基本原理是对任意一格点周围的八个点和该格点本身的值求均值,再将其值赋给该格点,起到一定的滤波作用,达到图形边界光滑、美观的效果。同时,为了保证数据的临界值不会丢失,对格点值进行了分级光滑,其原理是对任意一级别的任一格点周围的八个点进行判断,如果判断结果存在无效值,就将该格点的值赋予无效值点,然后再将九个点的均值赋予该格点。
4 应用实验实践中,利用VC6.0实现了MCressman算法,并与传统Cressman算法进行了对比实验分析。实验选用了2007年10月12日08时至2007年10月13日08时的24小时降水量实况观测数据,观测站(离散点)个数为430个。其中在实况观测数据中,重庆出现了一个观测值为大雨量级(值为25mm)的站点,而在云南省与海南省分别出现了一个观测值为暴雨量级(50mm)的站点。Cressman算法和MCressman算法采用的步长均为1、2、4、7和10。图 4为Cressman算法插值生成的色斑图,图 5则为MCressman插值算法生成的色斑图。从图 4、5对比分析,没有改进的Cressman插值过程损失了云南省与海南省的暴雨级别的站点以及重庆的大雨量级的站点,而且内蒙古的大雨量级的站点在插值后的分布图呈圆形,效果不理想。青海省西南部、西藏的东南部还有碎块出现,观测文件中这些碎块所在区域的站点值都是小于1的。而MCressman插值分析结果形成的分布图,不仅保证了数据的准确性,也达到了良好的图形质量与视觉效果,很好地弥补了Cressman算法的不足。
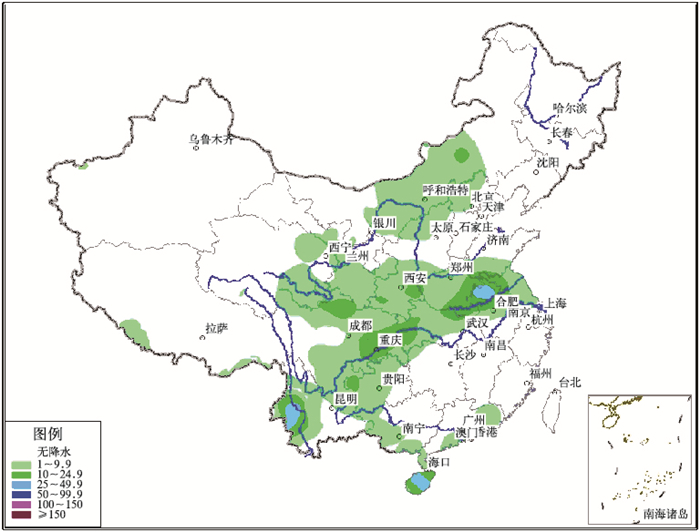
|
图 4 Cressman的插值结果 |
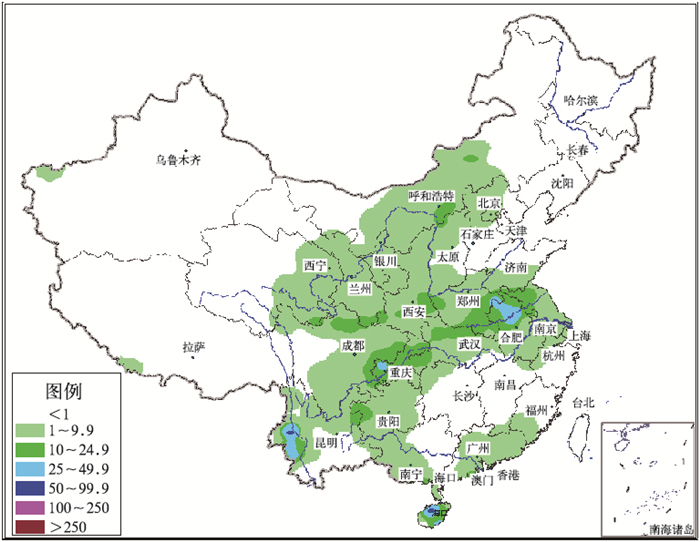
|
图 5 MCressman的插值结果 |
本文在分析各类常用插值算法的基础上提出了一种基于Cressman方法的优化算法,并对改进插值算法的关键技术问题进行了详细讨论。实验表明,MCressman算法有效地保证了气象降水色斑图的精确性和美观性的要求。在业务系统中得到了很好的应用,从而使每天的降水量实况图的生成体现了完全的自动化业务运行能力,大大地节省了人力,比常规人工分析的雨量图所含信息更多,减少了人为随意性,增强了插值的精确性和客观性。该算法虽然是针对降水描述的,但也同样适用于其他气象要素的分布图的分析制作。
吴焕萍, 罗兵, 王维国, 等, 2008. GIS支持下的决策气象服务系统建设[J]. 应用气象学报, 19(3): 380-383. DOI:10.11898/1001-7313.20080316 |
黄杏元, 马劲松, 汤勤, 2001. 地理信息系统概论[M]. 北京: 高等教育出版社, 93-103.
|
邬伦, 刘瑜, 张晶, 等, 2001. 地理信息系统原理方法和应用[M]. 北京: 科学出版社, 178-192.
|
赵天保, 艾丽坤, 冯锦明, 2004. NCEP再分析资料和中国站点观测资料的分析与比较[J]. 气候与环境研究, 6: 278-294. |
冯锦明, 赵天保, 张英娟, 2004. 基于台站降水资料对不同空间内插方法的比较[J]. 气候与环境研究, 6: 261-277. |
王跃山, 2001. 客观分析和四维同化——(II)客观分析的主要方法(1)[J]. 气象科技, 1: 1-9. |
GEORGE P, 1959. CRESSMAN.AN OPERATIONAL OBJECTIVE ANALYSIS SYSTEM[J]. Monthly Weather Review, 87(1): 367-374. |
朱海燕. GIS空间分析方法在热带气旋研究中的应用[D]. 华东师大硕士学位论文, 2005, 1-54. http://cdmd.cnki.com.cn/Article/CDMD-10269-2005085836.htm
|
张立祥, 陈力强, 周小珊, 等, 2001. 中尺度数值预报中不同初值方案的检验对比[J]. 气象, 27(7): 8-12. DOI:10.7519/j.issn.1000-0526.2001.07.002 |
周青, 赵凤生, 高文华, 2008. 中国实测地表温度和地面气温对比分析[J]. 气象, 34(2): 83-91. DOI:10.7519/j.issn.1000-0526.2008.02.012 |
 2009, Vol. 25
2009, Vol. 25