风是自然界中随机性最强、受环境影响最为敏感的因子之一。在风能开发中,必需以适当的现场风观测为基本依据。我国在2002年10月1日实施的中华人民共和国国家标准《风电场风能资源测量方法》GB/T18709-2002[1],对测风站的位置、测量参数、采用的仪器及安装要求、数据收集整理方法和格式等都做了明确规定,为我国风电开发建设起了重要的指导作用。随着我国风电建设的快速发展,风电场选址不只在较平缓的平原、戈壁,还遍布于丘陵、山地、海岛等多种复杂地形上,开发成本、资源测量计算难度和投资风险均大大增加,因而,对风电场风资源测量、计算和评估的要求应更精细、严谨和准确。据专家统计,目前我国已建成投产的若干个风电场的实际运行效益比项目前期预期效益差20%~30%[2],由于风电场前期风资源测量的设置和操作不尽合理、观测数据质量和计算误差缺乏质量控制等导致了风资源评估产生较大误差,从而成为项目前期效益预评估与实际运行结果相差甚远的主要原因之一。
气象部门历来十分重视观测数据的准确性、代表性和可靠性,目前全国气象系统使用的“全球观测资料质量监视评估系统”利用资料同化技术和质量控制技术来排除观测资料中的可能错误[3], 以使气象观测资料质量达到气象业务应用的要求;气象科研和业务观测中所有的气象观测仪器均按照国家相关规范要求进行检测、标定后才安装运行,尤其对随机性较强的风测量仪的精度标定提出了更合理、更具操作性的方法[4]。但由于风能资源观测评估目前尚未完全纳入气象行业技术管理,对风能评估中可能出现的仪器检定、风观测设置和计算精度问题,目前尚缺乏系统研究总结。
本文根据多个复杂地形风电场观测操作实践和观测数据的计算分析,主要针对位于复杂地形和典型季风气候区的风电场,探讨分析影响风资源测量精度的因子、解决方法和采取的措施以及风资源测量、计算过程中可能存在误差的程度等,以期对风电场建设最基础的现场风资源测量和基础数据的质量保障、计算误差估计提供参考。
1 影响风资源测量计算精度的因子影响风资源测量数据质量的主要因子有:复杂地形观测点所能代表的范围的局限性、仪器性能限制、设备安装质量和仪器设置等。
1.1 地形地貌风电场地形地貌(下垫面)的复杂程度直接影响了风资源测量和计算的难度。一般来说,地形比较平缓、地貌比较一致的风电场(如平坦的戈壁、平原、海滩平缓顺直的海岸带等),风场受下垫面的强迫作用较小,可以少量的测风点代表较广阔的区域,资源测量精度较少受地形地貌影响。而位于复杂下垫面的风电场,如山地、丘陵、河谷、凹凸曲折的海岸和海岛等,受复杂下垫面的动力强迫和不均匀的热力影响,局地风场将产生很大的改变,尤其当有剧烈的天气系统(如,台风、强冷空气)经过时,将导致局地风的微观特性和空间分布均发生更为复杂的变化[5-7]。
对于地形起伏的山地,气流被改变的形态不仅与山形有关,还与当时的天气系统结构、主导气流速度有关。气流遇到范围不大的山脊或孤立的山峰时,大部分气流从山的两侧绕过,小部分从山顶越过;气流遇到高大的山脉时,大部分气流将被迫从山顶越过,这时在迎风坡的气流受到阻挡,将在某个高度区域产生上升式回旋气流,背风坡则由于气流辐散而在某高度区域产生下沉式回旋气流[8],产生回旋气流的区域不但导致风速减小,而且还会产生较强烈的湍流,若风机叶轮恰好处于这一区域,不但发电量减少,而且还将加速风机的疲劳损坏。
对于凹凸曲折的海岸和海岛风电场,其风场除了受地形起伏的影响外,还受着热力性质差异很大的海陆下垫面影响,从而产生了海陆风环流,海陆风在近地层某高度处交汇切换,也将导致该高度层的风速减小,紊流增加。根据文献[9-10]的观测研究,海陆风高度有时在100m以下的近地浅层中,若风机轮毂恰好处于这种海陆边界层常出现的高度,其后果与山地涡旋区相似。在平缓的海岸地区,测风高度足够高时,通常可以通过观测,基本摸清海陆风的交汇切换高度是否在轮毂区域,但当海岸凹凸曲折和海岛面积较大时,受地形影响,海陆风交汇切换层的高度将很不均匀,观测点的代表性大为下降。
可见由于下垫面复杂,每个观测点的代表范围十分有限,测风站数量太少或设置不合理将直接影响风电场风资源测量的质量和精度。
1.2 测风仪性能目前风电场测量使用的测风仪多为风杯风速计,试验表明[11],由于风杯风速计的惯性特征,致使其在环境风速由低风速转变为高风速时,仪器的跟踪能力优于环境风速由高变低时,从而使仪器显示的平均风速略高于实际的平均风速,此现象称为风杯风速计的过高效应。因此在风速稳定性较差的地区,由于风杯风速计的惯性特征可能影响风资源测量的精度。
复杂地形上的风矢量变化比平缓地形要剧烈得多,由于地形影响,可能造成更强烈的上升或下沉气流,风向的稳定性也较差。根据张蔼琛的研究[11],风杯在风矢量的攻角不大时,完全没有余弦分辨能力,导致水平风速测量偏高;由于风杯风速计测量的是风速模量,与测量风速矢量的风速计(如:超声测风仪)对比,在风向的脉动较大时,导致风速测量值大于实际风速。在贵州省的一个典型山地采用三维超声测风仪和风杯风速计的对比观测也证实了这一点。三维超声测风仪的实地观测数据显示,在对风力发电具有代表意义的7~12m·s-1风速区间,地形影响产生的垂直气流速度在-1.3~1.8m·s-1,随地形而变化的风攻角范围在-9°~11°,山地风场的强烈垂直运动,将导致风杯风速计的过高效应,超声和风杯式风速仪的逐日平均风速对比观测显示,风杯式风速仪测量的日平均风速较超声风速仪平均偏大6%。
因此,复杂地形风电场,尤其在起伏较大的山地测风时,应注意可能由于风杯风速计的不适应性而导致风资源的过高估算。
1.3 设备安装对于测量设备的安装,GB/T18709-2002做了较为详细的规定,但许多项目的设备安装仍存在较多问题,并且这些问题都比较隐蔽,难以发现和校正。根据近几年的大量调查和实际经历,总结影响观测数据质量的设备安装问题主要表现在:
① 观测塔的垂直度和仪器的水平校准不规范。观测试验发现,当测风塔歪斜或仪器安装不水平时,测量的风速值均小于实际风速,这种观测误差随着离垂直或水平的偏差角度的增大而加大。
② 仪器信号线捆扎不牢固。由于仪器信号线的自身重量和环境风的影响,信号线捆扎的间隔距离不宜太远,应越往高处捆扎密度越大。信号线捆扎不牢固可能导致信号传递不良或时断时续,这种故障出现时,观测数据并不会完全消失,而是明显地偏小,所以这种数据错情往往很难从观测中被发现,从而导致观测数据精度下降。
1.4 仪器设置方位GB/T18709-2002规定测风传感器应安装在主风向的方位一侧,以避开塔体对风的影响。风洞试验、实际观测和数值模拟均证明了塔体对风的影响十分明显。例如胡非等根据中国科学院北京325m高气象塔近10年的梯度观测资料分析和CFD模拟试验发现,塔体对风速的影响程度随高度和方位而变化,位于塔的背风面风速相对于迎风面的差值可以达到23%~30%[12]。虽然风能观测塔一般较细小,但测风传感器设置的方位仍是影响测风精度的重要因子。
2 风资源测量的精度控制 2.1 复杂地形测风站选址显然,复杂地形风电场测风站的设置数量需要比简单地形适当多一些,复杂地形风电场更需要仔细、综合考虑每一个测风点的代表性和必要性,对于起伏较大、山脉走向多变和海岸线弯曲的场地,测风点除了测量风资源的大小外,还应考虑地形和季节代表性,尽可能测量判别局地的气流回旋区。对复杂地形风电场测风站选址建议至少应遵循以下原则:
① 优劣均选原则
至少应在该风电场风资源可能最好的地点和风资源可利用的下限区域,均设置测风站,以便较全面地掌握该风场的全貌。
② 类型代表性选站原则
对于山脉或海岸线走向相似或山体高度、形状、下垫面性质较一致的地形,应选取具有类型代表性的测站,以点带面,以少代多,可以大为节省观测工程开支。
③ 临界区选取原则
在山地中可能安装风机的最低高度上选取临界测风站,测量出风机排布的下限位置。根据目前风电场建设成本和上网电价现状,建议临界站可设置在估计平均风功率密度为200~250W·m-2的位置上。
④ 风特征选取原则
我国大部分地区为季风气候区,风向的季节性差异明显,对山地来说,冬季为迎风面的山坡,在夏季很可能成为了背风面,因此,需要在可能具备利用价值的季节性的迎、背风坡均设置观测站,以测量迎、背风向的季节性差异。
⑤ 工程可操作性选取原则
风资源较好的山地,大都是人烟稀少,难以到达的偏僻地区,前期测风站选取还应考虑人员比较容易到达,测风活动具备较好的可操作性,这是保证观测数据完整率的重要前提。
2.2 仪器选型和设置鉴于风杯风速计的惯性特征,风速多变和地形复杂的地区,尽量选择性能较好的测风仪,有条件时,可以在具备地形代表性的观测塔上,同时安装超声测风仪进行对比观测,为数据校准订正提供依据。
为了尽量避免塔体对测风精度造成影响,建议在季节风影响较明显的地区,至少在轮毂高度的两个季节性迎风面上均安装测风仪,以便有选择地利用实测数据。
3 风资源计算的误差估计 3.1 仪器系统误差的订正和偏差估计由于每个风速计在制作过程中的杯形、惯性特征等微小差异,可能导致该风速计测量的风速值与真实风速产生偏差,大量试验证明,这种偏差通常以系统性形式表现,并在风洞中可以测量出来(不同品牌的风速计,系统偏差的趋向有明显差异)。因此,在风电场测风观测之前,对风速仪进行风洞测试,给出详细的订正曲线和订正参数很有必要。
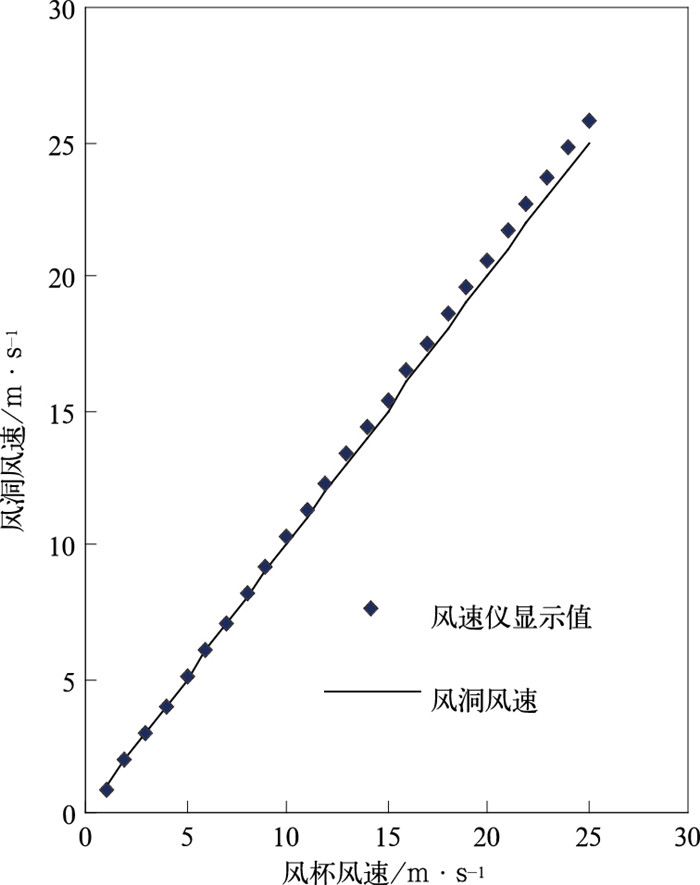
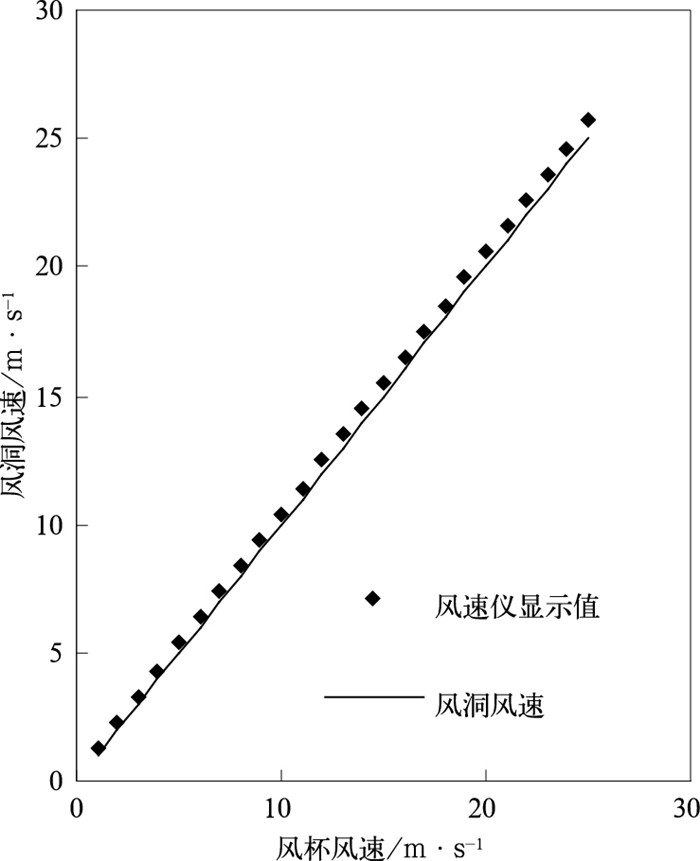
图 1、2是某两个风速仪进行风洞测试后,给出的检定校准曲线。
|
图 1 1号风速仪订正曲线 |
|
图 2 2号风速仪订正曲线 |
风速仪检定校准方程为:
| $ {V_z} = a + b{V_c} $ |
式中,Vz为标准风洞风速(即风速真值),Vc为风速仪显示风速(即实际观测值),a、b为订正系数。
实际计算中应注意,对于仪器系统误差的订正需要将风洞测试给出的订正方程引入原始测风数据中处理,以尽可能提高测风数据精度。
3.2 仪器导致的风参数误差估计① 测风仪的相对误差
为了定量估计目前较普遍使用的测风仪系统误差的影响程度,在此统计每个风速仪的平均相对偏差,由下式计算:
| $ \begin{array}{l} R = 100 \times \frac{1}{n}\sum\limits_{i = 1}^n {\frac{{|{V_{{Z_i}}} - {V_{{C_i}}}|}}{{{V_{{Z_i}}}}}} \\ \;\;\;\;\;\;\;\;\;\;\;i = 1, 2 \cdots, n \end{array} $ |
式中,R为仪器的平均相对偏差,n为样本数。
近两年,在广东省气象计量检定所标准风洞测试了近百个风速仪,发现目前普遍采用的进口风速计的相对偏差在1.6%~5.25%之间,平均为3.05%。
② 风资源参数误差估计
以广东某风电场的实际测风计算为基础,给出由于仪器的系统误差而导致风资源参数偏差的一个实例。
根据实际应用,选取安装在轮毂高度附近的测风仪,计算因仪器本身的偏差,可能导致的实际风速误差和年风功率密度的误差(见表 1)。
|
|
表 1 仪器系统偏差导致的实际风速和风功率密度误差值 |
表 1中的实例显示,由于测风仪的此项系统偏差,可导致轮毂高度附近的年平均风功率密度误差在5%以上,最大达13.8%。这一误差,对风电场的投资决策可能产生重要影响。
3.3 缺测数据的订正误差由于仪器故障、雷击、冰冻等不可抗拒的天气灾害和难以预见的其它原因影响,实地风测量往往存在数据缺漏,因而必然要进行数据的插补和订正,以尽可能保持风计算序列的真实性和完整性。
在实际操作中通常会选取与缺测点相近、下垫面性质相似,且可通过一定的相关分析检验的其它观测点的同期实测数据建立相关方程,而且很多人相信,采用的同期实测数据序列越长,订正效果越好,这在风向和风速的季节变化不太大的地区是可行的,但在季风气候区和由于地形地貌影响致使风的季节变化较大的地区,可能会由于对参与订正的基础数据样本序列的选取不当,而严重影响被订正的数据序列质量。下面给出的典型例子可以看出这种误差对风资源计算精度的影响程度。
以位于广东沿海的某风电场的实测资料为例。该风电场属海岛山地地形,风的季节性变化明显,冬季以东北偏北风为主,夏季盛行东南风。该风电场实地观测时间为2005年5月1日至2006年4月30日。在该项目中,选取两个观测塔完整1年的实测资料进行试验计算。两个试验观测塔设置情况见表 2。
|
|
表 2 两个测风塔设置和观测环境描述 |
设定B塔轮毂高度层(60m)在冬季风控制季节的12月份和在夏季风控制季节的6月份的数据缺测,以A塔轮毂高度(60m)同期的实测资料进行订正插补,然后用B塔缺测月份的实测资料验证其误差。
在此,用于与B塔进行相关检验的A塔的数据序列选择采用3种试验计算方案:
① 以A、B塔全年(除缺测月以外)的同期观测数据进行相关检验;
② 以A、B塔冬季月份(除缺测月以外)的同期观测数据进行相关检验;
③ 以A、B塔夏季月份(除缺测月以外)的同期观测数据进行相关检验。
其线性回归表达式:
| $ Y = aX + b $ |
式中a、b为回归系数,X为参与订正的实测风速,Y为被订正的缺测风速, 为了检验拟合方程的回归效果,检验统计量:
| $ F = \frac{{{R^2}}}{m}/\frac{{1 - {R^2}}}{{n - m - 1}} $ |
式中R为相关系数,n为样本量,m为自变量个数,通过给定一定的显著性水平,检验F值。相关检验和回归参数见表 3、4。
|
|
表 3 3种订正方案的线性回归效果 |
|
|
表 4 3种方案的订正结果和精度 |
表 3显示的相关检验结果显示,无论缺测月份在冬季的12月还是夏季的6月,3种计算方案的相关系数均高达0.9以上,并且均可以通过0.01的显著性检验。
以3种订正计算方案分别计算被订正月份的逐时平均风速,并以此序列计算被订正月份的平均风功率密度,3种订正计算方案结果列于表 4。
表 4中的订正参数显示,在假设缺测的月份为12月时,以与之同处于冬季风月份的11、1、2月的同期观测数据为订正样本,得到的被订正(12月)月的平均风速与实测风速只相差0.1m·s-1,月平均风速相对误差只有1%,该月的平均风功率密度订正值的相对误差只有3.9%;而以全年(不含缺测月份)的数据序列的订正结果,虽然使用的同期观测数据样本更多,但被订正月份的平均风速相对误差为6.9%,平均风功率密度订正值的相对误差达到了23.6%,远远大于同季节月份的订正方案;以与缺测月份12月不同季节的5、6、7月的同期实测数据进行订正时,尽管其相关系数也高达0.91,并且也通过了0.01的显著性检验,但被订正(12月)月份的平均风速相对误差达14.9%,平均风功率密度订正值的相对误差高达41.6%。
假设缺测的月份在6月的订正结果也有类似特征,3种方案的月平均风速订正的相对误差分别为1.3%、11.5%、19.2%,平均风功率密度订正值的相对误差分别为6.7%、28%和53.4%,具有明显差异。
对比分析表 4中的订正参数还发现,缺测时段处于大风时期的冬季时,以全年或处于小风季节的夏季同期观测数据进行订正,其结果均小于实际观测值,风速差异越大,其订正值偏小误差越大;而缺测时段处于小风时期的夏季时,以全年或处于大风季节的冬季同期观测数据进行订正,其结果均大于实际观测值,风速差异越大,其订正值偏大的误差越大。
可见,在季风气候区、复杂地形和风的年变率较大的地区,缺测数据的插补和订正应尽量选取同季或同主导风向的同期观测时段数据,作为缺测数据插补和订正的基础数据。
4 结语(1) 复杂地形测风站的空间范围代表性较小、仪器性能的局限性、设备安装质量和仪器设置不合理等是影响风资源测量和计算精度的主要因子。
(2) 对风电场观测数据和计算质量进行精度控制的主要措施包括:测风站选址至少应遵循优劣均选、类型代表性、临界区选取,并根据当地风特征和工程可操作性进行选址等5项原则;根据仪器的适用性和风场特征进行合理的仪器选型和设置等。
(3) 大量的实测和风洞检验显示,目前我国风能观测较普遍采用的进口风速计的测量相对偏差在1.6%~5.25%之间,随之可导致轮毂高度附近的年平均风功率密度误差在5%以上,最大达13.8%。
(4) 在季风气候区、复杂地形和风的年变率较大的地区,缺测数据的插补和订正应尽量选取同季或同主导风向的同期观测时段数据,作为缺测数据插补和订正的基础数据,否则可导致平均风功率密度相对误差达20%~50%。
中华人民共和国国家标准《风电场风能资源测量方法》[M]. GB/T18709-2002.
|
贺德馨, 依靠科技进步发展中国风电产业[M]. 中国风电发展论坛.
|
陶士伟, 张跃堂, 陈卫红, 等, 2006. 全球观测资料质量监视评估[J]. 气象, 32(6): 53-58. DOI:10.7519/j.issn.1000-0526.2006.06.009 |
李国森, 敖振浪, 2006. 风速仪在风洞检定中的阻塞修正[J]. 气象, 32(9): 67-70. DOI:10.7519/j.issn.1000-0526.2006.09.011 |
宋丽莉, 毛慧琴, 植石群, 等, 2005. 登陆台风近地层湍流特征观测分析[J]. 气象学报, 63(6): 961-965. |
Richards P.J, Fong S, Hoxey R.P, 1997. Anisotropic turbulence in the atmospheric surface layer[J]. Journal of Wind Engineering and Industrial Aerodynamics, 69-71: 903-913. DOI:10.1016/S0167-6105(97)00216-X |
宋丽莉, 毛慧琴, 钱光明, 等, 2006. 热带气旋对风力发电的影响分析[J]. 太阳能学报, 27(9): 961-965. |
潘守文, 等, 1994. 现代气候学原理[M]. 北京: 气象出版社.
|
张铭, 张立风, 颜兆辉, 等, 1999. 海陆风环流的计算方法[J]. 大气科学: 693-702. DOI:10.3878/j.issn.1006-9895.1999.06.06 |
周伯生, 汪永新, 俞建国, 等, 2002. 广东阳江沿海地区海陆风观测结果及其特征分析[J]. 热带气象学报, 18(2): 188-192. |
张蔼琛, 2000. 现代气象观测[M]. 北京: 北京大学出版社.
|
胡非, 程雪玲. 北京325m气象塔塔体对测风影响的数值模拟[J]. 气候与环境研究, (待发表). http://kns.cnki.net/KCMS/detail/detail.aspx?filename=qxkj201404002&dbname=CJFD&dbcode=CJFQ
|
 2009, Vol. 35
2009, Vol. 35