2. 山西省气象局
2. Shanxi Meteorological Bureau
太阳辐射是地球表层能量的主要来源,是气候形成的最主要影响因素。气候的变迁与到达地表的太阳辐射能量的变化关系极为密切,相应地太阳辐射的时空变化直接影响着一切与气候有关的资源的空间分布。虽然太阳辐射能量的时空分布主要决定于区域地理纬度,但区域的高度、坡度、坡向以及遮蔽度对局地太阳辐射能量有着重要的影响,由于地面起伏变化造成局部地面接收太阳辐射量存在很大的差异,是造成局部小气候特征差异的主要原因。同时,也直接影响到诸如土壤水分、地面无霜期以及作物生长适宜性程度等多项重要的生态与农业生产气象指标。由于太阳辐射观测设备具有设备复杂、成本费用高、观测密度远小于气象要素的观测密度等方面的缺憾,而采用简单的空间内插或外推技术又不可能合理地揭示太阳辐射的空间分布特征。因此在研究局地气候问题时,应充分利用数字高程模型(DEM)数据以及GIS空间分析方法,建立一个合理的太阳辐射空间模型,实现对地面所获得太阳辐射量的数值模拟。
有关太阳辐射数值模型的研究前人做了大量卓有成效的研究工作。我国学者傅抱璞对于任意地形条件下太阳辐射进行了开创性研究[1-4],张雪芬、李占清、朱志辉、林正云等学者根据我国的实际情况分别对太阳总辐射及其分量计算模型进行了深入细致的研究[5-8]。国外Dozer提出了利用数字高程模型模拟太阳辐射的方法,Gilabert和Civco探讨了任意地形条件下的辐照入射度模拟[9-12]。我国学者李新、曾燕、杨昕、何洪林等针对各自的研究区域,利用不同分辨率的DEM数据进行了太阳辐射模拟研究[13-19]。然而建立在DEM数据基础上的太阳辐射数值模拟会受到DEM分辨率的影响而有所变化[19],因此太阳辐射的数值模拟应针对研究区域的地形特征进行,以期更好地体现太阳辐射在局地的再分配与小气候的差异性。
本文在借鉴国内外已有的太阳辐射计算模型的基础上,以地形复杂多变的山西高原为研究区域,采用美国航天飞机雷达地形测绘任务(SRTM)全球90m分辨率数字高程DEM资料,提取研究区域地理纬度、坡度、坡向等地形参数,建立区域太阳潜在总辐射计算模型,以纵跨山西南北的3个辐射观测站的太阳辐射日观测数据进行模型检验分析,研究由于地形起伏变化造成太阳潜在辐射能量在山西高原的时空分布规律,并分析了区域坡度、坡向对太阳潜在辐射的影响。
1 太阳潜在总辐射计算模型 1.1 太阳潜在总辐射地表接收的太阳辐射量主要受太阳几何因素、区域地形因素以及其间的云量和其他非均质性大气因素影响。太阳总辐射包括直接辐射、散射辐射以及由周围地形所引起的反射辐射。晴天无云条件下的太阳总辐射是地球表面可能接受到的太阳总辐射的最大值,即潜在太阳总辐射[18]。本文参照文献[18-21]的做法,将太阳总辐射分为太阳直接辐射、天空散射辐射和地表反射辐射三部分,即复杂地形条件下晴朗无云条件下地表潜在太阳总辐射:
| $ {I_t} = {I_s} + {I_d} + {I_r} $ | (1) |
其中Is代表太阳直接辐射,Id是天空散射辐射,Ir是地表反射辐射。
1.1.1 直接辐射地球表面任意坡面上太阳光线入射角i的瞬时直接太阳辐射Is是坡度、坡向、太阳赤纬、纬度、海拔高度以及大气透射率的函数,其计算公式[22]如下:
| $ {I_s}{\rm{ = }}{\mathit{I}_0}\cos i{\tau _b}g $ | (2) |
其中:I0=S0E0为大气上界垂直入射的太阳辐射强度,S0为太阳常数,取1367W·m-2;E0为地球轨道偏心率较正因子;τb为大气透射率(或大气透明度系数);g为地形遮蔽度因子。
坡面上太阳光线入射角i按下式计算:
| $ \begin{array}{l} \cos i = \left( {\sin \varphi \cos \alpha - \cos \varphi \sin \alpha \cos \beta } \right)\sin \delta + \\ \;\;\;\;\;\;\;\;\;\;\left( {\sin \varphi \sin \alpha \cos \beta + \cos \varphi \cos \alpha } \right)\cos \delta \cos \omega + \\ \;\;\;\;\;\;\;\;\;\;\sin \alpha \sin \beta \cos \delta \sin \omega \end{array} $ | (3) |
其中:α为坡度;β为坡向;ω太阳时角;φ为地理纬度;δ为太阳赤纬;时角ω=15·(T-12)描述太阳24小时的运行情况。
地球轨道偏心率因子采用下式计算:
| $ \begin{array}{l} {E_0} = 1.000109 + 0.033494\cos \theta + \\ \;\;\;\;\;\;\;\;0.001472\sin \theta + 0.000768\cos 2\theta + \\ \;\;\;\;\;\;\;\;0.000079\sin 2\theta \end{array} $ | (4) |
太阳赤纬采用下式计算:
| $ \begin{array}{l} \delta = 0.006894 - 0.399512\cos \theta + \\ \;\;\;\;\;\;0.072075\sin \theta - 0.006799\cos 2\theta + \\ \;\;\;\;\;\;0.00089\sin 2\theta \end{array} $ | (5) |
式(4)、式(5)中:θ为日角,θ=2π(N-1)/365.2422,N为天文日。
大气透射率按下式计算:
| $ {\tau _b} = 0.56\left( {{{\rm{e}}^{ - 0.56{M_h}}} + {{\rm{e}}^{ - 0.095{M_b}}}} \right) $ | (6) |
其中:Mh为一定地形高度下的大气量Mh=M0ph/p0,M0为海平面上的大气量,计算公式为
运算中需计算日出日落时角,按一定的时角间隔,计算后积分即可得出日辐射量。日出日落时角按下式计算:
| $ \begin{array}{l} {\omega _s} = \arccos \left( { - \tan \delta \cdot \tan \varphi } \right)\\ {\omega _r} = - {\omega _s} \end{array} $ | (7) |
其中:ωr为日出时角;ωs为日落时角,日出和日落时间间隔为日长。
1.1.2 散射辐射在晴朗无云条件下天空的坡面上散射辐射采用下式[22]计算:
| $ {I_d} = {I_0}{\tau _d}{\cos ^2}\frac{\beta }{2}\sin \alpha $ | (8) |
其中, τd为散射辐射透明系数,作为均质散射其与直接辐射之间存在线性关系。
| $ {\tau _d} = 0.271 - 0.294{\tau _d} $ | (9) |
反射辐射与地表的坡向、坡度以及地表的反射率有关。假设反射地表是一个朗伯体,得出反射辐射的计算公式[22]为:
| $ {I_r} = r{I_0}{\tau _r}{\sin ^2}\frac{\beta }{2}\sin \mathit{a} $ | (10) |
式中:r为地表反射率;τr为反射透明度系数,τr=0.271+0.706τb。
1.2 模型建立 1.2.1 地形遮蔽因子数字高程模型DEM为栅格单元太阳辐射的计算创造了重要的条件,能够利用光线追踪算法计算地形遮蔽信息,本文地形遮蔽的计算采用光线追踪算法[17],搜索入射路径上所有格网点,若某格网点高程与计算格网点高程之间的高度角大于该入射路径上的太阳高度角,则这是一条可遮蔽路径,记di=0;否则di=1。分别计算不同时刻的di值,判断每一积分时段内是否可照,地形遮蔽因子g=(di-1+di)/2。
1.2.2 计算流程为了便于计算机编程实现,将每日的可照时角离散化,即划分成一系列时间单元,模拟计算每一时段内的辐射量,最后累加求和。主要过程如下:
(1) 以DEM为数据基础,提取纬度模型、数字坡度模型、数字坡向模型等数字地形信息。
(2) 由公式(7)计算太阳日出、日落时角,按照精度将日长分成若干时间段,计算时设时间步长为10分钟。
(3) 从日出开始,结合各时段内的地形遮蔽系数,由公式(2)、(8)、(10)分别计算每一个时段内太阳辐射量。
(4) 对各时段内的太阳辐射量进行累加求和得出一天内的太阳辐射量,依次类推,可以求出各月、季、年的太阳辐射总量。
2 研究区域及数据处理 2.1 研究区域本文以位于黄土高原东部、相对东西两侧整体隆起的山西高原为研究区域。研究区域介于110°14'42〞~114°33'17〞E、34°34'58〞~40°44'30〞N之间,区内自然环境多样,有山地、高原、丘陵、盆地,其中包括山地、高原、丘陵在内的整个山区面积占土地总面积的72%以上。大部分地区海拔在1000m以上,与其东侧海拔不到100m的华北大平原和西侧海拔1000m左右的黄河峡谷两岸的高原相对比,呈现强烈的整体隆起态势。
2.2 数据处理研究区域DEM数字模型为美国航天飞机雷达地形测绘任务(SRTM)全球90m分辨率数字高程DEM资料,用于计算提取区域经度、纬度、海拔、坡度、坡向以及地形遮蔽模型等地形参数。
关于模型计算中太阳反射辐射计算所用的地表反射率数据采用MODIS反射率数据集。本文所利用的数据类型为NASA提供的2005年MODIS250m分辨率8天合成地表反射率数据集。应用过程中,首先对质量系数较低的数据采用相邻时间、相邻网格的数据进行插值,然后将数据结果按照本文DEM分辨率90m要求,采用空间数据重采样到要求的空间分辨率。
为对模型计算的太阳潜在总辐射结果进行检验分析,应用纵跨研究区域南北的3个气象站(侯马、太原、大同)的2001—2005年近5年逐日逐时太阳总辐射观测资料以及总低云量观测资料作为模型的检验数据。
3 研究结果与分析 3.1 模型检验分析选取研究区域内的3个气象站2001—2005年的逐日太阳总辐射资料作为模型的检验数据,样本选取中参考应用各气象站定时观测的总低云量观测资料,利用5年中每日08和14时总低云量均为0的观测日数据最大值作为代表晴空无云条件样本与模型计算数据进行比较,以此来验证模型的准确性与适用性。所用3个气象站的地理信息见表 1。
|
|
表 1 气象观测站地理信息 |
经过对3个气象站太阳辐射观测值与模型模拟值的比较分析,分别计算其均方根偏差(RMSE)、平均偏差(MBE)、绝对偏差(MABE)以及平均绝对误差值(MAPE),统计结果见表 2。从3个站点模拟值与实测值的误差分析结果可以看出:3个站的MBE值均大于0,表明模拟值大于观测值;从MABE值的大小来看,3个站的结果在1.38~1.77MJ·m-2·d -1之间,RMSE在1.75~2.26之间,MAPE在7.9%~11.04%之间,说明模拟结果与观测值的相对误差在10%左右。各站误差分析共性之处表现在,所有分析结果都表现出由北及南逐渐增大的趋势。
|
|
表 2 3个站的模拟统计值站名 |
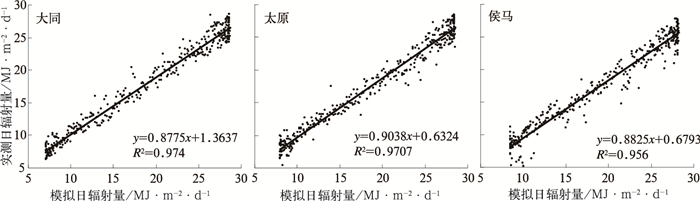
对模拟得到的逐日太阳辐射与实际观测值进行相关分析(见图 1)可见,二者的相关性均达到了极显著相关水平,3个观测点的相关系数为0.95~0.97之间,表明模型可用于区域太阳潜在总辐射的模拟计算。
|
图 1 模拟值与实测值相关结果 |

|
图 2 3个站点太阳日总辐射的模拟曲线与验证曲线图 |
分析模型计算的地面晴空条件下的太阳辐射日变化以及实际观测结果可以看出, 模型计算得到的晴空辐射值与实际观测值基本一致。但由于大气成分、大气中水汽含量以及大气悬浮物含量的差异, 造成大气对太阳辐射的吸收和散射不同, 影响了到达地面的太阳总辐射。由北及南3个测站的误差分析以及相关分析清楚地表明了此间的差异。山西高原由北及南大气中的水汽逐渐充沛,大气透明度逐渐变差,而模型中的大气透明系数选取由于缺乏相关数据而无法反映出其间的变化,从而导致误差逐渐增大;另外模型模拟值总体上大于观测值,说明引用的大气透明度系数存在偏高的可能,因此对于区域的太阳潜在总辐射进行模拟计算时,应结合相关观测数据(诸如水汽含量、气溶胶厚度以及气象资料[23]等)对大气透明度系数进行必要的校正。同时山西区域较重的环境空气污染也是造成模型计算结果偏高的一个原因。
3.2 太阳潜在总辐射时空分布特征根据模型计算的90m分辨率地形下的山西高原逐日太阳潜在总辐射空间分布结果,统计合成得到各季及年的太阳潜在总辐射量,将辐射量值按照一定的间隔进行分级,得到潜在太阳日辐射量空间分布图。图 3为年均及6月、12月代表月的潜在太阳辐射量日均值空间分布图。

|
图 3 山西高原太阳潜在总辐射空间分布 |
由计算结果统计得到区域年太阳潜在总辐射量日均值为19.60MJ·m-2·d-1,从空间分布上看,区域年太阳潜在总辐射值日均值在2.19~25.82MJ·m-2·d-1之间,基本上由北到南逐渐增大,但是纬向分布特点不是十分明显,但是随着地形、地貌部位的不同,太阳潜在年辐射量的空间分布差异相当显著,高辐射量值主要出现在阳坡,一般以山脊为辐射量的分界线。如区域内地形较为复杂的吕梁山、太行山、恒山较大,而其间雁行排列的几个山间盆地相对较小,区域太阳潜在总辐射的空间分布差异较大,空间分布的标准差为1.69MJ·m-2·d-1,高于周边区域,表明山西高原太阳辐射的空间变异性较大。受坡向、坡度和地形遮蔽因子影响,山区平川间的辐射差异远大于纬向间分布差异,太阳潜在辐射表现出明显的非地带性分布特征。
依据模型计算结果统计区域各月太阳潜在总辐射变化情况见表 3。可看出太阳辐射有明显的月间变化。就整个山西高原平均而言,各月中6月的太阳潜在辐射量最大,12月最小;按照季节划分,太阳潜在辐射量的大小依次为夏季>春季>秋季>冬季,表现出太阳潜在辐射的季节分布不对称性;标准差体现了数据间的离散和差异程度,6月的标准差最小,1月的标准差最大,说明地理因子(纬度)和地形因子(坡度、坡向、地形遮蔽)在高太阳高度角情况下对太阳辐射影响较小。从不同季节太阳辐射量地理分布图上也可看出这点,夏季的6月太阳辐射量大、空间差异不大,空间分布图色调较为单一。而冬季太阳高度角较低、辐射量标准差大,地理、地形因子对太阳辐射的影响体现得比较明显。
|
|
表 3 山西高原各月潜在太阳总辐射特征统计(单位:MJ·m-2·d-1) |
为了分析区域地形因子对到达地面的太阳潜在总辐射量的影响,分别选取1年中6月和12月作为典型代表月份以及全年对不同坡度的阴坡(偏南坡)和阳坡(偏北坡)潜在太阳总辐射量进行了统计制图。表 4为不同坡度下阴坡、阳坡年均潜在太阳辐射量变化情况统计表。图 4为不同坡度下阴坡、阳坡潜在太阳辐射变化曲线(年均、6月和12月)。
|
|
表 4 不同坡度、坡向年均太阳潜在总辐射统计表(单位:MJ·m-2·d-1) |

|
图 4 不同坡度下阴坡、阳坡潜在太阳辐射均值变化曲线 |
从图表变化可以看出:就全年而言,阴坡的潜在太阳总辐射随坡度的增加而逐渐减小,而阳坡潜在太阳总辐射则随坡度的增大呈现先增后减的变化趋势。平均而言,阳坡的太阳辐射量可达阴坡的1.7倍左右,无论阴坡还是阳坡的太阳潜在总辐射的标准差均随坡度增加表现出递增的趋势;在高太阳高度角的6月,随着坡度的增大,阴坡阳坡间的潜在太阳辐射均逐渐较小,但两者间的差值变化不大,说明夏季阴坡、阳坡的潜在太阳总辐射空间差异不明显;随着太阳高度角的增大,地形因子对太阳辐射的影响渐趋增大,阴坡、阳坡太阳潜在总辐射差距在冬季的12月表现显著,阳坡太阳潜在总辐射量可达阴坡的4倍左右。
由图 4中还可看出,不同坡度下阴坡、阳坡太阳直接辐射变化同太阳总辐射特征一致,不再赘述;对天空散射辐射而言,阳坡天空散射辐射均大于阴坡,除12月阳坡天空散射辐射随坡度增加表现出先增后减的趋势外,其余均随坡度增加呈减小趋势,其中6月阳坡天空散射辐射随坡度减小趋势较大;地表反射辐射则是阴坡大于阳坡,除6月份阳坡地表反射辐射随坡度增加先增后减外,其余均随坡度增加呈减小趋势,其中年均和6月的阴坡地表反射辐射减小趋势较大。
4 结论(1) 本文利用太阳辐射计算模型,针对地形差异条件下太阳总辐射的再分配特点以及DEM数据分辨率对计算结果的影响,在充分考虑地形和大气衰减的情况下,综合运用GIS,建立了一个90m地形分辨率的山西高原太阳潜在总辐射空间分布模型。
(2) 通过利用研究区域内日辐射观测资料,选取同期总低云量为零作为晴空天气条件的观测值对模型进行检验分析,结果表明该模型适合山西高原的潜在太阳总辐射计算分析。
(3) 从空间分布上看,区域年太阳潜在总辐射值由北到南逐渐增高,但是纬向分布特点并不明显。太阳年辐射总量基本上是山区平川间的辐射差异远大于纬向间分布差异,表现出明显的非地带性分布特征。就时间分布上看,区域潜在太阳辐射有明显的月际变化,各月中6月的太阳潜在辐射量最大,12月最小;按照季节划分,太阳潜在辐射量的大小依次为夏季>春季>秋季>冬季,表现出太阳潜在辐射的季节分布不对称性。
(4) 地形因子对潜在太阳总辐射的影响在不同的太阳高度角下表现不一,在太阳高度角较高的冬季12月,地形因子对太阳辐射的影响较大,阳坡辐射量可达阴坡的4倍左右;而在夏季的6月份,两者的辐射量差距很小;从整个年度来看,阴坡阳坡的太阳辐射量差距可达1.7倍左右。太阳直接辐射占总辐射的94%,天空散射和地表反射辐射各占约2%和4%,阳坡天空散射辐射均大于阴坡,地表反射辐射则是阴坡大于阳坡,且基本上随坡度增加呈减小趋势。
(5) 虽然该模型总体上能够用于区域潜在太阳辐射计算分析,但由于模型自身以及区域大气的原因,模型存在一定程度的计算误差,而且误差表现出一致的变化趋势,这与山西高原的气候特征以及环境空气污染的状况是一致的。今后的研究中应重点根据区域的气候及大气状况进行必要的修正。
傅抱璞, 1958. 坡地对日照和太阳辐射的影响[J]. 南京大学学报(自然科学), 2: 23-46. |
傅抱璞, 1964. 起伏地形中辐射平衡各分量的计算[J]. 气象学报, 34(1): 62-73. DOI:10.11676/qxxb1964.007 |
傅抱璞, 1983. 山地气候[M]. 北京: 科学出版社.
|
傅抱璞, 虞静明, 卢其尧, 1996. 山地气候资源与开发利用[M]. 南京: 南京大学出版社.
|
张雪芬, 陈东, 付祥健, 等, 1999. 河南省近40年太阳辐射变化规律及其成因探讨[J]. 气象, 25(3): 21-25. DOI:10.7519/j.issn.1000-0526.1999.03.005 |
李占清, 翁笃鸣, 1988. 丘陵山地总辐射的计算模式[J]. 气象学报, 11, 46(4): 461-468. DOI:10.11676/qxxb1988.058 |
朱志辉, 1989. 坡度辐射场研究及其地理学应用[J]. 地理研究, 8(2): 91-100. |
林正云, 1994. 福建省散射辐射的计算方法及其分布特征[J]. 气象, 20(4): 10-14. DOI:10.7519/j.issn.1000-0526.1994.04.002 |
Dozier J, Outcalt S I, 1979. A approach toward epnergy balance simulation over rugged terrain[J]. Geographic Anal, 11: 65-85. |
Dozier J, Frew J, 1990. Rapid calculation of terrain parameters for radiation modeling from digital elevation data[J]. IEEE Transaction on Geoscience and Remote Sensing, 28(5): 963-969. DOI:10.1109/36.58986 |
Conese C, Gilabert M A, Maselli F, 1990. Topographic normalization of TM scenes through the use of an atmospheric correction method and digital terrain models[J]. Photogrammetric Engineering and Remote Sensing, 28(5): 963-969. |
Civco D L, 1993. Topographic normalization of landsat the matic mapper digital imagery[J]. Photogrammatric Engineering and Remote Sensing, 59(12): 1745-1753. |
李新, 程国栋, 陈贤章, 等, 1999. 任意条件下太阳辐射模型的改进[J]. 科学通报, 44(9): 993-998. |
李新, 陈贤章, 曾群柱, 1996. 利用数字地形模型计算复杂地形下的短波辐射平衡[J]. 冰川冻土, 18(3): 344-353. |
曾燕, 邱新法, 刘昌明, 等, 2003. 基于DEM的黄河流域天文辐射空间分布[J]. 地理学报, 58(6): 810-816. DOI:10.11821/xb200306002 |
曾燕, 邱新法, 刘昌明, 等, 2005. 起伏地形下黄河流域太阳直接辐射分布式模拟[J]. 地理学报, 60(4): 680-688. DOI:10.11821/xb200504017 |
杨昕, 汤国安, 王雷, 2004. 基于DEM的山地总辐射模型及实现[J]. 地理与地理信息科学, 20(5): 41-44. |
何洪林, 于贵瑞, 牛栋, 2003. 复杂地形条件下的太阳资源辐射计算方法[J]. 资源科学, 25(1): 78-85. |
杨昕, 汤国安, 肖晨超, 2007. 太阳辐射模拟的DEM尺度影响因素分析[J]. 地球信息科学, 9(2): 14-19. |
Kreith, F., and Kreider, J. F. 1978. Principles of Solar Engineering. McGraw-Hill, New York, NY.
|
Kumar L, Skidmore A.K., Knowles E, 1997. Modelling topographic variation in solar radiation in a GIS environment[J]. International Journal for Geographical Information Science, 11(5): 475-497. DOI:10.1080/136588197242266 |
Gates, D. M. Biophysical Ecology (New York: Springer-Verlag), 1980.
|
张宇, 赵四强, 1991. 关于逐日太阳辐射估算方法的探讨[J]. 气象, 17(10): 52-54. DOI:10.7519/j.issn.1000-0526.1991.10.014 |
 2009, Vol. 35
2009, Vol. 35