2. 中国科学院大气物理研究所
2. Institute of Atmospheric Physics, Chinese Academy of Sciences
暴雨是我国的主要灾害,而引起暴雨的天气形势是有区别的,由台风(包括热带风暴、强热带风暴、台风、强台风和超强台风)引发的暴雨是这些形势当中的重要一员,最大暴雨过程往往是由台风引起。历史上著名的75·8特大暴雨过程就是一个典型的例子,它与7503号台风的活动密切相关。平均每年有7个台风在我国登陆, 登陆频数呈现显著的年际变化特征。最多年有12个,最少年有3个。在夏秋季节,台风是东南沿海最重要的灾害性天气系统。
迄今为止,沿海地区的预报员和从事台风研究的科研人员对西太平洋台风活动和其预报积累了大量知识和经验[1],国内外对各种台风暴雨及其预测这一科学问题也进行了不少的研究[2-16]。Bosart等对Agnes飓风产生的强降水特征进行研究[2],发现对流层中高层弱的短波扰动触发了本次降雨的持续增长。与Eloise飓风进行对比后发现,虽然两次过程的雨区分布极为相似,但它们物理机制是明显不同的。Atallah等利用位涡距平研究了Floyd飓风的降水分布特征[3]。降水主要与飓风和深厚中纬度槽共同作用而产生的强对流层斜压区有关。Thorncroft等对Felix和Iris飓风进行对比研究[4]。两个飓风都途经西北欧地区,但只有Iris发展成为高纬度风暴系统。研究发现,垂直切变对该飓风结构的演变贡献巨大。Iris之所以发展,是因为受外界强切变环境场影响,受大尺度斜压气旋影响,以及受有利于暖心结构维持的因素影响。大尺度斜压波动的发展和飓风在移动过程中结构的演化是此类事件预测的考虑重点。Caracena等研究了Amelia飓风导致暴雨山洪的原因[5]。认为是飓风系统与雷暴复合体相互作用的结果。有5个方面的特征:一条向东发展的纬向气流边界线位于风暴南侧;狭长高湿度水汽边界层气团迅速从西南向风暴区移来;有当地山区抬升的暖而干的气团配合;对流层中层短波扰动的作用;当地加热所产生的热力对流云团。杨克明等[6]分析了2001年我国台风暴雨的天气气候特征及造成暴雨过程的物理因子,为实时预报业务提供了参考。牛健等[7]利用Q矢量散度场分析了2004年的几次重要台风暴雨过程,认为低层等压面上Q散度场的演变对台风暴雨预报有重要贡献。赵思雄等[8]对“75·8”特大暴雨进行了数值预报试验研究,指出在模式中尽量使用实测风资料作为初始资料,证明了本次暴雨发生的过程与风场关系较大。孙建华等[9]对9406(Tim)台风登陆北上引发我国东部大暴雨的过程进行了诊断。指出此次台风暴雨过程在低层除平流项外, 散度项也比垂直输送项和扭转项大一个量级。而高空散度项、垂直输送项和扭转项同量级, 此时扭转项的贡献也不可忽视。边清河等[10]通过对52年以来的台风暴雨个例研究,统计了华北地区台风暴雨的气候特征。孙建华等[11]指出“96.8”暴雨过程中入侵的弱冷空气是由华北高压南侧的偏东风引导至台风倒槽外围, 是属于比较少见的登陆台风北上受高压阻挡停滞类型; 台风倒槽内发生发展的2个中尺度对流云团是造成此次暴雨的直接影响系统。此外,太行山对对流系统的阻挡可能是导致强降水长时间维持在石家庄的原因之一。李江南等[12]利用模式对登陆台风Fitow (2001)的暴雨中心位置和雨量进行了比较成功的预报。该工作对于扩展更多台风暴雨个例的预报提供了珍贵的参考。王淑静等[15]总结了预报台风暴雨落区的业务化实用判据,指出在台风倒槽的顶部, 是台风与西风带系统相互作用最活跃的地方, 易产生次天气尺度及中尺度扰动,往往是突发性暴雨的生成之地。田辉等[16]研究了华南、华东沿海登陆台风暴雨和大风特征。
大气科学发展到今天,逐渐形成了相对成熟的包括台风暴雨预报在内的关于各类天气现象的众多预报方法技术[17-20]。一般情况下,这些方法可以得到基本的结论,但预报准确率不是足够理想,空报率和漏报率不能达到很好的一致。
台风暴雨机理及各种预报技术的研究对成功预防灾害起到了指导作用,然而目前国内外关于台风暴雨业务预报技术方面的研究开展得不多,表现在台风暴雨降水预报的准确性有待进一步提高。台风暴雨预报领域的不足体现在两个方面:在理论研究上,对台风暴雨降水预报的准确率徘徊不前,在技术上,对台风引发暴雨过程的落点落区预报中有“非漏即空”和“不一致”现象:漏报率低了,空报率就高;空报率减少,漏报率又增加。要从根本上改变这些,就要以创新的思维,从不同角度(甚至前人很少涉及的领域)展开研究。基于此,文章从预报技术方面,用统计和相似的方法,通过大量细致的试验,试图在台风暴雨预报中探索出一种好的方法,建立一种好的预报模型,填补台风暴雨预报领域的空缺与不足,更全面提高台风暴雨的预报水平(不只是准确率,还包括空报率、漏报率的一致性要好)。
文献[36]介绍了SMAT技术的详细情况,在此基础上,文章进一步介绍该技术在台风暴雨预报试验中的具体应用、试验的详细过程以及所得到的结果:预报区域内台风暴雨预报模型(MAT-Typhoon)。文章的工作可以进一步证明SAMT技术的可行性和应用价值。
1 资料、技术方法和试验的准备 1.1 资料的准备论文所使用的资料包括:逐日探空资料、常规天气图资料、地面观测资料以及中尺度模式的运转结果。在处理探空资料中用到了重要的插值技术,在1.3节中将介绍该技术,探空资料经过处理[21-22]后被用来做相似试验。天气图资料和地面观测资料被用来分析研究区域内台风暴雨的季节分布特征以及有无暴雨产生的个例数目统计,为文章的相似试验提供基础。一些研究人员对数值产品进行释用,然后将其用在预报技术业务中[24]。参考他们的做法,文章在第三级预报中将模式积分若干小时后的资料作为相似因子,进行动态过程的相似描述。文章使用MM5模式[23]为第三级相似试验提供相似因子。资料在研究中的分配是这样的,选用1990—1999年资料进行试验,建立、调试预报模型。选用2000—2002年资料进行试报。
1.2 预报区域和台风型暴雨天气的确定预报区域选在浙江省的东南沿海区域(简称“浙东南”,25°~31°N、118°~124°E,图 1),台风型天气的分型标准为,台风中心位于20°~30°N,128°E以西附近,且未来有向西移动的趋势。
|
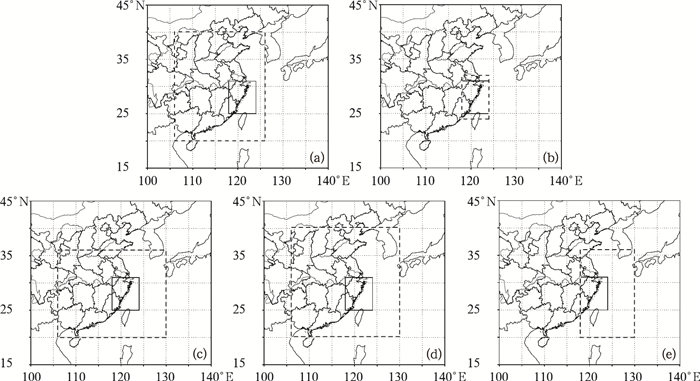
图 1 前两级试验的备选相似区域 实方框代表预报区域,虚方框代表备选的相似区 |
对于任意物理量φ进行如下假设[25-26]:α,β分别代表站点类型和资料类型,它们的组合可以包括:测站上的观测值(α=i, β=o),网格点上的初估值(α=k, β=g),格点初估值被插值到站点上(α=i, β=j),格点上的分析值(α=k, β=a)等。φa为真值,e为各种误差,即
| $ \varphi _{^a}^\beta = {\varphi _a} + e_a^\beta $ | (1) |
假设p为权重因子。一般,格点分析值包括格点初估值与订正值两部分,即
| $ \varphi _{^k}^\beta = \varphi _k^g + \sum\limits_{i = 1}^n {{p_i}\left( {\varphi _i^o - \varphi _i^g} \right)} $ | (2) |
通过以上各式可得
| $ e_k^a = e_k^g + \sum\limits_{i = 1}^n {{p_i}{\varphi _i}'} $ | (3) |
此处,ekα为网格点上的分析误差,ekg为格点上的初估误差值,φi′为测站观测值φio与初估值φig之差。接下来,只要合理选取权重,使得格点分析误差(或均方根误差)达到最小,则,可以得到最优分析场。为了求解方便,不妨将此问题转化为求取E′极小值的问题。
| $ E' = 1 - 2\sum\limits_{i = 1}^n {{p_i}{\rho _{ki}}} + \sum\limits_{i = 1}^n {\sum\limits_{j = i}^n {{p_i}{p_j}{\rho _{ki}}} } + \sum\limits_{i = 1}^n {p_i^2{\eta _i}} $ | (4) |
E′为分析值的相对均方误差,ρ, η分别为与要素统计结构(测站、格点以及它们之间相对位置情况)和测站观测精度相关的量。而E′取最小值的条件为:
| $ \frac{{\partial E'}}{{\partial {p_i}}}{\rm{ = }}0 $ | (5) |
此时,由式(5)求解最佳权重,由式(2)确定格点分析值。
1.4 综合多级相似技术(SMAT)和暴雨预报评分技术该技术包含了三级相似过程,先完成前两级试验,得出初步结果,然后通过第三级试验,引入数值模式产品对前两级试验进行修订,得出最终结果。每一级试验中,根据空报率大小,分别选取最佳相似因子组合、最佳相似区域(即,关键区)和最佳相似样本(即,标准样本),并得出本级的相似参数。除了第三级的修订外,在前两级试验内部,还要进行调试和修订[36]。文章采用的评估模型预报性能的指标包括:临界预报成功指数(CSI)、预报正确率(COR)、空报率或伪警率(FAR)、漏报率或击中率(POD),关于这些指标的介绍可参考文献[27-35]。
2 相似预报试验过程 2.1 前两级的试验过程及性能调试根据1.1节中的统计分析,在10年试验样本库中,选用27个台风型有暴雨个例,40个台风型无暴雨个例,共计67个个例进行研究。在3年独立样本库中,选用8次台风型暴雨过程,17次台风型无暴雨个例过程,共25个样本进行试报检验。
2.1.1 试验准备第一级相似的因子组合共有58种(表略)。记角标3表示850hPa层的物理量(t3,td3,h3),角标4表示700hPa层的物理量(t4,td4,h4), 其中,t为温度,td为露点温度,h为位势高度。在第二级相似中,记K指数为K,850hPa层(代表边界层顶)的上升运动为W,水汽通量散度(850hPa、700hPa两层的平均值)为S,850hPa层的温度平流为P,24小时变温(850hPa层)为TT,垂直螺旋度为C(850hPa层到500hPa层间,代表高空深度层特性),总共6种参与筛选的因子组合:第一种,K, S, W, C, TT;第二种,K, S, W, C, P;第三种,K, S, W;第四种,K, S, W, TT;第五种,K, S, W, P;第六种,K, S, W, C。图 1给出了前两级相似区域备选方案的地理位置,总共有5种,经纬度范围(区域方案序列号依次按顺序排列分别是:106°~126°E、20°~40°N(图 1a);118°~124°E、24°~32°N(图 1b);106°~130°E、20°~36°N(图 1c);106°~130°E、20°~40°N(图 1d);118°~130°E、20°~36°N(图 1e)。
2.1.2 试验过程(1) 第一级相似:综合形势场的相似
首先计算因子组合,区域组合,相似样本等项目的空报率,将各参加筛选项目的空报率按其序列号绘制成图 2。从图 2中可以分析,空报率受样本的影响最大,受因子和区域前两级试验的备选相似区域实方框代表预报区域,虚方框代表备选的相似区的影响相对要小,表明描述相似时参照物的选取十分关键。根据图 2的结果,依次选取空报率最小的项目作为本级的各个参数。选取第36种因子组合(850hPa层的高度场、700hPa层的温度场和露点场),空报率为85%;选取第一种区域方案,空报率为85%;从27个标准样本中选取第22个暴雨样本(1996年8月1日)为标准样本,空报率68%;同时选取与其对应的CT(0.0335,临界相似离度,相似离度的最大值)为本级相似的最终临界值。本级试验所得到的相似参数罗列于表 2中。

|
图 2 空报率分布 |
|
|
表 2 三级相似参数列表 |
(2) 第二级相似:局地小气候特征的相似
类似于第一级相似,根据各参选项目空报率图(略),依次对最佳因子组合、关键区、最佳相似样本进行选取,得出本级相似参数。通过试验挑选出的最佳因子组合为第二种。根据确定了因子组合后各相似区域下的空报率看,选第四种区域作为关键区。从27个暴雨样本在所选定的因子组合、关键区下的空报率看,选第四个暴雨样本(1990年8月20日)为标准样本,空报率是95%,同时选取与其对应的CT(0.0257)为本级相似最终临界值。
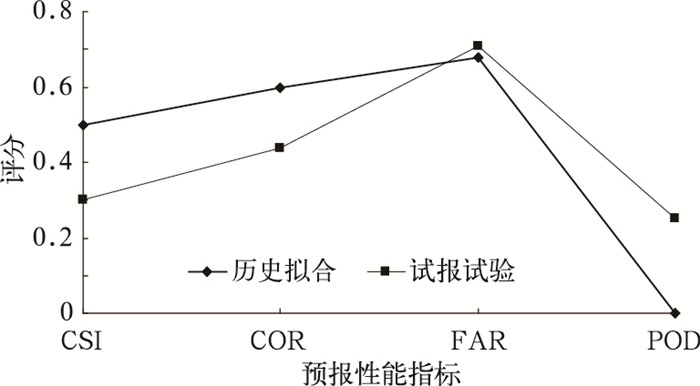
2.1.3 试验的调试修订及模型性能检验从图 3可以看出,在刚完成两级预报试验之初,各项性能指标在历史拟合(回报)时都比较理想,CSI为0.5,COR为0.6,POD为0;然而试报的结果中性能指标呈普遍下降趋势,CSI为0.3,COR为0.44,FAR也有所增加,且出现了漏报现象。有必要进行参数调试和修订。表 1给出了三种调试方案。
|
图 3 历史拟合与试报试验的指标分析 |
|
|
表 1 调试方案设置 |
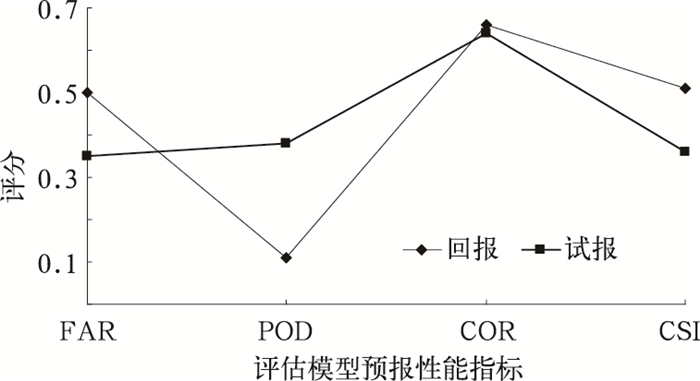
方案1调试后作用不大,各项指标性能没有明显改进。方案2中,考虑到不同型暴雨的物理因子条件场(局地小气候性、地域性)的相似有较大区别性(如,台风型暴雨和气旋型暴雨的关键区是不同的),针对二级相似调整其物理因子、相似区域。将二级相似区域方案适当缩小,考虑到台风出现在预报区的偏东偏南侧,因此关键区的预设应位于预报区的偏东偏南方位,将各经纬度范围(图略)调整为:118°~133°E,20°~36°N;120°~128°E,25°~33°N;120°~125°E,25°~33°N。在二级相似原有的因子基础之上,考虑到台风属于深厚系统,新引入一批因子,并调整原有的个别因子,重新将它们组合成新的因子方案。具体如下:新引入的因子,最大可降水率Ⅲ(1000hPa层到200hPa层),对流不稳定度SITA(850hPa层到700hPa层),湿位涡MPV(850hPa层到250hPa层);调整后的因子,垂直螺旋度C从原来的中低层(850hPa层到500hPa层间)扩展到整个空间层(850hPa层到200hPa层);未变的因子,边界层顶(850hPa层)的上升运动W,850hPa层的温度平流P,24小时变温(850hPa层)TT。新组合后的因子方案包括:第一种,SITA,Ⅲ,C,W,TT;第二种,SITA,Ⅲ,C,W,P;第三种,SITA,Ⅲ,C,W,MPV,TT;第四种,SITA,Ⅲ,C,W,MPV,P。根据相似因子组合、相似区域和标准样本的空报率情况(空报率图略),所选因子方案为1,区域方案为1,第14个暴雨个例(1992年9月22日)作为标准样本,CT值为0.0196。以上是修正后的第二级相似参数情况。经过方案2的调试,回报CSI达到了0.54,其他性能指标也有较大提升(略去历史拟合与试报试验的指标分析)。在模型自测时,这算是一次比较成功的修订。不足之处在于,试报的CSI偏低,需要利用方案3进一步修正。此外,从修订过程来看,在做相似试验(包括第三级)时,物理因子的选择非常重要,而相对来讲试验效果受相似区域选择的影响不大(这里略去相似因子和相似区域在空报率方面对试验效果影响的详细对比)。方案3中,在调试二级相似的CT值的过程中,发现将CT值降为0.0187后的回报、试报结果比较理想,CSI维持在0.50以上,试报结果,CSI比方案2时提高了7个百分点(如图 4)。
|
图 4 前两级预报调好的历史拟合与试报试验的指标分析 |
根据1.1节中的统计分析,从试验样本库中,选用17个台风型有暴雨个例和14个无暴雨个例,共计31个个例进行相似预报试验。从独立样本库中,选用8次台风型暴雨过程,17次台风型无暴雨个例过程,共计25个样本做试报试验。本级的相似区域方案经纬度(图略):118°~130°E, 20°~36°N; 120°~128°E, 25°~33°N; 120°~125°E, 25°~33°N。预先给出一批经验因子,这些因子通过模式积分若干小时获得,这里的若干小时是以3小时为间隔单元的3n(n取自然数)时间步长的物理相似因子。利用极值剔除法和减空法依次筛选因子。经筛选后得到如下因子组合:CFQ为模式积分6小时1000~500hPa层之间的垂直风切变,ADVQ为模式积分12小时500hPa层的湿度平流,VORT为模式积分6小时850hPa层的涡度。本级其他相似参数:关键区为第二个相似区域,标准个例为1994年8月21日, CT值为0.0208。
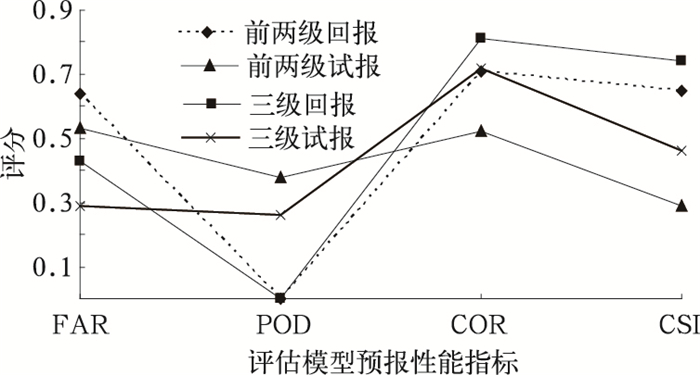
图 5为加入第三级预报前后的回报、试报结果。可以看出,引入第三级预报后,回报FAR由64%修订为43%,试报空报率减少了23个百分点,说明以数值产品为资料的第三级预报具有减少空报率的作用。同时,试报CSI从二级预报的0.29提高到了0.46,漏报率减少了12个百分点,准确率提升了20个百分点,说明第三级预报对前两级预报起到了很好的修订作用。引入第三级相似,利用数值产品作修订预报,在解决了因“宁空勿漏”思想导致的空报率偏高问题的同时,也减少了漏报率,其他指数也比两级预报时更好。表 2总结了各级的相似参数情况,这也是作者所建立的预报模型中的参数情况。
|
图 5 两级预报和三级预报的效果对比 |
文章研究区域东濒东海,南界福建,地势自西南向东北呈阶梯状倾斜,群山盘结,平原、盆地交错,水系复杂。特征如此明显的区域其发生台风型暴雨的机理何在,跟其他地域类似过程相比较,其业务预报中有何自身特点?李博等曾指出[13],由MPV的负值分布引起的条件性对称不稳定是台风发生发展的重要机制。而第三级试验结果表明,对于台风系统产生暴雨天气有利的物理因子场中不包括MPV,原因何在?一方面这可能是由于预报区域位于台风外围而非眼壁区的缘故;另一方面,这可能由于在具体个例中,对台风发生发展起重要作用的因子会根据不同的地区而有所变化。各类天气系统具有统一属性,但受地形、地貌等因素影响又很大。从表 2中总结的本试验各级最佳相似因子分析,要想准确把握本地区台风暴雨的预报,至少以下几方面需要考虑:降水产生前,700hPa层的水汽、温度条件和850hPa层的降水系统的配合能否提供有利的综合形势场?当地能量的积聚、降水条件的积聚以及冷空气的积聚和持续的上升运动能否给予降水较好的初始触发?降水产生后,空间垂直风、高空湿度平流水汽的输送情况以及低空涡度配合的变化能否确保持续台风暴雨动力过程的维持?这些物理意义所对应的物理量就是表 2中给出的各因子,在业务预报中这些因子应该重点给予考虑。
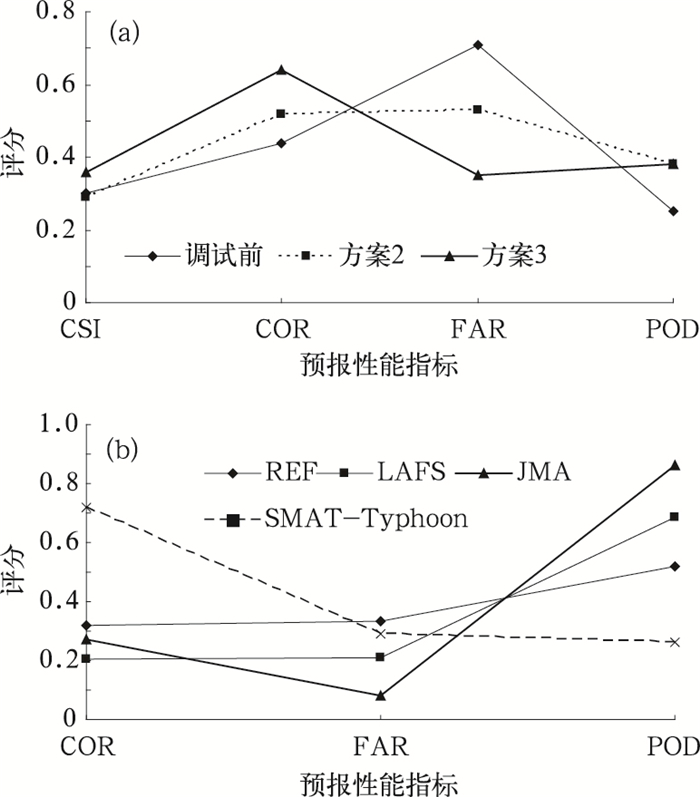
3.2 相似试验的再分析在分析图 3时指出修正、调试很有必要,经过两种调试过程(图 6a,调试细节参见2.1节)后,CSI从0.3增加到0.36,COR从0.44增加到0.64,FAR从0.71下降到0.35,尽管POD有所上升,但平均而言,对预报的修正还是可取的。其中,方案3调试效果最好,它是在方案2基础上,对CT值进行了再次调试。方案2和方案3都主要是针对第二级相似的各参数进行了调试(这样做的根据在2.1节有说明)。对比第二级相似调试前和调试后的关键区(分别为:106°~130°E;20°~40°N(图 1d)和118°~133°E;20°~36°N), 发现将描述第二级相似的区域集中在预报区域偏东偏南方位比较好。从调试前后相似因子的变化和比较中发现,台风属于存在于整层空间的深厚非完全对称性的涡旋系统,对于一些物理量应考虑到从整层去描述其相似(如,垂直螺旋度C从中低层变化为整层);而边界层内的上升运动在调试后仍然是重要因子,这可能是由于风场的低层触发作用对于台风的产生和维持比较重要。CSI是衡量暴雨业务预报的重要指标。目前,暴雨业务预报的平均CSI是0.35左右,对于大暴雨和特大暴雨甚至还要低些。在本试验中,建模时的CSI高于0.7,且漏报率为0。在试报阶段,CSI也能保持在0.45以上。从图 6b(REF代表预报员预报,LAFS代表中国数值预报,JMA代表日本数值预报,SMAT-Typhoon代表台风暴雨预报模型)可知,通过对比各种预报方法的效果,发现SMAT-Typhoon的优势在于准确率(0.72)和漏报率(0.26)比较好,而空报率则介于中游偏差的位置,但总体来讲还是不错的。
|
图 6 前两级预报的修正、调试效果(a)和各种预报方法结果(b) |
文章选用67个个例进行试验,建立起了两级预报模型,用25次个例进行试报。选用31个个例进行试验,建立起了第三级订正模型,用25次个例进行试报。通过文章工作,得到以下结论:
(1) 得出了研究区域台风暴雨预报模型(SMAT-Typhoon),试验和检验工作初步说明该模型满足各种预报性能指标相一致的要求,达到了引言部分所提到的期望,进一步说明SMAT技术有较强的平均预报能力。
(2) 模型SMAT-Typhoon的回报CSI高于0.7,且漏报率为0;试报CSI也能保持在0.45以上;其准确率(0.72)和漏报率(0.26)也比较理想;只是空报率(0.29)没有体现出明显的优势,这与本技术中所包含的“宁空勿漏”思想有关[36]。
(3) 从模型建立过程中试验和修订效果分析,在描述样本之间相似程度时,物理因子的选择非常重要,而相对来讲相似试验效果受相似区域选择的影响不大,这给今后类似的研究工作提供了一个参考:在初步考虑各种因素的前提下,研究重点应放在对物理因子的选取和分析上。而关键区的选择技巧在于与所对应的天气型所处的位置要联系起来(如,台风型暴雨的关键区一般应在预报区的偏东偏南方向,而如果系统在预报区的西北方向,则关键区应集中考虑在对应的区域)。此外,选取相似因子时,也要结合产生暴雨的主要系统进行考虑;文章还给出了当地业务预报过程中应该着重考虑的一些物理量,对于实际预报具有一定的指导作用。
致谢:文章得到解放军理工大学陆汉城教授、原空军气象学院副院长杨国祥教授的指导,两名审稿老师对本文提供了重要帮助,在此一并致谢。
陶诗言, 1988. 评《台风预报手册》[J]. 气象科学研究院院刊, 3(2): 223-224. |
Bosart L F, Carr F H, 1978. A case study of excessive rainfall centered around wellsville, New York, 20-21 June 1972[J]. Monthly Weather Review, 106: 348-362. DOI:10.1175/1520-0493(1978)106<0348:ACSOER>2.0.CO;2 |
Atallah E H, Bosart L F, 2003. The extratropical transition and precipitation distribution of Hurricane Floyd(1999)[J]. Monthly Weather Review, 131: 1063-1081. DOI:10.1175/1520-0493(2003)131<1063:TETAPD>2.0.CO;2 |
Thorncroft C, Jones S C, 2000. The extratropical transitions of Hurricanes Felix and Iris in 1995[J]. Monthly Weather Review, 128: 947-972. DOI:10.1175/1520-0493(2000)128<0947:TETOHF>2.0.CO;2 |
Caracena F, Fritsch J M, 1983. Focusing mechanisms in the Texas Hill Country flash floods of 1978[J]. Monthly Weather Review, 111: 2319-2332. DOI:10.1175/1520-0493(1983)111<2319:FMITTH>2.0.CO;2 |
杨克明, 王文东, 张守峰, 等, 2002. 2001年台风暴雨的分析[J]. 气象, 28(10): 22-27. |
牛键, 沈晓玲, 2006. 2004年几次台风暴雨Q矢量诊断的比较分析[J]. 灾害学, 21(2): 90-94. |
赵思雄, 周晓平, 1984. 风场在预报暴雨发生中的作用———1975年8月特大暴雨的数值实验[J]. 大气科学, 8: 1-61. DOI:10.3878/j.issn.1006-9895.1984.01.01 |
孙建华, 赵思雄, 2000. 登陆台风引发的暴雨过程之诊断研究[J]. 大气科学, 24(2): 223-236. |
边清河, 丁治英, 吴明月, 等, 2005. 华北地区台风暴雨的统计特征分析[J]. 气象, 31(3): 61-65. DOI:10.7519/j.issn.1000-0526.2005.03.014 |
孙建华, 齐琳琳, 赵思雄, 2006. "9608"号台风登陆北上引发北方特大暴雨的中尺度对流系统研究[J]. 气象学报, 64(1): 57-71. |
李江南, 王安宇, 侯尔滨, 等, 2004. 台风Fitow降雨的数值预报试验[J]. 热带海洋学报, 23(1): 16-24. |
李博, 陆汉城, 裴蕾, 2003. Andrew飓风发展过程中的湿位涡诊断[J]. 解放军理工大学学报(自然科学版), 4(6): 84-89. |
齐琳琳, 赵思雄, 2004. 一次热带低压引发上海特大暴雨过程的中尺度分析[J]. 大气科学, 28(2): 254-268. |
王淑静, 周黎明, 陈高峰, 1997. 解释台风暴雨落区判据的探讨[J]. 应用气象学报, 8(2): 167-174. |
田辉, 马开玉, 林振山, 1999. 华南、华东沿海登陆台风暴雨和大风的分析[J]. 应用气象学报, 10(增刊): 148-152. |
徐夏囡, 李泽椿, 1996. 国家气象中心台风、暴雨预报服务系统的设计和研究[J]. 应用气象学报, 7(4): 406-413. |
邵明轩, 刘还珠, 窦以文, 2006. 用非参数估计技术预报风的研究[J]. 应用气象学报, 17(增刊): 125-129. |
王莉, 黄嘉佑, 1999. Kalman滤波的试验应用研究[J]. 应用气象学报, 10(3): 276-283. |
盛春岩, 浦一芬, 高守亭, 2006. 多普勒天气雷达资料对中尺度模式短时预报的影响[J]. 大气科学, 30(1): 93-106. |
刘小宁, 鞠晓慧, 范邵华, 2006. 空间回归检验方法在气象资料质量检验中的应用[J]. 应用气象学报, 17(1): 37-44. |
任宏利, 丑纪范, 2005. 统计-动力相结合的相似误差订正法[J]. 气象学报, 63(6): 988-994. DOI:10.11676/qxxb2005.094 |
Anthes R A, Warner T T, 1987. Development of hydrodynamics models suitable for air polloution and mesomeleorological studies[J]. Monthly Weather Review, 106: 1045-1078. |
张立祥, 陈立强, 刘文明, 等, 2000. 东北区夏季月降水数值产品释用预报方法[J]. 应用气象学报, 11(3): 348-355. |
王跃山, 2001. 客观分析和四维同化(Ⅱ)客观分析的主要方法[J]. 气象科技, 29(1): 1-9. |
李建通, 杨维生, 郭林, 等, 2000. 提高最优插值法测量区域降水量精度的探讨[J]. 大气科学, 24(2): 263-270. |
Donaldson R J J, Dyer R M, and Kraus M J. An objective evaluator of techniques for predicting severe weather events[R].Preprints, Ninth Conf.on Severe Local Storms, Norman, Oklahoma, Amer.Meteor.Soc., 1975:321-326.
|
Stanski H R, Wilson L J, Burrows W R, 1991. Survey of common verification methods in meteorology[J]. World Weather Watch Technical Report, 8: 89-96. |
许美玲, 孙绩华, 2002. MM5中尺度非静力模式对云南省降水预报检验[J]. 气象, 28(12): 24-27. |
张建海, 诸晓明, 2006. 数值预报产品和客观预报方法预报能力检验[J]. 气象, 32(2): 58-63. DOI:10.7519/j.issn.1000-0526.2006.02.011 |
晁淑懿, 金荣花, 1996. 一种综合相似中期预报模型[J]. 应用气象学报, 7(3): 300-307. |
王雨, 2003. 2002年主汛期国家气象中心主客观降水预报对比检验[J]. 气象, 29(5): 21-25. DOI:10.7519/j.issn.1000-0526.2003.05.005 |
Shao Mingxuan, Wu Qinli, 2004. An objective forecast experiment in precipitation at stations[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 140(1): 46-55. |
Carr F H, Bosart L F, 1978. A diagnostic evaluation of rainfall predictability for tropical storm Agnes, June 1972[J]. Monthly Weather Review, 106: 363-374. DOI:10.1175/1520-0493(1978)106<0363:ADEORP>2.0.CO;2 |
施能, 魏凤英, 封国林, 等, 1997. 气象场相关分析及合成分析中的梦特卡洛检验[J]. 南京气象学院学报, 20(3): 355-359. |
李博, 赵思雄, 陆汉城, 等, 2008. 综合多级相似预报技术在暴雨短期预报中的检验[J]. 应用气象学报, 19(3): 307-315. DOI:10.11898/1001-7313.20080306 |
 2009, Vol. 35
2009, Vol. 35