引言

目前，超级集合预报技术的研究与应用在国内外气象领域已经相当广泛^[1-5]。所谓超级集合包括不同初始场、不同模式和不同的物理过程的集合，集成产品包含了更多的信息，这无疑会提高数值预报的参考价值。但因为集合预报巨大的计算量，需要大型计算条件作后盾。另外，集合是把所有成员聚集在一起的状况，仍保持了每个成员的个性，提供的是一种概率性的预报，但现实的业务预报却要求提供唯一性的预报，这就需要将所有成员提供的信息综合处理成一个统一的结果，从个性之中提取各成员的共性，也就是集成预报。对于省级及其以下气象台站而言，发展基于集合预报思想的集成预报技术既是业务所需，也是一种比较经济、有效的途径。

目前国内外的集成预报都有开展，但总的说来这些集成预报方法中的成员在集成预报中的权重主要依赖于历史样本统计得出，也就是说权重是静态的、固定的，用一个固定的指标解决复杂的问题，就势必影响预报效果；通常的集成预报技术一般不考虑各成员预报能力在不同季节、不同地域和不同预报时效的不同表现，对某一成员采取统一的权重系数，这有可能导致集成预报性能的不稳定；大多数集成预报成员的权重是建立在长序列的历史样本基础上的，新的成员如不具备足够的历史样本，将无法纳入集成预报；国内外有很多集成方法是针对单一预报对象(如降水、温度、热带气旋路径等^[6-7])进行的，多用于短期气候预测^[8-11]，而系统全面地包括不同层次形势场、物理量的短期预报集成方法及相关的集成统计产品如集成矩、集成簇等则较为少见。

基于上述问题，本文提出了一种基于超级集合思想的多模式动态变权集成预报方法，可摆脱对大量历史样本的依赖性，对成员的增减或是成员预报能力的变化也能够作出适时的响应，每个成员在集成预报中的权重系数能自适应地动态调整，动态反映每一成员在不同季节、不同时效、不同区域的预报水平。

1 变权集成预报方法的引入

目前解决初值条件误差和模式误差的途径是使用集合天气预报系统(EPS)，以此估计各种预报结果的发生概率。EPS是由略微不同的初值或不同模式作出个别预报(预报成员)的集合，集合平均代表EPS确定性的预报结果，各成员对集合平均的离散度或标准差代表EPS的不确定性，一般认为由内部变率造成。任一地点和任一变量的EPS不确定性可由概率密度函数(PDF)表征，它是由不同集合成员构成的一种频率分布。集合预报可看作是计算条件概率分布的一种过程，即用一特定预报模式和初条件计算由一预报模式系统得到的PDF。在预报开始的时候，PDF开始很狭窄，预报成员的初始离散度反映的是分析的不确定性。随着预报超前期增加，初始小扰动出现混沌增长，这使预报变得越来越不确定，并且在较短时间内对小尺度系统的可预报性不断消失，以后是大尺度系统的可预报性也消失^[12-13]。

集合预报是国际上的热门技术，但需要较大的计算条件。目前对于我国的省级或以下台站而言，一般很难具备适合这种超级集合巨大计算量的大型计算条件，而且各地区自身已经能够得到国内外大量的数值预报最终产品。以这些产品为基础，跳过模式本身的运算过程，仅利用好这些模式的结果直接进行集成，不失为一种实用且有效的方法，国际上通常把这种方法叫做“poor man's ensemble”(穷人的集合，PM)，实际上这也是一种多种模式的集成预报方法^{[12, 14]}。本文在此基础上，采用ECMWF模式、T213模式、HLAFS模式、JMH模式和MM5、GRAPES模式，动态地分析各种模式的近期误差，动态地分配各成员的权重，称之为“变权集成预报方法”。

2 几种变权集成预报方法的基本原理 2.1 误差概率递归训练变权法应用于格点场集成预报

对于数值预报的格点场，考虑到模式的整体预报能力，一般不对每一点进行权重分配，而是考虑某个区域的权重系数。另外，格点场数值预报原始模式如果具有一定的资料积累，可以适当考虑模式的历史误差问题。其基本原理如下：

设有m种模式作一种要素场预报，从中挑出三种模式，使其历史误差概率和实时误差概率较小。

各成员的历史误差概率：

$ {A_k} = {E_k}/\sum {{E_k}} $

(1)

式中E_k是区域的方差或标准差等能够表示数值产品质量的值，也可以是每一个格点的绝对误差值。A_k为某模式在各种模式误差中所占的比例，即概率权重。A_k的计算样本长度为所有历史资料，即它是历史误差概率。

各模式的实时误差概率：

$ {B_k} = {e_k}/\sum {{e_k}} $

(2)

B_k可以表示模式在近期某一时段的预报质量，为某模式在各种模式某一时段的预报平均误差总和所占比例。B_k计算样本长度可以根据短期天气周期来大致确定，一般可以取4～7。这就考虑了各模式的实时预报准确度。

因历史样本是固定的，故A_k是固定的。B_k则由于是近期取值，因而是变动的。对于既要考虑历史的又要考虑短期效果的模式误差概率，使用下式来计算综合误差概率：

$ {P_k} = C{A_k} + \left( {1 - C} \right){B_k} $

(3)

式中，C为常数，其值的变动代表考虑历史和实时误差的程度，C越大，历史成分为多，C小，则实时成分为多，如果没有历史样本，可以设C为0。针对不同要素，可以取不同的C值。各个模式都可以求出P_k，对于m种模式，则得到相应的综合误差概率：

$ P = \left( {{P_1},{P_2},{P_3} \cdot \cdot \cdot ,{P_m}} \right) $

(4)

式中P₁，P₂，P₃，…，P_m按其值大小由小到大排序。前三种模式即为优选出的预报效果较好的方法。由于B_k是变动的，因此P_k也是变动的，即在每一次应用中，得到的排序表是变动的，被选中的三种模式也是动态的。设选中的三种模式的综合误差概率为P₁、P₂、P₃，其对某一种要素在某一点的预报值为S₁、S₂、S₃，对其中任两种模式的预报值进行集成，如第一种和第二种，则有：

$ {S_{12}} = {P_{12}}{S_1} + {P_{21}}{S_2} $

(5)

式中S₁₂为此两种模式的集成优选点；

$ \begin{array}{l} {P_{12}} = {P_2}/\left( {{P_1} + {P_2}} \right)\\ {P_{21}} = {P_1}/\left( {{P_1} + {P_2}} \right) \end{array} $

(6)

为基于误差概率的第一种、第二种模式在集成中的权重系数，是归一化的。

用此方法两两集成，得到三个集成预报值S₁₂、S₁₃、S₂₃，然后再重新进行两两集成，记S₁₂、S₁₃、S₂₃为S₁′、S₂′、S₃′，其误差概率为：

$ \begin{array}{l} {P_1}\prime = \left( {{P_1} + {P_2}} \right)/2\\ {P_2}\prime = \left( {{P_1} + {P_3}} \right)/2\\ {P_3}\prime = \left( {{P_2} + {P_3}} \right)/2 \end{array} $

(7)

由式(5)、(6)、(7)得到新的预报值S₁′、S₂′、S₃′及P₁′、P₂′、P₃′，采用递归演算，反复式(5)、(6)、(7)，不断得到更新的S₁′、S₂′、S₃′，这三个值随着递归运算是逐步收敛的，因为两两集成记忆点永远落在两者之间, 当两个集成记忆点小于某个设定的限值时，停止集成。

2.2 滑动变权法用于离散点降水集成预报

该方法采用目前投入业务运行的数值模式产品，包括：T213、HLAFS、ECMWF、德国降水预报、日本降水预报、MM5、GRAPS产品和经定量化处理后的全国台站主观预报产品。具体工作原理是：

若以R表示集成预报值，则：

$ {{\bar R}_{j, t}} = \sum\limits_{i = 1}^n {{w_i}{, _j}{, _t}} {R_{i, j, t}} $

(8)

式中j为站点标号，t为预报时效，i为集成预报成员，n为成员个数，R_{j, t}为站点j在预报时效t的集成预报值，w_{i, j,t}为在j站点上，第i个成员在第t预报时效的权重系数，R_{i,j, t}为第i个成员在站点j上，t预报时段的降水预报值，其中w_{i, j,t}满足条件：

$ \sum\limits_{i = 1}^n {{w_i}{{_,}_j}{{_,}_t}} = 1 $

(9)

由式(9)可知，权重的分配不仅针对各个成员本身，并且具体到每个成员在不同站点、不同预报时段，权重的计算采用如下方法和步骤，取：

$ {E_{i,j,t}} = \frac{1}{K}\sum\limits_{k = 1}^K {\left| {{R_{i,j,t}} - {r_{j,t}}} \right|} $

(10)

r_{j, t}为站点j在预报时效t内的实况降水量，k=1, 2，…，K, 为连续滚动的预报天数，这样可得到连续K天某个集成成员在每个站点、各个预报时效的预报平均绝对误差E_{i, j, t}，再取其倒数：

$ {Q_{i, j, t}} = 1/{E_{i, j, t}} $

(11)

则权重系数为：

$ {w_{i, j, t}} = {Q_{i, j, t}}/\sum\limits_{i = 1}^n {{Q_{i, }}{_{j,t}}} $

(12)

显然，式(9)满足条件式(12)，各成员的权重系数会根据成员最近几天在不同区域、不同预报时段的预报效果进行动态变化和调整，可直观地解释为当某个成员连续K天在某个站点和预报时效内的预报误差最小(大)时，在集成预报中所占权重最大(小)。

由于集成预报最后的结果事实上是各成员在不同权重下的并集^[15]，在集成为确定性预报的时候，空报的现象随着成员间差异性或离散度的增大将更加显著。因此，必须采取一定的措施，来抑制空报的发生及其程度，以修正集成预报值。假定当实况无降水而预报降水量大于5mm时，定义为一次空报。于是，可统计出各成员在连续5天滚动预报中在各站点和各预报时效空报的次数和平均空报雨量M_{j, t}，并且规定当空报次数占预报总次数一定比例(实际业务中一般可取50%)以上时，用集成预报值减去平均空报雨量M_{j, t}。同时在有无降水的判定上，规定当三分之二以上成员预报有降水时，各成员再在设计的权重分配方案下进行集成预报，否则视为无降水。因此，修正后的集成预报值可写为：

$ {{\bar R}_{j, t}} = \beta \left( {\sum\limits_{i = 1}^n {{w_{i, j, \mathit{t}}}{R_{i, j, t}} - \gamma {M_{j, t}}} } \right) $

(13)

其中β=0或1，是有无降水判定因子，即：

$ \beta = \left\{ \begin{array}{l} 0\;\;\;\;{N_{有降水}}/{N_总} <\frac{2}{3}\\ 1\;\;\;\;{N_{有降水}}/{N_总} \ge \frac{2}{3} \end{array} \right. $

(14)

N为成员数。γ为消空因子，也为二元取值，其值确定于空报次数和预报总次数及其比例。

上述集成方法，真实地反映了某个成员在最近几天的降水预报能力，并据此进行动态分配权重的集成预报。由于短期天气系统一般具有4～7天的周期性特征，根据实际计算条件和业务的需求，取5天进行滚动。

2.3 集成平均法

集成平均是一种权重平均，美国国家环境预测中心进行集成预报统计时指出：“平均意义上的集成预报比任何单个预报要灵验，在冬季最好，夏季次之，甚至在季节转换过程亦有改善，因而集成平均是一条可行之路”^[16]。集成平均表面上总是较任何单个预报要“平滑”，可能确定内在可预报性。而其方法简单，易于操作，计算量较小，具有一定的实用性；实际上这种方法也是最为稳妥的，在预报评分上也不会太差，因为它产生的是一种并集的结果^[15]。但这种并集有可能会抹杀各成员的个性，因而可能存在较高的空报率，故一般不用于降水的预报，而可以用于几种性能相差不大的数值预报形势场的集合，这样可以节约很大的计算量，最快得到几种数值预报的平均场。

2.4 经验加权集成法

所谓经验加权法就是利用预报专家长期以来对数值预报产品的应用经验，用主观手段给各种数值预报加权。由于各模式采用的技术手段、建模时考虑的侧重点各不相同，同一模式在不同时期、不同区域的预报能力也不尽相同。比如某个成员在长江中下游预报出色，但在西北地区却不尽人意，而另一模式却恰好相反；或者某一模式在某地区冬季预报效果显著，而在夏季却差强人意，但另一模式对夏季强对流、暴雨等天气过程的预报能力突出，但对冬季冷空气的影响过程预报能力偏弱等等。在这种情况下，可能因为缺乏长期的质量评定资料，而预报员在日常预报中对各种数值预报产生了一定的应用经验，可以充分利用这些宝贵经验，让预报员主观给某种数值预报在某个区域、某个时间段进行干预，直接加权，产生经验加权的结果。这种方法加入了预报员的主观经验，实际上也是对数值预报的一种订正方法，在预报工作中应是可取的。

3 集成矩和集成簇 3.1 集成矩

集成矩是集成成员相对于集成平均的简单标准差，它反映出集成成员间总体变率程度，若具有较大的数值，表明个体预报结果在该处实质性的不谐，并且置信度较低，反之亦然。

3.2 特征线路图

特征线络图是从每一集成预报成员选择某一等值线，绘在同一张图上形成综合图，其显著的目的是以充分紧凑的形式提示每一集成预报的信息内容，以便可视和解释。这样就可提供与预报息息相关的信息，例如500hPa的588线、高压、低压位置，也可提供其他多种参数特征线图，有些有特殊用途，例如850hPa温度的“特征线络图”可用来预测边界层中的雨和雪、冻雨与非冻雨之间的不确定性等。

4 应用效果 4.1 降水集成预报

2005—2006年，将本文所研究的集成预报方法投入业务试验，应用表明，集成预报产品的降水预报比单一成员的预报准确率有明显提高。

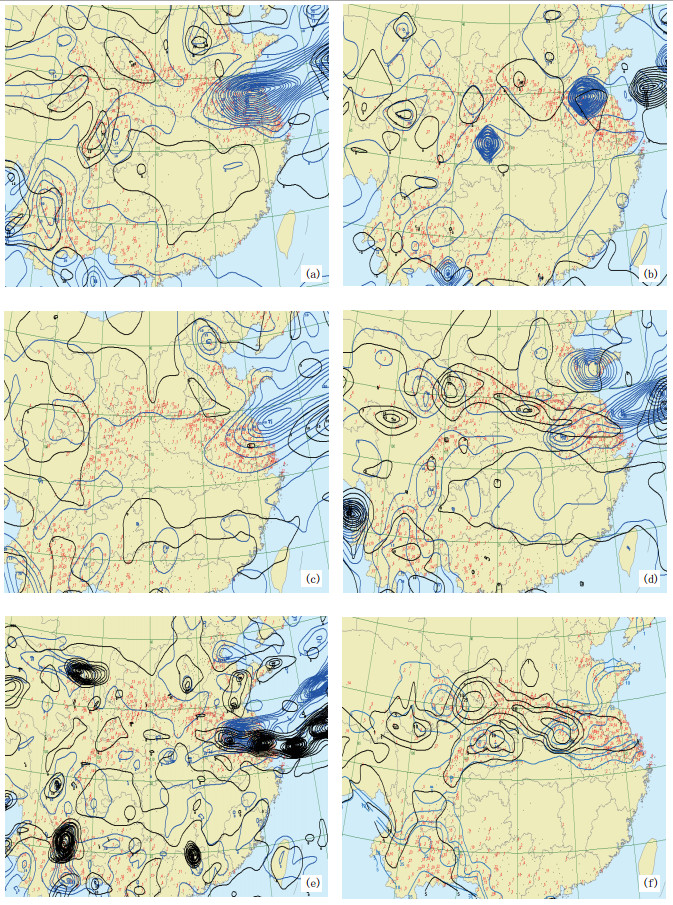
图 1(见彩页)为2006年7月1日08时至2日08时各种模式降水量累计预报以及集成预报对比。

从图 1可以看出，降水集成预报比任何一种单一的数值预报成员降水落区都有改善。从图 1还可以看出，对于本次降水过程，我国数值预报比国外数值预报的效果要好。如果采用固定权重进行集成可能会使我国模式的优势降低，势必影响到集成效果，而本文采用的是动态权重集成技术，可以动态地给各种数值产品分配权重，能够比较好地利用各种数值预报的优势，从而得到质量较好的预报产品。

选择江苏的苏北、苏中和苏南的部分站点对2005—2006年两年汛期降水的预报做了统计评分，TS评分结果为：徐州76%、淮安85%、泰州70%、镇江67%。可见，集成预报对苏北地区预报准确率均在70%以上，苏南和苏中降水预报准确率偏低，可能与台风降水量非均匀分布给各种模式带来的不稳定性有关，准确率还有待改进。

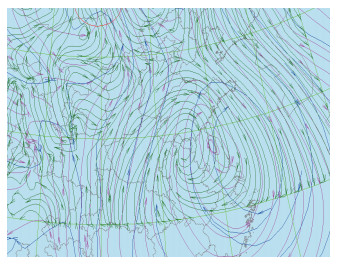
4.2 形势场和物理量集成预报

因集成预报保留了各家数值预报的优势，动态调整权重系数，对形势场的预报有明显的提高。通过2005—2006年的应用统计，对于东亚地区24小时、48小时500hPa高度场集成预报平均绝对误差在2hPa以内，96小时不超过4hPa，这在单一数值预报成员中是很难达到的。以2006年12月28日20时850hPa的流场集成产品为例(图 2，见彩页)，从集成产品和集成成员叠加显示可以看出，集成产品不受数值产品的数量、预报范围限制，而且产品不固定与哪一种数值预报接近(权重不固定)，集成预报的形势场或物理量场比大尺度的集成成员(如ECMWF)更为精细，能够反映出细微的天气系统。

4.3 冷空气集成预报

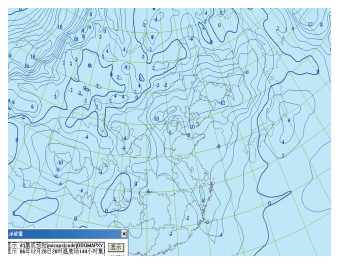
对于冷空气的预报，单一数值预报往往只能得出定性的预报，而本方法除了给出定性的温度场预报以外，还提供了客观化的降温幅度和降温区域(图 3，见彩页)，给预报员提供了很好的参考工具。2006年江苏共出现5次寒潮，用该方法提前72小时预报出4次，有一次降温区域报错，但降温趋势基本正确，预报准确率达80%。

5 结语

本文提出的集成预报方法是一种基于超级集合思想的简单经济的预报方法，它的最大优点在于集成成员权重系数的可变性，集成成员数量的不确定性以及集成产品的多样性。

(1) 针对不同形势场和物理量场的预报，提出了多种变权集成预报技术，包括误差概率递归训练变权法、滑动变权法等。通过动态分配权重改变了静态集成分配方案，能有效地反映各模式的预报能力变化，提高了不同要素、不同时效、不同地域的精细化预报水平。

(2) 变权集成方法不需要依赖长序列的历史样本，集成成员的个数具有可变性。集成产品不仅适用于某种特定的要素，而且可适用于不同层次的高度场、流场、相对湿度场、地面气压场集成、主要物理量的集成，并可以生成各种集成统计产品如集成矩、集成簇等。

(3) 动态权重集成技术，能够比较好地利用各种数值预报的优势，从而得到质量较好的预报产品。降水集成预报比任何一种单一的数值预报成员降水落区都有改善，集成产品预报更为精细，能够反映出细微的天气系统，客观化的降温幅度和降温区域预报以及多样的集成产品，给预报员提供了很好的参考工具。