引言

在研究和预测我国区域降水异常状况时，人们多从海气相互作用方面寻找联系^[1-5]。许多气象学者曾对太平洋和印度洋的海温对中国以及区域降水异常的影响做了大量的研究工作^[6-13]。然而，在与我国区域气候异常相关的因素中，SSTA只是其中之一^[14]。也有许多学者就青藏高原对于大气环流和天气气候的热力和动力作用进行了大量有重要价值的工作。叶笃正等^[15]早在20世纪50年代，就指出夏季青藏高原是一个巨大的热源，并从模拟实验分析了高原夏季加热作用对东亚大气环流尤其是南亚高压的重要影响。徐国昌、钱永甫、陈兴芳等^[16-18]曾分别分析了青藏高原积雪对我国大气环流和降水异常的影响。叶燕华^[19]、柏晶瑜^[20]曾分别研究了青藏高原感热与黄土高原以及长江中下游地区降水异常的关系，得出前期高原感热场的变化可作为后期降水异常的预测信号。这些研究主要是集中于青藏高原热力作用以及海气相互作用与大气环流及旱涝关系的认识，然而对于中国第一大流动沙漠——塔克拉玛干沙漠地表热力对大气环流以及区域降水异常影响方面的研究极少。

塔克拉玛干沙漠位于北半球中纬度欧亚大陆腹地，座落于新疆塔里木盆地中央，平均海拔高度在1000m以上，是世界第二、我国第一大流动沙漠，面积33.76×10⁴km²，该地区地表热力不仅对西北干旱区而且对北半球大气环流及天气、气候都有着重要影响，其物理机制一直是沙漠气象学研究的重点和难点。本文利用常规逐月降水资料和NCEP/DOE新再分析地表感热和潜热资料，采用SVD诊断方法首次分析了塔克拉玛干沙漠春、夏季地表热力与南疆夏季降水之间的配置模态和关系，进而建立了夏季降水异常前期的沙漠热力信号，为决策部门提供科学的依据，这对推动沙漠气象学的研究以及南疆农业生产具有十分重要的理论和现实意义。

1 资料与方法 1.1 资料

本文所用资料为塔里木盆地25个常规气象站(焉耆、库尔勒、乌什、阿克苏、拜城、新和、沙雅、轮台、库车、阿图什、乌恰、喀什、阿合奇、巴楚、岳普湖、柯坪、阿拉尔、英吉沙、麦盖提、莎车、叶城、皮山、策勒、和田、于田，见图 1)1979—2003年夏季(6—8月)逐月降水资料；同时期夏季和春季(3—5月)NCEP/DOE新再分析月平均地表感热和潜热通量资料，NCEP/DOE原始数据纬向分辨率为1.875°，经向为高斯格点。需要说明的是，NCEP/DOE地面通量资料属于同化资料中的C类资料，但是鉴于目前还缺少准确估算地面通量的有效途径和方法，因此，该资料仍然不失为研究陆面通量变化，尤其是研究长时间尺度变化的参考变量。在NCEP资料可信度验证方面，苏志侠，宋敏红，魏丽等^[21-23]曾分别对青藏高原地区NCEP热通量资料进行检验，发现月平均的再分析资料可以清楚地反映出该区域地面热源的气候特征。

1.2 方法

SVD(Singular Value Decomposition，简写为SVD)技术是用于研究两个气象要素场之间相互关系的重要诊断工具^[24-26]，它以两个场协方差最大为基础展开，分别计算交叉协方差矩阵的奇异值及正交的左、右奇异向量和时间系数，成对的奇异向量构成一对SVD空间模态。由于其计算简便，所得耦合信号的物理意义明确，特别适合气象场遥相关研究，近年来已被广泛应用于气候诊断研究中。

在实际应用中，设有两个气象要素场F(t)={F₁(t), F₂(t), L, F_p1(t)}(左场)，G(t)={G₁(t), G₂(t), L, G_p1(t)}(右场)，对这两个场的交叉协方差矩阵C_FG=FG^T根据条件极值进行分解来研究两者的相互关系，分解得：

$ {C_{FG}} = L\left| \begin{array}{l} \sum {\;\;\;\;\;\;\;0} \\ 0\;\;\;\;\;\;\;\;\;0 \end{array} \right|{R^T} $

其中∑=diag(λ₁, λ₂，L, λ_p)为对角阵，且λ_i＞0，i＝1，2，…，p，p是C_FG的秩，p≤min(p₁，p₂)，λ₁²，λ₂², L, λ_p²为C_FG^TC_FG的非零特征根，一般称λ_i为C_FG的奇异值，L为C_FG的左奇异向量，R为C_FG的右奇异向量，L和R均为正交矩阵。

分别对左右场构造新矩阵

$ A = {L^T}F\;\;\;\;\;\;\;B = {R^T}G $

式中A、B分别为左右场的时间系数。求得时间系数矩阵A、B之后，就可以定义每对奇异向量对应的时间系数之间的相关系数r_K(A, B)(K对应相应的模态)，它反映的是每一模态左右场相关的密切程度。

为了弄清楚塔克拉玛干沙漠地表热力异常与南疆夏季降水之间的关系，这里把塔里木盆地25站1979—2003年夏季降水作为右场，同时期塔克拉玛干沙漠夏季和前期春季地表感热、潜热分别作为左场，首先对左场和右场资料进行标准化，再用SVD方法分别得到夏季降水与前期(春季)及同期(夏季)感热、潜热成对的SVD模态(奇异向量)。考虑到应用SVD方法可能产生不真实的相关^[27]，本文采用Monte-Carlo检验法^[27-29]对SVD模态进行统计检验。

2 塔克拉玛干沙漠地表热力异常与南疆夏季降水的SVD分析

表 1给出了4种情况下前3对SVD模态(奇异向量)的方差贡献及模态相关系数。从表 1中我们可以看到，塔克拉玛干沙漠春、夏季地表感热、潜热与南疆夏季降水SVD分析的第一对奇异向量的方差贡献率均超过50%，且都远远高于第二、第三模态方差贡献率，说明第一空间型能解释足够多的左右场相关信息，所以本文仅分析各种情况下的第一对SVD模态和对应的时间系数。

2.1 塔克拉玛干沙漠夏季地表感热与同期南疆降水的主要耦合模态

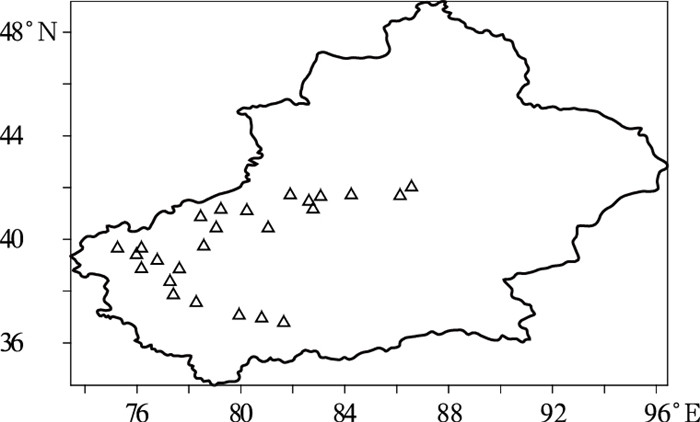
图 2a、2b是塔克拉玛干沙漠夏季地表感热与同期南疆降水SVD分析的第一对奇异向量，其方差贡献占总方差的63.49%，通过了α=0.05的Monte-Carlo显著性水平检验，模态时间相关系数为0.732。由此看到，第一对奇异向量的方差较大，能很好地表征沙漠夏季地表感热与南疆降水之间的耦合关系。从感热场(图 2a)可以看出，除了沙漠东部、南缘以及西部个别地区为正异常以外，沙漠主体大部分地区为负异常，尤其在38°~40°N、78°~82°E区域内，存在负异常的最大值区，中心值为－0.3。相应的沙漠夏季降水模态如图 2b所示，它表现为南疆降水一致为正异常，大值中心分布在南疆的西部和西北部地区。这表明，当塔克拉玛干沙漠尤其是38°~40°N、78°~82°E区域夏季地表感热异常偏小(偏大)时，对应南疆大部分地区降水异常偏多(偏少)，其中以南疆西部和西北部降水异常偏多(偏少)最为显著。

通过上面的分析发现，塔克拉玛干沙漠主体大部分地区一致的地表感热负异常对应着南疆降水一致的正异常，充分说明了该区域地表感热场和降水场异常变化相反的对应关系。图 2c是第一对左、右奇异向量对应的时间系数，两者之间的相关系数达0.732, 通过0.05显著性水平检验。由图可以看出，第一对奇异向量对应的时间系数变化情况基本一致，但振幅不尽相同，沙漠地表感热场变化幅度小于南疆降水场。

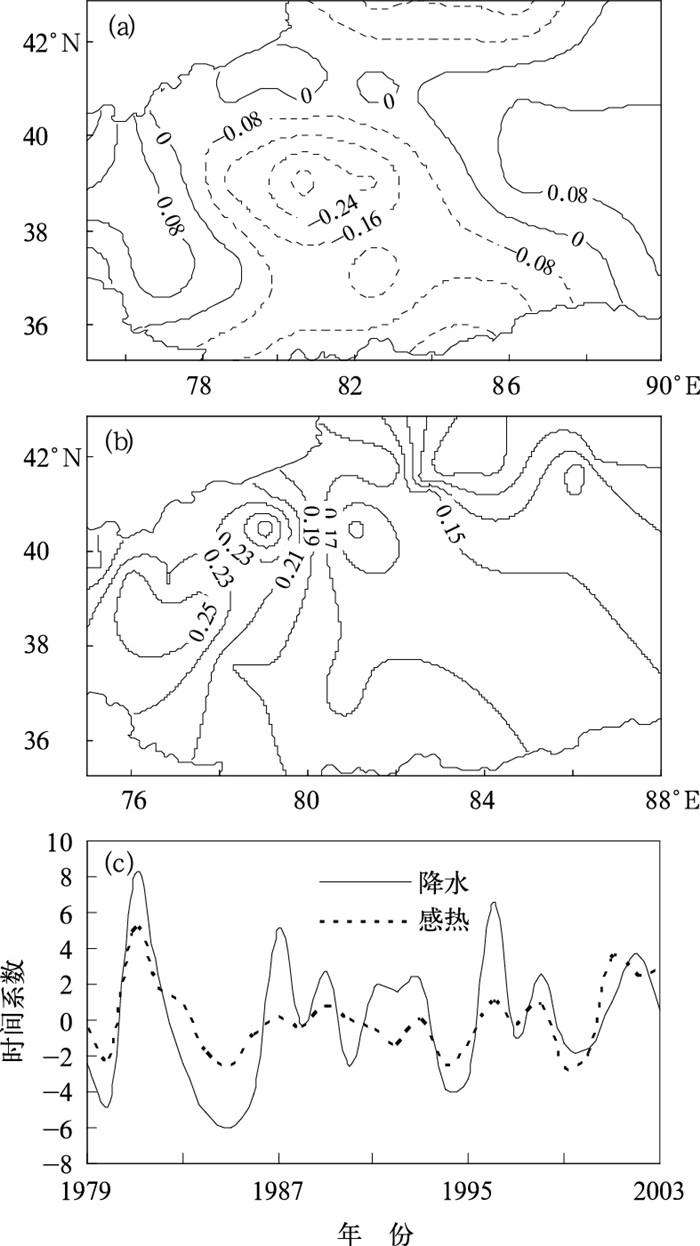
2.2 塔克拉玛干沙漠春季地表感热与南疆夏季降水的主要耦合模态

为了提取塔克拉玛干沙漠感热场对南疆夏季降水异常具有预测意义的前期热力信号，我们对春季感热场与夏季降水场进行SVD分析。图 3a、3b是经SVD分解后的第一对奇异向量，其方差贡献百分率为57.51%，同样也通过了α=0.05的Monte-Carlo显著性水平检验，模态时间相关系数为0.712，这说明前期春季沙漠地表感热场和后期夏季南疆降水场具有较好的非同步时空相关，其第一模态代表了两场相互耦合作用的主要特征。

从两场第一模态空间分布(图 3a、3b)看到，在降水场上(图 3b)，南疆夏季降水一致为正异常，大值中心仍然分布在南疆的西部和西北部地区。相应的沙漠春季感热模态如图 3a所示，自西向东呈现出“＋－＋”的空间分布特征，除了沙漠东部和西部部分地区为正异常以外，沙漠主体大部分地区为负异常，在38°~40°N、79°~83°E区域内，存在负异常的最大值区，中心值为－0.3。这表明，当塔克拉玛干沙漠尤其是38°~40°N、79°~83°E区域春季地表感热异常偏小(偏大)时，对应南疆大部分地区夏季降水异常偏多(偏少)，并以南疆西部和西北部降水异常偏多(偏少)最为显著。

由此可见，塔克拉玛干沙漠春季地表感热分布同样与南疆夏季降水存在着相反的对应关系，这与夏季感热和降水的变化关系是一致的。图 3c是第一对模态对应的时间系数，由图可以看出，两者变化趋势非常一致，相关达0.712, 具有明显的非同步联系。

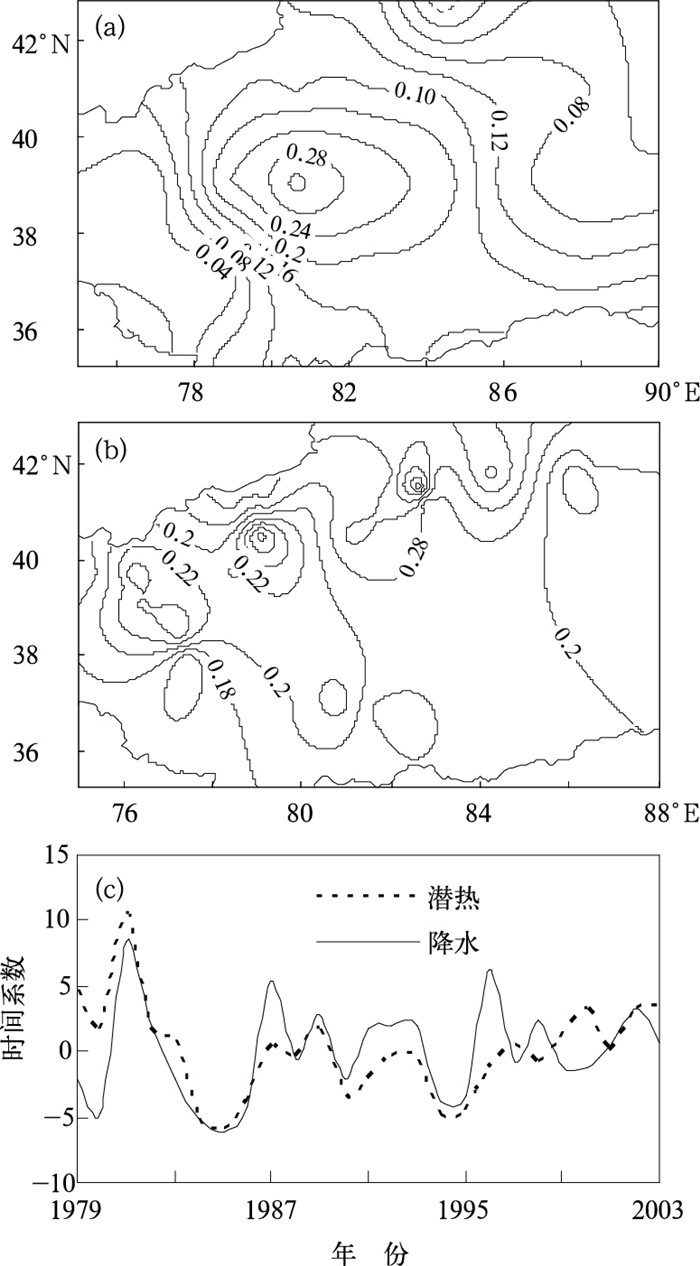
2.3 塔克拉玛干沙漠夏季地表潜热与同期南疆降水的主要耦合模态

图 4a、4b是塔克拉玛干沙漠夏季地表潜热与同期南疆降水SVD分析的第一对奇异向量，其方差贡献百分率为79.3%，这说明第一对奇异向量收敛速度较快，是夏季地表潜热场与同期降水最主要的耦合相关模态，其潜热场的主要特征是：整个沙漠呈现出一致性的空间分布，均为正异常，并且在沙漠的中部有一个正值中心，最大值为0.32。与此异常加热型相对应的降水空间分布特征是：南疆盆地也为一致的正异常，大值中心分布在南疆的西部和西北部地区，其值为0.24。这表明，当塔克拉玛干沙漠尤其是中部地区夏季地表潜热异常偏大时，南疆夏季降水异常偏多，并以西部和西北部地区降水异常偏多最为明显；反之亦然。从第一对奇异向量的时间系数(图 4c)可以看出，两个场的相关程度较高，模态时间相关系数达0.589，左、右奇异向量对应的时间系数变化情况基本一致，几乎呈同位相变化，严重的旱涝年在图上均能有所反映。

2.4 塔克拉玛干沙漠春季地表潜热与南疆夏季降水的主要耦合模态

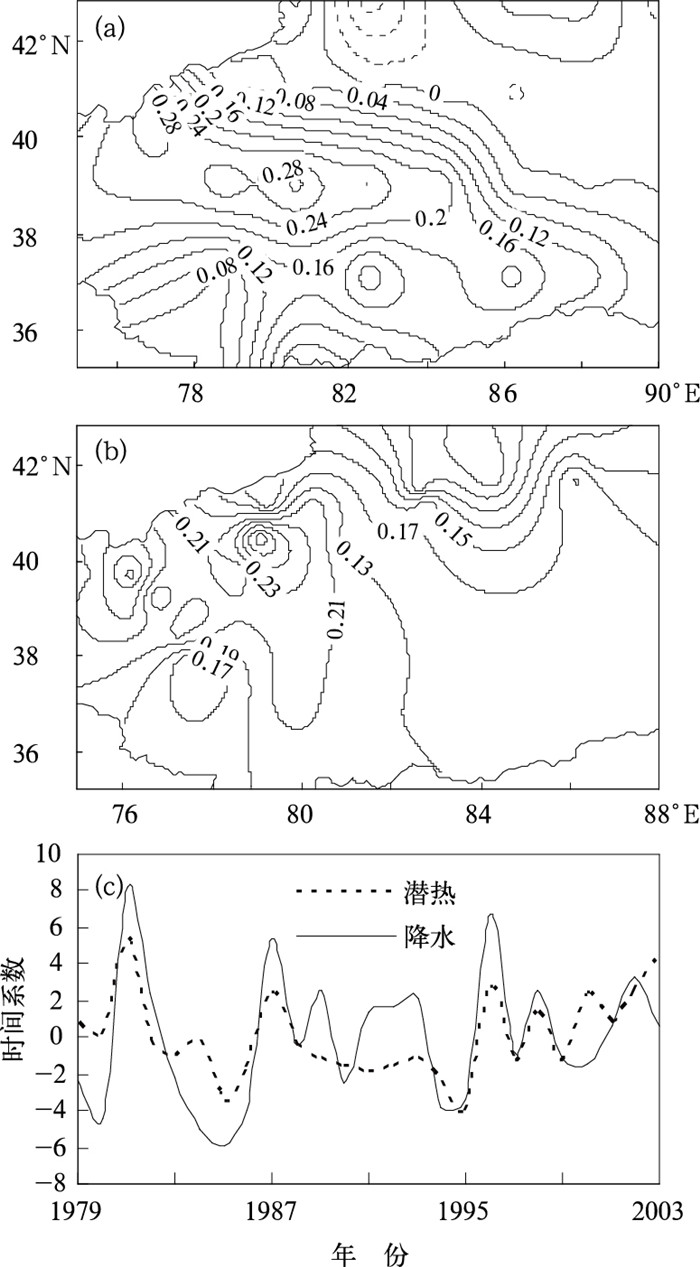
同样为了获取沙漠潜热场对南疆夏季降水异常具有预测意义的前期热力信号，我们对春季潜热场与夏季降水场也进行了SVD分析。图 5a、5b是沙漠春季地表潜热与南疆夏季降水SVD分析的第一对奇异向量，方差贡献率达到59.64%，其潜热场的主要特征与夏季潜热场相似，除沙漠北部有个别负相关区外，其他沙漠区均为正异常，大值中心分布在沙漠的中西部地区，最大值为0.28。与此异常加热型相对应的南疆降水空间分布仍然表现为全区一致性的特征，均为正异常，西部和西北部地区为大值中心，值为0.24。这说明，沙漠中西部地区春季地表潜热异常偏大时，南疆盆地夏季降水异常偏多，尤其是以西部和西北部地区降水偏多最为明显；反之亦然。从第一对奇异向量的时间系数(图 5c)也可以看出，两个场的相关程度较高，左、右奇异向量对应的时间系数变化情况基本一致。

3 结论与讨论

通过对塔克拉玛干沙漠春、夏季地表感热、潜热与南疆夏季降水进行SVD分析，我们可以得出以下几点结论：

(1) 沙漠地表热力场与南疆降水场的第一模态代表了两场间的主要耦合特征，具有较好的时空相关，其中南疆西部、西北部地区和沙漠中部偏西偏北区域(37°~40°N、78°~83°E)为SVD耦合相关的显著区域。

(2) 沙漠春、夏季地表感热场与南疆夏季降水场SVD分析的第一模态表明：地表感热和降水呈负相关关系，当沙漠主体大部分地区感热异常偏小(偏大)，并以沙漠中部偏小(偏大)最为明显时，对应南疆夏季降水异常偏多(偏少)，其中南疆西部和西北部地区降水偏多(偏少)最为显著。

(3) 沙漠春、夏季地表潜热场与南疆夏季降水场SVD分析的第一模态表明：地表潜热和降水呈正相关关系，当沙漠整体潜热异常偏大(偏小)，并以沙漠中部偏大(偏小)最为明显时，对应南疆夏季降水异常偏多(偏少)，其中南疆西部和西北部偏多(偏少)最为显著。

(4) 前期春季塔克拉玛干沙漠地表感热、潜热异常变化可作为未来夏季南疆降水异常具有指示意义的一个信号，在作降水的长期预测时应重视前期沙漠地表感热和潜热的变化状况。

需要说明的是，塔克拉玛干沙漠下垫面较为均一，从而使得沙漠地表感热和潜热分布也具有整体的一致性特征，加之南疆盆地年降水量较少，降水变率大，因此沙漠热力场与南疆降水场之间的相关程度相对于其他地区较小。此外，塔克拉玛干沙漠地表感热和潜热代表了沙漠的热力状况，尤其在春季和夏季，沙漠表面与大气之间存在着强的能量交换，前期地表感热和潜热的持续性异常可能会造成大气环流的异常变化，从而导致后期降水的异常。本文仅对沙漠地表热力与南疆夏季降水之间的关系运用SVD技术进行了初步的分析，至于沙漠热力异常对降水异常的影响机理及动力学机制，还需今后作进一步的分析和研究。