引言

SWAT(Soil and Water Assessment Tool)模型是由美国农业部(USDA)的农业研究中心(ARS)研发的，比较适用面向水资源管理的长时段的分布式水文过程模拟。SWAT模型于20世纪90年代早期正式推出，ARS在1998年发布了SWAT与GIS软件(如GRASS、Arcview)的集成版本^[1]。SWAT模型的有效性已经得到了国内外许多研究项目和研究者的证明^[2-8]，并已广泛地应用于美国国家项目HUMUS(Hydrological Unit Modeling of United States)。SWAT模型在我国的应用和植入研究刚刚起步，还很薄弱。国内学者杨桂莲、郝芳华等基于SWAT模型与数字滤波技术对河南洛河流域的径流中的基流进行估算和比较，结果表明模型对基流的模拟有较高精度^[5]。张雪松在卢氏流域(4623km²)应用SWAT模型进行中尺度流域的产流产沙模拟试验，得出模型在长期连续径流和泥沙负荷模拟中具有较好的适用性^[6]。胡远安等的研究也证明SWAT能够有效地模拟长时间序列的水文过程^[7]。朱利应用SWAT模型研究了汉江上游区径流对气候变化的响应，指出汉江上游区的降水变化对水资源的影响大于气温变化对水资源的影响^[8]。本文利用SWAT模型模拟整个汉江流域1971—2000年逐月径流，分析该流域水量平衡状况、径流变化及其对降水变化的响应，为汉江流域的水资源管理与研究提供一种新的有效方法。

1 研究区域概况

汉江是长江中游的重要支流，发源于秦岭南麓，流经陕西、甘肃、四川、河南、湖北五省。其干流流经陕西和湖北两省，于武汉市汇入长江，全长1577km，落差1964m，流域面积15.9×10⁴km²，流域水系呈叶脉状，支流众多^[9-10]。汉江流域属于北亚热带边缘湿润季风气候区，由于受秦岭、米仓山、巴山地形的影响，同时兼有暖温带和中温带山地气候的特征，气候温和，四季分明，雨量较充沛(多年平均达960mm左右); 降水年内分配不均，每年5—9月的总降水量占全年降水量的70%；降水年际变化大，无霜期长。汉江流域径流补给以降水形成的地表径流为主(多年平均达249.28mm)，地下径流为次(多年平均达154.72mm)，径流分布规律为南多北少，山地多川道盆地少。径流年内分配不均，夏秋多，春冬少；径流多年变化过程与降水多年变化过程基本一致。

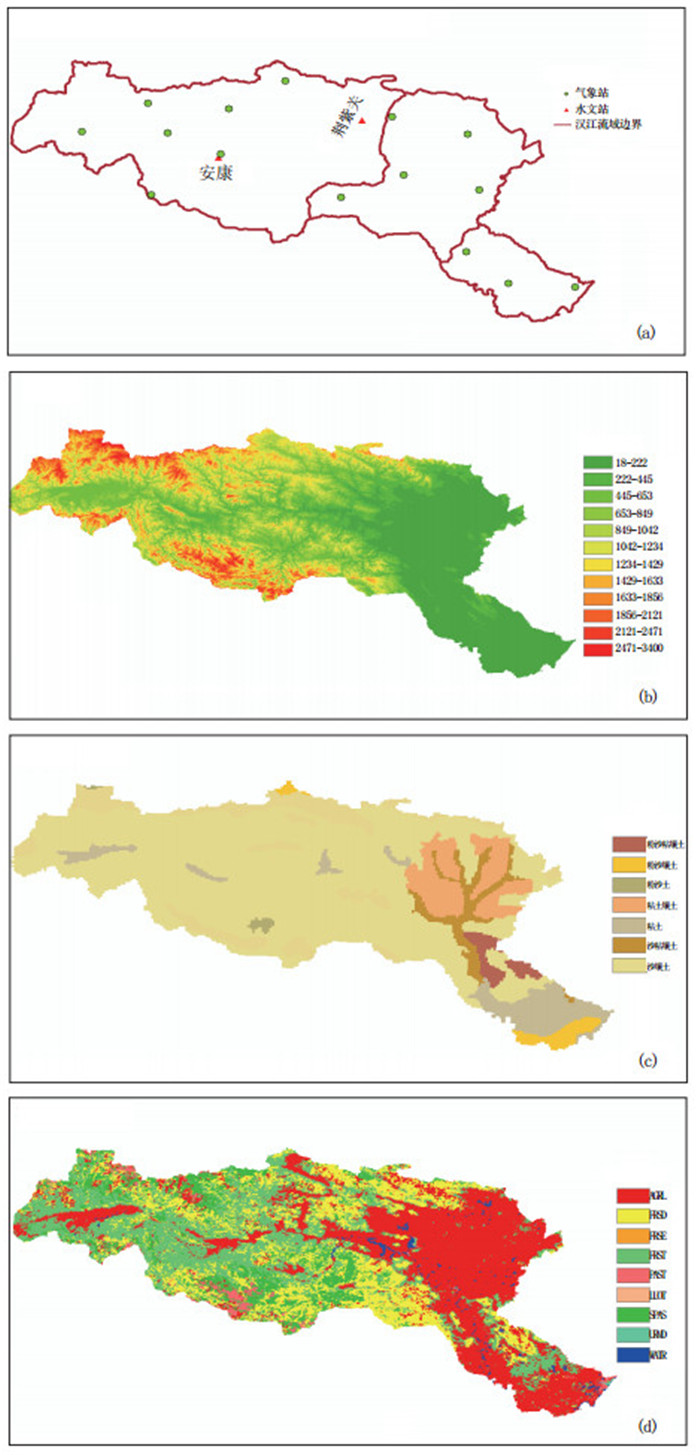
2 资料收集与处理 2.1 气象观测数据

汉江流域气象数据来源于中国气象局国家气象信息中心，包括15个气象台站(图 1a，见彩页)的1971—2000年逐日气温(平均、最高、最低)、降水、相对湿度、风速等气象要素，用于驱动SWAT水文模型进行径流模拟。

2.2 流量数据

流量数据来源于水利部水文局，包括1983、1985年荆紫关水文站(位于汉江上游支流，33.25°N、111.02°E)逐月平均径流量，2000年安康水文站(位于汉江上游干流，32.67°N、109.00°E)逐月平均径流量，上述水文站点分布如图 1a(见彩页)。其中，1983年荆紫关站逐月径流量数据用于率定SWAT模型的参数，1985年荆紫关站以及2000年安康站逐月径流量数据用于检验模型模拟精度。

2.3 地理空间数据 2.3.1 数字高程模型

DEM数据来源于国家1:25万基本比例尺地形图，空间分辨率重采样为1km×1km(图 1b，见彩页)。利用Arcview的空间分析功能提取水流方向、水流长度、河流网络、划分子流域以及水文模拟单元，计算地形因子，获取SWAT模型所需要的地形、水系、汇流区域等信息。

2.3.2 土地利用覆盖数据

土地利用覆盖数据来源于美国地质调查局(USGS)1976年获取的土地利用覆盖栅格图，空间分辨率为1km×1km，在汉江流域内分布有15种类型。根据USGS Land Use/Land Cover System与SWAT模型中土地利用覆盖分类标准的对应转化关系重新分类，获得符合SWAT土地利用覆盖分类标准的9种类型(图 1d，见彩页)。

2.3.3 土壤数据

土壤数据来源于中国地图出版社1978年出版的中国土壤分类基础图，比例尺为14000 000，在汉江流域内分布有11种土壤类型。考虑到汉江流域土壤属性特征以及SWAT模型中土壤物理特性的美制标准，在采纳前人的经验和知识的前提下^[11-12]，将一些物理特性近似或者面积较小的类型归为同一类型，在原分类基础上对土壤进行重分类，重分类后的汉江流域土壤类型有7种, 分别是粘土(NT)、粘壤土(NRT)、沙粘壤土(SNRT)、沙壤土(SRT)、粉沙壤土(FSRT)、粉沙粘壤土(FSNRT)和粉沙土(FST), 如图 1c(见彩页)所示。

2.4 定制WGEN

WGEN(Weather Generator)是根据气象因子随时间变化所遵循的随机过程，弱稳定过程等数理统计原理，通过平均气象数据来模拟周期性的日气象数据变化过程^[13-14]。SWAT模型通过与WGEN的耦合来完成气象数据序列的补缺，可以实现气象数据不全或者缺失地区的水文过程模拟。本研究中需要输入的多年月平均气象统计数据共有14类168个，分别为月平均最高气温及相应标准差、月平均最低气温及相应标准差、降雨天数、降雨偏度系数、降雨干湿概率和湿湿概率、月最大半小时降雨量、月平均太阳辐射、露点温度及风速。上述数据的统计计算工作量比较大且繁琐，因此，在实际的WGEN数据准备过程中，根据各输入数据的统计方法，利用Microsoft SQL编写存储过程读取长时段气象数据，快速计算天气发生器所需的气象统计数据。在此基础上利用WGEN和气象要素实测数据建立SWAT模型气象数据库，模拟出模型运行所需的气象驱动资料。

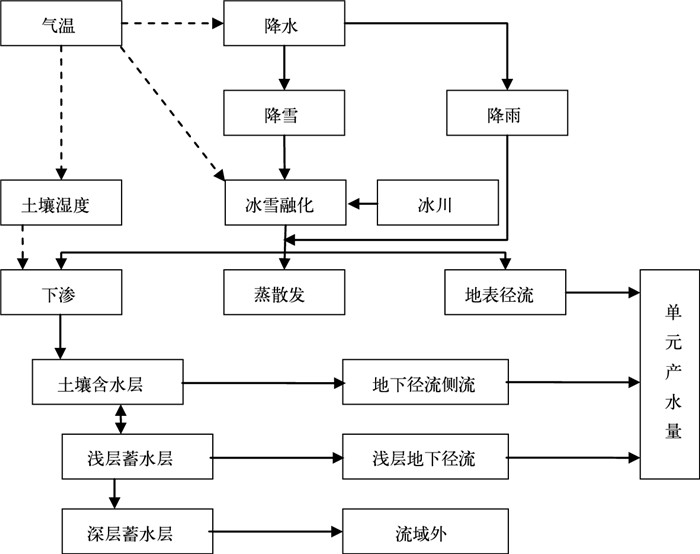
3 SWAT模型产流模拟原理

SWAT模型的产流模拟不同于一般的统计模型，它具有很强的物理机制^[15]，气温控制降水形态、冰雪融化、蒸散发、地下径流补给等物理过程，并最终导致产流量的变化，SWAT模型中产流过程如图 2所示。该模型采用SCS方法^[16]和Green&Ampt^[17]入渗方法计算地表径流。在计算蒸散发时，考虑水面蒸发、裸地蒸发和植被蒸发，并分开模拟土壤水蒸发和植被蒸腾。潜在土壤水蒸发由潜在蒸散发和叶面积指数估算，实际土壤水蒸发用土壤厚度和含水量的指数关系式计算，植物蒸腾由潜在蒸散发和叶面积指数的线性关系式计算，并提供3种潜在蒸散发计算方法(Penman-Montieth法^[18]、Priestley-Talor法^[19]、Hargreaves法^[20])供选择。壤中流采用动力贮水模型^[21]计算，考虑水力传导度、坡度和土壤含水量的时空变化。

4 实例研究

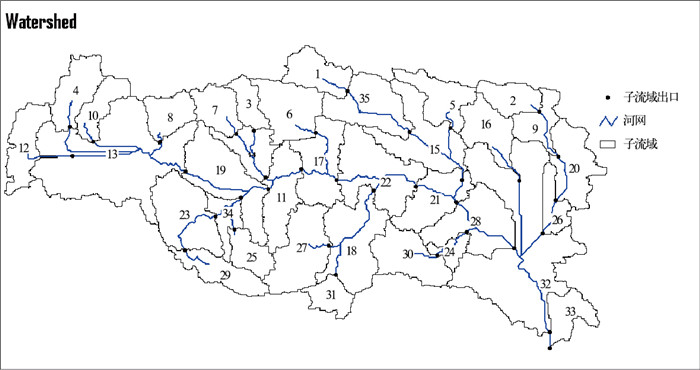
输入研究区域水文气象资料、土地利用覆盖资料、土壤类型资料、DEM资料以驱动SWAT2005运行，在研究区域内共提取35个子流域，129个水文响应单元(HRUs)，提取的集水区面积为126683km²(如图 3所示)。在划分子流域内水文响应单元时，土地利用覆盖类型占子流域面积阈值取10%，土壤类型占土地利用覆盖面积阈值取值10%。采用SCS法计算地表径流，Penman-Montieth法计算潜在蒸发，模拟1971—2000年汉江流域逐月径流。

4.1 参数敏感性分析与率定

选取27个模型输入参数进行参数敏感性分析试验，设置参数值采样间隔为10，每次参数变化值为0.05，利用AVSWAT2005自动敏感性分析工具进行了280次比较判断，选取了敏感性等级最高的6个参数(如表 1所示)进行模型率定。

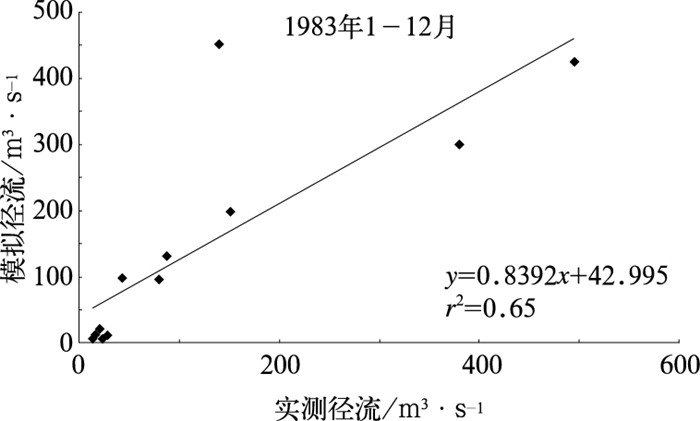
利用1983年荆紫关站逐月流量序列对月径流模拟进行率定，根据“先调整水量平衡，再调整过程；先调整地表径流，再调整土壤水、蒸散发和地下径流”的原则^[22]，首先调整CN₂、SOL_AWC、ESCO来拟合地表径流，随后调整GW_REVAP、REVAPMN、GWQMN来拟合基流。参数率定结果如表 1所示。

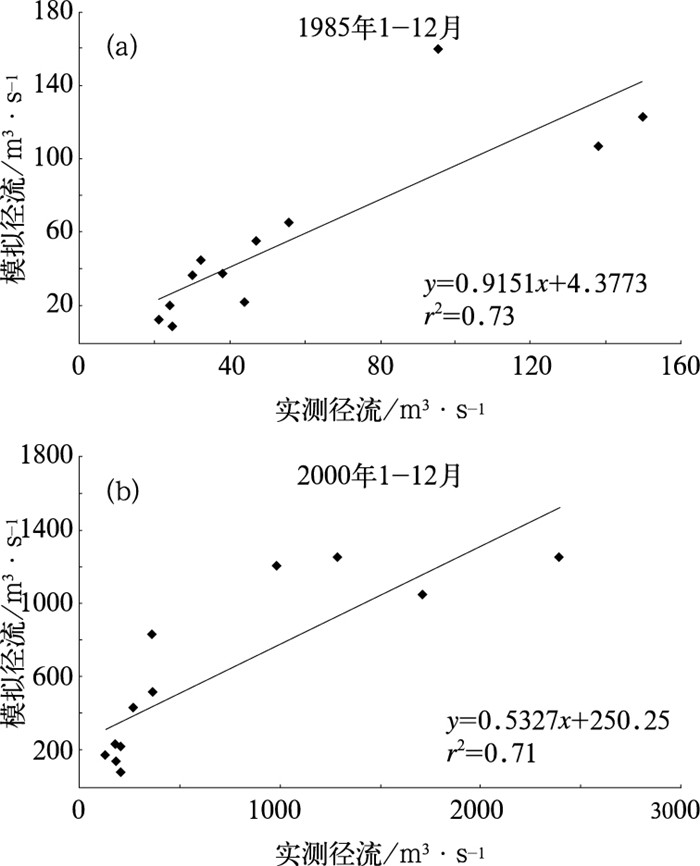
4.2 径流模拟验证

利用荆紫关站1985年和安康站2000年逐月流量数据进行模型验证，并采用Nash-Sutcliffe模拟效率系数Ens和相关系数r²对模型的验证结果进行评价。Nash-Sutcliffe越大，相关系数r²越高，表明模拟效率越高。如果Ens＜0，说明模型模拟值比实测值可信度更低，通常取Ens＞0.5作为径流模拟效率的评价标准^[23]。r²越接近1，说明模拟径流量与实测径流量越接近(模拟径流对实测径流的解释度越高)，通常取r²＞0.6作为径流模拟与实测值相关程度评价标准。

荆紫关站率定期，荆紫关站和安康站验证期月径流模拟效率及拟合情况见表 2、图 4、图 5。模型效率系数Ens、相关系数r²值表明，SWAT模型适用于模拟汉江流域径流变化。

Nash-Sutcliffe系数：

$ Ens = 1 - \frac{{\sum\limits_{i = 1}^n {{{\left( {{Q_{{\rm{obs}}, i}} - {Q_{{\rm{sim}}, i}}} \right)}^2}} }}{{\sum\limits_{i = 1}^n {{{\left( {{Q_{{\rm{obs}}, i}} - {{\overline Q }_{{\rm{obs}}}}} \right)}^2}} }} $

(1)

相关系数：

$ {r^2} = \frac{{{{\left[{\sum\limits_{i = 1}^n {\left( {{Q_{{\rm{obs}}, i}}-{{\overline Q }_{{\rm{obs}}}}} \right)\left( {{Q_{{\rm{sim}}, i}}-{{\overline Q }_{{\rm{sim}}}}} \right)} } \right]}^2}}}{{\sum\limits_{i = 1}^n {{{\left( {{Q_{{\rm{obs}}, i}} - {{\overline Q }_{{\rm{obs}}}}} \right)}^2}} \sum\limits_{i = 1}^n {{{\left( {{Q_{{\rm{sim}}, i}} - {{\overline Q }_{{\rm{sim}}}}} \right)}^2}} }} $

(2)

其中，Ens为Nash-Sutcliffe效率系数；r²为相关系数平方；Q_{obs, i}为天然流量；Q_{sim, i}为模拟流量；Q_obs为多年平均天然流量；Q_sim为多年平均模拟流量；n为模拟流量序列长度。

4.3 模拟径流结果分析

通过模型检验后，对1971—2000年30年逐月径流量进行了模拟，分析了汉江流域的水量平衡以及径流变化情况。

4.3.1 汉江流域水量平衡分析

流域的水循环过程对水量水质状况产生重要影响，对于生态环境的可持续发展有着重要作用，而流域水量平衡各分量特别是支出项的观测比较困难，探求流域内各水量的分配，需借助模型模拟的研究手段^[24-25]。作者借助SWAT模型对汉江流域30年月、年水量平衡进行了分析，其水量平衡方程如下。

$ \begin{array}{l} PREC = SURQ + PERCOLATE + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;LATQ + ET + \mathit{\Delta }S \end{array} $

(3)

式中, PREC为降水量(mm)，SURQ为地表径流量(mm)，PERCOLATE为土壤对地下水补给量(mm), LATQ为地下侧流量(mm)，ET为实际蒸散发量(mm)，ΔS为土壤含水量变化(mm)。

(1) 1971—2000年月平均水量平衡分析

汉江流域1971—2000年1—12月30年平均的水量平衡分析结果(如表 3)表明，30年月平均降水量为80.27mm，地表径流量为20.77mm，土壤对地下水补给量为14.16mm，地下水侧流量为0.20mm, 实际蒸散发量为44.93mm，土壤含水变化量0.21mm；月平均蒸散发量、地表径流量、土壤对地下水补给量、土壤含水变化量、地下水侧流量分别占降水量的55.97%、25.88%、17.64%、0.26%、0.25%，蒸散发量是该流域水量的主要输出项；按季节划分，流域地表径流量、土壤对地下水补给量、地下水侧流量、实际蒸散发量、土壤含水变化量的最大值分别在夏季(146.05mm)、秋季(68.63mm)、秋季(0.71mm)、夏季(311.66mm)、秋季(37.5mm)；最小值分别在冬季(2.43mm)、冬季(17.71mm)、春季(0.51mm)、冬季(23.23mm)、冬季(2.16mm)。

(2) 1971—2000年30年年平均水量平衡分析

如表 4所示，汉江流域30年年平均降水量为963.22mm，地表径流量为249.28mm，土壤对地下水补给量为169.93mm，实际蒸散发量539.10mm，土壤含水变化量2.48mm；蒸散发是该流域水量的主要输出项，年均蒸散发量占年均降水量的55.97%，但是年际变化不大(年均变化率为5%)；地表径流占年均降水量的25.88%，受降水影响地表径流年际变化较大(年均变化率为41%)；年均土壤对地下水补给量占降水量的17.64%，土壤对地下水的补给量与降水量关系密切，呈正相关关系，并直接影响基流量的大小；年均土壤含水变化量占降水量的0.26%，土壤含水量年均变化率为0.16%，符合长时间序列土壤剖面水量变化特征。

4.3.2 对1971—2000年30年径流月变化的模拟

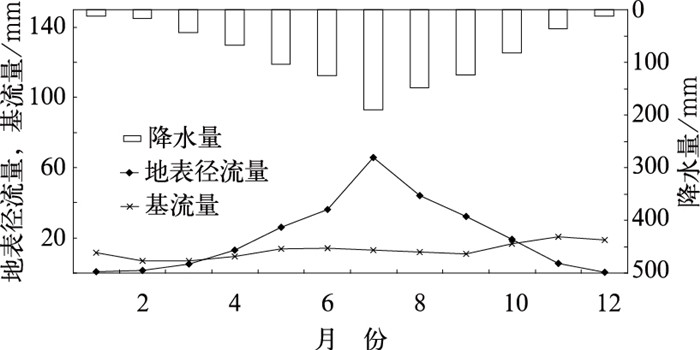
1—12月30年平均径流模拟结果(如图 6)表明，30年月地表径流量5—9月多，1—4月、10—12月少；地表径流量月变化趋势与降水量月变化趋势较一致，从年初开始递增，7月达到最大值后开始减少；月基流量与月降水量无明显相关关系；各月30年平均降水量、地表径流量最大值均在7月，各月30年平均基流量最大值出现在11月；各月30年平均降水量、地表径流量最小值出现在12月，各月30年平均基流量最小值出现在2月；月地表径流量对降水量的响应程度高于月基流量。

各月30年平均地表径流量月变率均值高于基流量月均变化率，分别为0.95、0.22。地表径流量月变率与降水量月变率变化较一致，基流量月变率与降水量月变率无明显相关关系；各月30年平均降水量、地表径流量、基流量月变化率最大值分别为1.53、2.75、0.52，分别出现在3月、3月、10月；最小值分别为0.16、0.28、0.01，分别出现在9月、9月、3月；地表径流量月变率对降水量月变率的响应较明显。

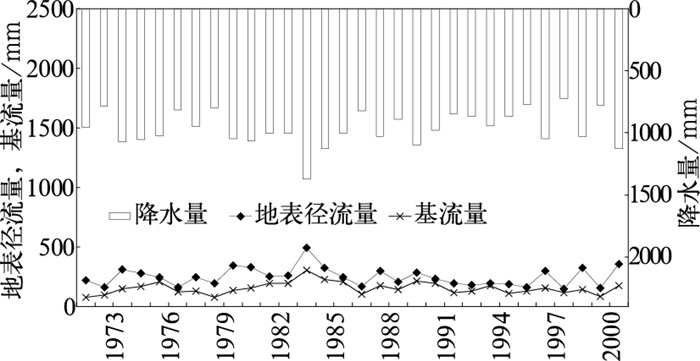
4.3.3 对1971—2000年30年径流年变化的模拟

如图 7所示，30年年平均地表径流深(249.28mm)是基流深(154.72mm)的1.6倍。30年年地表径流量与降水量、基流量最大值出现的年份一致，均在汉江流域的丰水年1983年。30年年地表径流量与降水量最小值出现的年份一致，均在汉江流域枯水年1997年；而基流量最小值出现在1971年。降水多的年份，地表径流量、基流量较高；降水较少的年份，地表径流对降水的响应程度比基流对降水的响应程度高。

30年流域地表径流量、基流量的年变化趋势与降水量年变化趋势基本一致，年均变化率分别为0.41、0.33、0.18，地表径流量年变化率最高，降水量年变化率最低。地表径流量与降水量年变率的变化趋势基本一致，基流量与降水量年变率的变化趋势在个别年份相反，如1994年、1995年、1997年、1999年(上述4年份的年降水量均小于30年年均降水量，为汉江流域降水偏少年)。年流域降水量、地表径流量、基流量量变化率最大值分别为0.45、1.31、1.07，均出现在2000年，降水量年际变化率高时，径流变化对降水变化响应较明显；最小值分别为0.00、0.02、0.01，分别出现在1982年、1994年、1982年，降水量年际变化率低时，径流变化对降水变化响应不明显。

5 总结与讨论

(1) 利用SWAT模型模拟了汉江流域径流过程，模拟精度达到了评价标准，说明SWAT模型较适合于汉江流域径流模拟。

(2) 1971—2000年30年月、年平均水量平衡分析结果表明，月、年平均蒸散发量、地表径流量、土壤对地下水补给量、土壤含水变化量、地下水侧流量分别占降水量的55.97%、25.88%、17.64%、0.26%、0.25%，蒸散发是该流域水量的主要输出项。

(3) 汉江流域各月30年(1971—2000年)平均降水量变化趋势与地表径流量的变化趋势较一致，而月基流量与月降水量无明显相关关系。

(4) 汉江流域1971—2000年30年流域降水量年变化趋势与地表径流量、基流量的变化趋势较一致。

(5) 1971—2000年30年月、年地表径流量对降水量的响应程度比基流量对降水量的响应程度高。

尽管SWAT模型的模拟效率高于评价标准，但模拟效率仍然不高，这与模型采用的土地利用、覆盖、土壤数据的时空局限性以及流域集水区范围有关。因此，采用多种水文评估模型(如SWIM、Topmodel、HBV)，根据不同时期的下垫面信息分时段分流域模拟径流，以期进一步提高模拟效率，找到更适合于汉江流域径流模拟的水文模型是今后努力解决的问题。