引言

随着气象科学技术的发展，以数值预报为基础的天气预报的准确率不断提高，这也使许多气象用户对气象预报提出了更高的要求，因此“三定预报”(定点、定时、定量)应运而生，并成为提高气象预报准确率的新追求和气象用户更高的要求^[1]。从气象服务的需求而言，“三定预报”的要求是可以理解的。然而，基于我们对大气系统的高度非线性和混沌性的科学认识^[2-3]，我们需要更加谨慎地思考“三定”预报问题。很显然，“三定”预报也就是100%确定的预报，与气象预报不确定性的科学本质是相悖的，也会误导和影响公众和气象用户科学的使用和决策，使气象部门招致公众和用户的指责。本文引用了一位公众自发地对气象预报评估的事例，通过对此事例的分析，我们可以了解并认识公众和用户对于天气预报关注的内容和要点，以及他们是如何看待和评价预报的准确性等问题，并由此提出了我们应该逐步改变天气预报发布服务方式的问题。叶笃正等^[4]不久前也对此有过讨论。如果天气预报既能让公众和气象用户知道预报的结论是什么，也能清楚预报的可信度如何，就能使公众和用户能够根据预报的不确定性程度以及自身对气象条件的依赖程度来科学地使用天气预报决策，从而达到最佳的使用效果^[5]。本文提出一种天气预报发布服务形式变革的观点，希望能够引起更多地讨论并带来变革的行动。

1 公众对电视天气预报评估的事例

2008年美国《纽约时报》在线讨论中，有一位名叫爱哥斯顿的电气工程师，为帮助在读五年级女儿完成学校气象观测作业，花了7个月时间对当地的电视天气预报节目进行了跟踪评估，其结果值得我们气象工作者思考。通过如下对评估结果的分析，探讨一下我们变革预报发布形式的必要性。这儿要说明一点，就是本节中的观点看法是指公众对我们气象预报的评价。所以有些用语可能过激而不一定反映气象科学的实际情况(这会在第2节中作出进一步分析)。

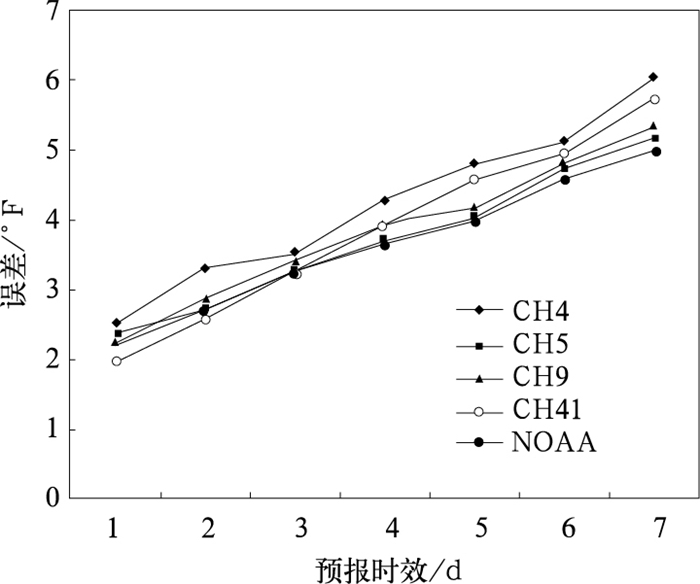
爱哥斯顿从2007年4月20日至11月21日对美国堪萨斯市的4个电视台(4，5，9和41频道)的天气预报节目和美国国家海洋大气局(NOAA)的7天气温和降水统计概率预报进行了为期7个月(共220天)的跟踪比较。电视预报取自晚间10时的预报节目，NOAA的预报取自该局的网页。如果某电视台没有明确给出降水概率，则从预报员的用词、语气和所示的图表来推得。实况用的是堪萨斯市国际机场的观测资料(该市的官方标准记录)来对所有7天的气温和降水概率预报准确率进行评估。比较结果非常有启发意义。当地电视台的预报员和电视台的主管们对此结果的评论也同样令人深思。譬如他们如此说：“我们其实对3天以后的天气一无所知”；“电视台雇用天气预报员时并不考查他们预报的准确率，而更注重他们在镜头前的表达和表演才能”；“其实观众关心的往往只是第二天的天气，所以3天以后天气预报的准确性观众并不太在乎。”当所有4个电视台的首席预报员们被问及“你认为你们最高气温预报应同实际观测值有多接近时，你的预报就算报得很好了？”的问题时，他们一致回答说“3度(华氏)之内”。图 1所示的是1~7天温度预报的绝对误差。可见所有4个电视台和NOAA的一天预报都达到了“3度之内”的标准。对于第二天的预报，除了4频道以外，其他台和NOAA也都达标。但是3天或以上的预报，没有一家达标。随着预报天数的增加，误差几乎呈线性增大。这一不太令人满意的结果，让人看到各家3天或以上的温度预报水平都差不多并都没有达到自定的标准。

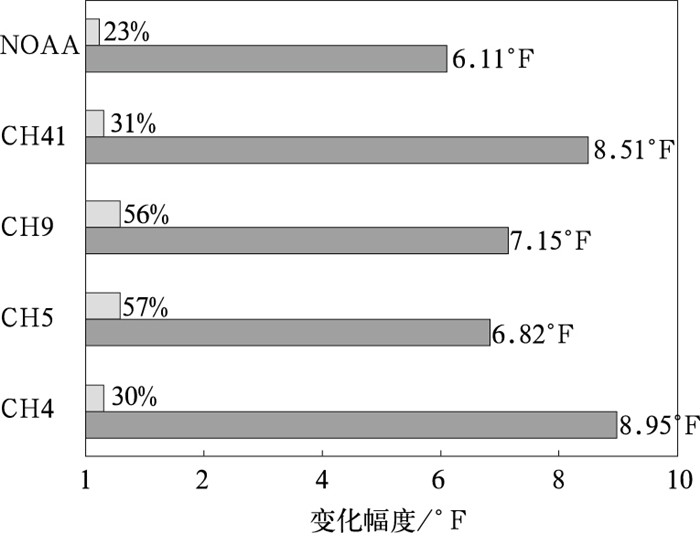
再来看预报的持续一致性问题。譬如针对6月13日这一日做出预报。那么6月6日起报的为7天预报，7日起报的为6天预报，再后就是5天预报等等依此类推直到12日起报的为1天预报。实际上对这同一天的天气，其预报结论天天都在变化(即所谓的滚动订正)，有时这种变化还很大。图 2所示的是各家对7天内的气温和降水概率预报订正的平均变化幅度，变化幅度越小，说明预报的持续一致性越好。从平均来看，NOAA预报的持续一致性最好。但即便如此，NOAA在7天之内气温预报的变化修正幅度也达到了6 °F，降水概率变化幅度达到23%。而各电视台预报的不一致性就更大：气温预报变化达到6.8~9 °F，降水概率变化幅度达到30%~57%。这充分表明了随着时间的推延，各家对于他们自己最初的预报完全缺乏信心。最不一致的一个预报事例是，一家电视台在9月30日(星期天)报10月7日的最高气温为53 °F，而7天后他预报84 °F。两者相差31 °F，最后实况为81 °F。另外的一个事例是，电视台最初报10月15日的气温有83 °F，而2天后改报为53 °F。15日的实测值为64 °F。

这些预报不一致的事例使爱哥斯顿相信21世纪的气象科学还没有发达到可以准确预报未来一周天气的能力。所以，在公众或气象用户看来，气象学家们只能先盲目地将未来7天的最高气温和降水预报的概率猜测出来，而后随着时间的逼近，不断地对预报进行订正。这正如上面提及的来自电视台气象员的坦承：“我们其实对3天以后的天气一无所知”。

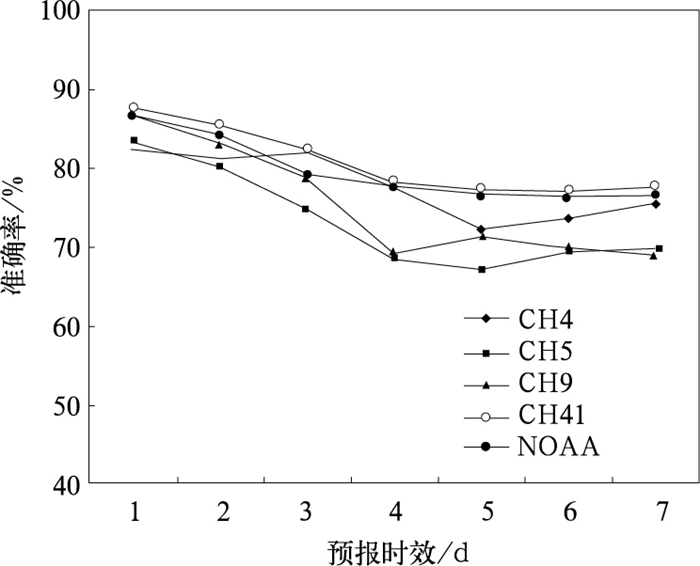
下面再来检验降水预报。通常总是可以假定“天不会下雨”为没有预报的预报，因此，能够获得一点“会下雨”的信息就显得十分重要了。为了定量评估降水预报的准确率，这儿假定预报的降水概率大于50%时，就算“下雨”；反之，就算预报“不下雨”。然后，把这一预报同实况相比较。因为小于0.1 in(相当于2.5 mm)的降水对人的活动没有什么影响，所以“实测有降水”定义为“等于或大于0.1 in”。图 3所示的是根据以上标准所统计出来的各家降水预报的准确率，因为是对逐日的预报与实况的比较，故称为“无条件”预报准确率。第一天的准确率平均为85%，到第7天降至为大约75%，其中41频道和NOAA表现最佳——从87%降至77%。从表面来看，这一成绩似乎并不坏。但是你要知道“如果预报员总是报不下雨的话，从气候角度上讲也会有86.3%的机会正确”。那么如果公众想要得到比仅仅假定“不会下雨”更加确定的信息，一个成功的预报员其降水的预报准确率必须高于86.3%。根据这一标准，只有3家(41频道、9频道和NOAA)的一天预报才算成功。除此之外，所有的预报都比不上“仅仅假定不下雨”的预报。

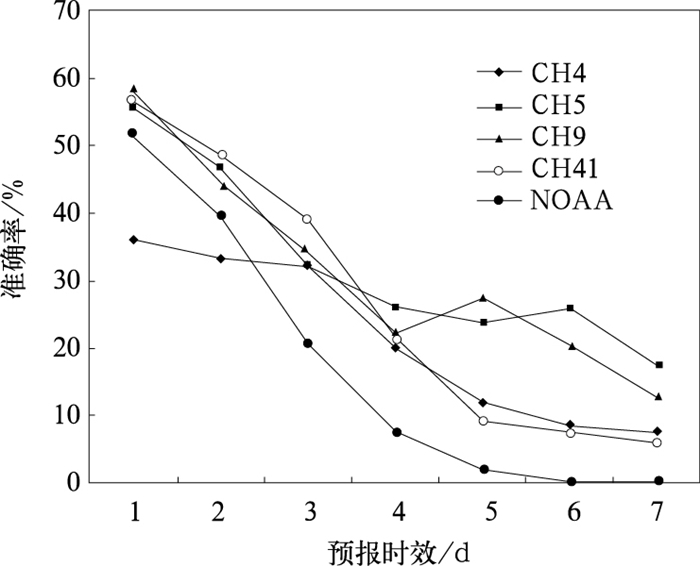
图 3的结果是根据所有的天数统计出来的。但是在夏季有很多时候不会下雨是很明显的。所以在这种时候，预报不下雨对预报员并没有什么挑战意味。因此，度量降水预报的准确率时，最好应该把这些明显不会下雨的天数去掉，称之为“条件”预报准确率。所以在下面的统计中，只包括那些或者预报有降水，或者实况出现降水的天数。这样就把那些明显不下雨的情况去掉，结果如图 4所示。考虑到这样被选择的时段中降水的可能性较大并且较难预报，所以把成功的标准从86.3%降至50%。可惜，除了4家的第一天预报达到此标准外，其他所有的预报都没能达到50%的准确率。换言之，关于2天以上的降水预报，观众还不如用投掷硬币的方法来预测某一天是否会下雨来得更准确些。奇怪的是，在其他评比中一向表现较佳的NOAA，在图 4的评比中却沦为最差(这在3~7天预报中更是如此)。当问及NOAA的气象专家为何会出现这种情况时，得到的回答是：“我们的预报一般比电视台的更加保守一些。只有当我们比较有把握时，才会把降水概率提高到50%以上。”这一回答以及上面的统计结果都使爱哥斯顿相信一件事。就是今天的气象学家虽然有许多资料和工具，但是对于3天以上的天气还是没有相当的把握做出较准确的预报。

既然事实如此，为什么电视台还是要给出3天以上(直到7天)的预报呢？爱哥斯顿认为其原因有二：一是出于商业竞争动机，各个电视台都在这样做；二是他们认为一般公众不会知道他们的预报到底有多准确。所以，这项来自公众对预报评估的结论是呼吁不要试图做超过3天的预报并要求电视台对其自身的预报进行评估。同时，该项评估还提出了改进电视天气预报节目的建议。指出，当有重大天气如洪水、龙卷风、冰雪发生时，电视台的报道、分析非常出色，电视台的主管们也往往牺牲其他正常的节目来让天气预报员有足够的时间来报道这些重大天气事件，深受观众的欢迎。但问题是出在没有什么重大事件发生的平静天气时段，天气预报节目太平淡无味。因此，建议在平静天气的日子里，天气预报节目应被大大地浓缩甚至被取代为用字幕的形式播放，而不应该用“高空低涡”之类的术语来浪费时间。

他山之石可以攻玉。以上事例虽发生在美国，但它仍不失其代表性。因为我们知道类似批评在中国也不少见。譬如有的地方老百姓甚至用打油诗来嘲讽当地的气象台站，如“×××气象站，站长×××；下雨下雪瞎猜猜”。甚至有称气象站为“说谎站”的。更有人打趣说他们很想以预报天气成为他们的职业，因为这样说错了也不会被解雇。如此等等。可见一部分公众对天气预报不准确的抱怨是很常见的现象。那么，为什么这种指责如此普遍呢？我们有没有可能在现有的预报水平上尽量来避免这些指责并为公众提供更好的气象服务呢？

2 公众天气预报发布形式的变革

上述公众自发评估天气预报能力的事例反映了公众对现有预报能力的看法和对准确的天气预报的期望。公众希望天气预报能100%的准确，却发现现有预报往往不如意，有时对，有时错。为什么会出现这种情况呢？其实主要的一个问题是我们现有的确定性的天气预报发布形式传递给公众一种错觉，以为天气可以被完全准确地预报出来。这包括二个方面。一是我们忽略了大气的可预报性问题，使公众从根本上误解了我们预报的真正含义，二是预报的评估及如何让公众理解和认识问题。

为什么我们的预报不准确？气象学家自己通常给出的解释是，大气科学本身还不够完善和精确。这当然有一定的道理，但还不是问题的全部。气象科学确实还需要大大地向前发展，但是否意味着我们有朝一日能够100%准确地预报未来的天气变化？美国著名气象学家洛伦兹早在20世纪60年代就指出大气系统是一个混沌系统，其预测有一个可预报性期限和不确定度^[2]。也就是说初始时刻很小很小一点点的误差，有时会在大气系统中随着时间迅速增长。这使得原本几乎一样的两个预报，随着时间而迅速地变得不相关而失去其可预报性。而这些微的误差在实际的数值预报实践中是完全不可避免的，如观测和模式误差等^[6]。这一伟大的发现告诉我们，完全准确地预报未来天气的变化在科学上是不可能的。既然预报中的不确定性是天气预报的固有属性，我们就应该实事求是地在所发布的预报上把这种不确定性定量地表达出来并事先告知公众，而不应该剥夺他们的知情权只把我们自己也没有十分把握的最佳“猜测”作为唯一正确的预报发布出来。这种没有把预报不确定性定量化的预报是片面的、不完全的、也是不科学的^[5]。更严重的后果是所有用户都只能被迫接受同一个预报结果(值)来做决策, 并因此受到了许多本可避免的损失，同时，也使天气预报受到很多指责。可见，由于我们确定性预报的过份自信，使公众对我们所发布的预报失去了信心。

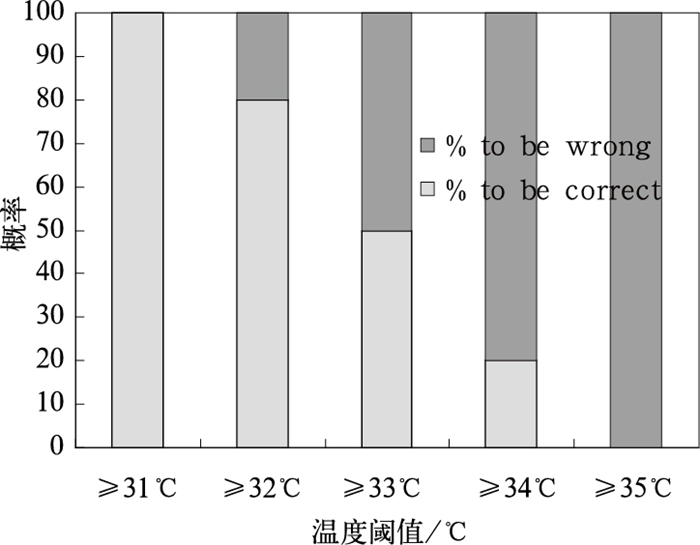
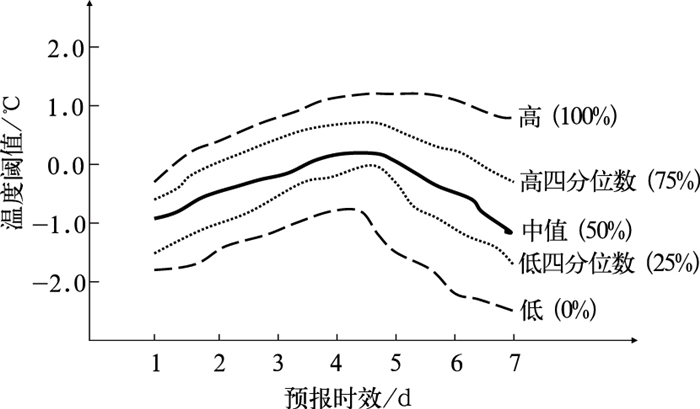
因此，在天气预报的发布形式上，我们需要改变目前“单一确定预报”的做法，诚实地把预报所具有的不确定性定量地告诉公众和用户，以便他们能够根据自身对气象条件的依赖程度来选择他们“自己的”最佳决策结果(值)。图 5是某地某天最高气温(a)和降水预报(b)的一个示范图例, 它分别表征了不同的地面最高温度阈值出现的概率和降水的概率预报。可见，这种预报的表达将预报的不确定性定量地告诉了用户，具体指出了各种可能性的概率大小以供用户科学决策。如要连续预报数天的天气，图 6的表达方法给出了1~7天最低温度低于某一个阈值的可能性，对于一些特定用户而言，或许是一种更合适的选择。当然这种从单一值预报到多值或概率预报的转变不管从技术层面还是从社会影响层面来讲都不是一件容易的事^[7-11]。这至少会涉及以下几点：(1) 如何定量地估计和有效地表达这种预报的不确定性；(2) 不像单一值预报其对错分明，而对多值或概率预报我们该如何来检验它们的对或错；(3) 作为气象预报的用户该如何用概率来做决策？譬如预报说50%的可能性下雨，50%的可能性不下雨，我们该听哪一个？本文中，爱哥斯顿将50%的概率作为有无降雨的“决策”判别值，只能是公众在有限信息情况下的简单选择。

当公众明白了大气的可预报性问题后，那么对于爱哥斯顿文章中另一个误解(即气象学家对3天以上的预报其实一无所知)也就比较容易向公众说清楚并加以纠正了。显然，我们对于3天以上的天气不是一无所知的。而只是随着预报时间的增长，预报的不确定度(误差)一般也随之增加，即单一确定的预报变得愈来愈不可靠。所以，在没有超过可预报性极限(目前理论上认为二周左右，但随着模式的精细化程度的提高，这个极限也许会变得更长)之前，只要我们定量地给出预报的不确定度，超过3天以上的预报还是有很重要的参考价值，事实上，目前很多的数值预报模式都能相当不错地把风暴气旋提前一个星期预报出来。即使随着预报时间不断延长，具体到某时某地的气象的要素预报已超过其可预报的极限时段而不再可信，但是我们知道它们在时间上或空间上的平均状态却仍然是可预报的，譬如月和季节预报报的就是某月温度和降水的平均状态如偏高(多)或偏低(少)等等。所以关于这一点我们也应该向公众说清楚。当然基于同样道理，对于这些平均预报也同样要给出其可能的误差范围或预报的不确定度。

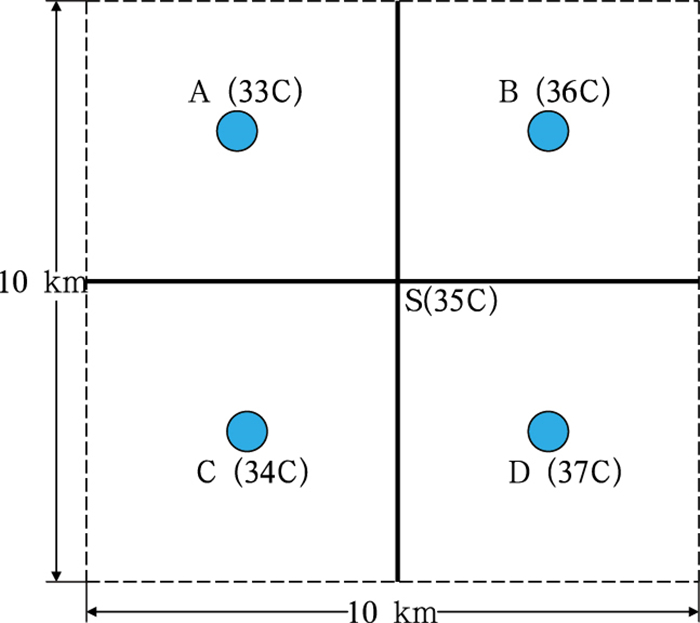
下面再来谈谈预报的精细化和准确率的问题，这往往也是公众认为我们预报不准确的来源之一。随着数值天气预报的准确率和精细程度越来越高，日常的天气要素预报如温度、降水、云和风等都愈来愈依赖于数值模式的直接输出。但模式输出值代表的是一个网格上的平均值，而不是某一点上的值。因计算机条件和数值解法的限制，网格总有一定大小的，因此，预报不可能无限的精细化。如：我们都知道白天一栋房子的背阳面气温往往会比朝阳面低很多，但是我们现在的温度预报还不可能小到连某一栋房子的朝阳面和背阳面都能分辨出来。图 7表示S这一点的气温数值预报值是35 ℃。假如模式的水平格距是10 km×10 km，那么这个35 ℃的预报值就是这一范围内的平均气温。现在该区域内有4个地点A、B、C、D实测的气温分别为33 ℃、36 ℃、34 ℃和37 ℃。这样对于A和C两地的人来说，35 ℃报得太高了，而对B和D两地的居民而言，35 ℃又太低了。结果，所有4方居民都认为我们的预报是不准确的，但实际上从数值模式角度来说这一预报是完全准确的，因为A、B、C、D 4地(假定观测可以代表该点附近的基本情况)的平均温度正好35 ℃。所以，我们要把我们预报值所代表的真正意思和同某一特定观测点所看到实况之间的可能差异要通过科普宣传的方法告诉公众。让他们不至于把预报值误解为某一特定点上的观测值。这对于降水、风、温度和云等要素的预报都是如此。

总之，对于预报的不确定性问题、不同预报时效有不同预报对象的问题以及预报如何正确检验的问题。这些都要广泛地进行科普宣传，要把它们写到中小学和大学的有关公共教材中去。让所有的人包括一般公众、决策者和气象专业用户都非常明确地明白这些科学事实，以便他们不至于盲目地向气象部门提出不切实际的、不科学的要求和不着边际的指责。同时，对于气象专业用户，气象学家应该同他们进行具体的合作，并针对他们的气象风险承受程度来制定行业气象决策模式。其实，当人们认识到了天气预报的不确定性本质，并科学地把这一不确定度定量地考虑在他们的决策过程中，他们就会把风险降到最低，而获利最大。这正是我们气象工作者最愿意看到的结果^[10]。所以现在是我们该考虑改变天气预报的发布和服务形式的时候了，将预报的不确定性作为预报发布的一部分表达出来。

致谢：本文在写作过程中得到中国气象局矫梅燕同志的大力帮助和指点，特此致谢！