2. 武汉大学水资源与水电工程国家重点实验室,武汉 430072
2. State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072
雷达估测降雨的研究自20世纪40年代末开始,但其在水文学中的实际应用起步较晚,始于20世纪70年代。在这期间,水文学家利用雷达测雨技术进行水文学的研究,并取得了一些重要的成就[1-5]。未来水文科学的发展在很大程度上取决于水文数据的获得及其精度,降雨的时间和空间分布具有很大的不确定性,但是降雨是水文预报最重要的输入信息,测雨雷达可随时跟踪雨区范围、暴雨走向和降雨量的变化,测得高时空分辨率的降雨。数字化的雷达降雨、地理信息系统以及数字高程图的获得,推动了新一代分布式降雨-径流模型的开发,并将极大地拓宽水文学研究的思路和方法,加大水文学研究的广度和深度。因此,在雷达测雨技术的支持下,水文预报的发展将会进入一个崭新的阶段。为此本文以湖北省白莲河流域为例探讨雷达定量测雨技术在流域汛期短期洪水预报中的应用。
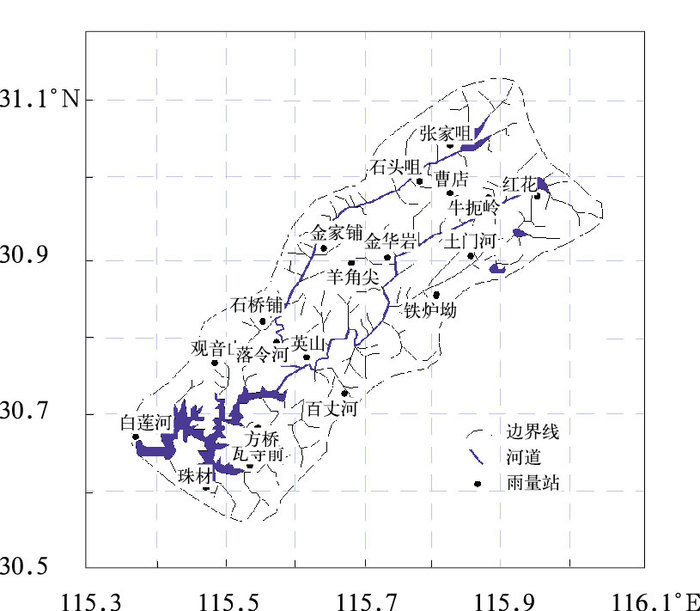
1 流域概况白莲河水库位于湖北省东部浠水河中游,控制流域面积1797 km2,总库容12.28亿m3。浠水河地处长江中游下段,源于大别山,上游分东西两条河流,汇入英山县城以下2 km处的双河口,流经英山、罗田、浠水等县于兰溪镇注入长江。水库流域形状南北长,东西窄,平均宽度为15.7 km,略似芭蕉叶形状。地势东北高,西南低(如图 1所示)。
|
图 1 白莲河流域的示意图 Fig. 1 The sketch map of Bailianhe Catchment |
本流域属鄂东暴雨区,多年平均降雨为1366 mm,雨量时空分布不均,集中在6—8月份,暴雨次数多,强度大,洪水陡涨陡落,汇流时间短。流域内水文监测网分布均匀(见图 1),并且位于武汉雷达监测网之内,有利于短期洪水预报研究的开展。
2 雷达定量测量降水的方法雷达定量测量降水的方法有多种,最常用的是Z-I关系法,即应用雷达气象方程由测得的降水回波的反射率因子,然后根据反射率因子和降水强度之间的关系来推算降水强度。
由雷达反射因子Z和降水强度I的定义可知,目前我们在合理的假设基础上,从理论上探讨Z-I关系。目前常用的雷达估算降雨一般表达式如下:
Z=AIb
在实际情况中一次降雨过程中,降水实际上是不均匀的,且随时间变化;雨滴谱也随时间、空间和不同降水类型而变[6-8]。所以一般在实际雷达定量测量降水中,除参考上述的理论关系外,都根据当时当地的实际情况,应用实测的滴谱资料,具体统计Z-I关系中的系数A和b值,为此本文结合实际资料采用分组Z-I关系来探讨雷达定量测雨的方法。
2.1 分组Z-I关系测量降水的原理多年来很多人在不同地点用实测的滴谱资料统计Z-I关系,结果表明,其系数A和b值的变化范围很大。例如在降雨过程中A从16变化到1200,b值从1变化到2.87。可见Z-I关系不是固定的,它不仅随地点、季节以及不同降水类型而变,即使在同一次降水过程中,其A和b值也是变化的。Z-I关系的不稳定性,给雷达定量测量降水带来了某种困难,有些人对大量的雷达资料进行分析,按降水成因、气候特征或天气系统特征分别对不同类型降水统计出相应的Z-I关系。虽然这些分类法都比较复杂,且不易操作对Z值分组求取Z-I关系,但用计算机处理都是简单易行的。
用雨量计测得每小时雨量Gi,同时由雷达测得时空相对应的Z值,事先假定一个Z-I关系式:
| $Z=A{{I}^{b}}$ | (1) |
也就是假定上式中A和b的值,把Z转换成雨强,再对雨强进行时间积累得到雷达估算的每小时雨量Hi,选取判别函数为:
| $GTF=\min {{({{H}_{i}}-{{G}_{i}})}^{2}}$ | (2) |
式中,i为样本的序号,是不同时间的取样值,N是样本总数。不断调整A和b的值,使CTF为最小。使CTF为最小的A和b就是这个统计样本总体的最优参数。
2.2 资料选取及优选结果根据流域资料收集情况,选取资料包括2004年汛期6分钟一次的雷达基数据资料以及白莲河流域2004年19个雨量站时间间隔为1小时实测的降雨资料和水库水位资料。
在实际估算过程中,采用常用的复合平面技术处理雷达回波,具体做法如下:15 km以内用第四层数据,15~40 km取第三层数据,40 km以外取值由第一、二层数据视第一层遮挡情况或是否存在超折射而定:第一层被完全遮挡的区域取第二层数据,否则根据上下层回波强度与回波面积乘积之和的比值大小决定取第二层数据或者取两者之间的大值。
根据实际资料情况按照Z值大小把12630个样本分为四组,即Z<20, 20≤Z<30, 30≤Z<40, Z≥40,分别用最优化处理方法得出Z-I关系。优选过程中,我们设定A参数从10到400,步长为10;b参数从0.5到4.5,步长为0.1,分析CTF场。对应于每一个A和b值,就得到一个CTF值,不断地改变A和b的值,就得到CTF随A, b的两维分布,即CTF场。CTF最小值所对应的A和b就是要求的最优化参数,也就得到了最优化的Z-I关系,见表 1。
|
|
表 1 A,b优选参数表 Table 1 The optimal parameters of A and b |
利用上述的Z-I关系将雷达反射率转化为降雨,和由典型的Z=200I1.69公式计算的降雨分别做比较,分析使用哪种方法转化的降雨最接近雨量站实测值(结果见表 2)。鉴于雷达的测量结果受到多方面干扰因素的影响, 使得雷达测值存在着相当大的误差。本文在研究过程中结合流域雨量站实时监测资料采用卡尔曼滤波方法对利用分组Z-I关系估算得到的雨量进行校准(见表 2)。
|
|
表 2 雨量估算结果比较(单位:mm) Table 2 The comparison of precipitation estimation results (unit: mm) |
根据试验流域湿润的气候特点,本文选择在国内外水文预报工作中得到较好应用的新安江模型作为流域水文预报模型[9-13]。该模型应用了蓄满产流与马斯京根汇流概念, 有分单元、分水源、分汇流阶段的特点, 结构简单, 参数较少, 各参数具有明确的物理意义, 计算精度较高。模型通过把全流域分成多个单元流域, 在每一个单元流域内, 降水经过蒸散发的消耗后, 以蓄满产流的方式经产流量水源划分后对各单元流域进行产汇流计算, 得出单元流域的出口流量过程;再进行出口以下的河道洪水演算, 把各个单元流域的出流过程相加, 就求得了流域的总出流过程。
3.2 洪水预报结果评定指标汇流预报方案采用模型的有效性和洪峰流量场次合格率及峰现时差指标来评定。
(1) 模型有效性评定
对有效性评定采用确定性系数DQj:
| $D{{Q}_{j}}=1-\frac{{{S}^{2}}}{{{\sigma }^{2}}}$ |
其中:
| $\begin{align} & S=\sqrt{\frac{\sum\limits_{i=1}^{M}{{}}{{(Q{{\prime }_{i}}-\bar{Q}\prime )}^{2}}}{M}}\begin{matrix} {} & \sigma =\sqrt{\frac{\sum\limits_{i=1}^{M}{{}}{{({{Q}_{i}}-\bar{Q})}^{2}}}{M}} \\ \end{matrix} \\ & \quad \quad \quad \quad D{{Q}_{SA}}=\frac{1}{N}\sum\limits_{j=1}^{N}{{}}D{{Q}_{j}} \\ \end{align}$ |
式中DQSA为汇流方案总场次洪水流量过程平均确定性系数;DQj为场次洪水流量过程确定性系数;S为场次洪水流量过程预报误差的均方差,其中的Q′i为场次洪水流量预报值, Q′为预报场次洪水流量均值;σ为场次洪水流量过程的均方差;其中的Qi为场次洪水流量实测值;Q为实测场次洪水流量均值;M为场洪水流量过程总节点数;N为洪水场次总数。
(2) 洪峰合格率
| $D{{Q}_{m}}={{N}_{合格}}/N\times 100\%$ |
式中DQm为预报洪峰流量合格率;N合格为模拟洪峰流量小于等于实测洪峰流量的相对误差20%的合格洪水场次数。
(3) 峰现时差
| $DT=\sum (\left| {{T}_{Q计}}-{{T}_{Q实}} \right|\le 3)\text{ }/N$ |
式中DT为峰现时间小于等于3个时段长的洪峰次数与洪峰总次数的比值;TQ计为预报洪峰流量峰现时间;TQ实为实测洪峰流量峰现时间。
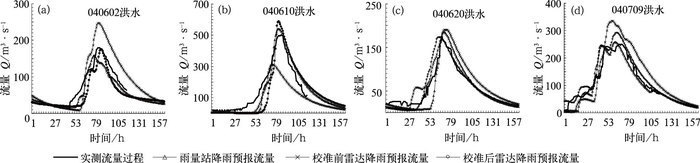
3.3 模拟试验方案与结果为了进一步确定雷达估算降雨量对洪水预报结果的影响,分别将雨量站监测降雨量、校准前雷达估算降雨量、校准后雷达降雨估算降雨量输入新安江水文模型对白莲河流域2004年汛期4场(分别为2004年6月2日、6月10日、6月20日和7月9日。表示为040602、040610、040620和040709,下同)洪水进行了模拟试验,模拟流量过程与实测流量过程的对比如图 2所示。
|
图 2 模拟试验流量过程线对比 Fig. 2 The contrast analysis of flow processes in simulation test in 2004 |
对实测雨量站降雨的模拟结果做出有效性的评定, 结果见表 3。洪水流量过程平均确定性系数为84.55%。模拟洪峰流量合格率为100%。峰现时差≤3个时段百分率=50%。
|
|
表 3 雨量站观测降雨形成的洪水流量过程模拟结果 Table 3 The flood simulation results based on rain gauge data in 2004 |
对未经过卡尔曼滤波订正雷达降雨的模拟结果做出有效性的评定,结果见表 4。洪水流量过程平均确定性系数为57.725%。模拟洪峰流量合格率为25%。峰现时差≤3个时段百分率=25%。
|
|
表 4 未校准的雷达观测降雨形成的洪水流量过程模拟结果 Table 4 The flood simulation results based on radar data without check in 2004 |
对经过卡尔曼滤波订正的雷达降雨模拟结果做出有效性的评定,结果见表 5。洪水流量过程平均确定性系数为80.775%。模拟洪峰流量合格率为100%。峰现时差≤3个时段百分率=100%。
|
|
表 5 校准后雷达观测降雨形成的洪水流量过程模拟结果 Table 5 The flood simulation results based on radar data with check in 2004 |
由上述结果(表 3,4,5) 可以看出,未校准雷达估算降雨量直接输入水文模型,其结果是不理想的,但校准后的雷达降雨的洪水模拟精度要比校准前的要高很多;另外由于雷达在探测降雨时间和空间上的敏感性,校准后的雷达降雨的洪水预报的峰现时差要比用雨量站观测降雨的预报要小,但由于雷达估算降雨Z-I关系的不确定性以及其他人为因素的影响,降水估算资料与实际存在一定的差异,使得用校正后雷达降雨的洪水预报的洪水过程效率系数并不优于用雨量站测得的降雨做出的预报。综合平均确定性系数、预报洪峰流量合格率、峰现时差≤3个时段百分率三个评价指标,可以看出使用校准后的雷达降雨结果作为水文模型的输入总体洪水模拟水平是最优的。
3.4 预报试验与结果为了进一步验证模拟试验的实用性,按照模拟试验方案分别将雨量站监测降雨量、校准前雷达估算降雨量、校准后雷达降雨估算降雨量输入新安江水文模型对白莲河流域2006、2007年汛期4场洪水(分别为2006年5月8日,7月5日以及2007年6月27日,7月1日。表示为060508、060705、070627和070701,下同)进行了洪水预报试验,预报试验流量过程与实测流量过程的对比如图 3所示,并对预报试验结果进行了评定,见表 6~8。

|
图 3 预报试验流量过程线对比 Fig. 3 The contrast analysis of flow processes in forecast test in 2006-2007 |
|
|
表 6 雨量站观测降雨形成的洪水流量过程模拟结果 Table 6 The flood simulation results based on rain gauge data in 2006-2007 |
|
|
表 7 未校准的雷达观测降雨形成的洪水流量过程模拟结果 Table 7 The flood simulation results based on radar data without check in 2006-2007 |
|
|
表 8 校准后雷达观测降雨形成的洪水流量过程模拟结果 Table 8 The flood simulation results based on radar data with check in 2006-2007 |
对实测雨量站降雨的预报试验结果评定如下(表 6):洪水流量过程平均确定性系数为85.125%。预报试验洪峰流量合格率为100%。峰现时差≤3个时段百分率=75%。
对未经过校正雷达降雨的预报试验结果评定如下(表 7):洪水流量过程平均确定性系数为50.325%。预报试验洪峰流量合格率为0.0%。峰现时差≤3个时段百分率=25%。
对经过校正的雷达降雨的预报试验结果评定如下(表 8):洪水流量过程平均确定性系数为82.55%。预报试验洪峰流量合格率为100%。峰现时差≤3个时段百分率=100%。
由上述结果(表 6,7,8)可以看出,预报试验结果与模拟试验结果基本一致,未校准雷达估算降雨量直接输入水文模型,其预报结果依然不理想,校准后的雷达降雨结果作为水文模型的输入总体洪水预报水平仍是最优的。
4 结论降雨量是洪水预报中最重要的信息之一,同时又是径流模拟中最大的不确定因素之一,降雨不仅是所有水文过程的驱动力,降雨的时空变化还影响径流总量、洪峰流量,洪峰出现的时间,因此在水文模型中降雨的精确测量和准确描述是定量水文分析的基础。洪水预报的精度, 通常可以通过不断改进洪水预报模型和资料获取的手段来提高。本文从水文模型资料获取手段的角度,以湖北省白莲河流域2004年汛期4次洪水过程为例,通过雷达测雨技术获得时间和空间上高分辨率的降雨信息,作为水文模型的输入,用作模拟试验,在此基础上用2006、2007年汛期的4次洪水过程作了预报试验。其结论如下:
(1) 结合当地实际情况,利用分组Z-I关系得到的降雨,比没有分组以及典型的Z-I关系转化的降雨与雨量站实测的降雨在水量上更加接近。
(2) 利用卡尔曼滤波校正后的降雨比没有校正的雷达降雨在水量上更加接近雨量站实测的降雨。
(3) 从雷达测量降雨和雨量站实测降雨用于洪水预报的结果可以看出,未校准雷达估算降雨量直接输入水文模型,其结果是不理想的,但校准后的雷达降雨的洪水预报精度要比校准前的要高很多。另外由于雷达在探测降雨时间和空间上的敏感性,校准后的雷达降雨的洪水预报的峰现时差要比用雨量站观测降雨的预报要小;但由于雷达估算降雨Z-I关系的不确定性以及其他人为因素的影响,使得用校正后雷达降雨的洪水预报的洪水过程效率系数并不优于用雨量站测得的降雨做出的预报。总体上来看使用校准后的雷达降雨结果作为水文模型的输入总体洪水预报水平是最优的。
(4) 研究表明雷达定量估算降雨技术凭借其特有的技术优势,其作为水文模型中获得降雨量时空分布的手段有助于洪水预报精度的提高,进一步推动水文预报的发展,但有待进一步提高,以期寻求更好的方法解决雷达测雨信息进行水文应用的难题,使雷达测雨技术在水文学的应用中发挥应有的作用。
刘晓阳, 毛节泰, 李纪人, 等, 2002. 雷达估测降水模拟史灌河流域径流[J]. 北京大学学报(自然科学版), 38(3): 342-349. |
杨扬, 张建云, 戚建国, 等, 2000. 雷达测雨及其在水文中应用的回顾与展望[J]. 水科学进展, 11(5): 92-98. |
刘金涛, 李致家, 2004. 基于雷达测雨的实时洪水预报模型[J]. 河海大学学报(自然科学版), 3(5): 488-491. |
Liu Xiaoyang, Mao Jietai, 2003. Runoff simulation using radar and rain gauge data[J]. Adv Atmos Sci, 20(2): 213-218. DOI:10.1007/s00376-003-0006-7 |
张亚萍, 周国兵, 胡春梅, 等, 2008. TOPMODEL模型在重庆市开县温泉小流域径流模拟中的应用研究[J]. 气象, 34(9): 34-39. DOI:10.7519/j.issn.1000-0526.2008.09.005 |
王建林, 刘黎平, 曹俊武, 等, 2005. 双线偏振多普勒雷达估算降水方法的比较研究[J]. 气象, 31(8): 5-10. |
王治平, 张中波, 唐林, 等, 2009. 应用多普勒雷达回波参数对长沙地面降水的估算[J]. 气象, 35(8): 104-108. DOI:10.7519/j.issn.1000-0526.2009.08.013 |
刘娟, 宋子忠, 刘东风, 等, 1999. 分组Z-I关系及其在淮河流域雷达测雨中的应用[J]. 气象科学, 19(2): 213-220. |
赵人俊, 1984. 流域水文模拟[M]. 北京: 水利电力出版社.
|
赵人俊, 王佩兰, 1988. 新安江模型参数的分析[J]. 水文, 8(6): 2-9. |
Zhao R J, 1992. The Xinanjiang model applied in China[J]. Journal of Hydro logy, 135: 371-381. |
朱求安, 张万昌, 2004. 新安江模型在汉江江口流域的应用及适应性分析[J]. 水资源与水工程学报, 15(3): 19-23. |
李允军, 宋星原, 2005. 淮安市龙王山水库流域洪水预报研究及应用[J]. 三峡大学学报(自然科学版), 27(3): 209-212. |
 2010, Vol. 36
2010, Vol. 36 