当前,对可再生能源的开发利用得到了前所未有的重视。风能作为一种主要的可再生能源,亦得到了足够的重视。在国家发改委和中国气象局的指导下,各省普遍开展了相关区域的风能资源的调查评估和开发利用工作。
在该项工作中,风速随高度垂直分布特征对于风电场的风能评估具有重要意义[1-2],同时,风速的这种分布对于风电场风机的正常安全运行也有重要意义。近地层风的垂直分布主要取决于地表粗糙度和低层大气的层结状态。同时,由于风力机制造技术不断提高,单机功率逐渐增大,风轮直径也相应地增大,风能利用高度有向高发展的趋势。因此,研究风速随高度的变化规律及风能特征值随高度的变化规律是风能利用中十分重要的问题。
目前,对风速垂直切变的研究应用大多局限于大气污染的控制方面,赵鸣等[3]利用天津塔层观测资料研究了风切变随高度的变化规律及其影响因子,同时,城市建筑群地表植被条件对风切变的影响也取得了若干成果[4-5]。而针对风电场建设运行的风速垂直切变特征的研究还较少。湖北省位于我国中部,境内包括丘陵岗地、山区、平原等多种地形,湖北省风能资源普查揭示出湖北省风能资源丰富区域主要集中在山体相对孤立的中高山区、北部及汉江中游的主要风口以及大型湖泊的周边地区等具有特殊地形地貌的区域,这些地形之间的地表粗糙度差异较大。本文利用三种不同地形条件下70 m高度测风塔1年完整的观测数据,研究了不同地形条件下风速随高度的变化特征。该研究能够为湖北省的区域风能资源评估和风电场的正常运行提供科学的参考依据,对加强风能资源的开发利用具有实际意义。
1 资料 1.1 资料选取及处理根据风能普查的结果,湖北省风能资源较为丰富的地区主要集中在山区丘陵,受地形影响较大。因此,分别选取钟祥华山观、大悟仙居顶和黄冈龙感湖代表丘陵岗地、山区和水体三种不同下垫面,其中龙感湖测风塔位于湖边大堤上。采用三处70 m测风塔的1年观测数据,其中华山观的资料时间为2006年10月至2007年9月,仙居顶和龙感湖资料时间均为2006年4月至2007年3月,各测风塔的具体情况见表 1。
|
|
表 1 梯度测风塔基本情况 Table 1 The situation of wind tower |
依据《风电场风能资源评估方法》(GB/T 18710-2002),分别对三个70 m测风塔的原始数据进行合理性检验,除此之外,对于梯度观测站,各观测层次数据的一致性、合理性进行判断;对同时段各测风站观测数据的一致性、合理性进行判断;并且对重大天气过程,如强冷空气、热带气旋等天气条件下风速的合理性进行判断。
1.2 计算方法风切变指数是表征风速垂直变化的主要特征量之一。风切变是指在大气边界层中,由于受地球表面的作用,平均风速随高度变化的现象[6]。目前,对风速切变指数的计算用得较多的方法主要是对数律和指数律[7-8]。我国新修订的《建筑结构设计规范》推荐使用幂指数公式,其表达式为:
| $u={{u}_{1}}{{(\frac{z}{{{z}_{1}}})}^{\alpha }}$ | (1) |
式中:u为z高度处的风速, u1为z1高度处的风速, α为风速高度变化幂指数,其值的大小即表明了风速垂直切变的强度。
对上式作变换并等号两边取对数,即得:
| $\rm{ln}(\frac{\mathit{u}}{{{\mathit{u}}_{1}}})=\alpha \rm{ln}(\frac{\mathit{z}}{{{\mathit{z}}_{1}}})$ | (2) |
令
则得到线性方程y=αx。将实测的资料序列代入上式,得到序列y1,y2,…, yi, …, yn;x1,x2,…, xi, …, xn,用最小二乘法拟合回归系数,得到指数α的计算公式:
| $\alpha =\sum {{\overline{\mathit{x}}}_{\mathit{i}}}{{\overline{\mathit{y}}}_{\mathit{i}}}/\sum \mathit{x}_{\mathit{i}}^{2}$ | (3) |
10~30 m、30~50 m、50~70 m各层的切变指数用公式(1) 直接计算,10~70 m、10~50 m和30~70 m间的切变指数使用公式(3) 计算。
2 风速随高度的变化特征 2.1 风速随高度变化的差异大气边界层的风场分布除受大型天气系统的影响外,更受地形作用、下垫面性质不同引起的热力作用等影响,是三种因素共同作用的结果,使风场具有独特的垂直、水平结构,并有明显的时间变化[9]。
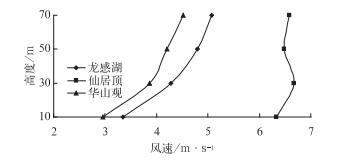
图 1为三个测风塔处年平均风速随高度的变化曲线。从图 1中可以看出,龙感湖和华山观处风速随高度的变化较为一致,为明显的增大趋势,仙居顶在30 m至50 m高度,风速出现下降。根据文献[10]可知,气流流过山体时流场将形成一个回流区,若风速较大或大气层结不稳定,则在山体背风面会出现强烈的涡旋运动,这种涡旋运动可能会导致风速在某一高度出现回转风速,从而表现出风速随高度而减小的现象。这可能是导致大悟仙居顶在30 m至50 m高度之间出现下降的原因之一。
|
图 1 不同测风塔各层高度的风速垂直变化曲线 Fig. 1 The curves of wind speed change with height for different wind tower |
表 2为三座测风塔各高度实测风切变指数。根据10~30 m、30~50 m和50~70 m各层的切变指数可以发现,随着高度的增加,龙感湖和仙居顶的各层切变指数表现出先增加后减小,而华山观有着相反的趋势,为先减少再增加。由于大气层结对风的影响愈向上愈大[3],且近地层平均风廓线的统计特征主要反映的是下垫面的作用[4]。仙居顶处的风速垂直切变指数与龙感湖和华山观相比,明显较小,因此,该处下垫面对风速的垂直变化的影响较小,而其他两处受下垫面的影响较大。
|
|
表 2 各测风塔实测风切变指数 Table 2 Wind shear index of different towers |
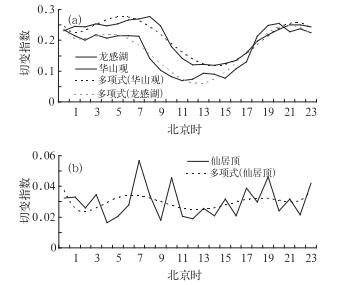
图 2为不同地形条件下风速垂直切变的日变化。从多项式拟合曲线可以看出,龙感湖、仙居顶和华山观风速垂直切变指数的日变化趋势相似,均为接近正弦波形,尤其是龙感湖和华山观。而仙居顶测风塔位于孤立的山顶上,受下垫面作用影响较小,导致其风速垂直切变指数较小,趋势不是很明显;同时,该处切变指数表现出波动频繁的特性,说明该处影响风切变指数的因素更为复杂。
|
图 2 不同地形下垂直切变指数日变化 (a)龙感湖和华山观,(b)仙居顶 Fig. 2 The diurnal variations of vertical shear index under different terrain conditions at (a) Longganhu and Huashanguan, and (b) Xianjuding |
从总体上来看,不同地形下切变指数的变化均表现出白天较小,夜间较大的特征。这是由于从中午到傍晚大气层结处于不稳定或中性状态,大气湍流混合作用更加明显,从而导致上下层间动量交换频繁,风速垂直梯度较小,而夜间温度层结稳定,湍流弱,动量不易下传,表现出上下层的风速垂直变率大,特别是在丘陵山区,夜间容易出现中低层逆温情况,逆温的上下边界区正处于风速切变区,进一步导致风速垂直切变的增大。
同时,在不同地形条件下,α的峰谷值出现的时间也存在显著的差异性。其中华山观峰值出现在凌晨至上午09时及21时之后,谷值出现在午后,14时左右降至最低;对比华山观的日变化,龙感湖切变指数的“波形”要提前2个小时左右,峰值出现在07时之前和19时以后,谷值出现在12时左右。
仙居顶处海拔为583 m,属于山地地形,周围地形状况复杂,且起伏大。与平原地区相比,山地地形有利于加剧近地层的大气湍流交换作用,导致大气层结更加不稳定[4]。风在吹向测风塔的同时,不断受到起伏地形的影响,且由于仙居顶为孤立山体,地面粗糙度对风速的影响较小,使得其在测风塔处表现出梯度风变化较小,这也许是仙居顶处的风速垂直切变较小以及波动更为频繁的原因之一。
但同时我们也发现华山观地区属于丘陵地区,与龙感湖地区相比,海拔高度相差100多米,按照文献[4]的结论,其风速切变指数应小于龙感湖。但从图 2中可以看出,华山观风速垂直切变指数要普遍要大于龙感湖,因此,与大气层结状况影响相比,不同地形条件下的地面粗糙度是主导影响因素。龙感湖地区地势平坦,周围大都为水体、农田和树木,地面粗糙度相对较小,由此对近地层风速的影响较小,而华山观位于丘陵地区,地形起伏相对较大,周边多为高低不齐的树木和杂草以及裸露的沙石,地表粗糙度大,从而导致风速在上下层表现出更为明显垂直变化。
2.3 风速垂直切变的季节变化图 3、图 4为不同地形条件下风速垂直切变指数的年变化和季节变化情况。

|
图 3 不同地形下风速垂直切变指数的年变化 Fig. 3 The annual variations of vertical wind shear index under different terrain conditions |
|
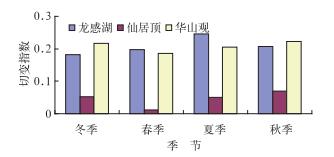
图 4 不同地形条件下风速垂直切变的季节变化 Fig. 4 The seasonal variations of vertical wind shear index under different terrain conditions |
不同下垫面性质对风廓线的影响在冬季的差异更加明显,在夏季稍弱。即在夏季不稳定层结作用加强而下垫面动力减弱[4]。这是因为在不稳定层结占优势的夏季,由于热对流效应的加强,大大减弱了下垫面的动力作用,加上经常发生的中小尺度对流天气系统,造成近地层平均风廓线的统计特征在很大程度上受到局地热力状况的影响,因此统计分析结果反映出的规律也与冬季不同。
如图 4所示,三种地形条件下,切变指数最大值出现时间存在明显的差异,龙感湖切变指数在冬季最小,夏季最大;仙居顶在秋季最大,春季最小;华山观在秋季最大,春季最小。
因此,从实际情况来看,在三种不同地形条件下,切变指数并没有表现出明显的冬春季节偏大,夏秋季节偏小的一般特点,且在不同的地形条件下有不同的特点。这说明在复杂地形条件下,地形和下垫面的粗糙状况始终是影响局地风垂直切变的主导因素。如龙感湖地区切变指数在从1月份开始出现上升,在夏季7月份达到最大,之后出现下降趋势,这可能与周围水体有关。
2.4 不同风速范围的垂直变化差异考察了三种地形下,不同风速段内垂直切变指数的情况。将观测资料的风速分为<6 m·s-1和≥6 m·s-1两种情况进行分析。
根据文献[5]的结论,随着输入风速的增加,风速减小率呈降低趋势,并且风速减小率随输入风速的增加而减小的趋势更加明显。这是由于随着输入风速的增大,地表对于气流的阻挡和削弱作用并没有随之增大,或者没有输入风速增加的程度大,从而表现为地表阻碍作用效果相对减小,导致对风速减小率的影响降低。由此可见,随着输入风速的增大,地表粗糙度的影响在不断降低。从表 3中可以发现,不同地形下在不同风速段内垂直切变指数的变化趋势是一致的,风速较小时要普遍大于风速较大情况,且风速较小情况下比风速较大时高出接近一个量级。这与文献[5]的结论是一致的。
|
|
表 3 不同风速段内垂直切变指数 Table 3 The vertical wind shear index for different wind sections |
比较不同地形条件下,不同风速段内切变指数分布的差异,龙感湖在不同风速段内垂直切变变化最为明显,两者相差0.078;仙居顶由于本身的风速切变较小,在不同风速段内的切变指数的变化也最小,为0.01;华山观相差0.035。
2.5 大风情况下垂直风切变推算风电场设计中最关心大风尤其是极值情况,为此,我们根据各测风塔不同高度上年最大风速随高度变化的相对值序列,利用最小二乘法拟合,得到不同地形条件下大风情况下的风廓线指数(如表 4)。
|
|
表 4 大风情况下垂直切变指数 Table 4 The vertical wind shear index under strong windy conditions |
从表 4中可以看出,龙感湖、仙居顶和华山观在大风情况下的切变指数分别为0.20、0.012、0.152。与一般情况下相比,垂直切变指数均出现明显的减小。
3 讨论为了进一步的验证仙居顶风速随高度的垂直变化的合理性,利用仙居顶另一个70 m塔(31°32′24″N、114°25′15″E,海拔594 m,2#测风塔)2005年12月2日至2006年7月31日的测风数据,计算了其切变指数(如表 5所示)。从表中发现,2#测风塔风速随高度上升而增大,并未出现“倒切变”现象,但与此同时,通过对比不同高度之间风速的垂直切变指数可知,虽然在30~50 m高度风速仍呈增加趋势,垂直切变指数却明显偏小,这说明风速在此高度范围内风速增加速率显著减小。这与仙居顶1#测风塔风速随高度的变化趋势是一致的,也从侧面证明了仙居顶处在离地面30~50 m高度风速受到了一定的扰动。除了上文中提到的原因外,扰动产生的具体原因还需要进一步的深入研究。
|
|
表 5 仙居顶2#测风塔实测风切变指数 Table 5 Wind shear index of No.2 tower at Xianjuding |
利用对黄冈龙感湖、大悟仙居顶和钟祥华山观测风塔观测资料,分析了不同地形条件下,风速垂直分布日变化、年变化特征,得到以下一些结论:
(1) 由于地形和下垫面性质的差异,华山观处风速随高度的变化最大,龙感湖次之,仙居顶处最小;切变指数的变化均表现出白天较小,夜间较大的特征。垂直切变指数的日变曲线为接近正弦波形,其中仙居顶处波动更为频繁。
(2) 受地表粗糙度的影响,华山观的α值普遍大于龙感湖;华山观α的极值出现时间与龙感湖相比,有明显的滞后,这可能是由于大气层结的差异引起的。
(3) 三种不同地形条件下,切变指数并没有表现出明显的冬春季节偏大,夏秋季节偏小的一般特点,且在不同的地形条件下有不同的特点。在复杂地形条件下,地形和下垫面的粗糙状况始终是影响局地风垂直切变的主导因素。
(4) 风速切变指数在风速较小时较大,且在不同地形条件下,不同风速段内切变指数变化表现出一致的趋势。在大风情况下,风速的垂直切变指数与一般情况下相比,均出现显著减小。
中华人民共和国建设部, 2002. 现行建筑结构规范大全修订缩印本[M]. 北京: 中国建筑工业出版社, 1-19.
|
申华羽, 吴思, 谢今危, 等, 2009. 近地层风能参数随高度分布的推算方法研究[J]. 气象, 35(7): 54-60. DOI:10.7519/j.issn.1000-0526.2009.07.008 |
赵鸣, 唐有华, 刘学军, 1996. 天津塔层风切变的研究[J]. 气象, 22(1): 7-12. DOI:10.7519/j.issn.1000-0526.1996.01.002 |
刘学军, 吴丹军, 1991. 城市建筑群对低层大气风速廓线影响的统计分析[J]. 气象, 17(7): 14-18. DOI:10.7519/j.issn.1000-0526.1991.07.003 |
石雪峰, 夏建新, 吉祖稳, 2007. 植被条件对近地表风速垂线分布的影响[J]. 中央民族大学学报(自然科学版), 16(1): 9-15. |
贺德馨, 陈坤, 张亮亮, 等, 2006. 风工程与工业空气动力学[M]. 北京: 国防工业出版社.
|
李宗凯, 潘云仙, 孙润桥, 1985. 空气污染气象学原理及应用[M]. 北京: 气象出版社, 82.
|
林肇信, 1991. 大气污染控制工程[M]. 北京: 高等教育出版社, 78-79.
|
邓家铨, 朱赛霞, 郑敏, 1989. 不同地形边界层风场特性及山谷风污染气象个例分析[J]. 热带地理, 9(4): 346-353. |
罗毅, 麦方代, 1992. 山体绕流和尾流区气态污染物输送扩散规律的研究[J]. 环境科学学报, 12(2): 157-167. |
韩素芹, 刘林贤, 谢以扬, 等, 2008. 利用255 m铁塔研究城市化对地面粗糙度的影响[J]. 气象, 34(1): 54-58. DOI:10.7519/j.issn.1000-0526.2008.01.008 |
 2010, Vol. 36
2010, Vol. 36 