2. 中国气象局气象探测中心,北京 100081;
3. 厦门市气象局,厦门 361012;
4. 南京大学大气科学系,南京 210093;
5. 安徽省气象局,合肥 230031
2. Meteorological Observation Center, China Meteorological Administration, Beijing 100081;
3. Xiamen Meteorological Bureau, Xiamen 361012;
4. Department of Atmospheric Sciences, Nanjing University, Nanjing 210093;
5. Anhui Meteorological Bureau, Hefei 230031
测雨雷达问世以来,估测降水一直是其主要目标。雷达有很高的空间分辨率,能够很好地反映降水的空间不均匀性,但雷达探测的是空中有效照射体积内降水粒子的瞬时状态,在估测地面降水时受到雷达参数、降水微物理过程、观测环境等众多因素限制。雨量计在点上可以较精确测量降水,但对降水场的结构描述受到雨量计站网布设密度的制约。因此,雷达联合雨量计估测降水一方面可以得到准确的降水场结构,另一方面可以从雨量站处获得雷达探测降水偏差,进而估计整个雷达探测降水场的系统性偏差和各个格点上的局地偏差。早在1975年Brandes[1]就引入Barnes客观分析方法估计降水,Koistinen等[2]加入距离因子对Brandes的方法进行了改进,Collier等[3]提出分区域校准方法,引入与降水类型有关的校准因子,以消除雷达与雨量计测量的降水之间的系统性偏差,这些偏差可能和距离、降水类型有关。更复杂一点的分析方法包括最优插值[4],Kriging法[5],Kalman滤波法[6],变分校准法[7]等,这些方法在消除系统性偏差的基础上,进一步消除格点上可能存在的局地偏差以及和时间相关的随机误差。针对业务应用的系统有基于美国WSR-88D PPS(Precipitation Processing System)的MPE(Multisensor Precipitation Estimation)系统[8]等。
自20世纪80年代以来,我国也持续开展了雷达雨量计联合估测降水的研究,开发了许多校准算法[9-10],这些算法的开发为我国建立自己的雷达雨量计联合估测降水业务系统奠定了基础。
我国新一代天气雷达网已经基本建成,各省雨量站网密度逐步提高,雷达在暴雨监测、预警中的作用将得到进一步发挥,新一代天气雷达定量降水估测集成系统(QPEGS)正是在这样的基础上发展形成的一套我国自行研制的雷达联合雨量计估测降水集成业务系统;文章第1部分介绍了系统的主要组成;第2部分给出最近几年QPEGS降水估测结果的评估。
1 系统组成在短时临近预警预报中,及时、准确、高分辨率的降水数据十分重要,雷达具有很高空间分辨率,雨量计具有很高的精度,畅通的计算机网络可以保证雷达和雨量计数据能够及时传送到数据处理平台,在此平台上,可以开展雷达雨量计联合估测降水业务工作。目前,在我国地区级单位,可以实时获得约一部雷达、100个雨量计数据;在省级,可以实时获得约5部雷达、1000个雨量计数据,QPEGS即是基于省级的数据平台开发而成。
QPEGS系统的主要功能模块如图 1所示,系统通过计算机网络,实时获取雷达体积扫描数据,结合最近1小时的雨量计数据,经过校准处理和集成,生成雷达探测范围内最近1小时的降水量分布。

|
图 1 QPEGS系统功能模块 Fig. 1 Schematic diagram of QPEGS |
图中“雷达基数据”为本地或通过网络获得的雷达数据,数据为新一代天气雷达数据格式,每个体扫至少由4个仰角组成,其中,最低仰角尽可能接近地面扫描,次低仰角上最好不会出现超折射和海浪回波;体扫时间间隔一般在6分钟左右,本系统目前最多可以同时处理7部雷达的体扫基数据。
雷达基数据由信号处理器直接生成,包含有信号噪声、非气象目标物回波、虚假气象回波等,“雷达资料预处理”的目标是要从雷达基数据出发,经过处理得到一个尽可能接近地面降水场的雷达回波分布。雷达资料预处理一般包括两部分内容:一部分和雷达站址有关,一部分和雷达站址无关。如:垂直廓线订正、波束遮挡订正等和雷达站址有关;无气象意义的回波/噪声消除、非气象目标物(超折射回波和海浪回波)的识别与消除、复合平面回波生成等和雷达站址无关。为使QPEGS具有较好的普适性,在资料预处理中只包括了上述和雷达站址无关的预处理项。
在一定假定条件下,雷达反射率因子Z和雨强I有简单的幂指数关系:
| $Z = A{I^b}$ | (1) |
其中,A, b为和雨滴谱有关的系数,这是雷达估测降水的理论基础。根据这一关系,由雷达反射率因子可以直接估算降水,不需要雨量计校准。然而,由于Z-I关系在很大程度上依赖于雨滴谱,不同的季节、不同的地点、不同的降水类型,雨滴谱都有较大变化,因此,不存在一个普适的Z-I关系。QPEGS采用Z-I关系和雨量计校准相结合的方法,用实测雨量计校准Z-I关系估算的降水,提高降水估测精度。尽管应用雨量计校准方法使Z-I关系的重要性大大降低,然而,Z-I关系获得的降水场是雨量计校准时的初值场,初值场的好坏对校准结果有明显影响[11]。因此,本地Z-I关系的优化还是必要的[12],QPEGS最多可预先设置10种不同的Z-I关系系数,用户可以根据本地历史资料统计获得Z-I关系,也可以使用比较通用的Z-I关系,如(200,1.6;300, 1.4), 甚至可以动态修改Z-I关系系数。“Z-I关系”模块实现雷达反射率因子和雨强之间的转换,本文中的A=300,b=1.4。
图 1中“雨量计数据”为用于校准的最近1小时降水量数据,数据的更新频率为1小时,最短10分钟,每部雷达周边最多可以同时有1000个有降水的雨量计用作校准。
由于Z-I关系本身的误差,以及雷达参数不稳定和降水微物理过程的影响,雷达反射率因子经过Z-I关系转换得到的降水场,还可能存在系统性偏差(平均场偏差)和局地偏差,需要进一步用雨量计校准,为此,QPEGS采用了如下校准方案:
(1) 为了消除雷达探测降水场中可能存在的系统性偏差,计算所有雨量站格点上雷达雨强Rr(Z-I关系获得)和雨量计雨强Rg之间的平均偏差B=
(2) 就某一个时次而言,平均校准可以消除雷达降水场相对于雨量计降水场的平均偏差。然而,一方面由于降水的时空不均匀性,由有限的雨量计格点上提取的平均偏差并不能代表真正的系统性偏差;另一方面,雨量计本身存在测量误差,不同雨强下的测量误差也不相同,因此,在一定时段(3个时次以上)的平均偏差序列上提取系统性偏差,估计并消除由于雷达雨量计测量系统本身以及降水场时空变化等因素引起的随机误差将更加合理。卡尔曼滤波器是一种线性无偏滤波器,用以消除测量系统中可能存在的高斯白噪声。这种校准方法通过对雷达雨量计降水偏差时间序列滤波,以期消除由于雷达雨量计系统、降水场不稳定等因素产生的随机误差[6]。
(3) 平均校准和卡尔曼滤波用以消除雷达探测降水场和雨量计测量降水场之间的系统性偏差,但在雷达探测范围内,由于受地形、下垫面、降水类型等各种因素影响,不同的时间,不同的地点,雷达探测降水场的偏差也不相同, 仅仅校准系统性偏差不能提高雷达在单点上的降水估测精度。最优插值方法利用任一格点(i, j)周边雨量计k(1~N)和雷达测量降水的偏差(Pkr-Pkg),估计该点的雷达测量降水偏差,从而实现对雷达探测值的校准,即:
| $P_{i,j}^a = P_{i,j}^r + \sum\limits_{k = 1}^N {{W_k}} \left( {P_k^g - P_k^r} \right)$ | (2) |
其中,上标a表示插值后的估测值,r为雷达探测值,g为雨量计测量值;N为周边雨量计总数,P为雨强,Wk为雨量计k的权重,该权重和雨量计的测量精度以及降水在雨量计k和格点(i, j)的空间变异性有关[10]。
在QPEGS系统中,上述校准方法既可以独立使用,也可以级联使用,以最大限度地消除系统性偏差和局地偏差。
作为对比,QPEGS还提供了变分校准方法[9],和最优插值类似,QPEGS通过寻找使目标函数最小的分析场,实现对雷达测量降水场的校准,这种方法也可以较好地修正局部偏差。
为了提高校准结果的稳定性和可靠性,防止由于波束遮挡、充塞和回波移动引起误差,在校准之前先要对雷达雨量计数据对进行质量控制,只有当雷达雨量计数据皆有雨,且两者相应的反射率因子差小于20 dBz(基于Z-I关系)时才参与校准,最终,每种校准方法都输出一个校准后的降水场。
经过“雨量计校准”模块处理后,QPEGS系统最多可生成校准后的降水场6个(平均校准、卡尔曼滤波、最优插值、变分、平均-卡尔曼滤波-最优、平均-卡尔曼滤波-变分),加上Z-I关系生成的降水场一共7个,用户可根据各方法特点和应用需求选用。然而,从一个实际降水场估测出如此多的降水场可能给用户带来使用上的困惑,为此,在各方法精度评估的基础上,用精度加权的方式将7个降水场合并成一个降水场,即“雨量集成”模块。用户可以选择集成以后的降水场作为系统输出,也可以选择其中任意1个或几个降水场作为输出,或进一步加工累积降水、最大估测降水、流域面雨量等应用产品。
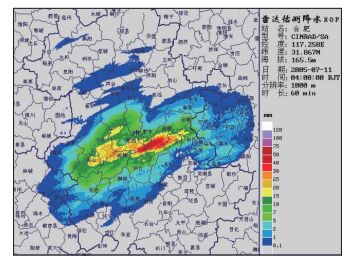
QPEGS的数据输入输出充分考虑与现有系统的兼容,可直接处理新一代雷达基数据,雨量计数据采用MICAPS数据格式Diamond 3,输出产品有1 h、3 h、6 h累积降水。输出格式有两种,一种为通用GIF图像格式,可以在任意环境下显示,如图 2所示;一种为专用数据格式,这种格式下的数据精度较GIF格式的高,用户可以在此基础上进一步开发应用产品。
|
图 2 QPEGS雷达降水估测系统小时降水量产品图 Fig. 2 Hourly precipitation products given by QPEGS radar system |
针对实际业务需求,QPEGS正常运行时无需人工干预,每10分钟或1小时自动生成最近1小时降水量产品,时间滞后不超过10分钟。
QPEGS主要技术指标:
降水估测时间分辨率:1 h
产品生成时间分辨率:10 min,1 h、3 h、6 h
数据空间分辨率:1 km×1 km
降水估测范围(半径):230 km
雨量数据精度:0.1 mm
输入雷达数据格式:SA/SB, CC/CD
输入雨量计数据格式:MICAPS Diamond 3
操作系统:Windows XP/2000
2 效果评估 2.1 评估数据安徽合肥CINRAD/SA雷达在2003、2005、2006年收集了大量的雷达降水资料,时间分辨率为6 min,同期还有地面自动雨量站1小时的实测降水数据,这为在较长时间段,较高分辨率上客观开展精度评估创造了条件,本文评估使用的资料如表 1所示。
|
|
表 1 评估样本数分布 Table 1 Number of samples for evaluation |
其中雨量站数是指有雨时参与评估的雨量站个数,雷达体扫数为降水时段雷达体扫数,总样本数为降水时段雷达探测范围内测量到降水的雨量站站时数,有效样本数为经过质量控制的样本数。2003年使用了水文站的雨量计数据,因此,雨量站的密度要远高于2005和2006年,且2003年的降水为两次相继的梅雨期降水过程,降水类型相似,2005和2006年的几次降水过程时间跨度较大。
2.2 评估方法为了客观地评估雷达估测降水系统的精度,本文以1小时降水量为基本单位, 构成以小时t和雨量站点位置j为变量的样本序列P(j, t), 在每个降水时次将有降水的雨量计数据随机地分为两组A和B,一组用于校准,另一组用于评估。评估数据通过下列步骤获得:
第一步:用A组数据校准,B组作为评估数据;
第二步:用B组数据校准,A组作为评估数据。
本文所分析的评估数据即为上述第一步和第二步评估数据之和。为了能够客观地评价QPEGS系统估测降水的精度,对评估数据作了一定的质量控制,具体包括:
(1) 剔除雨量计有降水,雷达没有回波的数据;这种情况通常是由于地形遮挡或距离太远导致雷达探测不到造成,这样的样本点不适合用于评估。
(2) 剔除野点;评估数据序列中可以提取出雷达雨量计小时雨量的偏差序列,从偏差序列可以计算均值和均方差,剔除3倍均方差的样本,这些点在统计上缺乏代表性。
经过上述处理后,共得到10303个有效样本对。
在小时降水时间序列基础上,按日和降水过程累加,得到日降水样本序列和过程降水样本序列,可以分析不同时间单位上的降水估测精度;为了客观比较不同方法、不同时间单位的估测精度,定义以下二个物理量:平均偏差:
| $B = \frac{1}{N}\sum\limits_{j = 1}^N {\left[ {\sum\limits_{t = 1}^T {{P_r}\left( {j,t} \right) - \sum\limits_{t = 1}^T {{P_g}\left( {j,t} \right)} } } \right]} $ | (3) |
平均相对误差:
| $E = \frac{1}{N}\sum\limits_{j = 1}^N {\frac{{\left[ {\sum\limits_{t = 1}^T {{P_r}\left( {j,t} \right) - \sum\limits_{t = 1}^T {{P_g}\left( {j,t} \right)} } } \right]}}{{\sum\limits_{t = 1}^T {{P_g}\left( {j,t} \right)} }}} $ | (4) |
其中,t为时间(单位为h),j为空间某一雨量站,T为雨量积分时间段,本文分别在小时(T=1), 日(T=24) 和过程(T=降水起止时段)时间段上开展评估,N为以时间段为单位的样本序列长度,Pr(j, t)为雷达估测小时降水量,Pg(j, t)为雨量计测量的小时降水量。
2.3 评估结果与讨论表 2给出了部分校准方法2003年估测降水误差随雨强的分布,作为比较,表中也给出了Z-I关系的结果。表中可见,所有雨量计校准方法的降水估测精度都比Z-I关系高,平均提高10%左右,降水估测精度最高的是卡尔曼最优插值,其次是最优插值、变分校准、卡尔曼滤波,平均校准方法的精度最低。经过校准,小时降水量的估测误差在40%左右,且2~20 mm/h降雨的校准效果要好于小于2 mm/h的降雨,校准可提高2~20 mm/h降雨的估测精度,但对于大于20 mm/h的降水,由于大雨区域较小,且2003年大雨样本平均距雷达站150 km,雷达探测回波和雨量站降水量空间一致性变差,相关下降,平均相对误差增大。
|
|
表 2 不同校准方法估测2003年降水平均相对误差E% Table 2 The mean relative errors (%) of different ealibration methods at various rain rate ranges in year 2003 |
由于雷达探测时为圆锥扫描,距离雷达越远,回波所在的高度越高。为了进一步分析QPEGS系统在不同距离上的误差,以卡尔曼最优插值组合方法(KOP)和等权重集成(EAV)为例,分析不同距离上的降水估测误差。
表 3为2003、2005、2006年降水估测误差与距离的关系,表中可见,0~150 km范围内的误差明显低于150~199 km距离上的误差,150 km以外,雷达回波高度较高,雷达反射率因子的分布不能很好反映地面降水分布,经邻近雨量计校准后,误差仍较大。大量雷达回波垂直廓线分布统计表明[13],回波强度随高度变化对降水估测有明显影响,尽管在QPEGS中,0~20 km和20~40 km距离分别使用了第4和第3个仰角的回波,以使估测降水的雷达回波尽可能处于同一高度,然而,表 3可见50 km以内经过雨量计校准后,雷达估测的降水量和雨量计相比依然偏低,一个可能的原因是这3年的样本集中在梅雨期,层状云降水较多,低层回波相对较弱。
|
|
表 3 雷达估测降水误差和距离的关系 Table 3 The bias and relative errors of radar estimation at different ranges |
表 4所示为2003、2005、2006年所有样本在不同时间尺度上降水量估测误差情况。
|
|
表 4 过程、日、小时降水量估测误差 Table 4 The bias and relative errors at different time spans |
随着降水累积时段的增加,降水估测误差逐渐减小,从小时降水近50%的误差,下降到过程降水的30%以下,由于2005、2006年数据为气象部门雨量站数据,2003年使用的数据为水文站雨量数据,水文站雨量计数量远远大于气象部门雨量站数量,为此,按年分别统计,以日降水为例。
可见,2003年的估计误差远小于2005、2006年,校准雨量站的数量可能是影响降水估测精度的关键因素。表 6给出了校准站数和误差的关系,针对小时降水数据,计算每个小时参与校准的雨量站数,校准雨量站越多,意味着雨区的面积越大。表中可见,随着校准雨量站数的增加,降水估测误差趋于减小。一般而言,参与校准的雨量站数越多,表明降水区域越大,降水的持续时间越长,此时的降水估测误差也趋于减小,说明1小时的雨量计降水累积和1小时的雷达回波累积有较好的一致性。
|
|
表 6 校准站数和误差的关系 Table 6 The bias and relative errors of radar estimation at different calibration gauges |
QPEGS针对新一代10 cm天气雷达降水估测开发,生成雷达探测范围内的小时降水量,时间分辨率10 min,空间分辨率1 km×1 km,产品滞后时间小于10 min。
评估表明,校准雨量计数量和估测精度有明显正相关,校准雨量计数越多,降水估测精度越高(表 5),2003年的小时降水估测误差约40%;雨量计密度保持不变的情况下,降水时段越长,降水估测的精度越高(表 4);降水区域越大,降水估测的精度也越高(表 6)。
|
|
表 5 不同年份日降水估计误差 Table 5 The bias and relative errors of daily radar estimation at different years |
QPEGS系统在资料处理过程中重点针对通用性问题,如噪声点、孤立回波块、超折射等进行订正。在资料处理和算法设计中尽管也考虑了距离对降水估测的影响,在平均校准和卡尔曼滤波校准中均按距离分段处理,但结果表明,距离和降水估测精度仍然有明显相关,距离越远,降水估测的精度越低(表 3)。
QPEGS系统可以在10 min内同时处理7部雷达,每部雷达周边1000个校准雨量计数据,系统实时、连续运行,无需人工干预,该系统目前可从网址http://www.atmo.pku.edu.cn(从北京大学物理学院进入大气科学系网站)下载。
在本系统基础上,用户可进一步生成最大/最小估测降水,流域面雨量,过程累积降水,暴雨预警等衍生应用产品。
Brandes E, 1975. Optimizing rainfall estimates with the aid of radar[J]. J Appl Meteor, 14: 1339-1345. DOI:10.1175/1520-0450(1975)014<1339:OREWTA>2.0.CO;2 |
Koistinen J and Puhakka T. An improved spatial gauge-radar adjustment technique[R]. Proc. 20th Conf. on radar meteorol., AMS, 1981, 179-186.
|
Collier C G, Larke P R, May B R, 1983. A weather radar correction procedure for real-time estimation of surface rainfall[J]. Quart J R Meteorol Soc, 109: 509-608. |
张培昌, 等, 1992. 最优化法求Z-I关系及其在测定降水量中的精度[J]. 气象科学: 333-338. |
Krajewski W F, 1987. Co-kriging radar-rainfall and rain gauge data[J]. J Geophys Res, 92(d8): 9571-9580. DOI:10.1029/JD092iD08p09571 |
Ahnert P R, Krajewski W F, and Johnson E R. Kalman filter estimation of radar-rainfall field bias[R]. In preprints 23rd Conf. On Radar Meteor, 1986, JP33-JP37.
|
Ninomiya K, Akeyama T, 1978. Objective analysis of heavy rainfalls based on radar and gauge measurement[J]. J Meteor Soc Japan, 50: 206-210. |
Young C B, Bradley A A, Krajewski W F, et al, 2000. Evaluating NEXRAD multisensor precipitation estimates for operational hydrologic forecasting[J]. J Hydrometeor, (1): 241-254. |
张培昌, 戴铁丕, 伍志芳, 等, 1992. 用变分方法校准数字化天气雷达测定区域降水量基本原理和精度[J]. 大气科学, 16(2): 248-256. |
李建通, 杨维生, 郭林, 等, 2000. 提高最优插值法测量区域降水量精度的探讨[J]. 大气科学, (2): 263-270. |
李建通, 郭林, 杨洪平, 2005. 雷达-雨量计联合估测降水初值场形成方法探讨[J]. 大气科学, (06): 1010-1020. DOI:10.3878/j.issn.1006-9895.2005.06.16 |
郑媛媛, 谢亦峰, 吴林林, 等, 2004. 多普勒雷达定量估测降水的三种方法比较试验[J]. 热带气象学报, (02): 192-197. DOI:10.3969/j.issn.1004-4965.2004.02.011 |
史锐, 程明虎, 崔哲虎, 等, 2005. 多普勒雷达实时反射率因子垂直廓线观测研究[J]. 气象, 31(9): 39-43. DOI:10.7519/j.issn.1000-0526.2005.09.008 |
 2010, Vol. 36
2010, Vol. 36 