2. 甘肃省武威市气象局,武威 733000
2. Wuwei Meteorological Office of Gansu Province; Wuwei 733000
目前基于数值预报产品释用的温度、降水分级等常规要素预报方法多数采用的是MOS、PP法等预报方法,数学模型普遍采用较为广泛使用的逐步回归和逐步判别方法,该方法计算简便快速,但在实际应用和理论上都发现有不足之处[1],当预报模型不合理或预报因子选取不适当时,预报效果比较差。本文用ECMWF(欧洲中期天气预报中心)数值预报产品作为武威市6个站点的最高、最低温度预报因子,采用PRESS(预测平方和)准则进行因子普查[1],逐步回归进行因子复选,最优子集回归[2-3]进行因子精选,确定最终建模的预报因子。由于大气环流对气温的影响是综合的,相互之间的关系是非线性的,基于误差反向传播学习算法(BP)的多层前馈型人工神经网络模型引入了多层隐层节点,解决了非线性样本问题,并具有高速度、强容错能力及稳健性等优良特征,已被广泛应用于信息处理、自动控制和管理工程等各个领域,在中、长期天气预报中的应用也有不少成功的例子[4],但在数值预报产品释用上的应用刚刚起步。本文尝试以ECMWF数值预报产品场的格点资料作为逐日最高、最低温度的预报因子,利用BP神经网络方法开展最高、最低温度预报的应用,比较线性回归模型与BP神经网络非线性模型的预报精度和优劣,为数值预报产品在温度预报上的释用提供有益的借鉴。
1 资料选取和资料处理 1.1 资料和关键区选取选取2003年3月1日至2008年12月31日20时的逐日ECMWF数值预报产品实况格点资料,网格距为2.5°×2.5°经纬度;层次为850 hPa、700 hPa、500 hPa,基本要素为位势高度(h)、温度(t)、相对湿度(rh)以及风速的u、v分量等。关键区为天气系统进入本区域将会对本市产生影响的区域,范围为35°~45°N、90°~110°E。预报对象为2003年3月1日至2008年12月31日武威市6个站点的逐日最高、最低温度,取自武威市6个地面观测站点的自动站记录。
1.2 插值处理由于从MICAPS下发的ECMWF数值预报产品的格距为2.5°×2.5°经纬度,而武威市各县区的间距为60~90 km。因此必须对格点资料进行插值处理。插值方法采用线性插值,对x、y方向分别进行线性插值,插值后的格点资料为1°×1°经纬度。插值公式为[5]:
| $ f(x) = f({x_0}) + \left[{f({x_1})-f({x_0})} \right]{\rm{d}}x $ | (1) |
| $ f(y) = f({y_0}) + \left[{f({y_1})-f\left( {{y_0}} \right)} \right]{\rm{d}}y $ | (2) |
式(1)、(2) 中f(x)、f(y)为格点场要素,dx、dy为格距,先进行东西向(x方向)线性内插,再进行南北向(y方向)线性内插。因为,格点场格距为2.5°,x1-x0=2.5°、y1-y0=2.5°,当dx、dy取0.4时,则x=x0+1°、y=y0+1°;当dx、dy取0.8时,则x=x0+2°、y=y0+2°,这样就将格距为2.5°×2.5°经纬度插值到了1°×1°经纬度的格距上。将关键区域35°~45°N、90°~110°E之间的格点资料进行1°×1°经纬度插值处理,共计11×21个格点。
1.3 预报因子中物理量的差分计算根据诊断分析、日常预报经验及文献中[5-6]的研究成果,从影响温度的要素入手,利用插值后的位势高度(h)、温度(t)、相对湿度(rh)以及风速的u、v分量等基本格点资料,应用差分方法计算vor(涡度)、div(散度)、td(露点)、t-td(温度露点差)、e(水汽压)、q(比湿)、Δt(24小时变温)、Δh(24小时变高)、qfdiv(水汽通量散度)、tadv(温度平流), voradv(涡度平流)、ωζ(垂直螺旋度)、qadv(湿度平流)以及θse(假相当位温)等。其中差分中的Δy为经向差分、Δx为纬向差分。对于1°×1°经纬度的差分格距,Δy≈111 km,由于Δx是随纬度的变化而变化的,在赤道附近Δx≈111 km,随着纬度的增高,Δx的间距减小,具体计算公式为:
| $ \Delta x = \left( {\pi \cdot R \cdot \cos \varphi } \right)/180 $ | (3) |
其中,式(3) 中R为地球半径约为6370 km,φ为格点所在的纬度(角度)。
通过多种组合值构造出多个具有经验性的预选组合因子,组合因子可以是不同层次、不同物理量的组合,也可以是多个物理量的代数运算结果,如上升运动项:div58=div500-div850(中低层水平辐散之差),ωζ(垂直螺旋度);中低层水汽项:rh=rh850+rh700(中低层平均相对湿度);水汽输送项:mup=rh+div78+dfdiv8(水汽通量散度垂直输送);综合指数项:θse850(低层假相当位温, 反映对流性不稳定)等(见表 1)。用关键区内的基本格点资料,差分得到的物理量格点资料以及通过多种组合值构造出多个具有经验性的因子,预报因子不但考虑了单个因子的贡献,还对格点进行组合,产生衍生因子,即同一种物理量场因子,不但单个格点作为一个候选因子,多个格点的代数和也作为一个候选因子,构造出6485个预报因子供预报方程进行初选,建立初选因子库。
|
|
表 1 预选预报因子表 Table 1 Preselecting forecast factors |
气温是敏感的气象要素,其变化取决于热量的收支状况及热量储存的增多或减少,受季节影响极大。因此在建立逐日最高、最低温度模型时,为了避免季节不同对温度的影响,分站点、分月分别建立预报模型。试验发现,预报模型在预报时段中,中间段预报效果较好,开始、结束段预报效果明显下降。为了确保每个预报模型在预报时段内均有较好的预报效果,在分月建立模型时,样本选取以月内逐日资料为基础,向上月和下月各延伸10天,确保预报模型在实际预报时段内均有好的预报效果。
2 预报因子选取 2.1 预报因子初选方案最高、最低温度预报因子初选采用PRESS准则。因为,PRESS准则既可以反映因子的拟合好坏,也可以衡量预测能力的好坏,用它可以选取预测能力较好的因子[2]。初选因子的标准为:① 预报因子与预报对象的rp≥0.2, ② 因子物理意义要清晰, ③ 同一因子场上至多选取5个因子。初选后的因子数控制80~100个之间。
对因子普查后得到的80~100个初选预报因子,用逐步回归方法精选出10~14个最优预报因子,作为进行最优子集回归的候选因子。
2.2 预报因子精选方案预报因子精选采用最优子集回归。最优子集回归选取的预报因子是全局最优,选取最优方程采用CSC双评分准则,当CSC达最大时相应的回归模型为最优[1-3]。最优子集回归穷尽所有因子搭配,若有p个因子,会得到2p-1个可能回归,从所有方程中优选出CSC评分最大的预报方程,当CSC评分接近时,挑选预报因子较少的那一个作为最终预报方程。为了提高计算机运算速度,将逐步回归精选的因子确定为10~14个,代入最优子集回归进行优选,最终选定4~5个因子,确定最优子集回归预报模型,并将最优子集回归方程中的4~5个预报因子作为BP神经网络预报模型的待用预报因子。利用上述方法分别精选出区域内6个站点1年中12个月的逐日最高、最低温度最优子集回归预报方程和BP神经网络模型的待用预报因子。
以民勤6—8月逐日最高、最低温度为例,表 2列出了民勤最高、最低预报模型精选出的预报因子,其中物理量后括号内数字(m, n)为某一物理量第m个因子到第n个因子的代数和。如t850(4, 9) 为850 hPa温度第4~9个格点值的代数和,e850(1, 1) 为850 hPa水汽压第1个格点值。
|
|
表 2 民勤6—8月最高、最低温度预报模型精选因子表 Table 2 The chosen factors of extreme temperatures forecast model at Minqin station from June to August |
温度是变化非常灵敏的气象要素,由表 2中列出的精选后预报因子可以看出:精选出的预报因子均为850 hPa的物理量,多为温度(t)、相对湿度(rh)、水汽压(e)、比湿(q)、温度露点差(t-td)等。t反映了近地面层的温度状况,为影响最高、最低气温变化的主导因子,rh、e、q、t-td反映了空气中水汽含量的多少,也表征空中云量的多少,特别是夜间云量对大气的辐射降温影响极大,引入湿度因子能更客观地反映逐日最高、最低温度的变化情况。这些入选的预报因子物理意义明确,在经验预报中这些因子也是预报最高、最低温度的首选因子。
2.4 预报因子和对象的标准化处理对选取的预报因子和预报对象采用T1=(T-Tmin)/(Tmax-Tmin)进行极差标准化,把它们变换到[0, 1]区间,从而达到消除因子之间因数值相差悬殊而造成的预报不稳定性,并存储其相应的最大值和最小值。
3 BP神经网络预报模型人工神经网络是近十几年得到迅速发展的一门非线性科学。它以抽象的人脑构造基本单元组成,模拟人脑的部分思维过程。由于气温变化具有很明显的非线性演变特征,神经网络方法具有很强的处理非线性问题能力,尝试用神经网络进行建模研究,以期提高气温预报的准确性。
3.1 基本原理BP人工神经网络属于前馈型网络(见图 1)。它是一类具有层次结构的网络模块,具有很强的近似数学的映射能力。BP人工神经元网络有两个阶段:第一阶段称为学习阶段,神经元网络根据输入输出样本训练调整各层之间的权值和阈值,使之达到一定的要求;第二阶段是运用阶段,通过输入层的输入,依据学习训练所得权值和阈值的作用,得到输出值即预报值[4-6]。

|
图 1 BP神经网络模型 Fig. 1 BP artificial neural network model |
建立区域内6个站点分月逐日最高、最低温度BP神经网络预报模型时,以2003年3月至2007年12月的分月资料数据作为训练样本用于建模,2008年1—12月的资料作为独立样本用于模型的效果检验。首先将最优子集方法选取的最高、最低温度的4~5个因子作为网络学习矩阵的输入,将对应的最高、最低温度作为期望输出,以此建立神经网络预报模型的学习矩阵[7-12]。然后,把学习矩阵加载到网络的输入端,进行网络学习训练。其中网络的各项参数为:(1) 惯性因子a,当全局误差值比上一次误差值下降时a≥1,否则0 < a < 1;(2) 学习因子b=0.1;(3) 隐层节点数为3;(4) 收敛误差取0.0125,总体误差稳定达到极小值时,结束训练。输出各联接权重系数及阈值,由确定的网络各联接权重系数及阈值参数和预报因子可以得到对历史样本的拟合数据;使用2008年逐日20时下发的ECMWF数值预报24~144 h的预报场格点资料进行试预报,通过输入层的输入,依据学习训练所得权值和阈值的作用,得到输出值即预报值数据。这些在[0, 1]区间的数值,利用存储区域内6个站点各月最高、最低温度的预报量最大、最小值,用极差标准化公式T=Tmin+(Tmax-Tmin)T1得到区域内6个站点各月逐日拟合最高、最低温度值以及2008年1—12月的逐日最高、最低温度预报值。
通过分析区域内6个站点12个月的逐日最高、最低温度BP神经网络模型的拟合率,按照预报值与实况值误差值在±2.0 ℃之间评定为温度预报正确,其拟合准确率均在0.82以上。
4 预报结果检验分析使用武威市6个站点分月最优子集神经网络预报模型对2008年1—12月逐日最高、最低温度进行业务试用。以区域内民勤2008年7月逐日最高、最低温度BP神经网络模型试用结果与最优子集回归预报模型效果检验为例进行对比分析。
温度预报准确率Ts计算公式:
| $ \mathop T\nolimits_s = \frac{{NA}}{{NA + NB}} $ |
其中, NA为预报正确的次数,即预报值与实况值的误差在±2 ℃之间的天数;NB为预报错误的次数,即预报值与实况值的绝对误差大于2 ℃的天数。
绝对误差计算公式:
| $ E = \frac{1}{n}\sum\limits_{i = 1}^n {\left| {\mathop g\nolimits_i-\mathop T\nolimits_i } \right|} $ |
其中g为预报值,T为实况值,n为总日数。
使用相同因子的民勤7月逐日最高温度最优子集回归预报方程如下:
Y=26.6720-2.7699E-02x1-1.0872x2+1.1013x3-1.8582x4
其中, x1为850 hPa相对湿度第5~7个因子的代数和;x2为850 hPa温度第1~3个因子的代数和;x3为850 hPa温度第1~5个因子的代数和;x4为850 hPa温度第4个因子的值。
民勤7月逐日最低温度最优子集回归预报方程略。
由表 3中可以看出,BP神经网络模型最高、最低温度在120小时内的预报准确率Ts均保持了较高水平,最高温度120 h内平均Ts为0.697、最低温度Ts为0.71,且在120小时内Ts稳定,最高温度24~120 h内Ts在0.774~0.613、最低温度Ts在0.742~0.677,可在业务预报中直接应用。总体上看模型对于最高、最低温度均有较好的预报效果。其中,最高温度优于最低温度,夏季优于冬季、南部优于中西部。
|
|
表 3 最优子集神经网络及最优子集回归模型预报效果检验结果 Table 3 Forecast test results of optimal subset neural network and regression prediction model |
BP神经网络最高、最低温度各时效预报效果均好于最优子集回归预报,BP神经网络最高温度120 h内平均Ts比最优子集回归高8个百分点、最低温度高14个百分点。最高温度BP神经网络模型短时效的预报效果优势明显;最低温度BP神经网络模型长时效的预报效果优势明显。
分析BP神经网络绝对误差,最低温度120 h内的平均误差为1.94 ℃,除120 h在2 ℃以上外,其余时次均≤2 ℃。各时次的绝对误差均小于最优子集回归,其平均误差比最优子集回归小0.4 ℃,说明模型在最低温度的预报上,无论预报准确率还是绝对误差均优于最优子集回归。最高温度120 h内的平均误差为2.07 ℃,其中24、48小时误差小于等于2 ℃,其余时次在2.09~2.28 ℃之间,各时次的绝对误差均大于最优子集回归,其平均误差比最优子集回归大0.44 ℃。造成BP神经网络模型最高温度预报准确率Ts高、绝对误差大的原因是:遇有冷空气影响本区域,气温下降,此时的日最高气温不是出现午后,而是出现在前一天的20时左右,由于BP神经网络对天气过程反应灵敏,当天气过程来临时,模型预报的是午后最高气温的值,而非20时左右的温度值,造成最高温度的实测值与预报值间的误差增大,个别较大的预报误差,影响到平均误差的加大;无天气系统影响本区域时,最高温度正常出现的时间为午后,系统能准确把握,武威市处于西北地区中部,晴好天气在一年中占多数,因此个别的预报误差,对预报准确率影响不大[8-12]。
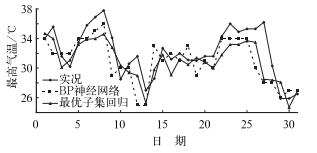
BP神经网络模型对明显的升降温过程反映敏感,不仅能较为准确地预报出升降温的趋势,也能较好地报出升降温的幅度以及极值点,特别对出现的破历史极值的最高、最低温度能很好地把握。如2008年7月8日(见图 2),BP神经网络模型和最优子集回归模型均预报出了气温升高的趋势,但BP神经网络模型的误差为1.8 ℃,最优子集回归模型的预报误差为3.2 ℃。
|
图 2 民勤2008年7月逐日日最高气温预报模型与实况对比 Fig. 2 Comparison of predited and observed daily maximum temperatures at Minqin Station in July 2008 |
(1) 采用诊断方法、因子组合和天气分型等手段建立预报因子库,更合理地描述了天气系统的发展机制。建立逐日最高、最低温度模型时,分站点、分月建立不同的预报模型,且每个月的预报因子和预报量选取向上月和下月各延伸10天,可确保预报时段内预报模型的稳定性。
(2) 用PRESS准则初选因子,最优子集回归精选因子,克服了其他方法筛选因子的不稳定性,因子拟合程度好、预测能力强,从而达到因子的全局最优。BP神经网络预报模型能较好地反映日极端温度的变化,预报模型具有较好的拟合和预报精度。模型投入试用以来,120 h内的平均预报准确率达较高水平,为ECMWF数值预报产品在温度上释用提供了一种好的思路和方法。
(3) BP神经网络模型具有较强的非线性处理能力,其预报精度和预报误差均比最优子集回归有一定的优势。对明显的升降温过程反应灵敏,升降温趋势和幅度预报较为准确,特别是对超出历史极值的升降温极值能较为准确地把握。对最高温度的预报能力优于最低气温,夏季优于冬季。当有天气过程影响时,最高、最低温度的预报误差明显加大,需要针对特殊天气增加判断条件,对模型直接输出结果进行修正。
(4) 建立的BP神经网络温度客观预报系统,定时从MICAPS后台调取资料,无需人工干预,方便预报员使用。
俞善贤, 1991. 一个着眼于预测能力及稳定性的因子普查方法[J]. 气象, 17(9): 40-43. DOI:10.7519/j.issn.1000-0526.1991.09.009 |
俞善贤, 汪锋, 1998. 试用最优子集与岭迹分析相结合的方法确定回归方程[J]. 大气科学, 22(12): 382-388. |
张万诚, 郑建萌, 解明思, 2000. 最优子集回归模型在低纬高原雨季开始期预报中的应用试验[J]. 气象, 26(11): 24-27. DOI:10.3969/j.issn.1000-0526.2000.11.005 |
陈宁, 金龙, 袁成松, 1999. 最优子集的神经网络预报建模研究[J]. 气象, 25(1): 14-19. DOI:10.7519/j.issn.1000-0526.1999.01.003 |
金龙, 吴建生, 林开平, 等, 2005. 基于遗传算法的神经网络短期气候预测模型[J]. 高原气象, 24(6): 981-987. |
中国气象局科教司, 1998. 省地气象台短期预报岗位培训教材[M]. 北京: 气象出版社, 75-111.
|
陈百炼, 2003. 降水温度分县客观预报方法研究[J]. 气象, 29(8): 48-51. DOI:10.7519/j.issn.1000-0526.2003.08.011 |
马学款, 普布次仁, 唐叔乙, 等, 2007. 人工神经网络在西藏中短期温度预报中的应用[J]. 高原气象, 26(3): 491-495. |
汤子东, 郑世芳, 奚秀芬, 1997. BP人工神经网络在春季降水量预报中的应用[J]. 气象, 23(8): 34-37. DOI:10.7519/j.issn.1000-0526.1997.08.007 |
蔡敏, 黄艳, 朱宵峰, 等, 2009. 基于BP神经网络的地质灾害细网格预报模型[J]. 气象, 35(7): 95-100. DOI:10.7519/j.issn.1000-0526.2009.07.014 |
张雪慧, 官莉, 王振会, 等, 2009. 利用人工神经网络方法反演大气温度廊线[J]. 气象, 35(11): 137-142. DOI:10.7519/j.issn.1000-0526.2009.11.018 |
许美玲, 段旭, 丁圣, 2009. 客观预报方程中因子的选取及应用效果分析[J]. 气象, 35(9): 112-118. DOI:10.7519/j.issn.1000-0526.2009.09.015 |
 2010, Vol. 36
2010, Vol. 36 