2. 四川省成都市气象局,成都 610072
2. Chengdu Meteorological Office, Chengdu 610072
在实现雷达基数据的进一步应用之前必须对其进行质量控制[1]。影响雷达数据质量最常见的一个重要因素就是地物杂波[2]。地物杂波对雷达数据的污染有两种来源:来自固定目标(例如, 建筑物、树木或者山脉)的正常传播(NP)时的地物杂波和在特定的大气条件下产生异常传播(AP)时的地物杂波[3]。如果这些杂波没有被滤除,它们就会进一步影响其他基于雷达基数据的二次产品以及雷达组网产品的质量。
现在的天气雷达一般在时域借助杂波图[4]使用无限脉冲响应(IIR)椭圆滤波器进行杂波抑制,即根据预先设定好的杂波位置进行滤波[5]。该方法的优点是计算量小,能够实现实时处理。但是它也存在两个缺点:一是由于滤波过程中存在暂态响应,降低了IIR椭圆滤波器本来应有的地物杂波抑制性能[6],使得IIR椭圆滤波器不能将地物杂波信号全部滤除,仍有一小部分将残留;二是在AP条件下会出现杂波区域抑制不全的情况。因为在AP条件下,杂波的强度和尺度发生了变化并可能出现新的杂波[7]。AP杂波会随着大气条件的变化而产生和消失,因此,AP目标是非固定的,变化的杂波,使用传统的固定的杂波图很难滤除。但随着雷达数据的使用越来越来广泛和复杂,要求信号处理系统几乎全部消除地物杂波[8],所以,迫切需要不需借助杂波图也能够实时判断出杂波位置并进行滤波处理的滤波器。
本文描述了IIR椭圆滤波器和自适应高斯频域滤波器(GMAP)的原理,并使用X-波段双极化多普勒天气雷达的数据分别对这两种滤波方法进行了测试和比较,初步的实验结果表明:不使用杂波图的自适应高斯频域滤波器的效果优于使用杂波图时的IIR椭圆滤波器,并且自适应高斯频域滤波器满足实时处理的要求。
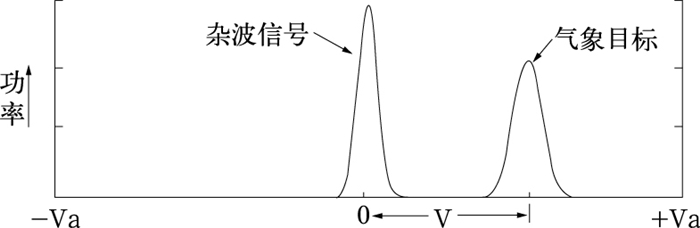
1 多普勒天气雷达回波信号的特征对地物杂波进行抑制之前,首先要知道多普勒天气雷达回波信号的特征。假设多普勒天气雷达回波信号只包含地物杂波和天气回波信号。在大多数情况下,相对于天气回波信号来说,地物杂波信号的谱宽很窄,且它们的平均多普勒速度基本为零。天气回波信号的平均多普勒速度会落在奈奎斯特速度区间内的任何地方,但通常不为零,即使在天气回波信号(零多普勒速度)和地物杂波重叠的情况下,天气回波信号的谱宽通常比地物杂波的谱宽要更宽一些, 如图 1所示[9]。根据杂波和天气的这些信号特征即可区别出杂波然后滤除。
|
图 1 用正态分布曲线描述的杂波和气象信号的功率谱 Fig. 1 Power spectrum of clutter and meteorological signal described by normal distribution curve |
IIR椭圆滤波器是一个时域数字滤波器,它通过对信号采样的叠加来完成滤波。
在多普勒天气雷达中,由于气象回波和地物杂波在谱上相距很近,有时甚至出现混叠,因此要求地物杂波滤波器具有很好的衰减特性且过渡带很窄,同时,由于地物杂波可能高于天气回波信号40~50 dB, 因而要求杂波滤波器具有很高的抑制度。而在IIR滤波器中椭圆滤波器具有最好的衰减特性且在较高抑制度下的过渡带最窄。因此,通常采用IIR椭圆滤波器进行杂波抑制[10]。
通常采用的IIR椭圆滤波器是一个5阶的高通滤波器,它对应的Z变换表达式为:
| $ \begin{array}{l} H\left( z \right) = {A_0} \cdot \left( {1 + {B_0}{z^{-1}}} \right)/\left( {1 + {D_0}{z^{-1}}} \right) \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\left( {1 + {A_1}{z^{-1}} + {D_1}{z^{ - 2}}} \right)/\left( {1 + {B_1}{z^{ - 1}} + {C_1}{z^{ - 2}}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\left( {1 + {A_2}{z^{ - 1}} + {D_2}{z^{ - 2}}} \right)/\left( {1 + {B_2}{z^{ - 1}} + {C_2}{z^{ - 2}}} \right) \end{array} $ | (1) |
其中,A0、A1、A2、B0、B1、B2、C1、C2、D0、D1、D2为滤波器系数。
根据杂波的强度、谱宽和脉冲重复频率,给出阻带衰减、阻带截止频率、通带起始频率和通带纹波,设计IIR杂波滤波器,即可得到所需的滤波器系数。
由于IIR椭圆滤波器的实现中存在暂态响应,会降低滤波器本来应有的地物杂波抑制性能。所以使用IIR椭圆滤波器进行杂波滤波也就会存在杂波残余。
3 自适应高斯频域滤波器从频域的角度来看,有意地将某些频率成分去掉的过程就叫做频域滤波。
频域滤波一般包括几个步骤,首先是得到信号的多普勒功率谱;其次,根据给出的地物杂波谱宽,确定杂波滤波器的槽口宽度,将槽口宽度内以零多普勒为中心的那些DFT系数置为零(这样做不仅去掉了包含在这些系数当中的地物杂波,同时也将去掉存在于这些系数中的天气回波信号功率);最后,根据没有滤掉的回波信号成分对槽口内插即可恢复损失的天气回波信号。下面将详细介绍自适应高斯频域滤波器的使用前提和实现步骤。
3.1 自适应高斯频域滤波器假设使用GMAP滤波时,对地物杂波、天气回波和噪声做出了以下假设[10-11]:
(1) 天气回波的谱宽大于地物杂波的谱宽。
(2) 多普勒谱包含地物杂波,一个单一气象目标和噪声。
(3) 地物杂波的宽度近似已知。假设的宽度用来决定要去除多少个内部杂波点。
(4) 地物杂波的形状近似为高斯型。这个形状用于计算去掉的内部杂波点的数目。
(5) 天气回波的形状近似为高斯型。这个形状用于重建叠加的天气回波中被滤掉的点。
3.2 自适应高斯频域滤波器算法描述(1) 加窗与离散傅里叶变换(DFT)
首先分别对I和Q数据加海明窗,然后进行离散傅里叶变换(DFT)。使用下式求得回波信号的功率谱:
| $ \begin{array}{l} {s_k} = {\left| {DF{T_k}\left\{ {{w_m}{s_m}} \right\}} \right|^2}/M\\ \;\;\;\; = {\left| {\sum\limits_{m = 0}^{M-1} {{w_m}{s_m}{e^{-j\left( {2\pi /M} \right)mk}}} } \right|^2}/M \end{array} $ | (2) |
其中,sm表示连续的复时间信号,wm表示窗函数,M表示采样点数。
(2) 测定噪声功率
通常,通过周期噪声功率测量获得谱噪声功率。然而,当地物杂波目标很强的时候,谱噪声功率不同于已测量的噪声功率。在这种情况下,杂波对所有频率上的功率都有影响,增大了谱噪声电平。产生这种现象的主要原因是窗的旁瓣中会带有很大的功率。
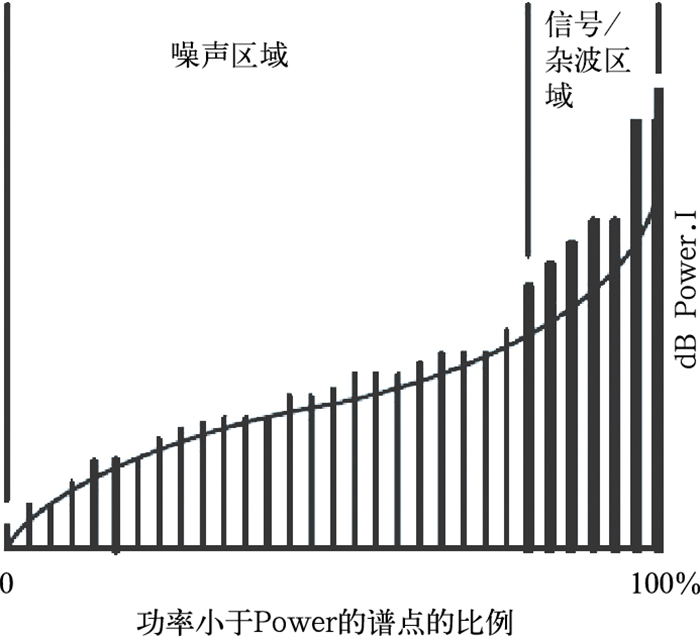
当不知道噪声功率或者当CSR>40 dB而需要利用布莱克曼窗重新计算时,最好用类似于Hildebrand等[12]的方法来计算。首先把多普勒谱分量按照它们的功率排序,如图 2所示。在排序中,功率最小的分量放在左边,功率最大的分量放在右边,纵轴代表的是各个分量功率的大小,横轴是各分量的归一化排序。然后,对5%至40%之间的功率求和,再对这个和取平均得到的值就设为噪声电平。
|
图 2 排序后的功率谱 Fig. 2 Power spectrum after sorting |
(3) 去除杂波点
这一步的输入是多普勒功率谱、假设的杂波宽度(单位为m·s-1)和噪声电平。利用三个中心谱点的总功率拟合一个具有标称谱宽的高斯信号。位于高斯信号和噪声电平之间的谱点就被置为噪声电平。
当三个中心谱点的功率和低于对应的噪声功率时,就认为没有杂波,所有的矩都利用矩形窗计算。如果三个中心谱点的功率只稍微高于噪声电平,只需去掉中心点(DC)。因为如果没有杂波的话,我们会希望不做滤波或者最差也只是去掉了中心谱点。
(4) 替换杂波点
高斯谱的假设用于替换被杂波滤波器去掉的点。从(2) 已知哪些谱分量是噪声,从(3) 已知哪些谱分量是杂波,假设剩下的都是天气回波。利用这些成分做离散傅里叶逆变换可以得到0阶和1阶自相关。利用脉冲对处理计算平均多普勒速度和谱宽(注意:由于已经去掉了噪声,所以不需要作噪声纠正)。然后根据计算的参数,应用高斯模型来决定在第三步中去掉的每个谱分量的替代值。
因为第一次替换的值通常不是很准确,所以算法需要利用原来的点和替代点重新计算R0和R1以生成新的替代点。重复操作直到两次连续操作的功率之差小于0.2 dB且速度差异小于奈奎斯特间隔的0.5%。
(5) 检查窗,如有需要,重新计算谱矩
从(3) 中可知去掉的杂波功率,从(4) 中可知天气回波分量和噪声,从而可以计算CSR。用该CSR值决定使用海明窗是否最合适。
如果CSR>40 dB,加布莱克曼窗重复自适应高斯频域滤波器的滤波过程和动态噪声计算;如果CSR>20 dB,加布莱克曼窗重复自适应高斯频域滤波器的滤波过程。如果CSR>25 dB,取布莱克曼窗的结果;如果CSR<2.5 dB,加矩形窗重复自适应高斯频域滤波器的滤波过程;如果CSR<1 dB,就取矩形窗的结果;其他情况下取海明窗时的结果。
自适应选择窗的好处是:在杂波功率没有泄露的情况下,利用主瓣最窄的窗计算谱矩,使得矩估计的方差最小。
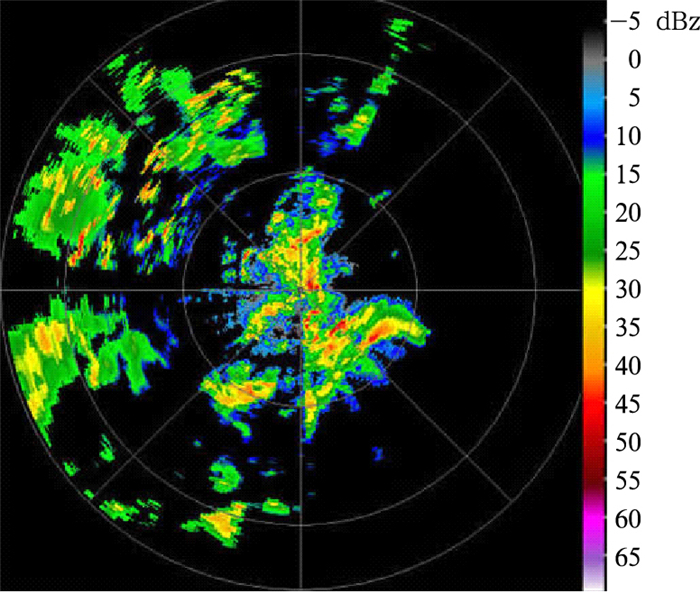
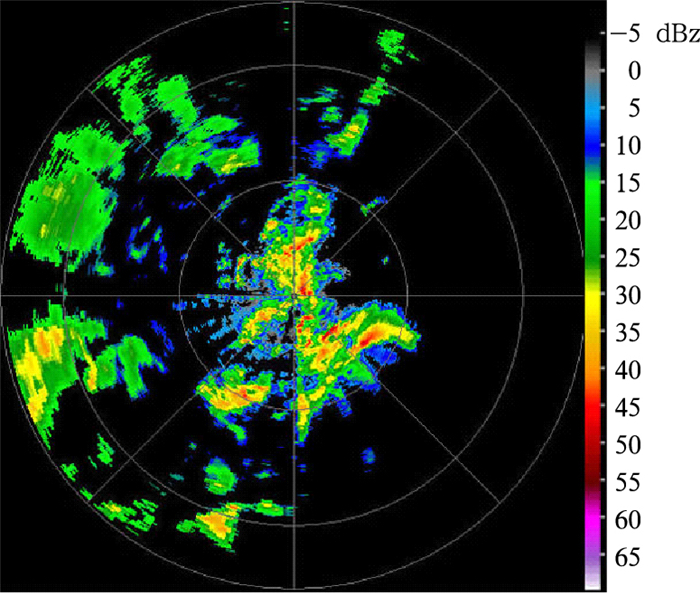
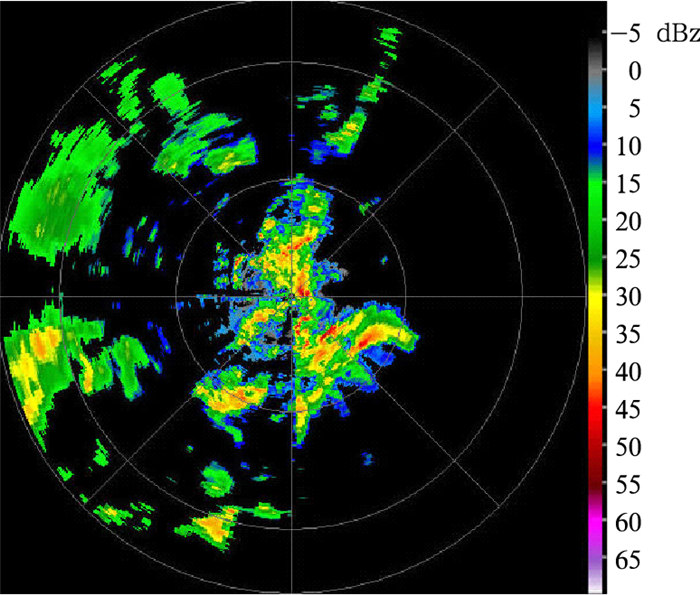
4 滤波效果的实例分析本文的实验数据从位于成都信息工程学院的X波段双极化多普勒天气雷达获取。图 3到图 5是根据2008年7月20日19时53分的1.9°仰角数据得到的反射率因子,3幅图中靠近雷达中心的两个距离圈分别表示50 km,最外面的距离圈表示27 km。其中图 3为未滤波的反射率因子。从图 3可以看出:在雷达的西北方向散布一些很强的由山脉产生的杂波。图 4是根据预先设定的杂波图,使用5阶IIR椭圆滤波器滤波后的反射率。从图中可以看出:虽然已经看不到很强的杂波存在,但是对应于图 3中出现杂波的位置仍有部分杂波残余。图 5是在没有使用杂波图的情况下,使用自适应高斯频域滤波器得到的反射率。由图 5可以看出:虽然此时没有使用杂波图,但对天气回波并没有产生衰减,并且出现杂波的地方滤波后没有杂波残余。显然自适应高斯频域滤波器的效果要优于5阶椭圆滤波器。通过把该方法应用于成都信息工程学院的X波段双极化多普勒天气雷达的信号处理中,证明自适应高斯频域滤波器满足实时处理的需求。
|
图 3 未滤波的反射率因子 Fig. 3 Unfiltered reflectivity |
|
图 4 使用IIR椭圆滤波器滤波后的反射率因子 (using fifth-order elliptic IIR filter) Fig. 4 Filtered reflectivity |
|
图 5 使用自适应高斯频域滤波器滤波后的反射率因子 (using GMAP filter) Fig. 5 Filtered reflectivity |
本文详细描述了自适应高斯频域滤波器的原理,并使用来自X波段的双极化天气雷达数据对其滤波效果进行了验证。结果表明:使用自适应高斯频域滤波器滤波,不需要预先建立杂波图也能在不损失天气回波的条件下得到很好的滤波效果,并且满足实时处理的要求。
若将该技术应用到实际业务中,首先要满足前文所描述的自适应高斯频域滤波器的使用前提。其次,因为相对于时域的IIR椭圆滤波器而言,自适应高斯频域滤波器的计算复杂度要大得多,为了满足实时处理的需求,可以使用专用的高速信号处理器以及提高离散傅里叶变换速度的算法。
鉴于本文只是对自适应高斯频域滤波器的初步研究,肯定还有值得进一步改进和提高的地方。希望通过长期的分析验证,能够使用自适应高斯频域滤波器替代传统的杂波图与滤波器相结合的滤波方式。
张志强, 刘黎平, 王红艳, 等, 2008. 华北区域四部雷达探测强度与定位一致性分析[J]. 气象, 34(9): 22-28. DOI:10.7519/j.issn.1000-0526.2008.09.003 |
王红艳, 刘黎平, 肖艳娇, 等, 2009. 新一代天气雷达三维数字组网软件系统设计与实现[J]. 气象, 35(6): 13-19. DOI:10.7519/j.issn.1000-0526.2009.06.002 |
张沛源, 杨洪平, 胡绍萍, 2008. 新一代天气雷达在临近预报和灾害性天气警报中的应用[J]. 气象, 34(1): 3-11. DOI:10.7519/j.issn.1000-0526.2008.01.001 |
黄炎, 邵玲玲, 葛张全, 1999. WSR-88D多普勒天气雷达的运行设计和使用情况分析[J]. 气象, 25(5): 13-18. DOI:10.7519/j.issn.1000-0526.1999.05.003 |
刁秀广, 朱君鉴, 杨传凤, 等, 2005. 济南CINRAD/SA雷达杂波抑制方案实施[J]. 山东气象, 25(4): 26-29. |
Zrnic D, 1999. Ground clutter canceling with a regression filter[J]. Atmospheric Technology, 16: 1364-1372. DOI:10.1175/1520-0426(1999)016<1364:GCCWAR>2.0.CO;2 |
Kessinger C, Ellis S and J Van Andel. The radar echo classifier: a fuzzy logic algorithm for the WSR-88D[G].3rd Conference on Artificial Intelligence Applications to the Environmental Science, AMS, 2003. https://ams.confex.com/ams/annual2003/webprogram/Paper54946.html
|
梁海和, JingZhongqi, 徐宝祥, 2006. NEXRAD的技术升级和发展方向[J]. 气象, 32(1): 3-11. DOI:10.7519/j.issn.1000-0526.2006.01.001 |
何建新, 姚振东, 郭在华, 2004. 现代天气雷达[M]. 成都: 电子科技大学出版社, 206-207.
|
刘艳. 多普勒天气雷达地物杂波时域和频域抑制研究[D]. 中国优秀硕士学位论文全文数据库, 2007: 15-16, 38-44. http://cdmd.cnki.com.cn/Article/CDMD-10621-2007179095.htm
|
Siggia A D, Passarelli Jr R E, 2004. Gaussian Model Adaptive Processing (GMAP) for Improved Ground Clutter Cancellation and Moment Calculation[J]. 3rd European Conference on Radar Meteorology: 67-73. |
Hildebrand P H, Sekhon R S, 1974. Objective determination of noise level in Doppler spectra[J]. Atmospheric Science, 13: 808-811. |
 2010, Vol. 36
2010, Vol. 36 