2. 中国气象局气象探测中心,北京 100081
2. Meteorological Observation Center of China Meteorological Administration, Beijing 100081
近几十年,随着气象仪器自动化程度的提高,多种遥测与遥感技术得到应用,一个崭新的现代地球大气探测系统已形成[1]。常规的高空气象探测系统主要包括地面探空雷达、探空气球、探空仪三个部分[2],但目前常规探测手段在海洋及其他偏远地区(如沙漠)缺少数据,其时空分辨率限制了对地球大气的时变特性和空间分布的深入认识,利用高分辨率的非常规资料势在必行。GPS掩星技术提供了一种新的大气探测手段,即对GPS无线电波信号进行处理,反演大气参数的垂直分布。由于无线电波经济低廉,探测精度高,不受降水和云层的影响,无系统长期漂移,具有长期的稳定性,可用于大气长期变化的监测[3]。
2006年4月15日,美国和台湾地区合作发射了COSMIC(Constellation Observation System for Meteorology,Ionosphere and Climate)气象、电离层和气候观测星座进行GPS掩星星座业务探测试验[4]。COSMIC星座由6颗LEO卫星组成,当GPS卫星信号穿过地球大气层时,电波射线因折射发生弯曲,LEO卫星接收该信号,根据几何光学原理得到GPS信号在各大气路径上的弯曲角,处理得到大气各层折射率,进而反演出全球大气温、压、湿和电离层廓线资料[7, 11, 15]。
空基GPS提供了大量的三维观测资料,如何把这些资料同化应用到气象业务中,是空基GPS气象学研究的重点之一[5],因此对COSMIC数据进行误差分析和质量控制是十分必要的,Rocken等利用2001年12月CHAMP和SAC-C掩星数据进行分析,得出冬季CHAMP和SAC-C掩星数据的偏差, 在5~25 km高度范围内,与ECWMF模式和NCEP/AVN模式相比,折射率标准差小于1%[6]。Syndergaard[8-9, 12]对GEOS卫星反演大气参数误差的分析中发现,忽略地球的非球形导致40 km以下的高度反演的温度出现偏差,并且向下逐渐增大,极端情况下10 km可达3 ℃,到达地面可达6 ℃。MicroLab1的观测数据与欧洲中尺度天气预报中心ECMWF的分析结果和临近的探空气球站的观测资料相比,在5~30 km,温度精度好于1.5 ℃。为了考察COSMIC掩星数据的误差特点,本文在比对时运用了不同的参考资料L波段精密探空数据。由于常规探空的特性层和规定层(100 hPa以下12层)数据会遗漏大气中细微的变化特征,为克服常规探空垂直层数的局限性,采用L波段精密探空数据(垂直层数达到几千层)与COSMIC比对分析,将2008年5月20日至2008年11月26日COSMIC数据的干廓线资料(atmprf)和湿廓线资料(wetprf)进行分析,研究COSMIC反演资料在温度、气压、折射率等方面与探空秒数据对比的偏差和均方根误差[10],探讨干湿反演资料的误差特点。为气象工作者使用COSMIC数据提供参考,为我国数值天气预报模式同化提供误差分析等依据。
1 COSMIC数据反演方法和资料来源LEO卫星上的GPS双频接收机能够记录精确的双频GPS信号相位延迟量和信噪比。从相位延迟序列,通过简单的时间差分,可得到大气多普勒漂移序列。用已知的精密GPS和LEO卫星轨道信息,可利用大气多普勒漂移序列计算出GPS信号的弯曲角碰撞参数的变化函数。假设地球大气介质局部球对称,用Abel积分逆变换把弯曲角序列反演得到大气折射指数剖面。然后利用理想气体状态方程、流体静力学方程和Smith-Weintraub大气折射率方程,从折射指数剖面反演得到气象参数:对于理想大气而言,折射率N、气压p、温度T及水汽压e存在关系式
| $\begin{align} N = &77.6 \times \left( {\frac{p}{T}} \right) + 22.0 \times \left( {\frac{e}{T}} \right) +\\& 3.739 \times {10^5}(\frac{e}{{{T^2}}})\end{align} $ | (1) |
式(1)中右边第一项是干空气对折射率的贡献,第二、三项是水汽的贡献。
当水汽可以忽略的情况下,则有
| $ N = 77.6\frac{p}{T} $ | (2) |
根据大气状态方程和静力方程等,可以得到以下反演大气参数的方程:
| $ \rho = 0.003484\frac{p}{T} = 4.4897 \times {10^{ - 5}}N $ | (3) |
| $ \frac{{\delta p}}{{\delta z}} = - \rho g $ | (4) |
| $ T = 77.6\frac{p}{N} $ | (5) |
其中ρ为大气密度,g为局部重力加速度。由折射率廓线根据公式(3)可以得到大气密度分布,进而通过公式(4)积分得到气压廓线,为干空气气压(hPa),在水汽忽略的情况下,由理想气体状态方程(5)可得到温度廓线,这样反演的温度为干空气温度(K)。
当水汽的贡献不可忽略时,会出现GPS掩星技术的水汽模糊问题。一般温度T通过其他独立的途径获得(如可从模式中获得温度剖面),湿空气的状态方程为
| $ p = \rho {\rm{ }}{R_d}\left( {T + 0.378\frac{e}{p}T} \right) $ | (6) |
其中Rd为干空气的比气体常数,Rd=287.05 J·kg-1·K-1,利用公式(1)、(4)、(6),计算可获得气压p和水汽压e。
本文使用2008年5月20日至2008年11月26日的COSMIC数据。COSMIC数据为nc文件(即netcdf文件,网络通用数据格式),数据来源于http://www.cosmic.ucar.edu/,网站可提供近实时COSMICRT(cosmic real time)产品和COSMIC后处理产品,后处理产品大约6星期后可得到。COSMIC大气廓线产品分为4级,采用前2级数据,如表 1所示。
|
|
表 1 COSMIC大气廓线资料 Table 1 List of COSMICatmospheric profile data |
为了分析水汽压和折射率廓线,利用L波段探空探测到的温度、气压、相对湿度数据按如下方法计算得到水汽压、折射率数据。
根据马格纳斯(Magnus)计算饱和水汽压经验式:
| $ {E_s} = {E_0} \times {10^{\frac{{at}}{{b + t}}}} $ | (7) |
式中Es为温度t时饱和水汽压(hPa);E0是温度为0 ℃时的饱和水汽压,通常取E0=6.11 hPa;a、b为常数,由于探空仪测定和计算相对湿度时都是相对水面的,因此常数a、b选取对于水面a=7.63,b=241.9。
根据相对湿度公式
| $ f \approx \frac{e}{{{E_s}}} \times 100\% $ | (8) |
式中e、Es为空气块实有水汽压和饱和水汽压。进而得到空气块的水汽压e。由公式(1)、(7)、(8)即可计算出折射率廓线。
由公式(8)可得空气实际水汽压,
| $ e \approx f \times {E_s} $ | (9) |
式中f为相对湿度,Es为饱和水汽压(hPa)。根据L波段探测的相对湿度和温度廓线即可计算得到L波段探空的水汽压廓线。
资料中干廓线资料垂直层数3000~5000层,湿廓线资料垂直层数400层,因此干湿廓线资料能反映大气细微的变化特征。
2 对比分析方法计算偏差和均方根误差,分别有如下公式:
| $ d = \frac{1}{n}({x_i} - {y_i}) $ | (10) |
| $ s = \sqrt {\frac{{\sum\limits_{i = 1}^n {{{\left[ {({x_i} - {y_i}) - \overline {({x_i} - {y_i})} } \right]}^2}} }}{{n - 1}}} $ | (11) |
式中xi为临近的COSMIC掩星点的反演数据,yi为探空站的观测资料。
以中国区域L波段探空资料为基准,选取与探空记录在时间和空间范围内匹配的COSMIC资料进行对比分析。由于掩星点的变化在百千米的量级,时间间隔几分钟,L波段探空点的空间间隔在几十千米,时间间隔约1.5小时,而地球上1纬度约为实际距离110 km,1经度代表的距离小于110 km,为了选取掩星点临近的L波段探空数据,试验选取的时空条件是经度、纬度分别小于1度,时间小于3小时。L波段探空数据垂直可达到几千层,干温度廓线资料垂直层数最多可达5000层,为使两种数据在相同的高度层上进行比较,在高度的处理上采用线性插值的方法,在从地面到30 km的高度范围内干廓线资料平均插值到6000层上,湿廓线资料插值到300层上。在2008年5月20日至2008年11月26日的时间范围内共匹配出符合条件的120对干湿廓线。
3 COSMIC数据的误差检验COSMIC大气廓线产品包括干湿廓线资料,区别在于是否考虑水汽的存在,同时干廓线资料的垂直分辨率远大于湿廓线资料。
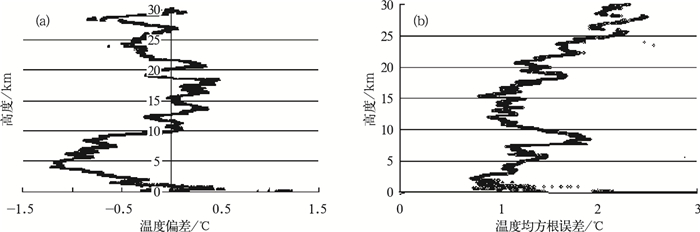
3.1 湿廓线的误差检验 3.1.1 温度误差图 1是COSMIC资料的温度廓线与L波段探空资料的温度廓线在各层的偏差值和均方根误差值,10 km以下温度的平均偏差为-0.5 ℃,均方根误差为1.5 ℃;整层平均偏差为-0.3 ℃,均方根误差为1.7 ℃;10 km以上温度的偏差为-0.2 ℃,均方根误差为1.9 ℃。
|
图 1 COSMIC湿廓线的温度与L波段探空匹配后的误差特点 (a) COSMIC温度与探空匹配后的各层偏差; (b) COSMIC温度与探空匹配后的各层均方根误差 Fig. 1 Temperature error characteristics between COSMIC and radiosonde soundings (a) Temperature bias in the different altitude between COSMIC and radiosonde soundings; (b) Temperature RMS in the different altitude between COSMIC and radisonde soundings |
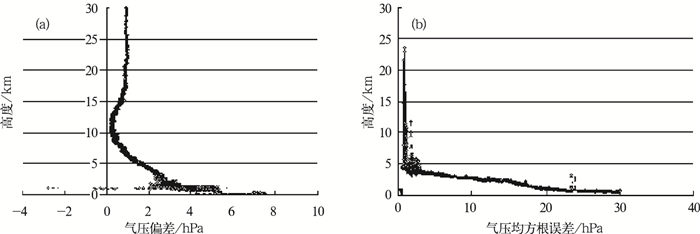
图 2是COSMIC数据的气压与L波段探空资料的气压数据在各层的偏差值和均方根误差值,在10 km以下,气压偏差为2.0 hPa,均方根误差为4.7 hPa;整层偏差为1.5 hPa,均方根误差为3.3 hPa,在10 km以上,气压偏差为1.3 hPa,均方根误差为2.6 hPa。
|
图 2 COSMIC湿廓线的气压与L波段探空匹配后的误差特点 (a) COSMIC气压与探空匹配后的各层偏差; (b) COSMIC气压与探空匹配后的各层均方根误差 Fig. 2 Pressure error characteristics between COSMIC and radiosonde soundings (a) Pressure bias in the different altitude between COSMIC soundings and radiosonde; (b) Pressure RMS in the different altitude between COSMIC and radiosonde soundings |
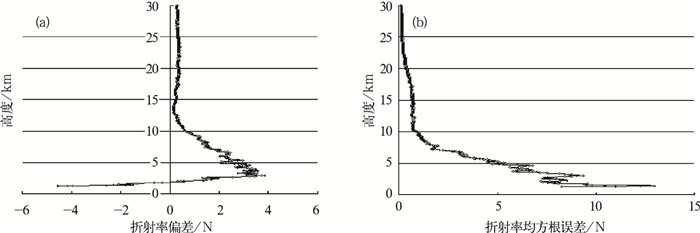
图 3是探空计算的折射率与COSMIC数据反演的折射率在各层的偏差值和均方根误差值,从图 3可以看出,在10 km以下平均偏差1.4N,均方根误差为5.9N;在10 km以上折射率偏差较小,平均偏差为0.4N,均方根误差为0.9N;折射率整层的平均偏差为0.8N,均方根误差2.6N。可见,COSMIC折射率的误差较小。
|
图 3 COSMIC湿廓线的折射率与L波段探空匹配后的误差特点 (a) COSMIC折射率与探空匹配后的各层偏差; (b) COSMIC折射率与探空匹配后的各层均方根误差 Fig. 3 Refractivity error characteristics between COSMIC and radiosonde soundings (a) Refractivity bias in the different altitude between COSMIC and radiosonde soundings; (b) Refractivity RMS in the different altitude between COSMIC and radiosonde soundings |
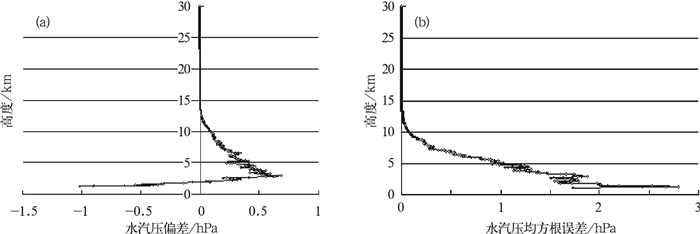
图 4是探空计算得到的水汽压与COSMIC数据反演的水汽压匹配后在各层的平均偏差值,在10 km以下水汽压平均偏差为0.1 hPa,均方根误差为1.1 hPa。
|
图 4 COSMIC湿廓线的水汽压与L波段探空匹配后的误差特点 (a) COSMIC水汽压与探空匹配后的各层偏差; (b) COSMIC水汽压与探空匹配后的各层均方根误差 Fig. 4 Vapor pressure error characteristics between COSMIC and radiosonde soundings (a) Vapor pressure bias in the different altitude between COSMIC and radiosonde soundings; (b) Vapor pressure RMS in the different altitude between COSMIC and radiosonde soundings |
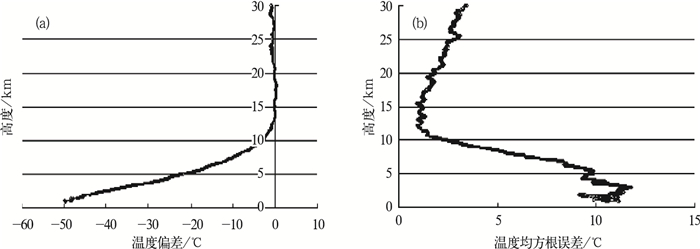
图 5是COSMIC的干温度与探空资料的温度数据在各层的偏差值和均方根误差值,从图 5可以看出,在10~30 km温度的平均偏差为-0.3 ℃,均方根误差为1.9 ℃,在10 km以下,由于大气中水汽的影响,出现较大的偏差,平均偏差为-19.8 ℃,均方根误差为10.1 ℃,整层温度平均偏差为-6.8 ℃,均方根误差为4.6 ℃。
|
图 5 COSMIC干廓线的温度与L波段探空匹配后的误差特点 (a) COSMIC温度与探空匹配后的各层偏差; (b) COSMIC温度与探空匹配后的各层均方根误差 Fig. 5 Temperature error characteristic between COSMIC and radiosonde soundings (a) Temperature bias in the different altitude between COSMIC soundings and radiosonde; (b) Temperature RMS in the different altitude between COSMIC and Soundings |
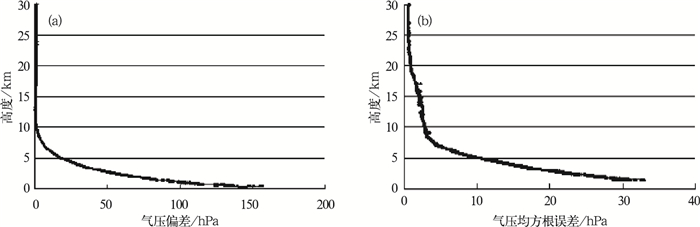
图 6是COSMIC的干气压廓线与探空资料的气压数据在各层的偏差值和均方根误差值,从图 6可以看出,在10 km以上气压偏差较小,10~30 km气压的偏差的为1.4 hPa,均方根误差为2.6 hPa;在10 km以下,气压偏差为25.8 hPa,均方根误差为16.0 hPa。整层气压平均偏差为9.5 hPa,均方根误差为7.1 hPa。
|
图 6 COSMIC干廓线气压与L波段探空匹配后的误差特点 (a) COSMIC气压与探空匹配后的各层偏差; (b)COSMIC气压与探空匹配后的各层均方根误差 Fig. 6 Pressure error characteristics between COSMIC and radiosonde soundings (a) Pressure bias in the different altitude between COSMIC and radiosonde soundings; (b) Pressure RMS in the different altitude between COSMIC and radiosonde soundings |
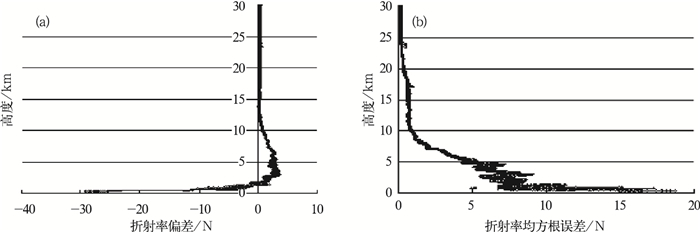
图 7是COSMIC的折射率廓线与探空资料计算的折射率数据在各层的偏差值和均方根误差值,从图 7可以看出,平流层折射率偏差较小,经计算,10 km高度以上,折射率偏差为0.4N,均方根误差为0.9N;而在10 km高度以下,折射率偏差为1.6N,均方根误差为6.2N。整层折射率平均偏差为0.8N,均方根误差为2.7N。
|
图 7 COSMIC干廓线折射率与L波段探空匹配后的误差特点 (a) COSMIC折射率与探空匹配后的各层偏差; (b)COSMIC折射率与探空匹配后的各层均方根误差 Fig. 7 Refractivity error characteristics between COSMIC and radiosonde soundings (a) Refractivity bias in the different altitude between COSMIC and radiosonde soundings; (b) Refractivity RMS in the different altitude between COSMIC and radiosonde soundings |
(1) COSMIC湿廓线资料与L波段探空相比,在10 km高度以下,比较一致,温度偏差为-0.5 ℃,均方根误差为1.5 ℃;气压偏差为2.0 hPa,均方根误差为4.7 hPa;水汽压偏差为0.1 hPa,均方根误差为1.1 hPa;折射率偏差为1.4N,均方根误差为5.9N。表现了较小的偏差和均方根误差。
(2) 在10~30 km高度内,水汽含量很小,COSMIC干廓线资料的温度、气压偏差较小,温度偏差为-0.3 ℃,均方根误差为1.9 ℃;气压偏差为1.4 hPa,均方根误差为2.6 hPa;折射率偏差为0.4N,均方根误差为0.9N。
(3) 本文的分析结果与其他的分析基本一致[13],与Kuo等[14]的结果存在一些差异,特别是在对流层顶处。
(4) COSMIC高垂直分辨率的干湿廓线资料,为研究对流层和平流层的大气细微的变化提供了新的数据来源。
本工作主要是对中国境内30 km高度以下的数据误差分析,资料匹配的原则是选择与COSMIC掩星事件临近的探空点进行对比分析,时间间隔3小时,COSMIC时间为一次掩星事件的中间时刻,而L波段时间为一次探空的起始时间,在误差的统计中包括了这种对比点的时间和空间上的差异,存在一定的算法误差。同时没有区分不同纬度的资料,这还需要进一步的研究,为质量控制提供更详细的空间分布的误差信息,将质量控制后COSMIC掩星观测得到的弯曲角或折射率信号同化到数值模式中,为数值天气预报服务,也是今后研究的方向。
致谢:感谢UCAR的COSMIC CDAAC为本文提供相关的掩星观测数据,中国气象局气象探测中心郭启云为本文提供L波段探空数据,王海深提供有关文献资料。
宋连春, 李伟, 2008. 综合气象观测系统的发展[J]. 气象, 34(3): 3-9. DOI:10.7519/j.issn.1000-0526.2008.03.001 |
李伟, 邢毅, 马舒庆, 2009. 国产GTS1探空仪与VAISALA公司RS92探空仪对比分析[J]. 气象, 35(10): 97-102. DOI:10.7519/j.issn.1000-0526.2009.10.012 |
杜晓勇, 毛节泰, 2008. GPS-LEO掩星探测现状和展望[J]. 高原气象, 27(4): 918-931. |
Zou X, Zhen Zeng. A quality contral procedure for GPS radio calculation data[J].Journal of Geophysical Research, 111, D02112, doi:10.1029/2005JD005846, 2006. http://adsabs.harvard.edu/abs/2006JGRD..111.2112Z
|
曹云昌, 方宗义, 夏青, 2004. 地空基GPS探测应用研究进展[J]. 南京气象学院学报, 27(4): 565-572. |
Christian Rocken, Ying-Hwa Kuo, Sergey Sokolovskiy, et al, 2004. The ROCSAT-3/COSMIC Mission and Applications of GPS Radio Occultation Data to Weather and Climate[J]. Remote Sensing Applications of the Global Positioning System, 5661: 1-12. DOI:10.1117/12.566544 |
Kuo Y-H, Sokolovskiy S, Anthes R A, et al. Assimilation of GPS radio occultation data for numerical weather prediction[J]. Special issue of Terrestrial, Atmospheric and Oceanic Science, 11(1): 157-186, March 2000. http://adsabs.harvard.edu/abs/2001acos.conf..157K
|
Syndergaard S. Retrieval Analysis and Methodologies in Atmospheric Limb Sounding Using the GNSS Occultation Technique[R]. DMI Scientic Report, Danish Meteorological Institute, Copenhagen, Denmark, 1996(6):49-52.
|
Syndergaard S, 1998. Modeling of the effect of the Earth's oblateness on the retrieval of temperature and pressure profile from limb sounding[J]. J Atmos Solar-Terr Phys, 60: 171-180. DOI:10.1016/S1364-6826(97)00056-4 |
陶士伟, 郝民, 薛纪善, 等, 2008. 数值预报同化系统中观测资料误差分析[J]. 气象, 34(7): 34-40. DOI:10.7519/j.issn.1000-0526.2008.07.006 |
岳迎春, 胡友健, 赵雪莲, 2007. 利用GPS无线电掩星技术探测大气的探讨[J]. 地理空间信息, 5(6): 36-38. |
Lei J, S Syndergaard, A G Burns. Comparison of COSMIC ionospheric measurements with ground-based observations and model predictions:preliminary results[J]. Journal of Geophysical Research, 112:A07308, doi:10.1029/2006JA012240, 2007. http://adsabs.harvard.edu/abs/2007JGRA..112.7308L
|
郭鹏, 严豪健, 黄珹, 等, 2006. 上海天文台CHAMP掩星资料处理结果的统计分析[J]. 天文学报, 4.47(2): 92-201. |
Kuo Y H, W S Schreiner, J Wang, et al. Comparison of GPS radio occultation sounding with radiosondes[J]. Geophysical Research Letters, 32, L05817, doi:10.1029/2004GL021443, 2005. http://adsabs.harvard.edu/abs/2005GeoRL..3205817K
|
曹云昌, 方宗义, 夏青, 等, 2006. 中国地基GPS气象应用站网建设展望[J]. 气象, 32(11): 42-47. DOI:10.3969/j.issn.1000-0526.2006.11.007 |
 2013, Vol. 36
2013, Vol. 36 