2. 国家环境预报中心,马里兰州, 美国
2. National Centers for Environmental Prediction, Maryland, U.S.A
在过去的10年中,人们发现基于全球模式的集合预报对中尺度概率预报是十分有效的。集合预报作为一种估计天气预报的不确定和制作概率预报的技术近年来得到了很大的进步[1-2]。但是,因为模式和集合方法的缺陷的影响,集合预报目前仍然存在不足之处。Toth等指出[3],模式的系统性误差一直存在,并且会引起集合预报一阶和二阶偏差。模式误差是预报偏差的主要来源之一。经过长期积分模式误差会趋向于模式内在的统计平衡状态,出现系统偏差。虽然正面改进模式各个环节来发展模式非常重要,但模式终究不能达到完美,总存在一些我们未知的不足,甚至即使能够意识到不足之处,现阶段也未必有办法解决。因此,发展经验性方法来减小模式误差对预报的影响是非常必要的。它能在现有模式的基础上改善预报结果,不失为一条提高预报能力的捷径。
另外,进行多模式集合研究存在一个主要的问题就是,因为所选取的模式、物理过程参数化方案的不同,使得每个集合成员的系统性偏差的差别很大,有悖于“成员等同性”的原则。这就要求我们先对多模式、多初值、多物理过程参数化方案的超级集合预报结果采用系统性偏差订正的方法扣除自身的系统性偏差,然后才能构造合理有效的多模式超级集合预报。
为了建立一个更好的中尺度预报系统,在集合预报产品使用之前完善后处理算法,去除系统性误差十分必要。所以研究和发展一套统计后处理方案,用以减小集合预报产品相对于分析场的系统性误差很有必要。1998年魏文秀等[4]用卡尔曼滤波技术对500 hPa高度场进行了订正试验,证明卡尔曼滤波双因子订正对提高暴雨预报能力是有效的;杨松等[5]用根据误差的特性,根据不同的物理量建立回归模型,去除模式的随机误差,取得了较好的效果;马清等[6]使用自适应误差订正方法对国家气象中心、日本气象厅、美国国家环境预报中心等多国的区域集合预报模式2 m温度预报做订正,订正后的各项检验指标都得到了不同程度的改善。递减平均方法是统计后处理方法中的一种,是一种自适应方法,该方法已经用于NCEP业务集合预报系统。本文将详细介绍这种方法的原理,并且对使用这种方法对集合预报产品一阶偏差进行估计和订正的效果评估。
1 偏差订正的原理和方法递减平均方法是一种自适应(卡尔曼滤波类型)偏差订正方法。卡尔曼滤波广泛应用在气象研究领域中,陈雷等[7]使用卡尔曼滤波方法对短期气候预测进行了研究和应用,梁钰等[8]使用卡尔曼滤波方法制作河南省沙尘短期预报。这种方法已用于美国国家环境预报中心业务集合预报系统,是在整个模式积分完成后进行的,通过计算滞后平均估算模式系统性偏差,然后对模式的预报结果进行订正处理[9]。自适应偏差订正方法是一种统计估算方法,通过处理一系列带有误差的实际测量数据得到所需要物理参数的最佳估算值。本文将详细介绍一阶偏差订正的方法和原理。其原理如下:
| ${{B}_{i,j}}(t)=(1-w){{B}_{i,j}}(t-1)+w\times ({{f}_{i,j}}-{{a}_{i,j}})$ | (1) |
式中Bi, j(t)表示当日12 UTC的任意一个格点(i, j)的一阶偏差订正值,Bi, j(t-1) 表示前一日12 UTC格点(i, j)的一阶偏差订正值,w表示权重系数,ai, j表示模式当日12 UTC格点(i, j)的分析值,fi, j表示对应分析值ai, j格点(i, j)的预报值,式中w决定了近期多长时间段的样本将对当天的预报订正产生影响,不同的w对应不同的权重变化曲线(图略),对于不同的w,曲线衰减速度是不同的,w越大,衰减越快;另外,对不同的w,同一天的样本资料对递减平均偏差的影响是不同的。w越大,临近日期的样本所占的权重越大,距离订正日期时间较长的样本所占的权重越小;反之亦然。模式的不同网格点、不同的预报时次、不同的物理量以及不同的天数都对应不同的递减平均偏差。
试验中分别对不同的w(1%、2%和10%)进行了效果检验,总体来说,w为2%的试验中对大部分地区和季节来说效果好于1%和10%的。因此,在以下的研究工作中,w的数值为2%。偏差估计和订正的步骤如下:
(1) 当t=1时实施“冷启动”,即Bi, j(t-1)=0;
(2) 然后,给定适当的权重,按照公式(1) 计算滞后平均Bi, j(t);
(3) 重复(2) 步骤,经过一段时间(大约为2个月)的迭代累加之后,得到的误差已经趋于稳定并能在一定程度上表征系统误差的情况;
(4) 在每个集合成员预报上扣除当下时次的误差,得到订正后的预报结果。
2 全球集合预报业务及检验方法 2.1 全球集合预报业务系统概述2004年初,中国气象局国家气象中心数值室开展了基于增长模繁殖扰动法产生初值的,建立在全球T213L31模式基础上的全球集合预报系统的研究。通过方案的制定实施和试验,2005年底,T213L31全球集合预报的核心技术问题得到解决,在IBM-sp高性能计算机上,建立了基于增长模繁殖法的我国T213高分辨率数值集合预报系统,解决了增长模繁殖法中的关键技术rescaling在全球谱模式的应用,“全球集合预报系统”开始在IBM的SP机上投入实时运行,从2006年4月开始在国家气象中心业务化运行,进行滚动预报,每天在00、06、12、18 UTC进行同化,在12 UTC制作1次10天预报,建立了7对扰动成员加控制预报共15个成员的集合预报系统。
2.2 集合预报检验方法简介为了全面分析预报系统的预报能力,本文拟采用多种检验评价方法,这些方法各有侧重,例如距平相关系数和均方根误差(类似的还有绝对误差和相对误差)侧重于确定性预报较多的分析检验;Talagrand分布侧重于集合概率预报的可靠性。下面给出这几种集合预报检验方法的原理和分析方案。
(1) 均方根误差、绝对误差和距平相关系数
均方根误差、绝对误差和距平相关系数同样是对集合平均进行常规检验的统计检验量。使用集合预报所有成员的集合平均和分析场(观测场)进行对比检验,计算均方根误差、绝对误差和距平相关系数(公式略),其计算方法和控制预报的求算方法相同。
(2) Talagrand分布
本方法是度量系统可靠性的方法之一。根据集合预报的原理,在统计学意义上,系统中每个成员的出现是等概率的。那么如果在由k个成员按非降序排列后构成的k+1个区间(包括两侧的开区间)中,实况值落在上述每个区间的概率是相等的。基于这一思想,Talagrand等[11]构造了一种直方图,用实况值落在上述每个区间的时空累积频率来描述集合预报系统可靠性,一般称之为Talagrand分布。具体的分析方法如下:对于某个区域(其中的格点数为P)有k个成员的T次集合预报结果(有效样本数为N=P×T),在第j(j=1,2,…,k+1) 个区间内,实况值落在该区间频数为Fj,其期望值为N/(k+1),那么实测值落在每个区间的概率分布为:
| ${{P}_{j}}=\frac{{{F}_{j}}}{N}$ | (2) |
Talagrand分布中直方图的形态可以反映预报系统可靠性方面的信息。使用本方法的大量分析表明集合预报成员间发散度不够,这是目前集合预报的普遍问题。
(3) 对全球集合预报偏差订正及结果检验分析
使用上文所介绍的递减平均方法对T213全球集合预报高层形势场和地面要素2 m温度预报进行了一阶偏差订正。对于高层形势场的检验,选择2006年5—8月500 hPa高度场和850 hPa温度场同其对应的分析场进行对比检验分析。由于我们更加关注全球集合预报产品对中期时效形势场的预报效果,因此本文中将重点分析全球T213集合预报形势场预报的第4~7天集合预报效果。统计检验量选择Talagrand分布、绝对误差和距平相关系数。对地面要素2 m温度选择2007年11月至2008年2月同地面观测进行检验对比分析,统计检验量选择均方根误差、相对误差、Talagrand分布和BS评分。
2.3 500 hPa高度场和850 hPa温度场订正前后的统计检验分析对2006年5—8月期间500 hPa高度场和850 hPa温度场使用对应的分析场进行一阶偏差订正,下面将分别从订正前后的Talagrand分布情况、绝对误差和距平相关系数等统计检验参数比较订正前后的效果。
(1) Talagrand分布
Talagrand分布检验是为了考察集合预报系统各成员的等同性及离散度,T213全球集合系统在理想的情况下的平均概率应该是6.25%。
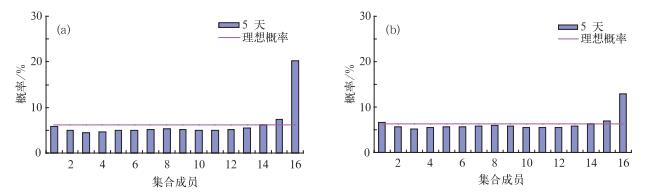
图 1是2006年8月T213集合预报500 hPa高度场赤道以北地区第5天预报订正前后的Talagrand分布情况,从图中可以看出,订正前“真值”落在最大预报值外的概率明显大于理想概率,说明系统存在一定的冷偏差;对照订正后的Talagrand分布可以看到,订正后的冷偏差明显减小,“真值”落在最大预报值外的概率由20.1%减小到13%,其他区间的预报概率均比订正前更加接近理想概率,这说明各个集合成员的预报等同性和“冷偏差”现象得到了改善。另外,需要说明的是,目前由于集合预报扰动方法和控制预报水平的原因,使得集合预报的离散度不够,Talagrand分布经常呈现“U”型分布,这种现象不仅存在于我国的集合预报系统,发达国家包括欧洲中心的集合预报系统同样存在这种问题。
|
图 1 2006年8月T213集合预报500 hPa高度场第5天预报订正前(a)和订正后(b)的Talagrand分布 Fig. 1 Talagrand distributions of No.5 day forecast for T213 EPS 500 hPa geopotential height before (a) and after (b) calibration August 2006 |
除了以上的分析以外,对2006年8月业务集合预报赤道以北地区500 hPa高度场第4、6和7天预报订正前后的Talagrand分布和理想概率进行对比分析。表 1是2006年8月T213集合预报赤道以北地区500 hPa高度场订正前后的预报概率和理想预报概率的偏差,从表中可以看到:订正后的概率偏差绝对值都比订正前减小,概率偏差相对值除了第一区间外也都是减小的,这就表明订正后各个集合成员的预报等同性都较订正前更好,比订正前更加接近理想概率。另外,还可以看到,第16区间的偏差在订正前远远大于其他区间,这说明系统存在明显的冷偏差,订正后冷偏差的情况得到了不同程度的改善,其概率分布更加接近理想概率,尤其是96小时预报,概率偏差由订正前的16.0减小为订正后的5.6,改善效果十分显著。
|
|
表 1 2006年8月T213集合预报赤道以北地区500 hPa高度场第4、6和7天的预报概率和理想预报概率的偏差 Table 1 Bias between T213 EPS 500 hPa geopotential height forecast and ideal probability of No.4, 6 and 7 day to the north of the tropic at August 2006 |
以上分析说明订正后500 hPa高度场Talagrand分布集合预报对于中期预报明显优于订正前的集合预报系统。
图 2是2006年8月T213集合预报赤道以北地区850 hPa温度场第5天预报订正前后的Talagrand分布情况,从图中可以看出,850 hPa温度场的集合预报同样存在冷偏差,即温度预报偏低;对照订正后的Talagrand分布可以看到,订正后的冷偏差明显减小,“真值”落在最大预报值外的概率由26%减小到14%,除了第一区间的预报概率订正后有所增大,其他区间的预报概率比订正前更加接近理想概率,这说明各个集合成员预报等同性和“冷偏差”现象都得到了改善。

|
图 2 2006年8月T213集合预报850 hPa温度场第5天预报订正前(a)和订正后(b)的Talagrand分布 Fig. 2 Talagrand distributions of No.5 day forecast for T213 EPS 850 hPa temperature before (a) and after (b) calibration at August 2006 |
同样,对2006年8月T213集合预报系统赤道以北地区850 hPa高度场第4、6和7天预报订正前后的Talagrand分布和理想概率的比较进行对比分析。表 2是850 hPa温度场第4、6和7天的预报概率和理想预报概率的偏差分布情况,从表中可以看到,除了第1和第14个区间订正后的概率偏差绝对值比订正前增大,其他14个区间订正后的概率偏差值无论是其绝对值和相对值都比订正前减小,这说明,对850 hPa温度场订正后的绝大部分集合成员的预报等同性都较订正前更好,比订正前更加接近理想概率。同500 hPa高度场相似的情况是,850 hPa温度预报存在比较明显的冷偏差,订正后第16区间的概率偏差明显减小,分别由原来的19.6、20.0和19.8减小到7.7、7.9和7.7,改善效果十分显著。
|
|
表 2 2006年8月T213集合预报赤道以北地区850 hPa温度场第4~7天的预报概率和理想预报概率的偏差分布 Table 2 Bias between T213 EPS 850 hPa temperature forecast and ideal probability of No.4-7 day to the north of the tropic at August 2006 |
以上分析说明订正后850 hPa温度场Talagrand分布对中期的预报效果明显优于订正前的集合预报系统,但是在一定程度上增大了第1区间即“真值”落在最小预报值内的预报概率。
(2) 绝对误差和距平相关系数统计
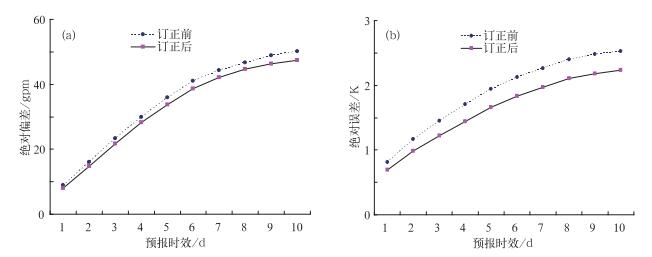
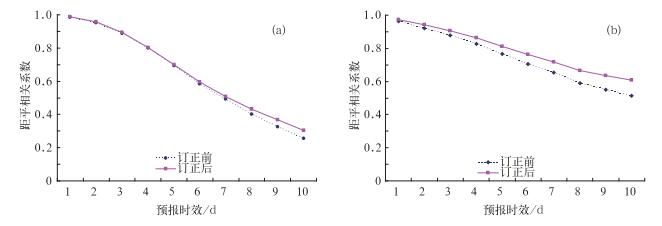
图 3和图 4分别是2006年8月T213集合预报500 hPa高度场和850 hPa温度场订正前后赤道以北地区的绝对误差和距平相关系数比较图。从图 3可以看到,500 hPa高度场和850 hPa温度场的1~10天的集合平均预报订正后的绝对误差都较订正前减小,随着预报时效的延长,订正后和订正前的绝对误差差距增大,这说明使用这种方法对中期天气预报的改善效果比短期天气预报更加显著。从图 4可以看到,500 hPa高度场和850 hPa温度场的1~10天预报订正后的距平相关系数都较订正前增大,而且随着预报时效的延长,订正后和订正前的距平相关系数差距越大,同样说明,使用递减平均方法做短期和中期天气预报均有改善,对中期预报的改善效果更明显。
|
图 3 2008年2月份T213集合预报赤道以北地区绝对误差 (a) 500 hPa高度场(单位:gpm); (b) 850 hPa温度场(单位:K) Fig. 3 Absolute errors of T213 EPS before and after calibration to the north of the tropic at February 2008 (a) 500 hPa geopotential height in gpm, (b) 850 hPa temperature in K |
|
图 4 2008年2月份T213集合预报赤道以北地区距平相关系数 (a) 500 hPa高度场; (b) 850 hPa温度场 Fig. 4 Anomaly correlation coefficients of T213 EPS before and after calibration to the north of the tropic at February 2008 (a) 500 hPa geopotential height in gpm, (b) 850 hPa temperature in K |
对于2米温度的集合预报,由于其地面分析场本身就存在较大的系统性偏差,因此使用加密观测场对其进行一阶偏差订正,取得了令人满意的效果。下面将分别从订正前后的绝对误差和均方根误差等统计检验参数比较订正前后的效果。
(1) 观测资料使用情况
本文选取2076个来报情况比较稳定的观测站对T213集合预报2 m温度的预报进行偏差订正及效果检验,观测和预报的时次是12 UTC。
(2) 均方根误差(RMSE)和相对误差(ME)
均方根误差和相对误差的计算方法如公式(3) 和公式(4),Fi是i格点的预报值,AVi是i格点的分析值。
| $RMSE=[\frac{1}{N}\sum\limits_{i=1}^{N}{{{({{F}_{i}}-{{A}_{Vi}})}^{2}}{{]}^{\frac{1}{2}}}}$ | (3) |
| $M{{E}_{i}}={{F}_{i}}-{{A}_{Vi}}$ |
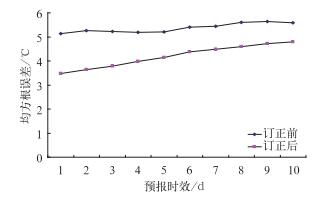
图 5是T213集合预报2 m温度预报订正前后均方根误差比较情况。从图中可以看到,1~10天预报订正后的均方根误差都较订正前减小,订正前各个预报时段的均方根误差变化不大,订正后随着预报时效的延长,均方根误差逐渐增大,这说明,订正后的T213集合预报2 m温度预报的误差比订正前减小,其对短期时效预报的改善效果相对优于对中期时效预报的改善效果。
|
图 5 2008年2月份T213集合预报2 m温度预报均方根误差(单位:℃) Fig. 5 RMS error (℃) of T213 EPS 2-m temperature at February 2008 |
为了更细致地检验对T213集合预报2 m温度预报的订正效果,除了对2076个站点的空间平均和2008年2月份29天的时间平均的误差情况进行统计分析以外,还对逐日单站的2 m温度集合平均预报的相对误差进行对比分析。通过对我国2008年2月份T213集合预报2 m温度集合平均的8个分区(东北地区、华北地区、西北地区东部、青藏高原中南部、新疆地区、长江中下游地区、西南地区东部和华南地区)的误差分析(图略),可以知道,东北地区、新疆地区、华北地区、西北地区东部和青藏高原中南部地区的相对误差以负误差为主,西南地区东部和长江中下游地区的相对误差在0 ℃附近变化,没有明显的正负误差,华南地区的相对误差以正误差为主。基于这3种误差分布情况,分别随机选取3个站点即北海站(59644)、武冈(57853) 和北京站(54511),对其进行逐日单站误差演变分析。
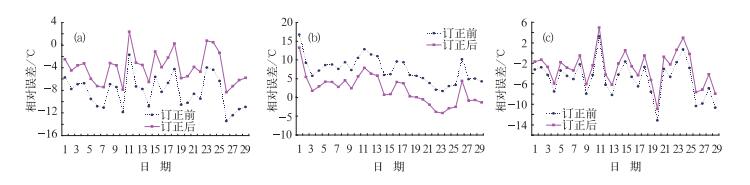
图 6a是北京站(54511)2008年2月份5天预报逐日相对误差演变图。从图中可以看到,订正前的相对误差都是负值,预报温度比观测偏低,相对误差的变化范围为-13.4~-1.72 ℃,说明预报存在明显的负系统性偏差;订正后相对误差情况得到了改善,相对误差的变化范围为-8.3~2.34 ℃,除了2月11日订正后的绝对误差比订正前相对有所增大以外,其余28天的系统性误差订正后都得到了改善。图 6b是北海站(59644)2008年2月份120小时预报逐日相对误差演变图。从图中可以看到,订正前的相对误差都是正值,预报温度比观测偏高,相对误差的变化范围为1.7~16.8 ℃,说明该站点的预报存在比较明显的正系统性误差;通过一阶偏差订正后,相对误差情况得到了改善,相对误差的变化范围是-4.2~13.3 ℃,除了2月22和23日订正后的绝对误差比订正前相对有所增大以外,其余27天的系统性误差订正后都得到了改善。图 6c是张北站(53399)2008年2月份120小时预报逐日相对误差演变图。从图中可以看到,订正前的温度预报比观测值明显偏低,27天的相对误差都是负值,该站点的预报存在显著的系统性误差,对其一阶偏差订正后,温度预报偏低的现象得到了有效改进,27天的预报订正后的误差绝对值小于订正前。
|
图 6 北京站(a)、北海站(b)和张北站(c)2008年2月逐日相对误差(单位:℃) Fig. 6 Relative errors of T213 EPS 2-m temperature at stations of (a) Beijing (54511), (b) Beihai (59644) and (c) Zhangbei (53399) at February 2008 |
(3) Talagrand分布
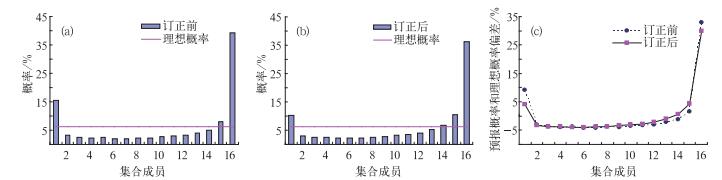
图 7是2008年2月T213集合预报2 m温度120小时预报Talagrand分布及预报概率和理想概率偏差。从图中可以看到,订正前第1区间和第16区间的预报概率高于理想概率,订正后的预报概率减小,比订正前接近理想概率。第2~8区间的预报概率订正前后相差不大,都是低于理想概率;第9~14区间预报概率,订正后比订正前更加接近理想概率;第15区间,订正后的效果是负效果。可以认为,订正后2 m温度集合预报中绝大多数成员的预报概率都比订正前更加接近理想概率,集合概率预报的可靠性得到了改善。
|
图 7 2008年2月T213集合预报2 m温度5天预报Talagrand分布及预报概率和理想概率偏差 (a)订正前; (b)订正后; (c)订正前后预报概率和理想概率偏差 Fig. 7 Talagrand distributions of No.5 day forecast for T213 EPS 2-m temperature before (a) and after (b) calibration, and bias (c) between forecast and ideal probability at February 2008 |
(1) 使用一阶偏差订正方法对T213集合预报的500 hPa高度场和850 hPa温度场进行系统性偏差订正,结果表明这种方法有效地减小了形势场预报集合平均的系统性误差,对形势场预报存在的“冷偏差”现象有明显的改善,提高了集合概率预报的可靠性。
(2) 使用加密观测站的观测数据对T213集合预报的2 m温度预报进行系统性偏差订正,结果表明:订正后集合预报的可靠性和分辨能力都较订正前有不同程度的改善;单站2 m温度预报偏高和偏低的现象通过一阶偏差订正,系统性误差明显减小;对系统性偏差不明显的站点,订正前后的差别不大,订正后大部分天数的误差绝对值较订正前减小。
(3) 在研究中还发现,使用这种偏差订正方法和权重系数的试验方案,对中期时段预报改善效果优于对短期时段预报的改善。
(4) 一阶偏差订正方法出现过个别的负面订正的效果,另外这种方法不能改变集合预报的离散度,在下一步工作中计划在一阶偏差订正的基础上开展二阶偏差订正,对集合预报的离散度展开订正。
| [1] |
杜钧, 陈静. 单一值预报向概率预报转变的基础:谈谈集合预报及其带来的变革[J]. 气象, 2010, 36(11): 1-11. DOI:10.7519/j.issn.1000-0526.2010.11.001 |
| [2] |
杜钧, 邓国. 单一值预报向概率预报转变的价值:谈谈概率预报的检验和应用[J]. 气象, 2010, 36(12): 10-18. DOI:10.7519/j.issn.1000-0526.2010.12.002 |
| [3] |
Zoltan Toth, Yuejian Zhu. The use of ensembles to identify forecasts with small and large uncertainty[J]. American Meteorological Society, 2001(August): 463-477. |
| [4] |
魏文秀, 仁彪, 杨海龙, 等. 卡尔曼滤波技术在暴雨中期预报中的应用[J]. 气象, 1998, 24(3): 46-49. DOI:10.7519/j.issn.1000-0526.1998.03.010 |
| [5] |
杨松, 杞明辉, 姚德宽. 误差订正在预报集成中的应用研究[J]. 气象, 2003, 29(12): 22-24. DOI:10.3969/j.issn.1000-0526.2003.12.005 |
| [6] |
马清, 龚建东, 李莉. 超级集合预报的误差订正与集成研究[J]. 气象, 2008, 34(3): 42-48. DOI:10.7519/j.issn.1000-0526.2008.03.007 |
| [7] |
陈雷, 刘开福, 李英. 卡尔曼滤波在短期气候预测中的应用[J]. 气象, 2001, 27(10): 42-46. DOI:10.3969/j.issn.1000-0526.2001.10.010 |
| [8] |
梁钰, 布亚林, 贺哲, 等. 用卡尔曼滤波制作河南省冬春季沙尘天气短期预报[J]. 气象, 2006, 32(1): 63-67. |
| [9] |
李莉, 朱跃建. T213降水预报订正系统的建立与研究[J]. 应用气象学报, 2006, 17(增刊): 130-133. |
| [10] |
Toth Z, O Talagrand, G Candille, et al.Probability and ensemble forecasts[M].in: Jolliffe I, D Stephenson. Forecast Verification:A practitioner's guide in atmospheric science.Wiley Press, 2003:137-163.
|
| [11] |
Talagrand O, Vautard R.Evaluation of probabilistic prediction systems[C]. Workshop on Predictability ECMWF, 1997-10.
|
| [12] |
陈朝平, 冯汉中, 陈静. 基于贝叶斯方法的四川暴雨集合概率预报产品释用[J]. 气象, 2010, 36(5): 32-39. DOI:10.7519/j.issn.1000-0526.2010.05.004 |
| [13] |
张利红, 杜钦, 陈静, 等. 地面观测资料在西南地区数值预报中的敏感性试验[J]. 气象, 2009, 35(6): 26-35. DOI:10.7519/j.issn.1000-0526.2009.06.004 |
 2013, Vol. 37
2013, Vol. 37 