2. 94514部队,济南 250002
2. Troops 94514 of PLA, Jinan 250002
多年来,很多人在相似预报方面做了大量的研究和探索[1-14],更有人将相似预报的思想引入到数值预报中。任宏利等[6]利用Lorenz模式开展了大量理论分析和数值试验,发现在初始状态相似性持续的情况下,动力预报结果及其预报误差行为具有相似性,进而提出动力预报的相似性原理:在初始状态相似性持续的情况下,基于某一模式的动力预报结果及其误差行为具有相似性。据此建立了一个相似-动力集合预报试验性系统,并实施了长达31个月的实时准业务月动力延伸预报试验,与同期国家气候中心的业务集合预报相比,显示出令人鼓舞的结果和非常好的业务应用前景。制作相似预报,除了要有好的方法、好的因子外,还要有适用的相似性度量,为此许多气象工作者对不同的相似性度量进行了预报检验。阎惠芳等[7]对常用相似性判据进行了降水预报检验,各相似量从优至劣排序为:相关系数、相似系数、欧氏距离、海明距离和相似离度[8];万日金等[9]的检验结果从优至劣排序为:海明距离、相似离度、欧氏距离、相似系数;陈磊等[10]的相似性测度对比分析结果为:灰关联度较好,其次为相关系数和相似系数,最差为欧氏距离和相似离度。目前,很多人在没有比较各相似性度量优劣的情况,会选用相似离度作为相似判据,因为它具有所谓的“形”、“值”判断能力,而上述的相似量研究结果表明事实并非如此。为了找到更好的相似量,一些人将相似系数或相关系数与所谓“值系数”(或称距离系数)相乘或相加,作为新的相似量[7, 11-12]。本文主要对相似离度、海明距离、相关系数等相似量的性质进行分析探讨,指出它们使用的局限性。
1 海明距离与相似离度的关系由于篇幅所限,以下仅对海明距离和相似离度进行分析。
1.1 海明距离如以Hij表示两样本间的海明距离,则其表达式为:
| $ {H_i}_j = \sum\limits_{k = 1}^m {\left| {{x_{ik}} - \left. {{x_{jk}}} \right|} \right.} $ | (1) |
式中,i、j表示两个样本,x表示因子数值,m表示因子数量,k表示因子序号(各符号意义下同)。Hij的值域为[0,N),N为一不定的数,当其为0时两样本最相似,N越大越不相似。而所谓的欧氏距离Oij(见公式2) 的表达式与海明距离相近,因此两者具有相同的性质。
| $ {O_{ij}} = \sqrt {\sum\limits_{k = 1}^m {{{\left( {{x_i}_k- {x_{jk}}} \right)}^2}} } $ | (2) |
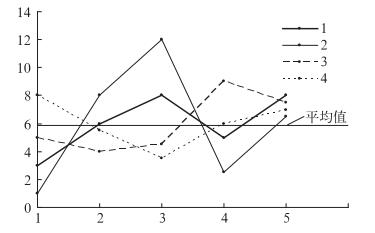
从海明距离的表达式可见,它反映的是两个样本的空间距离,而对形状差异反映不明显,而形状差异才是相似的关键。比如,从表 1中的4个样本(每个样本有5个因子,平均值相同为6) 及其在图 1中的对应曲线可以明显看出,样本1与样本2、样本3与样本4比较相似,但实际计算结果表明,样本1与样本2、3、4的海明距离是一样的,即
|
图 1 相似性比较示意图 Fig. 1 Sketch map of similarity contrast |
|
|
表 1 海明距离、相似离度与相似量R的对比分析 Table 1 Comparative analysis of Hammin distance, similarity parameter, similarity measurement R |
1986年,李开乐[8]提出了一个相似量——相似离度,认为可以反映样本的“形”与“值”,因此,目前使用者较多。但是,相似离度并不能真正地反映样本的“形”与“值”,它的相似选择能力与海明距离并无明显差异,后面将看到,相似离度实际上也是一种广义的海明距离;而阎惠芳等[7]、陈磊等[10]的相似预报试验表明,相似离度是各相似量中表现最差的。
如以Cij表示两样本i、j间的相似离度,则其表达式为:
| $ {C_{ij}} = \frac{1}{2}\left( {{S_{ij}} + {D_{ij}}} \right) $ | (3) |
式中,Sij即所谓的“形系数”,Dij即所谓的“值系数”,若以dk表示两样本i、j的第k个因子差,则
| $ {S_{ij}} = \frac{1}{m}\sum\limits_{k = 1}^m {\left| {{d_k} - {E_{ij}}} \right|} $ | (4) |
| $ {D_{ij}} = \frac{1}{m}\sum\limits_{k = 1}^m {\left| {{d_k}} \right|} $ | (5) |
| $ {d_k} = {x_{ik}} - {x_{jk}} $ | (6) |
| $ {E_{ij}} = \frac{1}{m}\sum\limits_{k = 1}^m {{d_k}} $ | (7) |
Cij的值域为[0,N),N为一不定的数,当其为0时两样本最相似,N越大越不相似。式中“值系数”Dij的“值”并不是前面提到的平均值,它反映的不是两样本平均值的差异程度。从式(5) 和(6) 可以看出,它实际上是两样本的海明距离对因子总数m求平均,不妨称其为“平均海明距离”,所以Dij反映的是两样本空间距离的大小,而这种距离是“形”与“值”共同影响造成的,因此,Dij并不是什么“值系数”。
Eij实际上是样本i与样本j的平均值的差,因为,若以M表示平均值,Eij可以用下式表示。
| $ {E_{ij}} = \frac{1}{m}\sum\limits_{k = 1}^m {{d_k}} = \frac{1}{m}\sum\limits_{k = 1}^m {\left( {{x_{ik}}- {x_{jk}}} \right) = {M_i}- {M_j}} $ | (8) |
将式(6) 和式(8) 代入式(4),则“形系数”Sij的另一种表达式为:
| $ \begin{array}{l} {S_{ij}} = \frac{1}{m}\sum\limits_{k = 1}^m {\left| {{d_k}- {E_{ij}}} \right|} = \\ \frac{1}{m}\sum\limits_{k = 1}^m {\left| {\left( {{x_{ik}} - {M_i}} \right) - \left( {{x_{ik}} - {M_j}} \right)} \right|} \end{array} $ | (9) |
可见,Sij实际上是“样本距平”的海明距离对因子总数m求平均,不妨称其为“平均距平海明距离”,因此,Sij也无法反映出“样本距平”的形状变化。
特别地,如果Mi=Mj,即两样本的平均值相等,则Eij=0,Sij=Dij,Cij蜕变为一个“平均海明距离”。所以,相似离度实际上是一种广义的海明距离。如图 1中的各条曲线,它们的平均值均为6,相似离度变为平均海明距离,Cij=Hij/5,分辨不出目标样本1与样本2、3、4间的相似差异。尤其重要的是,在相似样本的选择过程中,样本间的平均值往往很接近,因此,相似离度与海明距离的相似选择能力几乎没有什么区别。
1.3 相似量R下面给出罗阳提出的一个相似量[13],其表达式为:
| $ {R_{ij}} = 1 - \frac{{\sum\limits_{k = 1}^m {\left| {\left( {{x_{ik}} - {{\overline x }_i}} \right) - \left( {{x_{ik}} - {{\overline x }_j}} \right)} \right|} }}{{\sum\limits_{k = 1}^m {\left| {\left( {{x_{ik}} - {{\overline x }_i}} \right) + \left( {{x_{ik}} - {{\overline x }_j}} \right)} \right|} }} $ | (10) |
Rij的值域为[0,1],当其为1时两样本最相似。当Rij为0时,是不相似,而不是最不相似。因为当两样本每个因子的距平符号相反时,有
从表 1中可以看出,
为了更准确地比较相似量R、C和H的相似选择特性,将常用的相似系数S和相关系数r也加入到对比的试验中。试验样本为2010年5月1—30日共30天的08时东亚区域的850 hPa高度场,历史库为1999—2009年共11年的高空绘图报资料;参与相似量计算的资料为此区域内96个站点的高空绘图报资料;试验方法为,用本文提到的相似量R、C、H、S和r,逐日计算试验样本与历史资料的相似性,对每个相似量,取每日计算结果前10个相似性好个例日期进行对比分析。如果两个相似量选出的10个相似个例中,相同的日期多,说明这两个相似量功能相近,反之,说明这两个相似量差异较大。为了定量考察两个相似量相似选择结果的相同程度,引入一个相同率来表示,相同率即相同个例数占相同与不同个例数和的比率。对整个试验而言,两个相似量相同率的计算方法为,将每日的相同个例数进行30天的累加,然后除以总个例数300。以下将进行两两相似量的比较分析。
2.2 相同率分析用上面的试验方法,可得出两两相似量的相同率结果,见表 2。
|
|
表 2 相似量间的相同率分析 Table 2 Identical rate analysis of similarity measurements |
由表 2可知如下事实。
(1) 相似离度C与海明距离H相似选择能力非常接近,相同率达0.82,为最高,这与前面的分析是一致的。
(2) 相似离度C与相关系数r差异最明显,相同率只有0.25,为最低,与罗阳提出的相似量R相比,相同率为0.35,为次低。
(3) 相似量R与相关系数r比较接近,相同率为0.60。
由此可见,相似离度确实与海明距离接近,而且由于与相关系数差异大,说明选出的相似样本相关性不好,形状上可能不是很像。而相似量R与相关系数接近,说明选出的相似样本相关性较好。
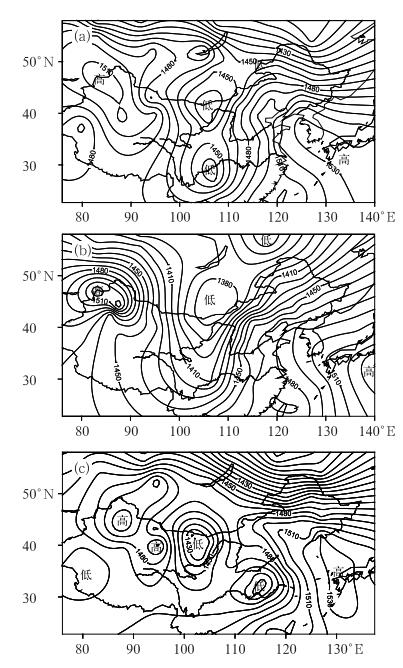
2.3 相似图分析本文对2010年5月16日08时的东亚850 hPa高度场进行了相似计算,相似量R与相关系数r找出的最相似日是2009年6月18日,相似离度C和海明距离H找出的最相似日是2006年5月25日。从图 2中可以看出,2009年6月18日的图与原图在形状上更为接近,但平均值要小于原图,这说明了相似量R与相关系数r主要从形状上选择相似;而2006年5月25日的图在“值”上与原图更为接近,这说明了相似离度C和海明距离H主要反映值的接近程度,即空间距离的大小,对形状的选择能力较弱。
|
图 2 850 hPa高度场对比分析 (a) 2010年5月16日08时;(b)相似量R、相关系数r找出的最相似日为2009年6月18日;(c)相似离度C、海明距离H找出的最相似日为2006年5月25日 Fig. 2 Comparative analysis of 850 hPa height fields (a) at 08:00 BT 16 May 2010, (b) the most similar day (18 June 2009) found out by using analog quantity R and correlation coefficient r, and (c) the most similar day (25 May 2006) found out by using similarity parameter C and Hamming distance H |
通过上面的分析讨论,可得到如下结论。
(1) 相似离度实际上是一种样本间“距离”的度量,并无所谓“形”、“值”系数的特性,它与海明距离、欧氏距离非常接近,它们只是反映两个样本的空间距离,无法准确反映形状和强度,尤其是当两个样本的平均值相同时,更是无法区分它们之间的差别。
(2) 相似量R与相关系数r的性质更为接近,它与样本的形状、强度有关,而与空间距离或者说平均值无关。
罗阳通过相似预报研究还发现,用某种相似量与反映平均值的量组成的综合相似系数,其相似选择能力有时并不好,因为有时高的平均值系数会掩盖低的形状系数,而预报员更关注形状的是否相像。所以,较好的方法应是,确定相似选择的时间窗口(即历史上相近的时间段),以保证样本平均值大体相同,然后用能反映形状、强度相似的相似量进行相似选择,这样就会选出平均值接近、形状相似的样本。在此基础上,如能加上有经验预报员的分析判断,就会进一步提高预报效果。
| [1] |
晁淑懿, 金荣花. 一种综合相似中期预报模型[J]. 应用气象学报, 1996, 7(3): 300-307. |
| [2] |
邵明轩, 刘还珠, 窦以文. 用非参数估计技术预报风的研究[J]. 应用气象学报, 2006, 17(增刊): 125-129. DOI:10.3969/j.issn.1001-7313.2006.01.013 |
| [3] |
张延亭, 单九生. 逐步引进因子场作相似预报[J]. 气象, 2000, 26(3): 22-27. DOI:10.3321/j.issn:1000-0534.2000.02.013 |
| [4] |
张丰启, 崔晶, 王仁胜. 相似离度在入型判别和定时、定点、定量预报中的应用[J]. 气象, 2002, 28(9): 44-48. DOI:10.7519/j.issn.1000-0526.2002.09.010 |
| [5] |
李博, 赵思雄, 陆汉城, 等. 综合多级相似预报技术在暴雨短期预报中的检验[J]. 应用气象学报, 2008, 19(3): 307-314. DOI:10.11898/1001-7313.20080306 |
| [6] |
任宏利, 丑纪范. 动力相似预报的策略和方法研究[J]. 中国科学D辑, 2007, 37(8): 356-364. |
| [7] |
阎惠芳, 李社宗, 黄跃青, 等. 常用相似性判据的检验和综合相似系数的使用[J]. 气象科技, 2003, 31(4): 211-215. |
| [8] |
李开乐. 相似离度及其使用技术[J]. 气象学报, 1986, 44(2): 174-183. DOI:10.11676/qxxb1986.024 |
| [9] |
万日金, 何溪澄, 林刚. 用动力相似方法预报广东省区域暴雨预报试验[J]. 热带气象学报, 2006, 22(2): 198-202. |
| [10] |
陈磊, 翟宇梅, 王力维. K近邻非参数回归技术常用相似性测度的对比分析[J]. 军事气象水文, 2010, 2: 24-27. |
| [11] |
单九生, 张延亭. 江西省流域降水客观预报方法简介[J]. 江西气象科技, 2001, 24(4): 9-13. |
| [12] |
郭达烽, 许爱华, 肖安. 多级相似作温度精细化预报初探[J]. 江西气象科技, 2005, 28(3): 23-26. |
| [13] |
罗阳. 一种新的相似性度量—高分辨相似系数[J]. 空军气象学院学报, 1996, 17(1): 23-32. |
| [14] |
龚振淞, 杨义文. 中国夏季旱涝气候预测相似模型[J]. 气象, 2010, 36(5): 46-50. DOI:10.7519/j.issn.1000-0526.2010.05.006 |
 2011, Vol. 37
2011, Vol. 37 