2. 丰都县气象局, 重庆 408200;
3. 南京信息工程大学应用气象学院,南京 210044
2. Fengdu Meteorological Office, Chongqing 408200;
3. Department of Applied Meteorology, Nanjing University of Information Science and Technology, Nanjing 210044
我国三峡库区地处大巴山褶皱带、川东平行岭谷和川鄂湘黔隆起褶皱带三大构造单元的交汇处,北靠大巴山,南依云贵高原,位于长江中上游两大火炉——重庆和武汉之间。近年来,高温干旱等极端天气事件频繁发生,分析三峡库区高温自然振荡性质,预测未来趋势具有十分重要的现实意义。
气候系统是非线性复杂系统,气候序列具有明显的非线性/非平稳性、层次性,许多大小不一的时、空尺度构成了多层次结构。研究表明[1-4],气候系统的多层次结构正是导致其非平稳行为的重要原因之一,一个气候态可以由低层次向高层次转化,这个状态的改变通常称为“突变”,这是非平稳性的集中体现。以往对非平稳数据的分析研究多采用Fourier变换、Winger分布、小波变换等[5-6],但它们大都以傅里叶变换为最终的理论依据,采用它们分析非平稳数据容易产生虚假频率等现象,或者得到的结果没有清晰的物理含义。
Huang等[4]于1998年提出一种新的分析非平稳、非线性数据的时频分析方法—经验模态分解(empirical mode decomposition,EMD)方法。该方法被认为是近年来对以傅里叶变换为基础的线性和稳态谱分析的一个重大突破。由于时间序列的信号经过经验模态分解,即逐级进行平稳化处理,把不同周期的波动从原信号中分离出来,并且该波动是平稳的,最后得到的是趋势分量,不同尺度的波动被定义成为本征模态函数(Intrinsic Mode Function, IMF),IMF波动分量具有显著的缓变波包的特性,而趋势分量则是单调函数或者均值函数;不同的IMF分量是平稳信号,具有非线性特征,其缓变波包特征意味着不同特征尺度波动的波幅随时间变化,因而也具有时间上的局域化特征;对IMF分量进行Hilbert变换得到Hilbert谱,它能反映原动力系统的真实物理过程,提供了更加清晰详细的局部细节特征[7]。近年来,EMD方法及相应的Hilbert变换正成为处理非线性/非平稳时间序列的有力手段,已经成功应用于大气科学等研究领域[8-11]。
由于气候观测序列普遍具有层次性、非线性和非平稳性,这给建立预测方法带来了极大困难,气候预测仍然是世界性的难题,在目前数值预报能力有限的情况下,许多学者探索了非线性建模的预测方法,如陈永义[12]将支持向量机(support vector machines, SVM)方法引入到气象领域;万仕全等[1]做了基本EMD方法的观测数据信息提取与预测研究,魏凤英等[13]研究了大气环流降尺度因子在中国东部夏季降水预测中的作用。本文试图在EMD和现有预测方法的基础上构建一个新的预测模型,模型包含EMD、均生函数(mean generate function,MGF)模型和神经网络模型(BP),其中MGF和BP神经网络已发展成熟,应用较广泛[14-15],尝试将此新模型应用于三峡库区高温气候诊断预测分析的方法性研究。
1 资料与方法所用资料由重庆市气候中心与湖北省气候中心提供,在综合考虑站点数据的时间序列长度、完整性和代表性的基础上,选择分布于三峡库区附近35个气象站,其中宜昌、秭归、巴东、巫山、奉节、云阳、万州、忠县、丰都、涪陵、长寿、武隆、彭水、沙坪坝、巴南和江津16个站为沿江站,自三峡水库宜昌库首向西沿江分布(图 1),其余站点为三峡库区周边站;时间是从1961年1月1日到2008年12月31日连续48年的观测数据,用于三峡库区高温的分析研究。
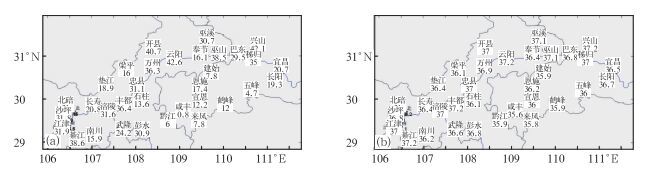
|
图 1 三峡库区年平均高温日数(a)和高温日平均最高气温分布(b) Fig. 1 Distribution of mean annual high temperature days (a) and mean daily highest temperature during annual high temperature days (b) in the Three Gorges area |
日最高气温≥35℃可作为炎热程度的指标[16],中国气象局规定这样的天气为高温天气。本文以三峡库区35站历年高温资料为样本,以日最高气温≥35℃为指标,建立各站历年高温日数和高温日平均最高气温序列,探讨三峡库区高温天气的气候特征,并对未来三峡库区高温日数和高温日平均最高气温进行预测。
采用Huang等提出的经验模态分解(EMD)方法, 从三峡库区高温日数与高温日平均最高气温序列中逐级分离出本征模态函数(IMF)分量, 通过分析这些分量揭示原序列内在的多尺度振荡变化。分离的方法是采用筛选过程:把序列中的极大值和极小值分别用(3次)样条函数曲线连结起来,构成上、下两条包络线,它们的均值线为m1。由原序列X(t)与m1之差得到h1:经过k次筛选, 使得h1的全部极大值都为正, 极小值都为负, 并且局部峰和谷的波形关于横轴(零均值线)是基本对称的。这样得到了第一个本征模态函数IMF1 :
| ${C_1}\left( t \right) = {h_{1k}}\left( t \right) = {h_{1(k - 1)}}\left( t \right) - {m_{1k}}\left( t \right)$ | (1) |
式中C1是原序列中时间尺度最短即最高频的分量(模态)。然后把C1从原序列中分离出来, 得到剩余序列r1, 再对r1重复上述过程, 得到第二个IMF分量C2。如此进行下去, 原序列就可用逐级分离出的IMF分量表示:
| $X\left( t \right) = \sum\limits_{i = 1}^n {{C_i}\left( t \right) + {r_n}\left( t \right)} $ | (2) |
其中rn是最后的“剩余”, 即趋势项, 它可以表示整个序列的总趋势。停止筛选过程所用的门限值SD是每次筛选前后的序列之差:
| $\begin{gathered} SD = \sum\limits_{t = 0}^T {\left[ {\frac{{{{\left| {{h_{j(k - 1)}}\left( t \right) - {h_{jk}}\left( t \right)} \right|}^2}}}{{h_{j(k - 1)}^2\left( t \right)}}} \right]} \hfill \\ \quad \quad j = 1, \cdots ,n;{\text{ }}k = 1,2, \cdots , \hfill \\ \end{gathered} $ | (3) |
式中SD实际上是筛选的精度, 在本文中, 针对三峡库区高温日数与高温日平均最高气温序列的具体数值变化, 分别经过试验确定门限取值。
式(2) 表明, 原序列X(t)可被分解为有限的n个IMF分量(Ci,i=1,…,n)之和以及1个趋势项rn。每一个分量表征原序列内在的一种时间尺度的振荡, 它的非平稳性减弱了, 原序列的非平稳性主要包涵在非零的趋势项中。因此, EMD方法适合于分析非平稳序列中的振荡模态。
2 三峡库区高温气候特征 2.1 三峡库区高温空间分布三峡库区及其周边地区山多,丘陵、盆地、河谷交错其间,由于特殊的地理位置,使得高温日数空间分布差异明显。由1961—2008年三峡库区高温日数分布图可见(图 1a),西部的江津、沙坪坝、北培、綦江和库区中部彭水、涪陵、奉都、忠县、万州以及库区东部的巫山、巫溪、巴东、秭归三个地带年平均高温日数较多,一般在30~42 d/a;库区东南部及奉节、垫江、梁平等海拔较高地区年高温日数较少,在20 d/a以下,其中来风、建始、黔江等年平均高温日数不足10 d/a,咸丰最少,仅有0.8 d/a。总体来看,三峡库区高温日数的分布基本上呈现峡谷多、山区和丘陵少,库区北部多、南部少的分布特点,与叶殿秀等[17]计算的1961—2002年三峡库区高温日数空间分布特点相一致,但高温日数偏多,其中沿江站平均偏多0.7 d/a,周边站偏多0.4 d/a。
高温日平均最高气温以库区东南部较低,东北部较高(图 1b)。在48年间,三峡库区有10个站高温日平均最高气温超过37.0℃,其中兴山、綦江高温日平均最高气温最高,为37.2℃。有7站高温日平均最高气温低于36.0℃,主要集中在库区东南部,其中咸丰站最低,为35.6℃。
图 2为三峡库区各站1961—2008年高温日数的趋势系数,可见趋势系数基本呈现出两头减少,中间略增多的分布格局。库区东部秭归呈显著的降低趋势,趋势系数为-0.49,通过了0.05的显著性检验。库区西部降低区域为忠县以西一带,幅度较小,没有通过0.05显著性检验;增加区域主要集中在开县、万州至五峰、黔江一带,经检验,趋势变化均不显著。
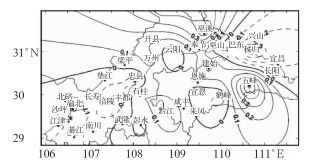
|
图 2 三峡库区年高温日数趋势系数的空间分布 Fig. 2 Trend coefficient in the spatial distribution of mean annual high temperature days in the Three Gorges area |
表 1为1961—2008年期间三峡库区35个站高温日数与35个站的平均高温日数之间的相关系数,可见相关系数均在0.6以上(除五峰、巫溪和秭归外),远远超过0.001显著性水平检验(R0.001=0.46),有28个台站(占80%)的相关系数在0.8以上,其中有16个台站(占46%)的相关系数在0.90以上。35个站高温日平均最高气温与35个站的平均高温日平均最高气温之间的相关系数均在0.82以上(表略),说明三峡库区高温变化趋势相当一致,35个站平均的高温日数、高温日平均最高气温能够很好地反映该地区高温的时间演变情况。
|
|
表 1 1961—2008年三峡库区35个测站高温日数与平均高温日数的相关系数 Table 1 The correlations between the high temperature days at each of 35 station in the Three Gorges area and the mean of the high temperature days from 1961 to 2008 |
图 3a为三峡库区1961—2008年高温日数和高温日平均最高气温的逐年变化曲线。由图可见,48年平均每年有24.07 d是高温天气,三峡库区高温日数总体呈先下降后上升的变化趋势,20世纪60年代到70年代高温日数经历了几次小的波动,总体偏多(60年代平均为25.55 d,70年代平均为26.76 d);进入80年代呈下降趋势,80年代高温日数偏少(80年代平均17.77 d),1980—1989年这10年期间只有3年的高温日数在48年平均值以上, 1987年平均高温日数只有8.94 d,为48年的最小值;90年代高温日数开始有所增加(90年代平均24.11 d);进入21世纪,受2006年夏季高温异常的影响(49.09 d),三峡库区高温日数增加迅速,2001—2008年平均每年有26.58 d高温天气。
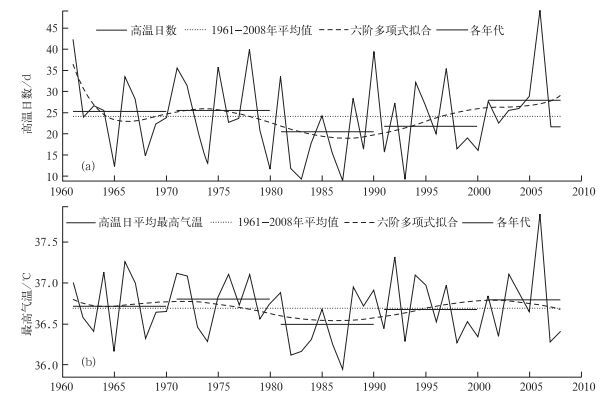
|
图 3 1961—2008年三峡库区年平均高温日数(a)和高温日平均最高气温(b)的变化曲线 Fig. 3 The time change curve of the high temperature days (a) and mean daily highest temperature during annual high temperature days (b) of the Three Gorges area from 1961 to 2008 |
以1971—2000年三峡库区高温日数22.62 d和高温日平均最高气温36.69℃为常年值, 分析了1961—2008年每10年间(其中2001—2008年为8年间)三峡库区高温的年代际距平。统计结果表明,各年代三峡库区高温日数和高温日平均最高气温呈现出一致的变化趋势。在20世纪80、90年代,高温日数和高温日平均最高气温都为弱负距平(距平值分别为-2.05、0.81 d和-0.19、-0.01℃)外,在其他时期,高温日数和高温日平均最高气温都为正距平。在21世纪的8年间, 高温日数和高温日平均最高气温正距平最高,距平值分别为5.28 d和0.10℃,其次是20世纪70年代,距平值分别为2.95 d和0.11℃。
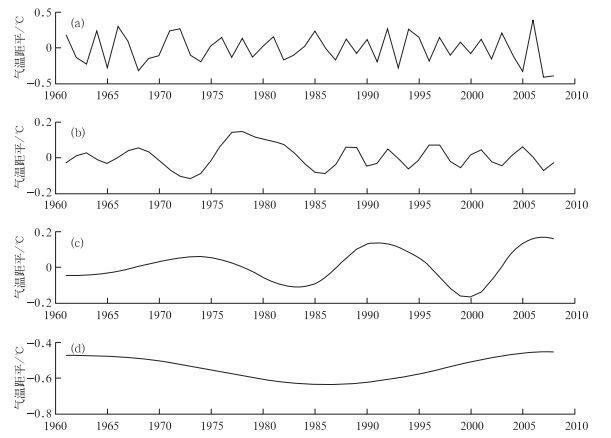
3 基于EMD方法的数据信息提取与预测 3.1 三峡库区高温变化的振荡模态结构采用EMD方法对1961—2008三峡库区年平均高温日数序列进行逐级分解,结果如图 4和表 2所示。为了避免产生边际效应,在EMD分解前将原资料序列进行了对称性延拓[5]。图 4给出了5个IMF分量(IMF1~IMF5对应图 4a~4d)和一个趋势项(图 4e),纵坐标值是气温距平的变化数值,表征高温日数振荡的幅度振幅或能量(振幅的平方)。表 2为每个分量的方差贡献率。各IMF分量表示不同尺度的变化,每一个IMF分量只是一个窄波段的信号;虽然一个IMF分量可能包含不同尺度变化的信息,但同一个时间段、不同IMF分量却不会包含同一个尺度的波动信号。
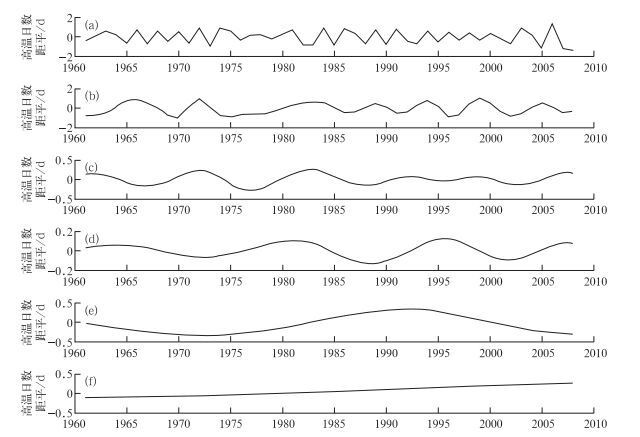
|
图 4 1961—2008年三峡库区高温日数的IMF1~5分量(a~e)和1个趋势项(f) Fig. 4 IMF components (a-e) and tendency change (f) of the high temperature days in the Three Gorges area from 1961 to 2008 |
|
|
表 2 三峡库区高温日数与高温日平均最高气温各IMF的周期和方差贡献率 Table 2 Period and variance contribution ratio of each IMF component of the high temperature days and mean daily highest temperature during annual high temperature days in the Three Gorges area |
Huang等[4]指出,每个IMF分量可能对应某一物理背景,IMF通过Hilbert变换得到Hilbert谱,谱结构的特征就可进一步揭示隐藏在时间序列中特定的物理过程。因此,找出气候序列中的关键IMF分量有重要的气候预测意义。分析这5个IMF分量,IMF 1表示一个3~4年尺度的振荡,IMF 2表示大约6年左右的气候变率,表明库区高温日数的年际变化比较复杂;IMF 3表示约10~12年的波动,IMF 4表示尺度约16年左右的变率,表现了1961—2008年期间库区高温日数由多到少的3波长时间变化,清楚地反映了近50年来三峡库区高温日数的年代际趋势;分别在1965、1981、1997和2006年为波峰,1973、1988和2002年为波谷。IMF 5表示34年以上的气候波动。趋势项(图 4f)是单调上升的直线,表明原序列有明显的非平稳性,而且近50年来三峡库区高温日数是总体上升的趋势,大约0.18d/10a。对单个IMF分量的考察,可以分析各种周期分量在气候变化中的可能作用。图 4中,IMF 4清晰地显现出20世纪80年代高温日数为负距平,2002年以后高温日数为正距平。IMF 3也表明80年代高温日数明显小于多年平均值,2002年后出现一个明显的气候波动的上升相位。可见,三峡库区高温日数80年代偏少和2002年以后偏多,气候的周期性变化贡献较大,主要受16年左右的气候周期性变率的影响。由各IMF方差贡献率(表 2)可以看出,原序列的变化主要是由IMF1、IMF2和IMF4这3个本征模态构成的,它们分别反映了3~6年、12年、16年左右时间尺度的振荡变化。
图 5是近48年来三峡库区高温日平均最高气温的EMD分解的4个IMF分量(图 5a~d)。IMF 1表示一个3年左右尺度的振荡,IMF 2表示在20世纪80年代中期以前约8年左右、1985—2008年约5年左右的气候变率,IMF 3表示约16年的波动,表现出1961—2008年内的低→高→低→高→低→高的长时间变化,把近50年来三峡库区高温日平均最高气温的大体走势表现得很清楚。趋势项(图 4f)是三阶趋势线,表明原序列有明显的非平稳性,三峡库区高温日平均最高气温从20世纪60年代中期到80年代中期呈下降趋势,80年代中期后,呈上升趋势。由各IMF方差贡献率(表 2)并结合图 5可以看出:在3个分量中,高频分量IMF1和IMF2振幅较大,说明高温日平均最高气温的年际变化很明显,是造成原序列涨落的主要原因,表明三峡库区高温日平均最高气温以3~5年、16年左右周期的振荡为主;分量IMF3适合于分析年代际变化。
|
图 5 1961—2008年三峡库区高温日平均最高气温的IMF1~3分量(a~c)和趋势项(d) Fig. 5 IMF compoents (a-c) and tendency change (d) of mean daily highest temperature during annual high temperature days in the Three Gorges area from 1961 to 2008 |
目前,数值模式尚不能有效解决长期气候预测问题,本文针对气候系统的非线性/非平稳性及现有预测方法的缺陷,尝试构建一个新的预测模型,其物理基础是气候层次理论,数学基础是非线性/非平稳序列的处理手段EMD方法。该预测模型首先利用EMD对气候序列进行平稳化处理,得到一组平稳分量IMF,该预测模型的样本序列主要由IMF分量组成;然后利用均生函数(MGF)模型分别对各IMF分量作均值生成函数延拓,选用几个相关较显著的IMF序列作为神经网络模型(BP)的输入层因子,相应的IMF(第一步分解结果)作为输出因子, 建立BP神经网络预测模型。选用BP神经网络的输入层节点为6,输出节点为1,隐节点为6,节点函数采用Sigmoid函数,学习因子取0.9,动量因子取0.7,设定网络模型的收敛误差为0.0001。最后用BP神经网络预测模型进行10年的预测,再将预测结果与对应的实况进行比较。
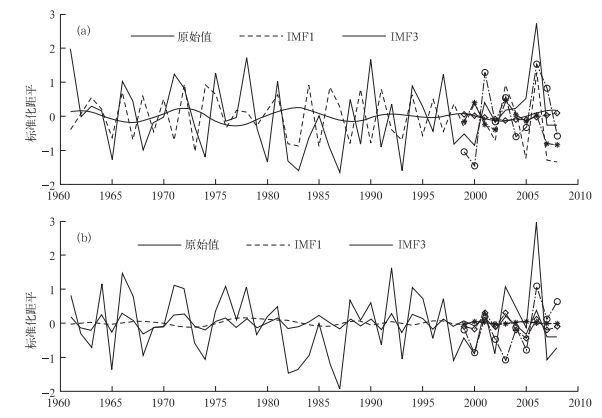
利用三峡库区高温序列的各IMF分量和1961—1998年的数据原始值,对其作均值生成函数延拓,采用BP神经网络模型对1999—2008年共10年进行预测,将实际数据作为测试样本,对预测结果进行评估。表 3给出了对三峡库区高温日数与高温日平均最高气温的预测效果,图 6只给出了方差贡献率大的两个IMF分量、原序列的预测值与实际值。根据表 3的预测评估效果,高温日数的IMF3分量拟合原序列的均方根误差RMSE为0.83,相关系数(R=0.46) 通过了0.001的显著性检验;IMF1拟合原序列的均方根误差RMSE为0.95,相关系数(R=0.39) 通过了0.01的显著性检验;同时还可以看出,原序列预测的均方根误差RMSE为0.92,相关系数为0.45,通过了0.01的显著性检验。IMF3、IMF1和原序列1999—2008年的预测与实况值(图 6a)比较可见,IMF3预测的效果较为理想。另外,IMF1与原始值的预测值基本比实况值偏小,但基本趋势与实况值相同。
|
|
表 3 对三峡库区高温日数与高温日平均最高气温的预测结果 Table 3 The forecast results of the high temperature days and mean daily highest temperature during annual high temperature days in the Three Gorges area |
|
图 6 三峡库高温日数(a)及高温日平均最高气温(b)的10步预测 Fig. 6 The curves of 10-step prediction (1999-2008) of the high temperature days (a) and mean daily highest temperature during annual high temperature days (b) in the Three Gorges area |
由均方根误差和相关系数可见(表 3),三峡库区高温日平均最高气温的IMF1均方根误差RMSE为0.83,相关系数(R=0.53) 通过了0.001的显著性检验;IMF2拟合原序列的均方根误差RMSE为0.84,相关系数(R=0.50) 通过了0.001的显著性检验;原序列预测的均方根误差RMSE为0.70,相关系数为0.59,通过了0.001的显著性检验。IMF1、IMF2和原序列的1999—2008年的预测与实况值(图 6b)比较可见,IMF1、IMF2预测的效果较为理想。原始值的预测值基本比实况值偏小,但基本趋势与实况值相同。
由表 2和3还可以看出,方差贡献率大的IMF分量,预测效果也较好。说明气候序列中方差贡献率大的IMF分量有重要的气候预测意义,它对原序列趋势的预测有重要指示意义。我们注意到,高温日平均最高气温EMD分解得到的IMF分量个数少于高温日数,而预测值与实际值的相关系数明显高于高温日数,这可能由于高温日数的变率较大,非线性/非平稳性更明显,多层次结构也更显著。
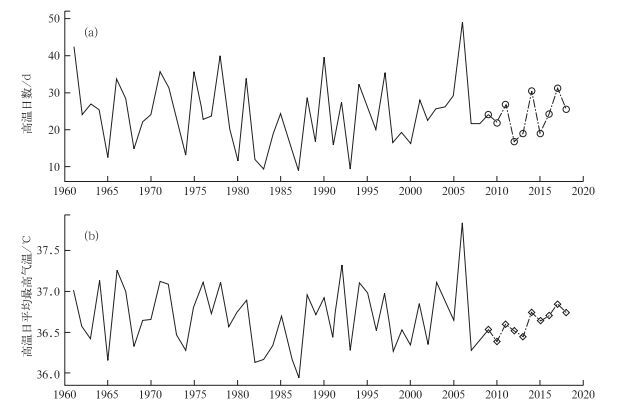
3.3 基于EMD的气候预测模型的三峡库区高温未来趋势预测利用1961—1998年三峡库区年平均高温日数和高温日平均最高气温的实况值,建立基于EMD的气候预测模型并对1999—2008年库区高温进行预测,预测值与实况值较为接近,预测的趋势变化与实际变化相同;这表明该模型具有一定的应用价值。根据1961—2008年的历史资料,采用所建立的基于EMD的气候预测模型,进一步计算2009—2018年三峡库区的年平均高温日数和高温日平均最高气温预测值;为了提高预测结果的稳定性,采用不同长度的时间序列(1961—2008年、1966—2008年、1971—2008年)作2009—2018年的预测,并将不同长度序列的预测结果进行加权平均作为2009—2018年的最终预测结果。如图 7所示,三峡库区未来10年高温日数有波动增多的趋势,年高温日数在16~32 d之间波动,2009—2013年高温日的平均最高气温变化幅度较小,2014—2018年有增强的趋势,高温日平均最高气温在36.3~37℃之间变化。
|
图 7 三峡库区高温日数(a)及高温日平均最高气温(b)的预测结果 Fig. 7 The forecast results of the high temperature days (a) and mean daily highest temperature during annual high temperature days (b) in the Three Gorges area |
(1) 三峡库区年均高温日数为24.07天,高温日平均最高气温为36.69℃。高温日数呈现山谷地区多,山区和丘陵少,库区北部多,东南部少的分布特征。高温日的平均最高气温库区东南部低,东北部较高。近48年来,三峡库区高温日数变化趋势存在明显的地域性差异,表现为东部与西部减少,中部增多的变化趋势。
(2) 除在20世纪80和90年代三峡库区高温日数和高温日平均最高气温为弱负距平外, 其他时期都为正距平。
(3) 三峡库区高温日数和高温日平均最高气温变化具有不同时间尺度的周期振荡,前者以3~5 a和16 a的周期变化为主,后者存在3 a左右和16 a的显著周期,同时具有较弱的上升趋势。
(4) 基于经验模态分解(EMD)方法建立的气候预测模型,不但能较好地拟合三峡库区高温日数和高温日平均最高气温的历史实况,而且对未来5~10年的演变趋势也具有一定的预报能力。预测结果表明,2009—2013年三峡库区高温日数和高温日平均最高气温波动幅度较小,与常年值较为接近,2014—2018年高温日数可能偏多,高温日的平均最高气温将有所上升。这种变化趋势形成的原因极其复杂,基于三峡库区气候历史演变特点,2009-2018年高温的变化,很可能是气候变化阶段性的反映,这有待进一步深入分析。
所建立的预测模型拓展了气候系统层次性理论的应用范围,研究取得了一些有积极意义的结果,但对预测值精度和对偶发极端气候事件的预测能力尚有待提高,如对2006年的高温事件,预测值比实际值明显偏小。还应指出的是,三峡水库的建成蓄水,水位抬升,水面扩大,对局地气候可能会有影响;目前虽有一些探索性研究[18-20],但由于针对三峡库区局地气候观测的资料长度有限,还不能充分揭示三峡水库对局地气候的影响及其程度,这需长期观测与研究。总之,EMD方法在气候年际预测业务中有良好的应用前景,如何更好地提高拟合精度及预报准确性尚值得进一步探讨。
| [1] |
万仕全, 封国林, 周国华, 等. 基于EMD方法的观测数据信息提取与预测研究[J]. 气象学报, 2005, 63(4): 516-525. DOI:10.11676/qxxb2005.051 |
| [2] |
李建平, 丑纪范. 气候系统全局分析理论及应用[J]. 科学通报, 2003, 48(7): 703-707. |
| [3] |
林振山. 气候层次理论及其应用[J]. 北京大学学报, 1990, 26: 355-360. |
| [4] |
Huang N E, Zheng S. The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis[J]. Proceedings of the Royal Society London, 1998, 454: 903-995. DOI:10.1098/rspa.1998.0193 |
| [5] |
孙卫国, 程炳岩. 河南省近50年来旱涝变化的多时间尺度分析[J]. 南京气象学院学报, 2000, 23(2): 101-105. |
| [6] |
程炳岩, 郭渠, 孙卫国. 川渝地区降水变化与Nino3区SST的关系及其稳定性分析[J]. 气象, 2010, 36(3): 27-33. DOI:10.7519/j.issn.1000-0526.2010.03.004 |
| [7] |
林振山, 汪曙光. 近四百年北半球气温变化的分析:EMD方法的应用[J]. 热带气象学报, 2004, 20(1): 90-96. |
| [8] |
刘莉红, 郑祖光, 琚建华. 基于EMD方法的我国年气温和东部年降水量序列的振荡模态分析[J]. 高原气象, 2008, 27(5): 1060-1065. |
| [9] |
刘莉红, 郑祖光, 琚建华, 等. 夏季副热带大气系统的多尺度振荡分析[J]. 高原气象, 2010, 29(1): 115-127. |
| [10] |
郑祖光, 李秀玲, 刘莉红, 等. 夏季副热带高压北移的非线性机理探讨[J]. 气象学报, 2005, 63(3): 278-288. DOI:10.11676/qxxb2005.028 |
| [11] |
魏凤英. 现代气候统计诊断与预测技术[M]. 北京: 气象出版社, 2007: 175-182.
|
| [12] |
陈永义. 支持向量机方法及其在气象中的应用[M]. 北京: 中国气象局培训中心, 2004: 6-9.
|
| [13] |
魏凤英, 黄嘉佑. 大气环流降尺度因子在中国东部夏季降水预测中的作用[J]. 大气科学, 2010, 34(1): 202-212. |
| [14] |
李永华, 高阳华, 廖良兵. 重庆地区年可利用降水资源的变化分析[J]. 南京气象学院学报, 2008, 31(3): 422-428. |
| [15] |
李永华, 刘德, 金龙, 等. BP神经网络模型在重庆伏旱预测中的应用研究[J]. 气象, 2003, 29(2): 14-18. |
| [16] |
张尚印, 宋艳玲, 张德宽, 等. 华北主要城市夏季高温气候特征及评估方法[J]. 地理学报, 2004, 59(3): 383-390. DOI:10.11821/xb200403008 |
| [17] |
叶殿秀, 邹旭恺, 张强, 等. 长江三峡库区高温天气的气候特征分析[J]. 热带气象学报, 2008, 24(2): 200-204. |
| [18] |
白莹莹, 高阳华, 张焱, 等. 气候变化对重庆高温和旱涝灾害的影响[J]. 气象, 2010, 36(9): 47-54. DOI:10.7519/j.issn.1000-0526.2010.09.008 |
| [19] |
张强, 万素琴, 毛以伟, 等. 三峡库区复杂地形下的气温变化特征[J]. 气候变化研究进展, 2005, 4(1): 164-167. |
| [20] |
林德生, 吴昌广, 周志翔, 等. 三峡库区近50年来的气温变化趋势[J]. 长江流域资源与环境, 2010, 19(9): 1037-1043. |
 2011, Vol. 37
2011, Vol. 37 