数值天气模式的定量降水预报(QPF)水平是预报员最关心的问题,也是数值模式发展过程中的重要环节,对数值模式降水预报进行各种评估是评价模式预报水平和提高预报员预报水平的重要手段[1-2]。传统的数值天气模式QPF的检验评估方法包括主观方法和客观方法[3]。主观方法是对数值模式预报的主要天气系统和观测进行主观分类、对比分析和统计,得出模式对某些天气系统的预报统计特征。由于主观方法评估模式需大量的人力资源,且天气系统的主观判别与人的主观因素有关,模式检验的主观方法将逐步被客观方法所取代。
QPF的客观检验方法可分为检验站点降水和检验格点降水两种[4],检验站点降水方法[5-11]是将数值模式格点场的要素预报场插值到台站地理位置上,与台站的观测要素进行“站点对站点”的对比分析和统计检验,该方法通常根据给定的一组降水阈值,由二分型列联表统计“预报-观测”一致与不一致的站点数,进而计算各种评分和指标。这种方法的优点是简单实用,可为预报员提供模式的基本特性和平均预报水平信息,我国国家气象中心[12-15]长期以来采用该方法。
随着模式分辨率的提高,精细化的中尺度数值天气预报模式与原有的大尺度天气模式相比提供了更细致、更丰富的预报信息,如果检验模式时仅考虑原有的少数站点的对比检验,有可能丢掉了精细化的中尺度数值天气预报模式的许多有用信息,因而这种检验方法对精细化的中尺度数值天气预报模式是不公平的,也不利于精细化模式的改进发展。因此,鉴于数值天气预报模式输出的格点特点和观测资料的不完整性,欧洲中期天气预报中心(ECMWF)、匈牙利气象局(ALADIN)等[16-21]业务预报中心都使用降水格点场资料对模式QPF进行客观检验。另外,我国国家气象中心即将发布全国格点分布的降水预报,更加需要掌握观测和模式输出的格点降水的特点。
鉴于我国目前较缺乏对比分析格点检验和站点检验降水预报效果的现状,本文先使用气象站和水文站组成的观测网得到的高密度降水资料,通过插值得到精细化的降水格点场,同时也将GRAPES模式的格点降水预报场插值到我国台站站点位置上,再采用经典评分方法,对模式降水进行“格点对格点”、“站点对站点”的检验,并对比分析了检验结果。此外,基于精细化的降水格点场,使用“面向目标”检验方法, 检验了GRAPES模式预报的5 mm以上降水事件的预报次数及空间分布特征。
1 降水资料与GRAPES模式简介 1.1 降水观测资料收集2006年6月1日至2008年5月31日全国所有县以上气象观测站08—08时(北京时)逐日的降水观测,同时收集水文部门与气象部门交换的所有水文站同期的降水资料。为了保证资料的一致性, 对两种资料进行对比分析和检验,去掉异常的值;如2007年10月18日水文站资料中山东东平(35.93°N, 116.58°E)出现了202 mm的降水,对比气象站降水及云图等资料,判断其为错误值。另外, 经整理发现,气象部门的日降水资料较完整,收集到的降水站点数目的每日变化不大,大体在2100到2300站之间。但能收集到的水文站日降水资料的数目变化很大,从0到2300多个。水文站日降水资料最多的时候是夏季,最少是冬季;主要分布在我国东部地区。
1.2 降水资料的插值与GRAPES模式简介 1.2.1 降水观测资料的网格化插值将上述收集到降水观测资料,在考虑降雨日数(降水频率)的情况下,通过使用Barnes插值和最近台站降水频率相结合的混合插值方案[22],将空间分布很不规则的台站逐日雨量数据转换成规则的0.15°网格数据,并使用交叉检验[23]的方法从方差分布、均方根误差、相关系数、绝对误差和偏差等方面分析、研究了这种插值方案的精度,结果表明:插值后的网格化降水资料与实际观测的降水分布和强度相当接近(表略), 能逼真地反映实测资料的各种特征。
1.2.2 模式降水资料的站点化插值同样使用Barnes插值方法,将与台站观测降水同时段的GRAPES模式2006年5月31日至2008年5月30日逐日08时输出的0~24 h降水预报场(0.15°格距)插值到与观测降水资料相同站点的地理位置上,形成GRAPES站点预报场,以便与观测降水进行站点到站点的检验。
1.3 GRAPES 3.0区域模式简介GRAPES模式是中国气象局新创建的业务数值天气预报模式[24]。该模式实现了静力与非静力可选、全球与有限区域可选、水平与垂直分辨率可选的通用框架,水平方向上采用经纬度的球面坐标,垂直方向采用高度地形追随坐标,并使用静力平衡的参考廓线,积分方案使用两时间层的半隐式、半拉格朗日时间差分方案,空间差分在水平方向上采用Arakawa C跳点格式,垂直方向上采用Charney-Philips跳点格式, 拉格朗日插值采用3维的准3次多项式,使用广义共扼余差方法求解关于气压扰动的3维Helmholtz方程。同化系统中同化了探空、云迹风和卫星辐射率等观测资料,其中卫星辐射率资料同化应用Rttov7模式,实现了红外、微波等辐射率资料同化的模块化。物理过程包括MRF边界层方案、Kain-Fritch积云对流参数化、CAMS微物理简冰方案、Dudhia短波辐射和RRTM长波辐射以及SLAB陆面过程模式。其区域模式的最新版本GRAPES Meso 3.0网格距为0.15°, 时间步长为30 s。
2 评分方法介绍 2.1 经典评分方法模式QPF检验通常根据给定的一组降水阈值,用二分型列联表(表 1)的统计结果来计算各统计量。
|
|
表 1 给定降水阈值下的预报与观测的二分型列联表 Table 1 Contingency table of forecast and observation events for a selected threshold |
通常,经典的检验统计量包括偏差(BIA)、公平T评分(ETS)和真实技巧评分(TSS)。计算公式分别是:
| $ BIA = \frac{{a + b}}{{a + c}} $ | (1) |
| $ ETS = \frac{{a-{a_r}}}{{a + b + c-{a_r}}} $ |
| $ 其中\;\;\;\;\;\;\;\;\;\;\;{a_r} = \frac{{\left( {a + b} \right)\left( {a + c} \right)}}{{a + b + c + d}} $ | (2) |
| $ TSS = \frac{a}{{a + c}}-\frac{b}{{b + d}} $ | (3) |
式(1) 中,BIA用来测量事件的频率而不考虑预报的准确率。当无空报、漏报(b=0,c=0) 时,其值等于1,预报完全准确;当漏报大于空报次数(c>b),其值小于1,预报不足;而当空报大于漏报次数b>c,其值大于1,预报过度。
式(2) 中,ETS是通过去掉随机预报的ar得到公平T评分,取值范围是-1/3~1。当无空报、漏报(b=0,c=0) 时,其值等于1,预报效果最佳;0及负数表示无预报技巧。
式(3) 中,TSS用来全面评价某级预报的总效果,即它不但包括降水事件的预报效果,还包括对非降水事件的预报效果。当降水和非降水事件的预报都准确(b=0,c=0),其值等于1,预报效果最好;当降水和非降水事件的预报都不准确(a=0,d=0),其值为-1,没有预报技巧。随机预报和固定预报的TSS评分是0;如果小概率事件预报准确,TSS评分也较高。
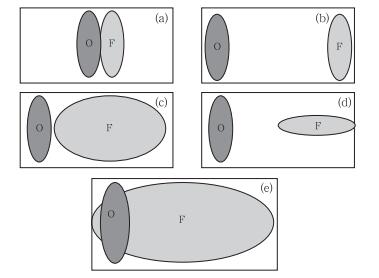
2.2 “面向目标”的检验方法上述经典统计量的统计结果不能给预报员和模式开发人员提供预报好坏的具体信息。例如:图 1给出的5个“预报-观测”例子中,(a)显然是很好的预报,只是位置有些偏移;(b)预报位置偏移太大;(c)预报区域太大;(d)不论预报的形状还是位置都与观测有较大差别,(e)实际是不好的预报,但却有正的预报技巧。因此,这种点对点检验不能很好地区分预报和观测位置和形状的差别。
|
图 1 各种预报和观测组合示意图 Fig. 1 A schematic example of various forecast and observation combinations |
与传统的点对点评分不同,“面向目标”的检验方法可直接检验模式区域内天气事件主要特征的预报能力[25-28],该方法既能模仿预报员决定模式降水预报好坏的一些特性,例如对比预报降水的区域面积、强度等指标;也能客观地识别观测和预报目标(即降水事件中的雨团),对比这些目标的几何图形参数,例如预报和观测目标的位置、形状、方向和大小等的特征。
3 检验结果 3.1 “格点对格点”的检验结果分析根据公式(1)~(3),以1.2.1节中格点化的降水观测资料为基础,对GRAPES模式2006年5月31日至2008年5月30日逐日08时输出的0~24小时降水预报(0.15°格距)进行分量级的检验。
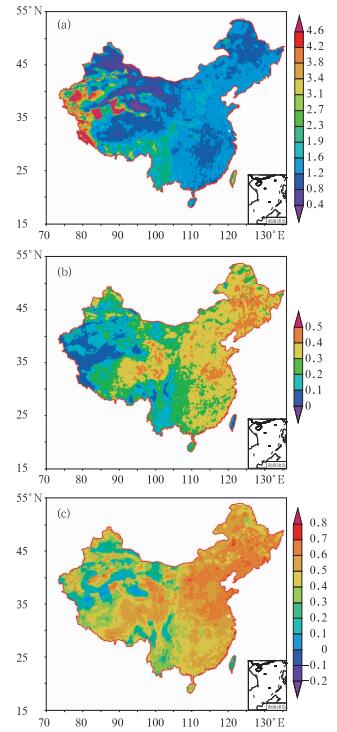
GRAPES模式小雨(0.1~9.9 mm)预报格点评分结果见图 2。从图 2可见,GRAPES模式小雨预报的BIA值(0.8~1.2) 在我国东部(105°E以东)和青藏高原中东部接近观测(图 2a),表明模式对这些地区的小雨预报基本正确,空、漏报较少;但在青藏高原西部等地形的迎风坡明显偏强(>3.8),显示出模式对该地区的空报过多;而在青藏高原北部和天山北部地区偏弱( < 0.8),说明模式对该地区的漏报多。从ETS(图 2b)来看,相对而言, 我国东部和青藏高原东北部的预报效果较好(>0.3),特别是青藏高原东北部、江淮和东北地区预报效果最好(>0.4);而在青藏高原西部等地几乎没有预报技巧( < 0.1)。从TSS(图 2c)来看,预报效果较好(>0.6) 的地区与图 2a中BIA值在0.8~1.6的区域分布一致,即我国东部和青藏高原东北部,特别是甘肃中南部和青海东北部、东北平原、华北平原和江淮预报效果最好(>0.7);另外在青藏高原北部沿昆仑山的部分地区和沿天山一带预报效果也较好;表明模式对这些地区的小雨预报和无小雨事件的预报都比较好。而青藏高原西部和西南地区东部预报效果较差( < 0.3)。
|
图 2 “格点对格点”小雨的检验结果 (a) BIA;(b) ETS;(c) TSS Fig. 2 Gridbox validation of light rain (a) BIA, (b) ETS, (c) TSS |
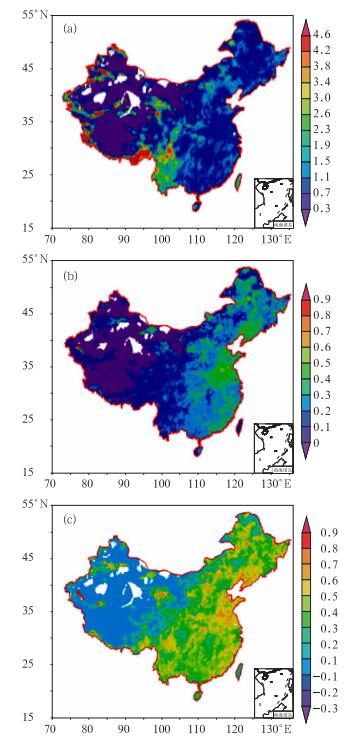
GRAPES模式中雨(10.0~24.9 mm)预报格点评分结果见图 3。从图 3可见,GRAPES模式中雨的预报效果总体上与小雨基本类似。即BIA值(图 3a)在我国东部的大部分地区为1.0左右,预报接近观测,比较成功;但在阿尔泰山、天山地区、青藏高原东北部、西部和南部的边缘地区、西南地区等地形的迎风坡偏强(>3.8),表明模式对该地区中雨的空报过多;而在其他地区 < 0.3,存在明显的漏报现象。从ETS(图 3b)来看, 我国105°E以东地区、天山东部、内蒙古西部的预报效果略好(>0.3),其中东北南部、华北平原南部、黄淮和江淮等地区预报效果较好(>0.4);而在我国105°E以西地区预报效果普遍较差( < 0.1),基本无预报技巧。从TSS来看(图 3c),模式对天山地区和我国100°E以东的部分地区的预报效果较好(>0.5),特别是东北南部、华北平原西部、黄淮和江淮等地区预报效果最好(>0.7),显示该地区中雨和无中雨的预报基本准确;而在我国100°E以西的预报效果较差( < 0.1),几乎无预报技巧。另外,ETS和TSS都显示在塔里木盆地的西南角有>0.8的值,虽然该地中雨比较少,但模式还是有较高的预报技巧。
|
图 3 “格点对格点”中雨的检验结果 (a) BIA;(b) ETS;(c) TSS Fig. 3 Gridbox validation of moderate rain (a) BIA, (b) ETS, (c) TSS |
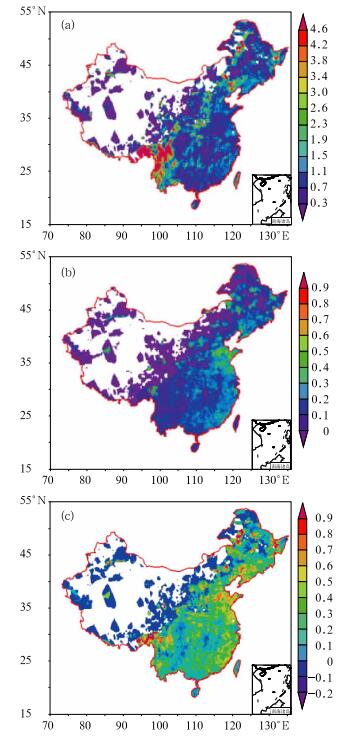
GRAPES模式大雨(25.0~49.9 mm)预报格点评分结果见图 4。图中显示GRAPES模式对的大雨预报的BIA值在我国东部的部分地区为1.0左右,其中东北、华北和东部沿海的局部地区预报效果较好,而西南地区明显偏强(>3.8), 表明大雨空报太多(图 4a); 我国西部BIA值 < 0.3, 这与该地区大雨量级的降水较少, 且漏报较多有关。从ETS来看(图 4b),模式对我国东部的部分地区有一些预报技巧(>0.3), 其中东北和华北的局部地区、黄淮、江淮和横断山脉西部等的部分地区预报效果较好(>0.4);而其他地区基本无预报技巧。从TSS来看(图 4c),东北南部、华北、黄淮、江淮和横断山脉西部等的部分地区预报效果较好(>0.5), 东南沿海和天山沿线的局部地区次之(>0.4), 说明模式对这些地区的大雨和无大雨事件的预报比较成功;而其他地区基本无预报技巧。
|
图 4 “格点对格点”大雨的检验结果 (a) BIA;(b) ETS;(c) TSS Fig. 4 Gridbox validation of heavy rain (a) BIA, (b) ETS, (c) TSS |
GRAPES模式暴雨(≥50.0 mm)预报格点评分结果表明(图略):模式暴雨预报的BIA值在我国东部和南部沿海的部分地区接近1.0, 效果较好, 这与主要暴雨分布在我国东部和南部有关; 而其他地区基本上都 < 0.3。ETS和TSS值>0.5的地区主要零星地分布在辽宁东部、山东、江苏、湖北北部、西藏东南部和华南等的局部地区,其他地区基本无预报技巧。
总之,尽管各级别降水的检验结果在某些地域有所差异,但从总体上看来GRAPES模式小雨、中雨的预报效果明显好于大量级的降水。模式在我国东部的预报效果好于西部,平原地区好于山区,这与我国降水主要分布在东部有关; 青藏高原、天山等地形迎风坡会使得预报的降水偏强, 空报过多, 而青藏高原上空和新疆北部则以漏报为主。
3.2 “站点对站点”的检验结果分析以1.2.2节中的为插值后的GRAPES模式站点降水预报为基础,利用同时段的站点降水观测资料,同样根据公式(1)~(3),进行分量级的评定。
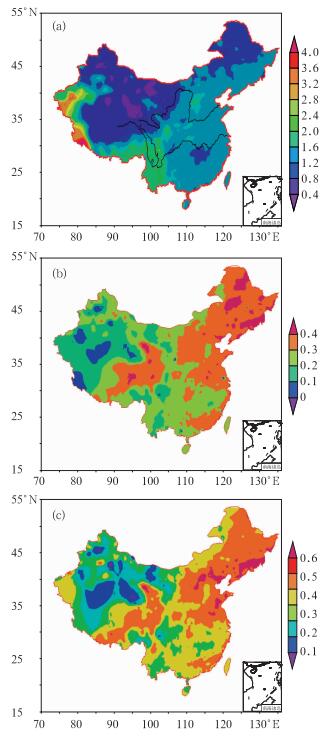
GRAPES模式小雨(0.1~9.9 mm)预报站点评分结果见图 5。与图 2相比, GRAPES模式对小雨站点检验的结果与格点基本一致,但ETS和TSS最大值分别为0.4和10.6,低于格点检验的0.5和0.8,表明格点检验的预报技巧整体上高于站点。具体而言,BIA值在我国东部(105°E以东)和青藏高原东部为0.8~1.2,模式预报接近观测(图 5a); 在青藏高原西部等地形的迎风坡明显偏强(>3.2),但空报的范围不及格点检验的多;而在青藏高原中部和北部、内蒙古西部和天山以北等地区偏弱( < 0.8),但漏报的范围比格点检验的多。从ETS(图 5b)来看,西北地区东部、西藏东部和东北的局部地区预报效果最好(>0.4),其范围比对应值格点检验的小;而在青藏高原中部和南部等的部分地区几乎没有预报技巧( < 0.1)。从TSS(图 5c)来看,甘肃中南部、东北东部、华北平原和江淮东部预报效果较好(>0.6),但其范围也比对应值的格点检验的小;而青藏高原中部预报效果较差( < 0.1)。
|
图 5 “站点对站点”小雨的检验结果 (a) BIA;(b) ETS;(c) TSS Fig. 5 Station validation of light rain (a) BIA, (b) ETS, (c) TSS |
GRAPES模式中雨(10.0~24.9 mm)预报站点评分结果(图略)表明,BIA值在我国东部的大部分地区为1~2,空报略多;但在青藏高原西部和南部边缘地区达10~12,表明模式对该地区的空报太多;从ETS来看, 我国110°E以东地区、天山东部、内蒙古西部的预报效果较好(>0.3),此范围比对应ETS值的格点检验的要小一些,其中东北、黄淮和江淮等地区预报效果最好(>0.4)。从TSS来看,模式对天山东部和100°E以东的部分地区的中雨和无中雨的预报基本准确(>0.5),这与格点检验的范围一致,但TSS>0.7的区域仅零星地东北地区,范围比对应值的格点检验的小的多。另外,站点检验的结果也显示我国100°E以西的预报效果较差( < 0.1),几乎无预报技巧。
GRAPES模式大雨(25.0~49.9 mm)预报站点评分结果(图略)显示BIA值在青藏高原南部达12以上,表明模式对大雨空报异常偏多, 而我国东部的部分地区为1~3。从ETS来看,模式对我国东部的部分地区的大雨有一些预报技巧(>0.3), 其中东北和华北的局部地区以及横断山脉西部等的部分地区预报效果较好(>0.5), 但这些范围比对应ETS值的格点检验的小;而其他地区基本无预报技巧。TSS值>0.4的范围比格点检验的小一些;另外,模式对大雨和无大雨事件的预报最成功的地区主要分布在东北南部和横断山脉西部等,也比格点检验的范围小。
GRAPES模式暴雨(≥50.0 mm)预报站点评分结果(图略)显示模式对暴雨基本没有预报技巧。这与暴雨出现次数少及模式空、漏报有关。
综上所述,站点检验和格点检验的结果总体趋势是一致的,特别是对于小雨量级的降水,两种方法检验的结果的相差不大,但对于大量级(中雨及以上)的降水,站点检验的偏差值异常大,显示出模式对大量级的降水预报过度。格点检验的ETS和TSS值比站点检验的高,预报效果较好的区域范围也比站点检验的大,表明格点检验比站点检验能更好地反映GRAPES模式的预报能力。
3.3 “面向目标”检验方法对GRAPES模式的检验结果根据1.2.1节中2006年6月1日至2008年5月31日格点化的逐日降水资料(站点资料不规则,不能使用该方法),抽象出降水的强度分布和区域大小等信息,利用“面向目标”的方法,对同时段(2006年5月31日至2008年5月30日)GRAPES模式0~24小时0.15°格点降水预报的总体空间分布特征进行检验评估。具体做法是:通过多次水平面上正平滑和逆平滑处理,分别过滤出观测和预报中5 mm以上的降水雨团。雨团直径是拓扑结构为相邻降水大于某一阈值(5 mm)的格点组成的雨团面积的平方根。
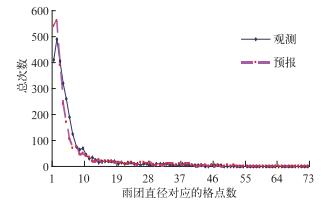
图 6给出了5 mm以上降水预报(虚线)和观测(实线)的年平均总次数与雨团直径大小的分布关系图。图中可以看出GRAPES模式预报5 mm以上降水的总次数与雨团直径大小的变化趋势同观测非常一致;在格点数为3即雨团直径为45 km时, GRAPES模式预报和观测的总次数达到最多, 但预报次数略多与观测次数;特别是在格点数为4即雨团直径为60 km时, GRAPES模式预报的次数与观测相等, 表明模式对该直径雨团的预报效果最好;而在格点数为10即雨团直径为150 km时, GRAPES模式预报和观测的总次数同时迅速减少。也表明我国5 mm以上降水雨团的空间尺度主要为β中尺度。
|
图 6 5 mm以上降水预报(虚线)和观测(实线)的年平均总次数与雨团直径大小分布关系图 Fig. 6 The distribution of annual precipitation number against the cluster size of forecast (dashed) and observation (solid) for the threshold more than 5 mm |
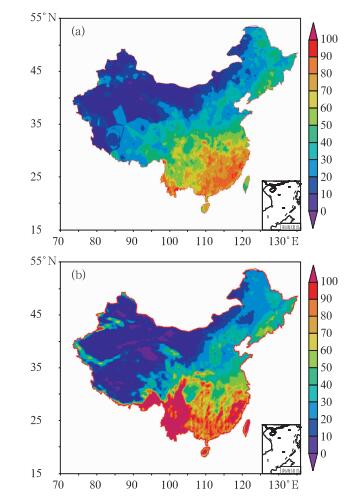
图 7反映了5 mm以上降水次数年平均的地域分布特点,GRAPES模式预报5 mm以上降水的次数在内蒙古东部、东北、华北、江淮、陕西、甘肃南部、青藏高原东部等地与观测次数相当;这与我国西高东低的地形分布特点基本一致;而在长江以南预报多于观测次数,尤其是在西南地区东部明显偏多;另外沿天山和昆仑山一带也是预报次数偏多的地区,但在我国西部高原的大部分地区预报次数却少于观测次数。这些与3.1和3.2中用经典评分方法分析的结果一致,也表明地形对降水的分布和模式降水预报都有一定的影响。
|
图 7 5 mm以上降水年平均的次数分布图 (a)观测; (b)预报 Fig. 7 Spatial distributions of annual precipitation number for the threshold more than 5 mm (a) Observation, (b) Forecast |
经上述对比分析表明,两种点对点的检验结果都显示GRAPES模式在我国东部平原地区预报效果较好; 在地形复杂的西部山区的降水预报能力偏弱。而对于各量级的降水,总体上格点检验结果好于站点检验,特别是中雨及以上的降水,站点检验的偏差值异常大,模式的空报率太高,而格点检验的偏差值则要小得多;格点检验的ETS和TSS的值比站点检验的高,预报效果较好的区域范围也比站点检验的大。
使用插值后的精细化格点降水资料来检验数值模式降水预报比站点检验能更清楚地得到模式的评分结果,模式开发人员和预报员可以更加直观、具体、准确地掌握全国各地的降水评分分布及其特点,为模式降水的检验提供了一种新途径。更进一步地,根据精细化格点降水资料,采用“面向目标”的客观检验方法,分析研究了模式对区域内天气事件主要特征的预报能力,特别是GRAPES模式对空间尺度为60 km左右的雨团有较好的预报能力。
使用站点观测降水进行QPF检验的方法存在两方面的不足,一方面是将模式要素格点场分析插值到台站上的方法有多种,各种方法之间存在差别,分析插值方法不同将引起检验误差;由于观测站点的分布很不均匀,站点稀疏地区广大但参与评估的站点稀少,统计的平均预报水平可能导致检验统计中对站点稀疏地区的预报水平高估,从而掩盖模式发展中的问题。另一方面,数值天气模式的降水预报包括大尺度凝结和次网格对流,理论上它应该是该网格的平均降水,但观测站降水是点降水。将观测站的点降水插值到模式格点上再进行统计检验能克服站点检验的缺陷,比将模式降水预报插值到站点进行统计检验应能更准确地反映模式的特点。
另外,随着“升尺度”[19, 29]格点化技术不断改进,能得到越来越逼真的降水精细格点化资料,可充分利用这些格点化的降水资料来检验中尺度数值天气预报模式的降水预报,为模式降水评估提供另一种的选择。
| [1] |
Murphy A H, Winkler R L. A general framework for forecast verification[J]. Mon Wea Rev, 1987, 115: 1330-1338. DOI:10.1175/1520-0493(1987)115<1330:AGFFFV>2.0.CO;2 |
| [2] |
Casati B, Wilson L J, Stephenson D B, et al. Forecast verification: current status and future directions[J]. Meteorol Appl, 2008, 15: 3-18. DOI:10.1002/(ISSN)1469-8080 |
| [3] |
Kain J S, Baldwin M E, Janish P R, et al. Subjective verification of numerical models as a component of a broader interaction between research and operations[J]. Wea Forecasting, 2003, 18: 847-860. DOI:10.1175/1520-0434(2003)018<0847:SVONMA>2.0.CO;2 |
| [4] |
Yates E, Anquetin S, Ducrocq V, et al. Point and areal validation of forecast precipitation fields[J]. Meteorol Appl, 2006, 13: 1-20. |
| [5] |
Christopher A, Stefano M, Marco C, et al. Verification of precipitation forecasts from two limited-Area models over Italy and comparison with ECMWF forecasts using a resampling technique[J]. Wea Forecasting, 2005, 20: 176-200. |
| [6] |
Tiziana C, Ghelli A, Lalaurette F. Verification of precipitation forecasts over the Alpine region using a high-density observing network[J]. Wea Forecasting, 2002, 17: 238-249. DOI:10.1175/1520-0434(2002)017<0238:VOPFOT>2.0.CO;2 |
| [7] |
Christopher A, Mariani S, Casaioli M. Sensitivity of precipitation forecast skill scores to bilinear interpolation and a simple nearest-neighbor average method on high-resolution verification grids[J]. Wea Forecasting, 2003, 18: 918-932. DOI:10.1175/1520-0434(2003)018<0918:SOPFSS>2.0.CO;2 |
| [8] |
Harris D, Foufoula-Georgiou E, Droegemeier K K, et al. Multiscale statistical properties of a high-resolution precipitation forecast[J]. J Hydromet, 2001, 2: 406-418. DOI:10.1175/1525-7541(2001)002<0406:MSPOAH>2.0.CO;2 |
| [9] |
管成功, 王克敏, 陈晓红. 2002—2005年T213数值降水预报产品分析检验[J]. 气象, 2006, 32(8): 70-76. DOI:10.7519/j.issn.1000-0526.2006.08.012 |
| [10] |
周慧, 崔应杰, 胡江凯, 等. T639模式对2008年长江流域重大灾害性降水天气过程预报性能的检验分析[J]. 气象, 2010, 36(9): 60-67. DOI:10.7519/j.issn.1000-0526.2010.09.010 |
| [11] |
尤凤春, 魏东, 王雨. 北京奥运期间多模式降水检验及集成试验[J]. 气象, 2009, 35(11): 3-8. DOI:10.7519/j.issn.1000-0526.2009.11.001 |
| [12] |
王雨, 闫之辉. 降水检验方案变化对降水检验评估效果的影响分析[J]. 气象, 2007, 33(12): 61. |
| [13] |
李勇, 王雨. 2007年夏季GRAPES_Meso 15及30 km模式对比检验[J]. 气象, 2008, 34(10): 81-89. DOI:10.7519/j.issn.1000-0526.2008.10.011 |
| [14] |
王雨. 2004年主汛期各数值预报模式定量降水预报评估[J]. 应用气象学报, 2006, 17(3): 316-324. |
| [15] |
闫之辉, 王雨, 朱国富. 国家气象中心业务数值预报发展的回顾与展望[J]. 气象, 2010, 36(7): 26-32. DOI:10.7519/j.issn.1000-0526.2010.07.007 |
| [16] |
Tustison B, Harris D, and Foufoula-Georgiou E. Scale issues in verification of precipitation forecasts[J]. J Geophys Res, 2001, 106 (D11), 11:775-784.
|
| [17] |
Weygandt S S, Seaman N L. Quantification of predictive skill for mesoscale and synoptic-scale meteorological features as a function of horizontal grid resolution[J]. Mon Wea Rev, 1994, 122: 57-71. DOI:10.1175/1520-0493(1994)122<0057:QOPSFM>2.0.CO;2 |
| [18] |
Gabriella C, Anna G. On the use of the intensity-scale verification technique to assess operational precipitation forecasts[J]. Meteorol Appl, 2008, 15: 145-154. DOI:10.1002/(ISSN)1469-8080 |
| [19] |
Gheli A, Lalaurette F. Verifying precipitation forecasts using upscaled observations[J]. ECMWF Newsletter, 2000, 87: 9-17. |
| [20] |
Rodwell M J, Richardson D S, Hewson T D. A new equitable score suitable for verifying precipitation in NWP[M]. ECMWF Tech Memo, 2010: 37.
|
| [21] |
Keil C, Craig G C. A displacement and amplitude score employing an optical flow technique[J]. Wea Forecasting, 2009, 24: 1297-1308. DOI:10.1175/2009WAF2222247.1 |
| [22] |
胡江林, 张人禾, 牛涛. 长江流域0.1°网格逐日降水数据集及其精度[J]. 自然资源学报, 2008, 23(1): 136-149. DOI:10.11849/zrzyxb.2008.01.016 |
| [23] |
Elsner J B, Schmertmann C P. Assessing forecast skill through cross validation[J]. Wea Forecasting, 1994, 9: 619-624. DOI:10.1175/1520-0434(1994)009<0619:AFSTCV>2.0.CO;2 |
| [24] |
张人禾, 沈学顺. 中国国家级新一代业务数值预报系统GRAPES的发展[J]. 科学通报, 2008, 20: 2393-2396. DOI:10.3321/j.issn:0023-074X.2008.20.001 |
| [25] |
Ebert E E, McBride J L. Verification of precipitation in weather systems: Determination of systematic errors[J]. J Hydrology, 2000, 239: 179-202. DOI:10.1016/S0022-1694(00)00343-7 |
| [26] |
Davis C, Brown B, Bullock R. Object-based verification of precipitation forecasts. Part Ⅰ: Methods and application to mesoscale rain areas[J]. Mon Wea Rev, 2006, 134: 1772-1784. DOI:10.1175/MWR3145.1 |
| [27] |
Marzban C, Sandgathe S. Cluster analysis for verification of precipitation fields[J]. Wea Forecasting, 2006, 21: 824-838. DOI:10.1175/WAF948.1 |
| [28] |
Daly C, Neilson R P, Phillips D L. A statistical-topographic model for mapping climatological precipitation over mountain terrain[J]. Journal of App Meteorology, 1994, 33: 140-158. DOI:10.1175/1520-0450(1994)033<0140:ASTMFM>2.0.CO;2 |
| [29] |
高学杰, 徐影, 赵宗慈, 等. 数值模式不同分辨率和地形对东亚降水模拟影响的试验[J]. 大气科学, 2006, 30(12): 185-192. |
 2011, Vol. 37
2011, Vol. 37 