2. 北京市气象局, 北京 100089;
3. 河北农业大学理学院数学系, 保定 071001
2. Beijing Meteorological Bureau, Beijing 100089;
3. Department of Maths, College of Science, Agricultural University of Hebei, Baoding 071001
多普勒天气雷达可以获得降水强度和相应范围内风场径向分量的信息,且时空分辨率远高于常规探空资料[1-2]。近年来,我国新一代多普勒天气雷达网的建设也逐步完成,且雷达资料的反演和同化研究取得了很大进展[3],相应地,多普勒雷达资料已被广泛应用于强对流天气的探测分析、诊断研究以及短时和临近预报等领域[4-9]。因此,多普勒雷达径向速度模糊问题和退模糊技术也相应地受到了更多的重视[10]。
多普勒天气雷达基于多普勒效应获得目标物相对于雷达的径向移动速度,其所能测到的最大径向速度称为最大不模糊速度或Nyquist速度,它与采样频率(雷达脉冲重复频率)PRF和波长有关。当目标物相对于雷达的运动速度超过最大不模糊速度时就会发生折叠现象,也称作速度模糊现象。雷达可以正确测量的速度值范围是±Vmax,观测到的径向速度值和真实的径向速度满足如下关系:
| $ {V_T} = {V_0} \pm 2n \times {V_{\max }} $ | (1) |
其中,VT为真实的径向速度值,V0为径向速度观测值,n为整数,称为Nyquist数。
目前,速度退模糊既可以通过硬件也可以通过软件的方法来实现,但硬件退模糊技术实施起来比较困难。所以近年来,专业人员相继提出了很多软件退模糊方法。最简单的方法即Ray等[11]提出的单径向上“点-点”对比法。20世纪80年代初Bargen和Brown[12]改进了这种单径向法,沿着每根径向利用空间连续性去除单点模糊。1984年Merritt[13]提出了一个较为有力的二维方法,后被Boren,Bergen等[14-15]进一步发展完善。1990年Elits等[16]使用“双径向”方法进行速度退模糊,对正确率和计算时间都有所改善。2001年, James等[17]将退速度模糊的思想扩展到四维(包括时间)。此外,为了解决非多普勒雷达探测资料构造的参考场遇到的空间和时间不匹配的问题,Tabary等[18]提出的Modified VAD方法,Gao等[19]提出的GVAD方法及Gunther等[20]提出的圆环面方法,都是在包含模糊现象的径向风速资料中通过径向速度的方位梯度信息估计各个高度上的水平风速。与国外相比,国内在这一方面的研究成果还不多。比较有代表性的是梁海河等[21]提出的对多普勒天气雷达的风场信息进行预处理的“K-邻域频数法”。
然而,软件方法主要基于连续性原则,当实际风场存在强切变,相邻库上的实际径向风相差很大时,连续性原理不再适用,而且当最大不模糊速度较小或风场信息中噪声较大时,退模糊难度也会相应增加。所以,不可避免地,各种退速度模糊的方法都或多或少地存在一些弊端。
本文介绍从美国强风暴实验室(NSSL)引进了一种最新的退速度模糊的算法,叫做二维多途径退速度模糊算法[22]。目前,这个新算法在美国主要是用于科研,并没有推广到业务上运行。我们引进新算法之后,认为它能从雷达速度观测值中得到更精确、可靠的参考速度,能消除对于外在风场数据的依赖性,且有更高的实时计算效率,所以考虑把这个新算法应用到国内雷达资料中,并结合国内雷达资料的情况,开展相关的工作,并有意到国内业务上试运行。
本文的第一部分介绍了新算法以及使用新算法前的一些数据预处理工作;第二部分把新算法应用到我国新一代天气雷达(SA、CB)观测的台风和强对流风暴天气过程的资料质量控制中,进行了退模糊试验,详细说明了新算法的特点,且分析了地物回波对退速度模糊效果可能的影响;第三部分进行了讨论与总结。
1 二维多途径退速度模糊算法二维多途径退速度模糊算法的主要思想是,首先通过找到最弱的风场区来决定一系列初始参考径向和距离库,然后从这些径向和距离库出发,检查相邻库的连续性并对模糊速度进行订正。
该算法主要基于风场连续性原则,相对于其他软件退速度模糊算法而言,主要有三方面的特点。一方面是利用三根径向同时作为参考径向来进行速度退模糊处理,这可以避免退模糊过程中存在太多的错误扩散;二是在退模糊过程中,从顺时针和逆时针两个方向同时逐根径向进行处理,这能更好地处理切变区域周围的径向速度模糊,同时也限制了180°范围内任何可能的错误扩散。并且处理时,首先退方位角方向,再退径向方向。仅仅从方位角方向进行处理,在回波边缘区域容易出现错误,因为回波边缘区域相邻径向之间的距离相隔较大,容易存在风切变。而径向方向上的退模糊处理可能会修改之前方位角方向上不正确的处理结果;三是在退速度模糊处理过程中,共进行两轮处理。其中,第一轮退速度模糊确定参考速度的标准是很严格的,因此在这轮被处理过的速度值可以认为是具有高准确性的。在第二轮退速度模糊处理中,会对这一轮没能正确进行处理的距离库进行处理,经过第一轮处理之后,会存在更多好的距离库,则更利于找到有效的参考速度。
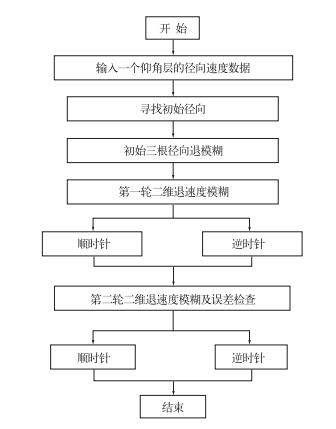
该算法简单独立能自动化运行,计算性能较高,主要包括四个步骤(图 1)。
|
图 1 自动化二维多途径退速度模糊方法总体流程图 Fig. 1 An overview flowchart of the automated 2-D multi-pass velocity dealiasing algorithm |
以前的退速度模糊方法往往是通过诸如上层风探测或者VAD技术等获得的背景风场资料确定初始参考径向,但背景风场有时候由于观测条件上时间和空间的限制并不能准确地描述速度情况。在初始参考径向的选取上,新算法利用的是雷达观测本身得到的径向速度值。在某一给定仰角上,通过计算每根径向的有效库数来选取一系列好的径向或者是相对而言速度不模糊的径向。
所谓好的径向,即任意相邻距离库之间都没有大的风切变:
| $ \left| {{V_i}-{V_{i-1}}} \right| < \alpha {V_{\max }} $ | (1) |
式中V是径向速度;i=1,2,…,N,表示所有有效的速度距离库;α是一个参数,缺省值为0.75。
对于好的径向,把满足条件的径向速度值平均:
| $ {V_{M1}} = \frac{1}{{{N_1}}}\sum\limits_i {{V_i}} \;\;\;\;\;\;\;\;\left| {{V_i}} \right| < \beta {V_{\max }} $ | (2) |
式中N1是径向速度值在±βVN之间的速度距离库库数,也即有效距离库库数,β是一个参数,缺省值为0.4。
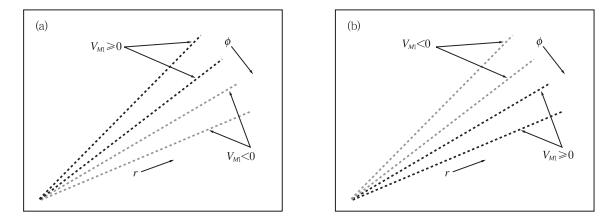
相邻的四根径向当中,如果前两根径向的VM1和后两根径向的VM1正负符号相反,则认为中间两根径向中,有效库数较多的那一根即为初始径向(图 2)。
|
图 2 寻找初始径向的方法,r指径向方向,ϕ指方位角方向。(a)、(b)两张图说明了相邻四根径向中,前两根径向的VM1和后两根径向的VM1两种可能出现的不同情况,而中间两根径向中,有效库数较多的那一根被认为是初始径向[18] Fig. 2 An illustration of the initial approach for searching the Initial Radial. Here "r" indicates radial direction and "ϕ" indicates azimuth direction. The two pictures illustrate two possible scenarios where VM1 changes sign from two consecutive radials to the next consecutive radials. The initial radial is chosen as one of the two middle radials with a larger N1 |
否则,需要重新进行第二轮选择:某根径向任意相邻距离库之间没有大的风切变,并且有效距离库较多(N。缺省为40),且所有有效速度的平均值:
| $ {V_{M0}} = \frac{1}{{{N_0}}}\sum\limits_i {{V_i}} $ | (3) |
需满足条件:
| $ {V_{M0}} < \beta {V_{\max }} $ | (4) |
则被认为是好的径向,在所有满足条件的径向当中,选择VM0最小的径向为初始径向。如果所有径向均不满足条件,则可以降低有效距离库的标准,直到找到初始径向为止。但有效距离库不得低于5,并且一定要满足VM0 < βVN,否则认为这层仰角上没有合适的初始径向,也就不进行退模糊处理。
1.2 对初始的三根径向进行退模糊找到初始径向之后,首先利用VM1或VM0作为参考速度对这根径向上的所有点进行退模糊,然后利用这根径向,对相邻的两根径向进行径向速度退模糊处理,这样可以得到三根好的初始径向。
1.3 第一轮逐根径向退模糊不同于其他算法,该算法用得到的三根好径向同时作为参考径向来进行第一轮退模糊。算法从紧挨着三根初始径向的那根径向出发,从顺时针和逆时针两个方向同时逐根径向进行退模糊。处理过程中,先进行方位角方向的处理,再进行径向方向的处理。
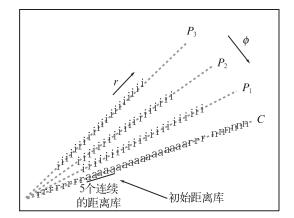
沿着方位角方向,每根径向上的速度库是以相邻三根径向同一距离上三个速度库的平均值VR为参考速度来做处理的,这样可以避免因为参考库的错误而导致退模糊失败(图 3)。
|
图 3 第一轮逐根径向退模糊 P1、P2、P3是三根参考径向,i是经过退模糊处理的正确点;C是需要处理的径向,a表示经过方位角方向退模糊处理后得到的点,r表示经过径向方向退模糊处理后得到的点;n指的是在这一轮中没有被处理的点[18] Fig. 3 Radial-by-radial dealiasing using the first three reference radials The "i" points indicate the already dealiased velocity gates in three preceding radials(P1, P2, and P3) The "a" points indicate velocities in the current radial(marked as "C") that are dealiased using the average of the three preceding gates in azimuth direction; the "r" points indicate velocities that are dealiased along radial direction using the "a" gates; and the "n" gates indicate unprocessed gates |
这三个库的选择需满足以下条件:均是经过处理且正确的距离库;任意相邻的两个库必须满足公式(2);并且V和VR之间需满足|V-VR| < αVN(V为需要处理的库)。如果没有满足上述三个条件的VR,则该库在方位角方向不被处理。
方位角方向处理结束之后,开始径向方向的处理,首先通过沿径向朝雷达方向搜索来选择初始库,然后从初始库开始,沿着朝向雷达以及远离雷达的两个方向同时进行退速度模糊处理。
初始库同样需要满足三个条件:远离回波边缘;其必须是经过处理且具有高准确性的点,径向方向上在其两边至少各有两个正确的距离库,这五个库需要满足公式(2);在方位角方向上,至少有三个相邻的正确的距离库,且这三个库同样需要满足公式(2)。
如果在搜索初始库或者进行退模糊处理时,遇到无效数据或者是距离折叠区域,那就越过重新寻找新的初始库,直到径向边缘。
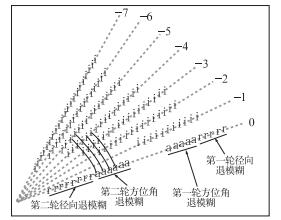
1.4 第二轮逐根径向退模糊在这个步骤中,会对第一轮退速度模糊当中没处理的距离库进行处理,在寻找参考速度时,算法在方位角方向扩大了搜索半径,除此以外,其他方法和第一轮相同(图 4)。
|
图 4 第二轮径向逐根退模糊 “0”是需要处理的径向,“-1”到“-7”是已经经过处理的径向,i是好的距离库或者是经过退速度模糊处理的距离库。“0”径向上灰色的a和r是在第一轮中被处理过的距离库。黑色的a和r分别是在第二轮中通过方位角方向和径向方向被处理的距离库[18] Fig. 4 An illustration of the 2rd round radial-by-radial dealiasing procedure Radial "0" represents the current radial under processing. Radials "-1" to "-7" represent the preceding radials that have been processed and "i" points indicate "good"(dealiased) velocity gates. The grey "a" and "r" points are "good" velocities that have been dealiased in the 1st round radial-by-radial dealiasing. The black "a" and "r" points represent the velocity gates that are dealiased in the 2rd round radial-by-radial dealiasing |
本文首先调通算法,并将其应用到国内雷达资料上。在对雷达资料处理的过程中发现,雷达在进行体积扫描时,某一仰角层扫描起始位置和终止位置往往并不一致(图 5),也即第一根径向和最后一根径向的方位不一样,扫描区域往往出现重叠。相对于国内业务上常用的WSR-88D退速度模糊算法[23]仅仅从径向方向进行退速度模糊处理而言,新算法则是先进行方位角方向的处理,再进行径向方向的处理,因而方位角读取之后的处理是相当重要的,不适当的处理方式不仅会影响退模糊效果,也会在不同程度上改变原先的速度场数值。

|
图 5 雷达体扫径向位置示意图 Fig. 5 The radial location of VOL scan |
为解决这一问题,在读取数据后,做了径向归一化及补缺径向的处理,使得每一个方位角方向上都有且仅有一根径向速度数据。具体做法是:先读取雷达观测到的所有方位角值,同时除了记录实际径向数目的数组以外,再设置一个标准化的数组,把每层扫描后的径向都设置为360根。之后,对每根径向进行处理,比如处理第0根径向时,就对该仰角层的所有方位角值进行循环查找,找到与0相比数值上最接近的一个方位角值作为第0根径向的方位角数值,并同时把该方位角值原先对应的径向数目记为“1”,避免在其他径向处理时出现重复使用同一方位角数值的情况。这样处理之后,就会使得方位角分辨率为1,所有仰角层的径向都归一为360根,且每根径向上都有相应的方位角数值,这样就解决了径向速度数据重叠以及个别方位角上的径向速度数据会丢失的问题。相应地,原先的退速度模糊效果在一定程度上也有了改善。
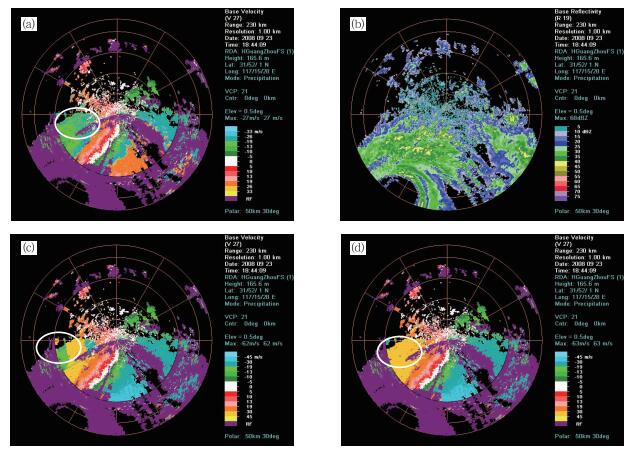
图 6给出该算法应用于2008年9月23日台风黑格比所得的结果。从图 6中可以看出,该个例在进行径向处理之后,之前被错误处理的大块区域都得到了正确修正,但被距离扩展区包围的个别散点出现了正确数据被错误处理的情况,不过这样的个别散点并不会影响整个雷达资料的使用。
|
图 6 2008年9月23日18:44台风黑格比广州站0.5°仰角层上的雷达径向速度资料(最大不模糊速度为26.32 m·s-1)(a)进行退速度模糊处理前的径向速度;(b)相应的强度场;(c)新算法原先退速度模糊处理后的径向速度;(d)新算法经过补缺径向处理再进行退速度模糊的径向速度 Fig. 6 Radial velocity field observed by Guangzhou radar on 0.5° tilt at 18:44 BT 23 Sept.2008. The Nyquist velocity for this case is 26.32 m·s-1 Shown in the figure are (a) raw, (b) the associated base reflectivity, (c) dealiased using the new algorithm, and (d) dealiased using the new algorithm after supplementing radials. The white circles indicate arcs of aliased velocity |
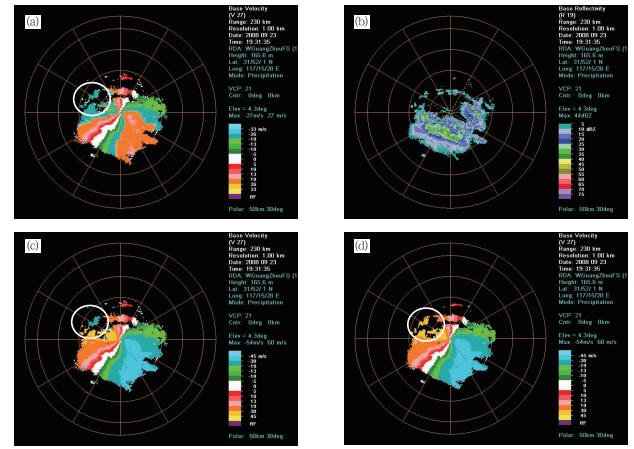
此外,台风径向速度场中,有很多强度较弱,且处于大片回波边缘区域的回波散点,这些散点对数据资料研究本身没有意义,且它们的存在可能会对退速度模糊处理产生一定影响,所以考虑去除部分回波散点。采用的方法是,在5×5区域内,计算有效点与该区域内所有点的比值,若小于0.6,则把区域内中间点赋为无效值。从图 7中可以看出,该方法能较好地去除散点,且能在很大程度上改善孤立回波以及回波边缘区退速度模糊的效果。
|
图 7 2008年9月23日19:31台风黑格比广州站4.3°仰角层上的雷达径向速度资料(最大不模糊速度为26.32 m·s-1)(a)进行退速度模糊处理前的径向速度;(b)相应的强度场;(c)新算法进行散点回波处理前的退速度模糊效果;(d)新算法经过散点回波处理后的退速度模糊效果 Fig. 7 Radial velocity field observed by Guangzhou radar on 4.3° tilt at 19:31 BT 23 Sept.2008. The Nyquist velocity for this case is 26.32 m·s-1. Shown in the figure are (a) raw, (b) the associated base reflectivity, (c) dealiased using the new algorithm, and (d) dealiased using the new algorithm after wiping off the discrete dots. The white circles indicate arcs of wiping off the discrete dots |
本文主要把新算法应用到国内台风(SA雷达)及冰雹、暴雨等对流性天气过程(CB雷达)的个例分析中。一方面,因为台风风速大,多出现速度模糊的情况,且国内特别是广东、浙江、福建等沿海地区受台风影响较为严重,更好地处理台风雷达径向速度资料,对分析研究台风有很重要的意义。另一方面,CB型号的雷达最大不模糊速度相对较小,且对流性天气过程中多有离散的、孤立的对流单体回波,这样退速度模糊的难度相应就会增加,如果对于这样的回波单体新算法能够有较好的退速度模糊效果,那在一定程度上即能说明新算法的有效性与准确率。在此基础上,如果新算法研究成熟,希望能进一步推广到业务应用中,这样对业务发展也有较大的实用价值。
本文分别选取了中等强度的台风个例、非常强的台风个例以及强对流风暴个例,选取了四个雷达站共277个台风雷达体扫基数据资料、四个雷达站共188个对流性天气过程雷达体扫基数据资料。采用的台风资料是2008年6月25日在深圳沿海登陆的台风风神广州站资料,2008年7月28日在福建福清市登陆的台风凤凰福州站和厦门站资料,以及2008年9月24日在广东电白陈村镇沿海登陆的台风黑格比广州站和阳江站资料。其中,“风神”和“凤凰”属于中等强度的台风个例,“黑格比”则属于非常强的台风个例。此外,采用的对流性天气过程雷达体扫基数据资料是2005年5月30日陕甘宁强对流风暴西安站资料,2006年6月24日北京雷暴大风过程张北站资料,2006年6月25日陕西强风暴天气西安站资料,以及2006年7月27日内蒙古强冰雹天气过程鄂尔多斯站资料。
2.1 个例分析为了更好地说明新算法的效果及特点,在个例分析中用目前国内业务中WSR-88D与98D上使用的退速度模糊算法与新算法做了对比。
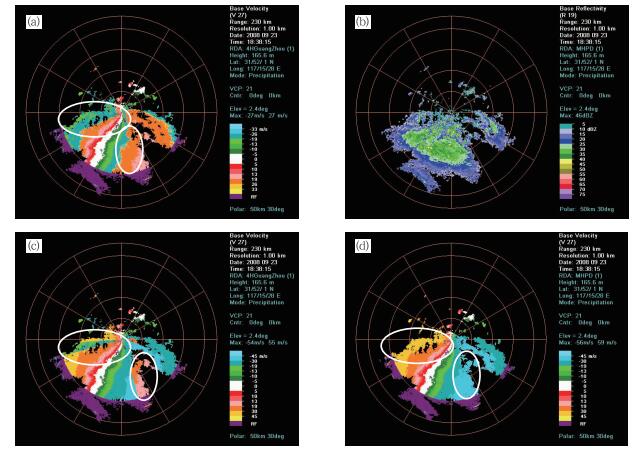
个例1,图 8给出了2008年9月23日台风黑格比广州站(SA雷达)2.4°仰角层上的径向速度资料,该资料中距离折叠较为严重,经过修正后有大片的距离扩展区,且风场较不连续。在图中可以看出,速度模糊区域出现在回波边缘部分且在该区域内同一方向上的同一根径向均是错误的速度值。WSR-88D算法是按径向方向处理速度模糊的,在径向上不能找到正确的速度参考值,自然就不能正确处理这样的速度模糊。新算法在退模糊过程中,首先退方位角方向,再退径向方向。在该个例中,虽然径向方向都是错误的速度值,但方位角方向却能找到正确的速度参考值,因而新算法能处理这样的速度模糊。这也是新算法在退速度模糊处理过程中的最大特点之一。
|
图 8 2008年9月23日18:38台风黑格比广州站2.4°仰角层上的雷达径向速度资料(最大不模糊速度为26.32 m·s-1)(a)进行退速度模糊处理前的径向速度;(b)相应的强度场;(c) WSR-88D算法的退速度模糊效果;(d)新算法的退速度模糊效果 Fig. 8 Radial velocity field observed by Guangzhou radar on 2.4° tilt at 18:38 BT 23 September 2008. The Nyquist velocity for this case is 26.32 m·s-1 Shown in the figure are (a) raw, (b) the associated base reflectivity, (c) dealiased using the operational WSR-88D scheme, and (d) dealiased using the new algorithm. The white circles indicate arcs of aliased velocity |
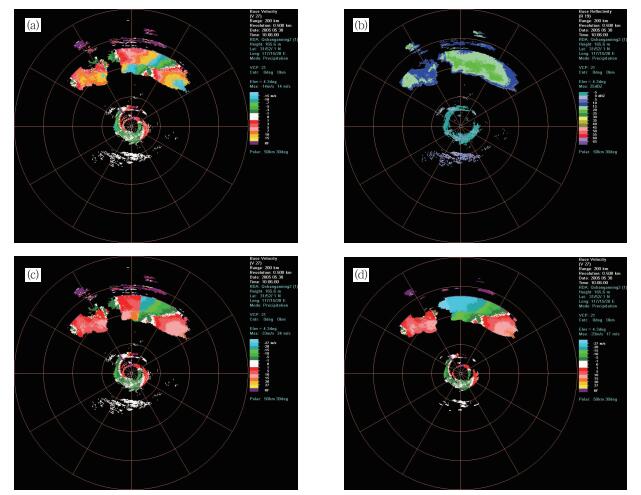
个例2,图 9给出了陕甘宁强对流风暴西安站(CB雷达)4.3°仰角层上的雷达径向速度资料。该资料中除了连续性风场,也有孤立回波的速度模糊。对于这样的孤立强对流回波单体,且最大不模糊速度也相对较小的情况,退速度模糊难度往往会增加。
|
图 9 2005年5月30日10:06陕甘宁强对流风暴西安站4.3°仰角层上的雷达径向速度资料(最大不模糊速度为13.99 m·s-1)。(a)进行退速度模糊处理前的径向速度;(b)相应的强度场;(c) WSR-88D算法的退速度模糊效果;(d)新算法的退速度模糊效果 Fig. 9 Radial velocity field observed by Xi'an radar on 4.3° tilt at 10:06 BT 30 May 2005. The Nyquist velocity for this case is 13.99 m·s-1 Shown in the figure are (a) raw, (b) the associated base reflectivity, (c) dealiased using the operational WSR-88D scheme, and (d) dealiased using the new algorithm. The white circles indicate arcs of aliased velocity |
该个例中,东北方向的那一大块回波是连续性风场,并且这块回波速度模糊情况比较严重,从图中可以看到它有一个并不是很明显的零速度线,以此零速度线为带,往右区域是由最大正速度突变为最大负速度;往左区域是由最大负速度突变为最大正速度。可见,往右及往左各有一块回波模糊,因此虽然模糊比较严重,但并没有出现二次模糊的情况。
对于这样严重的速度模糊情况,一般较难寻找到合适的参考速度初值,因而退速度模糊处理很容易出错。对新算法来说,因为会从径向和方位角两个方向同时进行退速度模糊处理及错误检查,并且在第一轮退速度模糊之后,对没有被正确处理的数据再进行第二次处理,这样的处理步骤能使得错误减少到最低,所以对于这样的速度场,新算法同样能有很好的退速度模糊效果。
然而,对于一块完全错误的孤立回波单体而言,因为缺乏正确的速度参考值,新算法和其他软件退模糊算法一样,也会存在问题。该个例中西北方向的一块孤立回波几乎全是正速度值,但根据该个例的风场情况以及前后相邻时刻的数据速度场的分析,认为西北部分的回波应为西北风,所以这块回波应该都为正速度,而新算法也没能正确处理这部分回波。造成这种错误,是因为新算法对于孤立回波也只能利用回波内部的数据来进行分析处理,而无法利用到相邻回波的数据。
孤立回波的速度模糊问题,一直以来是退速度模糊的难点问题之一。新算法也存在一定的弊端,希望今后能找到更合适的方法,解决这个问题。
经过个例分析,认为新算法在参考径向的寻找以及具体处理过程方面具备一定的特点,因而在处理台风及对流性天气过程径向速度模糊方面效果较好,不仅能有效地处理连续性风场的径向速度模糊,而且当速度场存在大量的数据缺失、不连续性以及距离折叠时,同样也能有较好的退速度模糊效果。然而,不可避免地,新算法也会存在一些问题,它能正确处理的回波也主要是大范围的速度模糊区域,对于孤立的、离散的强对流回波单体的退速度模糊处理,有时也会失效。
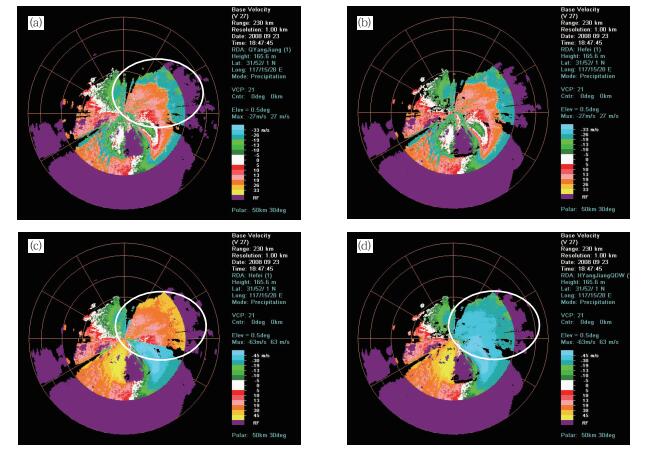
2.2 地物回波对退速度模糊效果的影响图 10是2008年9月23日台风黑格比阳江站0.5°仰角层的径向速度资料,新算法没能正确地对该资料进行退速度模糊处理。在分析原因时发现,除了风速太大之外,地物回波也可能是影响退速度模糊效果的原因之一。在低层仰角,地物回波较多,当出现速度模糊且径向风速较大时,在模糊区域若有地物回波,地物回波与相邻距离库之间的速度值之差往往会超过模糊判断阈值,则容易出现误判导致退速度模糊处理出错。
|
图 10 2008年9月23日18:47台风黑格比阳江站0.5°仰角层上的雷达径向速度资料(最大不模糊速度为26.32 m·s-1)(a)未经过任何处理的原始径向速度;(b)去地物回波后的径向速度;(c)去地物回波之前新算法的退速度模糊效果;(d)去地物回波之后新算法的退速度模糊效果 Fig. 10 Radial velocity field observed by Yangjiang radar on 0.5° tilt at 18:47 BT 23 September 2008. The Nyquist velocity for this case is 26.32 m·s-1 Shown in the figure are (a) raw, (b) radial velocity before echo classify, (c) dealiased using the new algorithm before echo classification, and (d) dealiased using the new algorithm after echo classification. The white circles indicate arcs of aliased velocity |
根据这个想法,对于径向风速较大且低层仰角地物回波较多的资料,利用模糊逻辑法[24]进行了去除地物回波处理,之后再用新算法进行退速度模糊处理,发现退速度模糊效果有较大改观(图 10)。2008年9月23日台风黑格比阳江站30个雷达体扫基数据中,0.5°、1.5°、2.4°仰角层地物回波较多。表 1分别给出了新算法进行地物回波处理前后以及WSR-88D算法对这些体扫基数据共90个仰角层的退速度模糊处理结果,可见地物回波也是影响退速度模糊效果的原因之一。
|
|
表 1 去地物回波前后退速度模糊的准确率(单位:%) Table 1 Accuracy of velocity dealiasing before and after echo classification (unit: %) |
Zhang提出的二维多途径退速度模糊方法能够在径向速度场中自动寻找参考速度值,同时进行两轮退速度模糊处理。在第一轮处理中寻找参考速度值的方法是相当严格的,以确保尽可能地处理模糊速度,获取正确的实际速度值。在第一轮中被正确处理的速度值在第二轮处理中会被认为是好的距离库而作为参考值进行退速度模糊。这种方式很大程度上提高了退速度模糊算法的可靠性与准确性。
不同于WSR-88D退速度模糊算法,新算法在处理速度模糊时从方位角和径向两个方向同时进行处理,且雷达进行体积扫描时,扫描区域往往出现重叠现象,因而,径向读取及处理方式对于新算法退速度模糊的效果也是相当重要的,文中在读取方位角数据之后,做了径向归一化及补缺径向的处理,经过处理,使得所有仰角层的径向都归一为360根,且每根径向上都有相应的方位角数值,这样就解决了径向速度数据重叠以及个别方位角上的径向速度数据会丢失的问题。此外,去除了强度较弱,且处于大片回波边缘区域的回波散点。这些处理在一定程度上改善了退速度模糊的效果,对于新算法的推广应用也是相当重要的。
本文把该算法应用到我国新一代天气雷达(SA、CB)观测的台风、强对流风暴资料质量控制中发现,该算法不仅能处理连续性风场的速度模糊,也能处理存在大量数据缺失以及距离折叠的不连续性风场的径向速度模糊,但对于孤立回波的速度模糊的处理,也会出现问题。同时,分析了地物回波对退速度模糊效果可能的影响。
不可避免地,二维多途径退速度模糊算法也存在一定的弊端, 且多普勒天气雷达的速度模糊问题,是多年来一直影响风场信息应用的棘手问题,但退速度模糊技术有非常重要的现实意义。因此,在今后的工作中,除了将提出自动检查判断退速度模糊效果的方法以外,进一步研究新算法,找出新算法对于一些资料不能正确处理的原因,并寻求解决方案以更好地完善算法是非常必要的。
| [1] |
刘淑媛, 王洪庆, 陶祖钰, 等. 一种简易的多普勒雷达速度模糊纠正技术[J]. 应用气象学报, 2003, 14(5): 111-116. |
| [2] |
万蓉, 郑国光, 王斌, 等. 利用多普勒雷达速度资料检验三维中小尺度模式流场[J]. 气象, 2009, 35(1): 3-8. DOI:10.7519/j.issn.1000-0526.2009.01.001 |
| [3] |
牟容, 刘黎平, 许小永, 等. 四维变分方法反演低层风场能力研究[J]. 气象, 2007, 33(1): 11-18. DOI:10.7519/j.issn.1000-0526.2007.01.002 |
| [4] |
牛淑贞, 潘新民, 杨洪平, 等. 《新一代天气雷达灾害性天气警报和临近预报系统》应用[J]. 气象, 2009, 35(5): 105-111. DOI:10.7519/j.issn.1000-0526.2009.05.015 |
| [5] |
樊利强, 王迎春, 陈明轩. 利用雷达资料反演方法对背景地区一次强对流天气过程的分析[J]. 气象, 2009, 35(11): 9-16. DOI:10.7519/j.issn.1000-0526.2009.11.002 |
| [6] |
王国荣, 卞素芬, 王令, 等. 用地面加密自动观测资料对北京地区一次飑线过程的分析[J]. 气象, 2010, 36(6): 59-65. DOI:10.7519/j.issn.1000-0526.2010.06.009 |
| [7] |
李向红, 唐熠, 郑传新, 等. 一次多种强对流天气过程的雷达回波特征分析[J]. 气象, 2010, 36(8): 61-71. DOI:10.7519/j.issn.1000-0526.2010.08.009 |
| [8] |
杨丹丹, 申双和, 邵玲玲, 等. 雷达资料和数值模式产品融合技术研究[J]. 气象, 2010, 36(8): 53-60. DOI:10.7519/j.issn.1000-0526.2010.08.008 |
| [9] |
冯晋勤, 汤达章, 俞小鼎, 等. 新一代天气雷达中气旋识别产品的统计分析[J]. 气象, 2010, 36(8): 47-52. DOI:10.7519/j.issn.1000-0526.2010.08.007 |
| [10] |
张少波, 陆汉城, 张鹏, 等. 基于MVAD技术的多普勒雷达径向速度退模糊方法的改进研究[J]. 热带气象学报, 2007, 23(5): 497-504. |
| [11] |
Ray P, Ziegler C. De-aliasing first-moment Doppler estimates[J]. J of App Meteor, 1977, 16: 563-564. DOI:10.1175/1520-0450(1977)016<0563:DAFMDE>2.0.CO;2 |
| [12] |
Bargen D W, R C Brown. Interaction radar velocity unfolding[G]. Proc 19th Conference on Radar Meteorology, Miami, FL., Amer Meteor Soc, Boston, 1980:278-283.
|
| [13] |
Merrit M W. Automatic velocity dealiasing for real-time application[G]. 22nd Conference on Radar meteorology, Zurich, Switzerland, Amer Meteor Soc, Boston, 1984. 528-533.
|
| [14] |
Boren T A, Cruz J R, Zrnic D S. An artificial intelligence approach to Doppler radar velocity dealiasing[G]. 23rd Conference on Radar Meteorology, Snowmass, Colo., Amer Meteor Soc, Boston, 1986:107-110.
|
| [15] |
Bergen W R, Albers S C . Two-and three-dimensional de-aliasing of Doppler radar velocities[J]. Journal of Atmospheric and Oceaic Technology, 1988, 5: 305-319. DOI:10.1175/1520-0426(1988)005<0305:TATDDA>2.0.CO;2 |
| [16] |
Eilts M D, Smith S D . Efficient dealiasing of Doppler velocities using local environment constraints[J]. Journal of Atmospheric and Oceanic Technology, 1990, 7: 118-128. DOI:10.1175/1520-0426(1990)007<0118:EDODVU>2.0.CO;2 |
| [17] |
James C N, R A H JR. A real-time four-dimensional Doppler dealiasing scheme[J]. Journal of Atmospheric and Oceanic Technology, 2001, 18: 1674-1683. DOI:10.1175/1520-0426(2001)018<1674:ARTFDD>2.0.CO;2 |
| [18] |
Tabary P, Scialom G. Real-time retrieval of the wind from aliased velocities measured by Doppler radars[J]. Journal of Atmospheric and Oceanic Technology, 2001, 18: 875-882. DOI:10.1175/1520-0426(2001)018<0875:RTROTW>2.0.CO;2 |
| [19] |
Gao J, Droegemeier K K, GONG J, et al. A method for retrieving mean horizontal wind profiles from single-Doppler radar observations contaminated by aliasing[J]. Monthly Weather Review, 2004, 132: 1399-1409. DOI:10.1175/1520-0493-132.1.1399 |
| [20] |
Haase G, Landelius T. Dealiasing of Doppler radar velocities using a torus mapping[J]. Journal of Atmospheric and Oceanic Technology, 2004, 21: 1566-1573. DOI:10.1175/1520-0426(2004)021<1566:DODRVU>2.0.CO;2 |
| [21] |
梁海河, 张沛源, 葛润生. 多普勒天气雷达风场退模糊方法的研究[J]. 应用气象学报, 2002, 13(5): 591-601. |
| [22] |
Zhang J, Wang S. An automated 2D multipass Doppler radar velocity dealiasing scheme[J]. Journal of Atmosperic and Oceanic Technology, 2006, 23: 1239-1248. DOI:10.1175/JTECH1910.1 |
| [23] |
俞小鼎, 姚秀萍, 熊廷南, 等. 多普勒天气雷达原理与业务应用[M]. 北京: 气象出版社, 2006: 82-86.
|
| [24] |
刘黎平, 吴林林, 杨引明. 基于模糊逻辑的分布式超折射地物回波识别方法的建立和效果分析[J]. 气象学报, 2007, 65(2): 252-260. DOI:10.11676/qxxb2007.024 |
 2011, Vol. 37
2011, Vol. 37 