在过去的几十年中, 大气温度、湿度等廓线的反演已经取得一定进展, 然而其精度并没有达到数值天气预报的要求, 主要原因有两个:第一, 目前业务上使用的是多分辨率的红外垂直探测器, 受遥感技术水平限制, 光谱分辨率较低, 反演精度和分辨率不如人意。小尺度的垂直结构很难反演[1], 是当前反演面临的一大难题。解决这一问题的办法在于发展高光谱分辨率的红外垂直探测仪器。第二, 反演处理上存在的一些问题以及大气透过率计算的误差, 下垫面的一些未知因素, 云的影响等。解决办法是提高大气透过率计算精度, 发展一套高效率的反演算法。由于反演问题是一个非适定性问题, 即其解不唯一、不稳定, 必须在求解过程中增加一些附加条件后才能得到一个稳定解。
美国地球观测系统EOS(Earth Observing System)第二颗卫星Aqua上的大气红外探测仪(AIRS)是一个高光谱红外垂直探测器, 它可以实现的光谱分辨率达到了分辨大气成分单个谱线的水平, 使大量通道同时遥感反演大气温、湿廓线成为可能[2]。目前国内基于AIRS资料反演大气温度、湿度垂直廓线大多采用的是特征向量统计反演法, 该方法本质是一种基于最小二乘法的统计回归算法[3]。神经网络是一个由大量简单的处理单元组成的高度复杂的大规模非线性自适应系统, 可以实现输入空间到输出空间的非线性映射。20世纪80年代中期以来, 神经网络的应用研究取得了很大的成就, 涉及面非常广泛。误差反传算法, 即BP算法(Back Propagation), 已成为至今影响最大、应用最广泛的一种网络学习方法[4]。20世纪90年代, 国内外在气象学科中开展了很多有关神经网络预报建模和气候分析等应用的研究[5-6], 在中、长期天气预报应用中也有不少成功的例子[7]。近几年来, 人工神经网络已经应用于降雨的预报[8]、AMSU-A(Advanced Microwave Sounding Unit-A, 先进的微波垂直探测器)仪器微波观测资料的反演[9]以及数值预报产品的释用[10]。基于AIRS高光谱资料采用神经网络法进行模拟资料的晴空大气温度廓线反演, 较之特征向量统计法, 各高度层精度均有不同改进, 获得了较好的反演结果[11, 19];而实况资料的温度廓线反演, 神经网络法的反演精度并没有明显提高[12], 原因之一是所选的神经网络结构并不是泛化性能最佳的网络。本文尝试用人工神经网络法反演大气湿度廓线, 着重优化网络结构, 以提高精度, 提高适用性。
1 训练样本样本是由全球晴空反演训练样本廓线和相应的SARTA模式模拟的亮温值组成样本对。CIMSS(Cooperative Institute for Meteorological Satellite Studies, University of Wisconsin-Madison, 气象卫星合作研究所, 威斯康星大学麦迪逊分校)全球晴空反演训练样本集由TIGR3(TOVS Initial Guess Retrieval, 泰罗斯业务垂直探测器初始猜测回归场)、NOAA-88 (National Oceanic and Atmospheric Administration, 美国国家海洋和大气局)和ECWMF (European Center of Medium-range Weather Forecasts, 欧洲中期天气预报中心)等全球有代表性的温、湿和臭氧等廓线组成, 同时还补充了沙漠地区的无线电探空和臭氧探空值, 所有廓线从1100 hPa到0.005 hPa被内插到101个气压层, 共12208条廓线样本, 并按IGBP(International Geosphere-Biosphere Programme, 国际地圈生物圈计划)生态系统进行分类, 其中15个红外通道的地表比辐射率由与生态系统相关的MODIS(moderate-resolution imaging spectroradiometer, 中分辨率成像光谱仪)(MOD11) 产品得到。廓线地区分布在海洋上较稀疏, 在大陆上较发达地区分布密集, 如图 1。对全球晴空反演训练样本集使用SARTA v1.05版的前向模式(该软件包是AIRS-RTA大气红外探测器辐射传输算法的实际应用, 是一个用于计算AIRS辐射传输值的快速前向模式)模拟出AIRS辐射亮温值。如果前向模式的精度能达到仪器噪声的水平, AIRS具有的高光谱分辨率及低噪声的特性可使得到与现有的世界上业务无线电探测网络相媲美或更精确的大气廓线。

|
图 1 12208条廓线全球分布情况 Fig. 1 The global distribution of 12208 profiles |
神经网络是一个由大量简单的处理单元组成的高度复杂的大规模非线性自适应系统, 具有良好的学习功能。它可以接受用户提交的样本集合, 依照系统给定的算法, 不断地修正用来确定系统行为的神经元之间连接的强度, 并存放于系统中。
神经网络包含许多网络模型, BP算法是应用最为广泛的多级网络训练算法。BP神经网络的基本原理是, 网络得到输入以后, 经过加权并通过各层激励函数的计算得到输出层的输出值。将这个值与期望值做比较, 如果均方根误差在理想范围内, 则认为网络学会这一问题, 停止训练, 保存网络的权值, 建立该网络;如果均方根误差未达到预期值则把误差反向传播, 根据误差修改各连接权重, 进行下次训练。如此反复, 直到网络输出期望输出的均方根误差达到预期标准。
相对传统的数理统计方法而言, BP神经网络可以求解非线性问题, 同样对样本大小的要求也可以相对少得多(如果样本能够代表该问题的各种类型特征), 并不要求样本独立或遵从正态分布, 还具有较强的容错能力, 即网络系统的判别精度一般不受样本中噪声的影响。
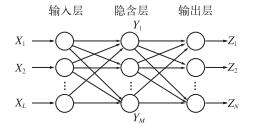
2.1 BP网络的设计BP网络可有效地用于复杂的非线性函数的逼近, 一个3层的前馈网络能够实现任意精度的连续函数映射[13]。BP网络模型见图 2。
|
图 2 BP网络模型示意图 Fig. 2 BP network model diagram |
为提高反演的精度, 将训练样本根据波数1000 cm-1(窗区)时的亮温温度分成6类, 分别训练网络, 反演时不同亮温分类采用不同的网络。表 1给出亮温分类每类阈值。为减少错误分类的影响, 亮温分类时每类的阈值重叠了10 K[14]。
|
|
表 1 亮温温度分类方案 Table 1 The classification scheme of brightness temperature (K) |
为确保模拟的真实性, 在进行反演前, 需要给计算的辐射值增加些模拟的AIRS仪器噪音。噪音根据高斯分布随机产生, 平均值取零, 标准差为AIRS通道特性文件中的NEΔT(Noise Equivalent Delta Temperature, 等同于250 K亮度温度时噪音值)。
2.4 主特征分析的应用主成分分析方法PCA(Principal Component Analysis)是系统降维和特征提取的一种基本方法。研究表明, 对AIRS的2378个通道的观测值取其前30个主成分可以代表 99.9988%的所有AIRS的信息量[14]。因此, 在我们研究中, 就选取前30个主成分。
将经过主成分分析之后的数据应用于大气温湿廓线反演具有明显的优越性:(1) 直接去除特征值为零或接近于零的特征值对应的主分量。(2) 只保留与反演量相关程度高的主分量, 降维作用直观显著。(3) 由于主分量间是正交的, 所以不会有多余的重复信息噪声影响。
2.5 输入输出强欠定问题的处理由于我们选取前30个主成分作为输入, 101层湿度廓线作为输出, 造成了网络结构的强欠定性, 会使得网络的训练预测能力下降。这里采取一种方法, 将作为输出的101层湿度廓线进行分段, 分段依据特征向量统计法反演的水汽混合比相对于真值的均方根误差RMSE(Root Mean Square Error)曲线。如图 3所示:可以看出, 从近地面到800 hPa处, RMSE约为2;从800 hPa到600 hPa处, RMSE约为1;从600 hPa到接近250 hPa处, RMSE小于1;250 hPa以上的高空, RMSE几乎为0。因此将101层湿度廓线分成4段(如表 2)。

|
图 3 特征向量统计法反演的水汽混合比与真值的均方根误差曲线 Fig. 3 The root mean square error curve between the true value of water vapor mixing ratio and the value retrieved by eigenvector statistics |
|
|
表 2 廓线分段方案 Table 2 The plan of the profile section |
由此可见, 分段以后除了第一段的变量数仍大于输入以外, 其他三段的输出均少于输入。经验证, 这样分段训练, 不仅提高了训练精度, 并且大大地节省了训练时间。需要指出的是, 这里的分段方案只是根据经验, 综合考虑网络训练的精度与速度而制定的一种分类方案, 并不一定是最优方案。
2.6 过拟合问题的处理衡量网络训练的性能好坏依据MSE(Mean Square Error, 均方差)这个参量。一般来讲, MSE越小, 网络训练的精度越高。但是, 神经网络很容易出现过拟合现象, 即网络训练到一定程度时, 随着训练的能力提高, 预测的能力反而下降。不仅浪费时间, 而且最终结果可能也达不到要求, 解决这个问题的一种办法是:在数据输入中, 给训练的数据分类, 分为正常训练用、变量数据、测试数据, 三种数据的比例这里采用60%、20%、20%。为避免相邻的样本具有相关性, 每5个样本中选取1个作为变量数据, 1个作为测试数据, 3个作为训练数据。在网络训练的时候监测Validation Checks这个参量, 设定一个阈值。当训练网络过程中该参量达到阈值, 则停止训练。BP算法很有可能陷入局部极值, 使训练失败。如果停止训练后, 网络训练没有达到预期的精度, 则重新训练, 直到网络训练达到目标精度为止。
2.7 激活传递函数的选取激活函数是一个神经元及网络的核心。网络解决问题的能力与功效除了与网络结构有关, 在很大程度上取决于网络所采用的激活函数。激活函数的输入为神经元输入矢量的加权和。经试验, 二层均选取双曲正切S型函数:tansig。网络输出的计算公式为:
| $ \mathit{\boldsymbol{A}} = {\rm{tansig}}\left( {\mathit{\boldsymbol{W}} \times \mathit{\boldsymbol{P}} + \mathit{\boldsymbol{B}}} \right) $ | (1) |
其中, W为权值, P为输入矢量, B为偏差。
2.8 隐节点数的选取三层的BP网络中有一层隐含层, 当隐含层神经元数目足够多时, 可以以任意精度逼近任何一个具有有限间断点的非线性函数。隐含层节点数的设置关系到网络性能的好坏。怎样确定隐含层中适宜的神经元个数使模型的泛化能力最大, 至今没有很好的结论[15-16]。隐节点数太少会造成信息不足, 造成网络训练达不到要求;太多会造成浪费, 使训练时间加长。在试验中发现, 针对不同的样本, 即使输入层输出层节点数相同, 网络收敛最快的隐节点数值也可能会不同。输入输出层节点数均相同的二组数据, 隐节点的选取和当时的网络初始权值也有关系。最后根据前人经验计算的数值作为参考值, 缩小选取隐节点数的区间。以不同的网络初始权值多次训练网络, 同时更改隐节点数, 以求达到较高的训练精度。
2.9 训练算法的选取在选择算法对网络进行训练的时候, 在网络参数很多, 需要考虑存储容量问题时, 选择共轭梯度法[17]。经试验, 这里选择Scaled共轭梯度法trainscg。该算法区别于其他算法的参数有sigma缺省设置为5e-005, lambda缺省设置为5e-007。
3 反演结果 3.1 与特征向量统计反演法湿度反演结果比较特征向量统计法是一种线性的、统计的算法[18]。而BP网络是通过误差不断地反传来调整权值, 使得最终的网络输出与真值的误差达到预期要求。神经网络法是一种非线性的方法, 在非线性函数拟合上, 理论上要优于特征向量统计法。
采用上述全球12208个训练样本, 间隔选取8138个样本进行训练, 其他4070个样本用于独立的反演检验。分别用人工神经网络算法(简称NNW)和特征向量统计方法(简称ESW)进行反演, 将得到的结果与样本真值进行比较, 计算均方根误差RMSE。
RMSE误差定义为:
| $ RMSE = \sqrt {\frac{1}{{{N_S}}}\sum\limits_{i = 1}^{{N_S}} {{{\left( {{X_{{\rm{RAOB}}}}-{X_{{\rm{AIRS}}}}} \right)}^2}} } $ | (2) |
其中XRAOB和XAIRS分别是样本廓线及AIRS反演的参数值, NS是样本个数。
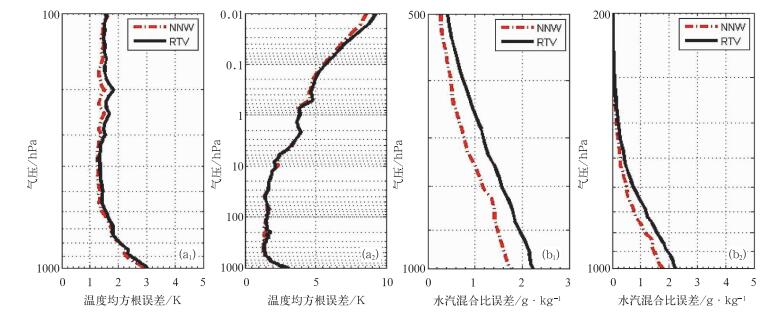
图 4a是反演的温度均方根误差, 图a1为图a2的局部。图 4b是反演的水汽混合比均方根误差, 图b1为图b2的局部。从图 4a可以看出, 在温度反演问题上, 神经网络法反演的结果略优于特征向量统计法, 但效果不明显。从图 4b可以看出, 神经网络法反演的结果在所有的气压层上都要优于特征向量统计法的结果。在近地面到500 hPa层面, 这种优势更加明显。改进的最大值为0.7926 g·kg-1, 近地面到500 hPa平均改进值大于0.4 g·kg-1。
|
图 4 (a)温度均方根误差(图a1为图a2的局部); (b)水汽混合比均方根误差(图b1为图b2的局部) Fig. 4 The RMS errors of temperature (a, K) and water vapor mixing ration (b, g·kg-1) In Fig.4a and Fig.4b, the left figure is the detailed part of the right figure |
由于训练样本是从全球样本中挑出, 并没有考虑它不同的下垫面情况、地形、地表辐射等, 以及区域气候。采用全球样本训练是为了使训练好的网络可以推广到全球范围的反演。可以预见, 若想反演某一区域的大气廓线, 可以采用该区域的样本训练网络, 以达到更精确的结果。
3.2 湿度廓线的拟合为判断两种反演方法的拟合情况, 将上述湿度反演均方根误差RMSE分成4类:
(1) 两种廓线的拟合情况均理想。从近地面到200 hPa的高空这近50个气压层, 平均每层与真值的绝对误差小于0.15 g·kg-1, 有483条廓线。
(2) 两种廓线的拟合情况均不理想。从近地面到200 hPa的高空这近50个气压层, 平均每层与真值的绝对误差大于1.5 g·kg-1, 有253条廓线。
(3) 神经网络法的反演结果优于特征向量统计法的反演结果。这类廓线是除去前二类之外二种方法进行比较所得, 有2303条廓线。
(4) 特征向量统计法的反演结果优于NNW, 共有1031条廓线。
这4种情况的廓线分布如图 5a~5d。图 5a第一类廓线分布, 发现这些点大都集中在高纬度地区。图 5b是第二类廓线分布, 发现这些点大都集中在山地, 或者赤道附近。由于山地下垫面复杂, 地表比辐射率复杂;赤道水汽含量多, 增加了反演的难度。图 5c是第三类廓线分布情况, 图 5d则是第四类廓线分布。后两幅图的廓线分布从直观上看并未发现有什么明显特征。

|
图 5 第一类廓线分布(a); 第二类廓线分布(b); 第三类廓线分布(c); 第四类廓线分布(d) Fig. 5 The profile distribution of (a) the first kind, (b) the second kind, (c) the third kind, and (d) the fourth kind |
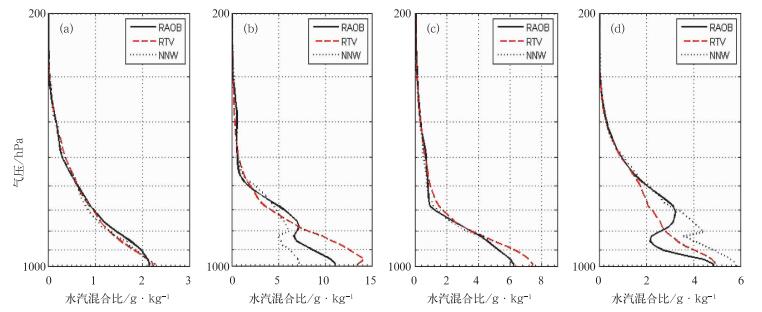
在以上4类廓线中, 任取一条为例, 如图 6a~6d所示。这4条廓线101个气压层的RMSE见表 3。其中RTV RMSE表示特征向量统计法反演结果与真值比较所得的均方根误差, NNW RMSE表示神经网络法反演结果与真值比较所得的均方根误差。由这4幅图可以看出, 经特征向量统计法反演所得的廓线都比较平滑, 当真实廓线波动较大时, 拟合效果比较差。图 6b、6d虽然神经网络法拟合的廓线的RMSE不是很理想, 但是本方法的廓线很好地拟合出了真实廓线的走向。
|
图 6 第一类廓线拟合(a); 第二类廓线拟合(b); 第三类廓线拟合(c); 第四类廓线拟合(d) Fig. 6 The profile fitting of (a) the first kind, (b) the second kind, (c) the thrid kind, and (d) the fourth kind |
|
|
表 3 4条廓线的RMSE Table 3 The RMSE of four kinds of profiles |
本文基于AIRS模拟资料, 尝试使用神经网络法反演大气湿度廓线, 较之特征向量统计法, 本方法提高了反演精度, 并且神经网络法更能揭示真实大气湿度廓线的细微结构。
理论上, 一个3层的BP网络可以以任意精度逼近一个非线性函数。但是在实际应用中, 尤其是这种多输入、多输出大量样本的情况下很难达到这种程度。本文针对网络过拟合的情况采取了对训练数据分类, 在训练中监控某些参量, 避免过拟合的发生。另外, 采取气压层分段训练也解决了方程强欠定性问题, 提高了训练精度, 节省了训练时间。
由于样本数量庞大, 怎样集中选取代表性的样本, 这也是个值得思考的问题。如果选取得当, 将缩短训练时间, 提高训练精度。另外, 由于没有考虑地形、地表辐射以及区域气候等因素, 故个别廓线的反演上出现较大的误差。下一步将开展关于实况资料的反演及地形因子的订正等方面的研究, 期待神经网络法带给我们更好的表现。
| [1] |
蒋德明, 董超华, 陆维松. 利用AIRS观测资料进行红外高光谱大气探测能力试验的研究[J]. 遥感学报, 2006, 10(4): 586-592. DOI:10.11834/jrs.20060486 |
| [2] |
官莉. 星载红外高光谱资料的应用[M]. 北京: 气象出版社, 2007: 29.
|
| [3] |
Guan L, Huang H L, Li J. A study on retrieving atmospheric profiles from EOS/AIRS observations[J]. Acta Meteor Sinica, 2005, 19(1): 112-119. |
| [4] |
吴建生, 周优军, 金龙. 神经网络及其研究进展[J]. 广西师范学院学报(自然科学版), 2005, 22(1): 92-93. |
| [5] |
金龙, 况雪源, 黄海洪, 等. 人工神经网络预报模型的过拟合研究[J]. 气象学报, 2004, 62(1): 62-70. DOI:10.11676/qxxb2004.007 |
| [6] |
覃志年, 金龙, 况雪源. 人工神经网络的短期气候定性预测方法研究[J]. 气象科技, 2004, 32(3): 168-172. |
| [7] |
陈宁, 金龙, 袁成松. 最优子集的神经网络预报建模研究[J]. 气象, 1999, 25(1): 14-19. DOI:10.7519/j.issn.1000-0526.1999.01.003 |
| [8] |
李永华, 刘德, 金龙. 基于BP神经网络的汛期降水预测模型研究[J]. 气象科学, 2002, 22(4): 461-467. |
| [9] |
Yao Zhigang, Chen Hongbin, Lin Longfu. Retrieving atmospheric temperature profiles from AMSU-A data with neural networks[J]. Advances in Atnisogeruc Sciences, 2005, 22(4): 606-616. |
| [10] |
钱莉, 兰晓波, 杨永龙. 最优子集神经网络在武威气温客观预报中的应用[J]. 气象, 2010, 36(5): 102-107. DOI:10.7519/j.issn.1000-0526.2010.05.015 |
| [11] |
张雪慧, 官莉, 王振会, 等. 利用人工神经网络方法反演大气温度廓线[J]. 气象, 2009, 35(11): 137-142. DOI:10.7519/j.issn.1000-0526.2009.11.018 |
| [12] |
官莉, 刘旸, 张雪慧. 人工神经网络算法在红外高光谱资料反演大气温度廓线中的应用[J]. 大气科学学报, 2010, 33(3): 341-346. |
| [13] |
袁曾任. 人工神经网络及其应用[M]. 北京: 清华大学出版社, 1999.
|
| [14] |
官莉. 卫星红外超光谱资料及其在云检测、晴空订正和大气廓线反演方面的应用[D]. 博士论文, 2005, 46, 57. http://www.doc88.com/p-9873418678098.html
|
| [15] |
Wu Yan, Zhang Liming. A new regularization learning method for improving generalization capability of neuralnetwork[R]. Proceedings of 4th World Congress on Intelligent Control and Automation.Shanghai, 2002, 3: 2011-2015. http://doi.acm.org/10.1145/521706
|
| [16] |
江学军, 唐焕文. 前馈网络泛化性能力的系统分析[J]. 系统工程理论与实践, 2000, 20(8): 36-40. |
| [17] |
丛爽. 面向MATLAB工具箱的神经网络理论与应用[M]. 合肥: 中国科学技术大学出版社, 2003.
|
| [18] |
官莉. 利用AIRS卫星资料反演大气廓线Ⅰ.特征向量统计反演法[J]. 南京气象学院学报, 2006, 29(6): 757-758. |
| [19] |
周非非, 周毓荃, 王俊, 等. FY-2卫星反演的云顶高度与多普勒雷达回波顶高的关系初探[J]. 气象, 2010, 36(4): 43-50. DOI:10.7519/j.issn.1000-0526.2010.04.008 |
 2011, Vol. 37
2011, Vol. 37 