2. 国家气象中心,北京 100081;
3. 中国气象局,北京 100081;
4. 四川省气象台,成都 610000
2. National Meteorological Center, Beijing 100081;
3. China Meteorological Administration, Beijing 100081;
4. Meteorological Observatory of Sichuan Province, Chengdu 610000
近年来,以提高灾害性强降水预报准确率为目的的区域集合预报已成为一个研究热点[1-5]。GRAPES(Global/Regional Assimilation and Prediction System)模式[6]是我国自主研发的数值预报模式,已有部分研究工作表明:GRAPES模式对灾害性强降水表现出较好的预报性能[7-8]。GRAPES模式集合预报技术一直受到我国数值预报研究人员的重视。谭燕等[9]利用增长模繁殖法(BGM)[10],开展了区域GRAPES模式集合预报技术研究。试验结果表明:获取正确的初值扰动场信息,对构造有效的区域集合预报系统是有帮助的,集合预报能够在一定程度上提高灾害性暴雨降水的预报能力。王太微开展了GRAPES-BGM和GRAPES-ETKF两套区域集合预报系统的比较试验。结果显示:GRAPES-BGM和GRAPES-ETKF的集合平均预报结果均好于控制预报,降水预报效果与实况较接近。但是,在构造区域GRAPES集合预报系统方面还有一些问题值得进一步研究,包括:怎样正确反映GRAPES模式的不确定性特征?如何更好地构造GRAPES模式的初值扰动方法,特别是如何充分利用全球集合预报系统提供的初始扰动场信息,增加GRAPES集合预报系统的发散度等问题,还需要进一步开展深入研究。
近年来,世界气象组织(WMO)在THORPEX(THe Observing system Research and Predictability EXperiment,全球观测系统研究和可预报性试验)科学计划下成功实施了全球交互式大集合预报系统(THORPEX Interactive Grand Global Ensemble,简称TIGGE)。TIGGE是一个全球各国家和地区的业务数值预报中心的联合行动,它将各主要业务中心集合预报产品集中到一起,示范并评价多模式、多分析和多国集合预报系统。TIGGE数据库储存了各国家集合预报系统的分析和预报结果。WMO设立了三个TIGGE资料中心,中国气象局(CMA)与欧洲中期天气预报中心(ECMWF)和美国环境预报中心(NCEP)一起作为TIGGE资料交换的三个全球中心,从2006年开始我国逐步进入全球交互式大集合TIGGE计划当中,成立了TIGGE中国中心,并建立了相应的专家组和工作小组,开始全面负责实施中国TIGGE计划的推进工作,2007年中国气象局建立了TIGGE资料库,并初步实现了资料的实时接收、传送。目前已能接收欧洲中期天气预报中心(ECMWF)、美国环境预报中心(NCEP)、加拿大气象中心(CMC)等国家的集合预报资料,预报时效达到10~16天。
在TIGGE全球集合预报资料中,我们可以提取各国数值预报中心集合预报初始扰动场信息,代表不同集合预报初值扰动方法的初值不确定性特征,为我们发展区域集合预报提供初值不确定性的来源。开展TIGGE集合预报资料的科学研究,为提升我国全球和区域集合预报技术发展和业务应用水平提供了一个非常好的契机。
在发展我国区域GRAPES模式集合预报方面,如何利用TIGGE全球集合预报资料,获得区域GRAPES集合预报的初值扰动场,这一问题值得研究。本文将基于TIGGE预报资料,研究利用TIGGE全球集合预报的大尺度不确定性信息,构造区域GRAPES集合预报的初值扰动方法和试验方案,并对2008年7月22日发生在黄淮地区的暴雨个例进行集合预报试验,分析由TIGGE资料驱动区域GRAPES模式的有效性。
1 “0 8.07.22 ”黄淮暴雨降水过程概况2008年7月22—23日,受高原低涡和西南暖湿气流共同影响,黄淮地区普降暴雨到大暴雨,湖北西部和北部、河南大部、山东南部、江苏北部、安徽北部等地24小时累计降水量一般在100~180 mm之间,局部地区降水量达200~240 mm(图 1a)。
|
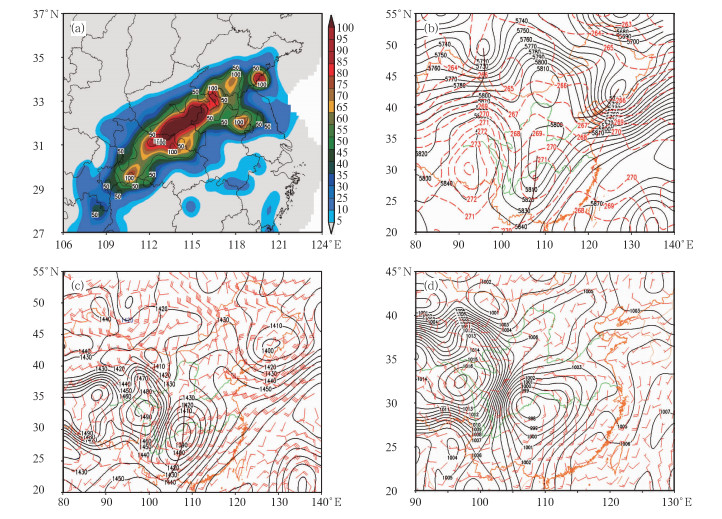
图 1 (a) 2008年7月22日00时至7月23日00时(世界时,下同)24小时累计降水量(单位:mm); (b) 2008年7月21日12时500 hPa高度场(实线, 单位:gpm)和温度场(虚线, 单位:K);(c) 2008年7月21日12时850 hPa高度场(单位:gpm)和风场(单位: m·s-1);(d) 2008年7月21日12时海平面气压场(单位: hPa)和地面风场(单位:m·s-1) Fig. 1 A heavy rainfall occurring in the Huanghuai area during 22-23 July 2008. (a) 24 h total precipitation from 00 UTC 22 to 00 UTC 23 July 2008 (unit: mm) and synoptic situation at 12 UTC 21 July 2008;(b) 500 hPa geopotential height field (unit:gpm) and temperature field (dashed line, unit:K); (c) 850 hPa geopotential height field (solid line, unit:gpm) and wind field (unit: m·s-1); (d) Sea level pressure (unit: hPa) and surface wind field (unit: m·s-1) |
21日12时,在500 hPa上(图 1b),欧亚中高纬地区为“两槽一脊”环流形势,低槽分别位于巴尔喀什湖附近和我国黑龙江以北地区,高压脊位于蒙古一带,并配合反气旋高压中心;西太平洋和南海上空为副热带高压控制,但强度较弱;在我国境内,甘肃南部有一低压中心,低压槽从甘肃伸展到四川和贵州一带,温度槽落后于低压槽,有冷平流配合。在850 hPa上(图 1c),重庆北部受西南低涡控制,低涡中心为低于1400 gpm的等高线,其东侧为强盛的西南暖湿气流,最大风速超过12 m·s-1,向暴雨中心输送了大量水汽,为暴雨产生提供了有利的水汽条件。在地面图上(图 1d),在30°N附近有纬向倒槽生成,倒槽内低压中心位于西南地区,中心气压值达998 hPa,低压中心位置与西南涡一致。同时,冷空气扩散南下进入河套地区,在河套西部地区形成锋生气旋,地面锋生明显。
从地面到高空形势可以看出,此次暴雨过程是在高空槽、西南低涡、切变线和地面倒槽的共同作用下发生的。
2 数值模式与TIGGE资料简介 2.1 GRAPES数值模式简介本文采用中国气象科学研究院数值预报研究中心等单位联合开发的GRAPES-MESO(Global/Regional Assimilation and Prediction System)区域模式3.0版本,时间积分方案为半隐式半拉格朗日方案,网格设计为等经-纬度格点,水平方向采取Arakawa-C格点,垂直方向采取Charney-Philips非均匀跳层分布,垂直高度坐标为地形追随坐标。模式物理过程包括云微物理显式降水、次网格积云对流参数化、长波辐射、短波辐射、陆面过程、近地面过程以及边界层过程。
试验中模式预报区域中心点取为(39.75°N、107.65°E),水平分辨率为0.15°×0.15°,水平格点数为502×330,垂直方向为33层,模式预报区域覆盖了上述暴雨区域。模式积分开始时间为2008年7月21日12时(世界时),时间步长为180秒,共积分72小时。模式背景场和侧边界条件来自国家气象中心全球中期预报模式T213分析场,利用常规探空资料对背景场进行同化和初始化,获得模式初值,模式侧边界条件每6小时更新一次。
2.2 TIGGE集合预报资料简介表 1是中国气象局(CMA)、欧洲中期天气预报中心(ECMWF)和美国环境预报中心(NCEP)3个TIGGE中心的集合预报资料概况。如表可见,每个中心的集合预报成员数目不同、分辨率不同、预报时效不同,如集合预报成员数目一列,CMA为15个,ECMWF为51个,NCEP为21个。但每个中心提供的要素是统一的,均提供8个等压面(100、250、300、500、700、850、925、1000 hPa)位势高度H,比湿Q,温度T,纬向风U,经向风V,320 K等位温面的位涡资料,等位涡面的位温资料,地表的28个要素资料。本文将采用CMA、ECMWF和NCEP 3个TIGGE中心的2008年7月21日12时(世界时)等压面集合预报资料,以下分别简称CMA-EPS,ECMWF-EPS,NCEP-EPS。
|
|
表 1 3个TIGGE中心集合预报资料概况 Table 1 The outline of ensemble forecast data from three TIGGE centers |
TIGGE资料是全球模式集合预报产品,可以反映大尺度系统预报的不确定性特征。本文将通过对TIGGE资料进行处理,产生反映大尺度系统预报不确定性特征的TIGGE扰动场,并通过一定的数学处理方法,在GRAPES模式初值场中加入TIGGE扰动场信息,形成区域GRAPES集合预报的初始扰动场。以下详细地介绍利用TIGGE资料产生GRAPES集合预报初始扰动场的数学处理方案:
第一步:利用双线性插值方案,将CMA、ECMWF、NCEP的TIGGE全球集合预报资料插值成0.15°×0.15°分辨率的数据。
第二步:挑选最具代表性的TIGGE集合预报成员。
TIGGE集合预报成员与相应的TIGGE控制预报在分析时刻的均方差越大,初值扰动场就越具有代表性,越能代表大尺度系统的初值不确定性特征。选取模式积分开始时间2008年7月21日12时(世界时)的500 hPa高度场,分别计算了各TIGGE中心集合预报成员与相应TIGGE控制预报在模拟区域内的均方差:
| $ \sigma {\rm{ = }}\sqrt {\frac{1}{{n}}\sum\limits_{i = 1}^n {{{\left( {X - Y} \right)}^2}} } $ |
式中X为TIGGE集合预报成员,Y为相应的TIGGE控制预报,n为模拟区域内的格点数。计算结果表明,CMA集合预报成员的均方差最大,NCEP次之,ECMWF最小,分别为11.0~17.0 gpm、9.0~15.0 gpm和2.6~4.3 gpm。Du等[9]等人的研究表明:用8~10个集合预报成员已经可以提高降水预报技巧,这一点对我们构建区域GRAPES集合预报系统是有意义的。因此,为减少计算资源,我们从3个TIGGE中心集合预报系统中各选取了5个均方差较大的集合预报成员,共产生15个集合预报成员(如表 2所示)。对ECMWF被选取的第36、42、16、26和4个集合预报成员,简称为ECMWF036,ECMWF042,ECMWF016,ECMWF026和ECMWF004。对CMA和NCEP被选取的集合预报成员,以此类推。例如:对CMA被选取的第9个集合预报成员,简称为CMA009,不再赘述。
|
|
表 2 经挑选的具有代表性的3个TIGGE中心集合预报成员 Table 2 The ensemble members chosen from three TIGGE centers |
第三步:计算大尺度初值扰动场dX(x,y,z)。
| $ {\rm{d}}X\left( {x, y, {z}} \right) = X\left( {x, y, z} \right) - {X_i}\left( {x, y, z} \right) $ |
式中X(x,y,z)为TIGGE中心集合预报成员的初值,Xi(x,y,z)为相应的TIGGE控制预报的初值。由上述计算公式可获得各TIGGE中心集合预报成员的纬向风U、经向风V、温度T、比湿Q以及位势高度H在8个等压面层(100、250、300、500、700、850、925、1000 hPa)上的尺度初值扰动场dX(x,y,z)。
第四步:将TIGGE高度场H扰动量转换为GRAPES模式扰动气压Pip的扰动量。
GRAPES模式的变量为纬向风U、经向风V、温度T、比湿Q以及扰动气压Pip,与TIGGE资料提供的物理量差异主要表现在,GRAPES模式是等高面的扰动气压Pip,而TIGGE资料提供的是等压面的高度场H。由GRAPES模式系统动力框架可知,扰动气压Pip与高度场H的关系为:
| $ \begin{array}{l} {P_{{\rm{ip}}}} = \frac{R}{{{c_{\rm{p}}}}}{\left( {{\rm{lev/1000}}{\rm{.0}}} \right)^{\frac{{R - {c_{\rm{p}}}}}{{{c_{\rm{p}}}}}}}\left( {1.0/100000.0} \right)\\ \;\;\;\;\;\;\;\; \times \left( { - gH} \right) \end{array} $ |
设扰动气压的扰动量为ΔPip:
| $ \begin{array}{l} \Delta {P_{{\rm{ip}}}} = \frac{R}{{{c_{\rm{p}}}}}{\left( {{\rm{lev/1000}}{\rm{.0}}} \right)^{\frac{{R - {c_{\rm{p}}}}}{{{c_{\rm{p}}}}}}}\left( {1.0/100000.0} \right)\\ \;\;\;\;\;\;\;\; \left( { - g} \right)\left( {H_{{\rm{lev}}}^{{\rm{cont}}} - H_{{\rm{lev}}}^{{\rm{perb}}}} \right) \end{array} $ |
式中cp为空气定压比热,R为干空气比气体常数,g为重力加速度,(
第五步:TIGGE大尺度扰动场dX(x,y,z)的垂直插值处理。
通过第三步获得了由TIGGE资料产生的大尺度初值扰动场dX。由于TIGGE的大尺度初值扰动场dX(x,y,z)是等压面资料,GRAPES模式是地形高度追随坐标,需要将TIGGE等压面上的扰动场转换为GRAPES模式面上的扰动场。GRAPES模式面有33层等高垂直坐标,但是TIGGE扰动场信息是8个等压面层(100、250、300、500、700、850、925、1000 hPa)上的数据。将8层TIGGE大尺度扰动场加入到GRAPES模式面33层的初值场中遵循表 3的对应关系。例如:对于GRAPES模式面的第1~5层(GRAPES模式面高度为0~500 m),采用1000 hPa的TIGGE扰动场资料,以此类推,不再赘述。
|
|
表 3 GRAPES模式面与TIGGE扰动场的对应关系 Table 3 The corresponding relation between GRAPES model levels and TIGGE perturbation fields |
第六步:产生GRAPES模式面的扰动初值场init′(x,y,z)。
| $ {\rm{init'}}\left( {x, y, z} \right) = {\rm{init}}\left( {x, y, z} \right) - {\rm{d}}X\left( {x, y, z} \right) $ |
其中init(x,y,z)为GRAPES控制预报模式面初值场,dX(x,y,z)为TIGGE大尺度初值扰动场。
4 区域GRAPES模式集合预报试验方案表 4是GRAPES模式集合预报试验方案。其中控制预报采用国家气象中心GRAPES-MESO业务模式系统,模式背景场和边界条件由国家气象中心的T213全球模式产生。按照第3部分介绍的扰动初值方案,从CMA-EPS,ECMWF-EPS,NCEP-EPS中分别产生5个扰动初值,总计获得15个扰动初值。扰动成员的边界条件与控制预报相同,未做扰动。为考虑云微物理过程与边界层过程的预报不确定性,采用了多物理过程组合方案,将3个云微物理参数化方案(Ncep-3class,Wsm-3scheme,Wsm-6scheme)与2个边界层过程参数化方案(YSU方案和MRF方案)进行随机组合,与上述15个扰动初值相对应,设计了15个区域GRAPES集合预报成员。对2008年7月22日发生在黄淮地区的一次暴雨过程进行了集合预报试验,对由TIGGE资料驱动的区域GRAPES集合预报的有效性进行了详细分析。
|
|
表 4 3个TIGGE中心不同集合预报成员所对应的物理过程组合方案 Table 4 The combination schemes of physical processes for different ensemble members chosen from three TIGGE centers |
选取TIGGE资料中ECMWF的集合预报成员,分析其200 hPa纬向风U、500 hPa扰动气压Pip、850 hPa温度T的初值扰动场的水平结构特征。图 2~图 4依次给出了ECMWF的3个集合预报成员200 hPa纬向风U、500 hPa扰动气压Pip、850 hPa温度T的初值扰动场。
|
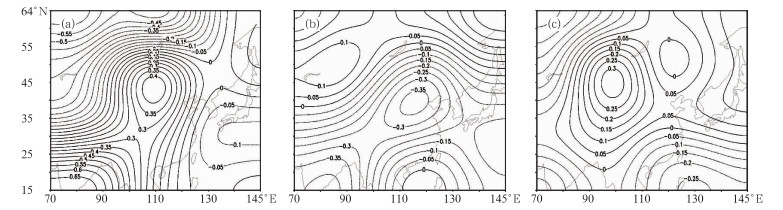
图 2 基于ECMWF中心集合预报成员产生的GRAPES模式200 hPa纬向风U的扰动值(单位:m·s-1) (a) ECMWF036;(b) ECMWF042;(c) ECMWF016 Fig. 2 The perturbation values (m·s-1) of initial zonal wind field on 200 hPa level for GRAPES ensemble members based on TIGGE-ECMWF initial perturbations (a) ECMWF036, (b) ECMWF042, (c) ECMWF016 |
|
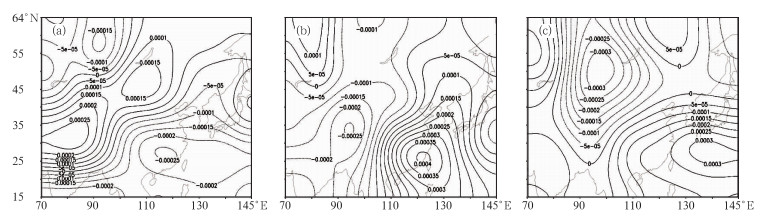
图 3 基于ECMWF中心集合预报成员产生的GRAPES模式500 hPa扰动气压Pip的扰动值ΔPip(单位:Pa) (a) ECMWF036;(b) ECMWF042;(c)ECMWF016 Fig. 3 The perturbation values ΔPip(Pa) of initial disturbed pressure Pip on 500 hPa level for GRAPES ensemble members based on TIGGE-ECMWF initial perturbations (a) ECMWF036, (b) ECMWF042, (c) ECMWF016 |
|
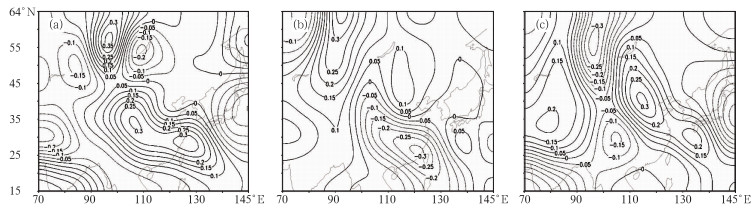
图 4 基于ECMWF中心集合预报成员产生的GRAPES模式850 hPa温度T的扰动值(单位:K) (a) ECMWF036;(b) ECMWF042;(c) ECMWF016 Fig. 4 The perturbation values of the initial temperature (K) on 850 hPa level for GRAPES ensemble members based on TIGGE-ECMWF initial perturbations chosen from the ECMWF center (a) ECMWF036, (b) ECMWF042, (c) ECMWF016 |
由200 hPa纬向风U的水平扰动结构(图 2)可以看出,集合预报成员ECMWF036在以(33°N、110°E)为中心的狭长区域内出现了一个较大的扰动值,最大扰动值达到了0.4 m·s-1,集合预报成员ECMWF042的扰动结构特征与集合预报成员ECMWF036相似,但一般呈现负的扰动结构,最大扰动值达到了-0.35 m·s-1;集合预报成员ECMWF016以30°N为分界线,呈现“南负北正”的扰动结构特征,在其以北地区出现正的扰动结构,最大扰动值达到了0.3 m·s-1,在其以南地区出现负的扰动结构,最大扰动值达到了-0.25 m·s-1。
从天气形势上看,在西南地区上空有一低涡存在,蒙古境内、甘肃南部分别存在一个高压中心和低压中心,西北太平洋由副热带高压控制,这些都是产生暴雨的重要天气系统。从500 hPa扰动气压Pip的水平扰动结构(图 3)可以看出,3个集合预报成员在这些区域的水平扰动结构各不相同,以110°E为分界线,集合预报成员ECMWF036的水平扰动呈现“西正东负”的结构特征,扰动中心值为-0.00025~0.00025 Pa,而集合预报成员ECMWF042则呈现“东正西负”的扰动结构特征,其扰动中心值为-0.00025~0.0004 Pa;集合预报成员ECMWF016以30°N为分界线,呈现“北正南负”的扰动结构特征,其扰动中心值为-0.0003~0.0003 Pa。
另外,我们还注意到:在西北太平洋上,3个集合预报成员的扰动强度均较大,集合预报成员ECMWF016与ECMWF036的最大扰动强度在0.0003~0.0004 Pa之间,集合预报成员ECMWF042的最大扰动强度在0.00025 Pa左右。这表明:所选的集合预报成员在较大程度上包含了对西北太平洋副热带高压预报不确定性的表达。
由850 hPa温度T的水平扰动结构(图 4)可以看出:以45°N为分界线,集合预报成员ECMWF036的水平扰动呈现“南正北负”的结构特征,而集合预报成员ECMWF042则呈现“南负北正”的扰动结构特征;集合预报成员ECMWF016的扰动结构呈现“正-负-正”的纬向变化特征。3个集合预报成员的扰动强度在-0.3~0.3 K之间。
初值扰动场较大的相似性将会限制集合预报成员间的离散度的增长,离散度偏小将导致集合预报成员漏报大气真实状态的概率增加。由初始时刻所获得的集合预报成员200 hPa纬向风U、500 hPa扰动气压Pip、850 hPa温度T的水平扰动结构可以看出:文中所构造的初值扰动场差异较大,可以使集合预报成员能够最大程度的表征初值场的不确定性,可以保证集合预报成员包含大气真实状态的概率增加,这对集合离散度的合理增长有正的影响。
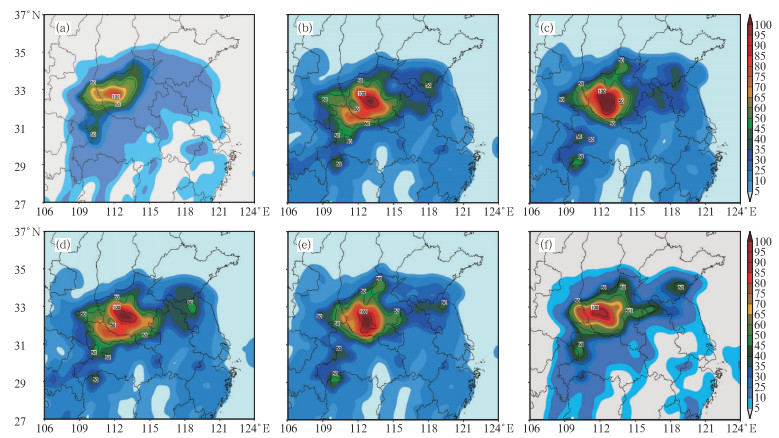
5.2 集合预报试验结果分析图 5给出了控制预报与ECMWF中心5个集合预报成员的24小时累积降水预报。与实况(图 1a)对比可以看到:控制预报(图 5a)的强降水范围明显偏小,暴雨中心降水值只有50 mm左右,而实况降水强度达到了100 mm以上。此外,控制预报漏报了山东南部、江苏北部和安徽北部地区的强降水中心。图 5b~5f是ECMWF中心5个集合预报成员预报的24小时累计降水量。由降水预报结果来看,与控制预报(图 5a)相比,集合预报对这次暴雨降水过程的总体预报效果是不错的,集合预报成员能很好地反映出降雨带的走向,都不同程度地对控制预报的暴雨中心降水强度及范围有一定的改善,暴雨中心的降水强度均在100 mm以上,某些集合预报成员的降水预报结果与实况非常接近(图 5b、图 5f)。尤其值得注意的是,各集合预报成员对山东南部、江苏北部和安徽北部地区的强降水表现出了一定的预报能力,给出了控制预报中没有反映出来的降水特点,这可以给预报员以很好的指示作用。
|
图 5 控制预报(a)与ECMWF中心集合预报成员(b~f)的24小时累计降水预报(单位:mm) Fig. 5 The 24 h total precipitation forecast of (a) control forecast and (b-f) ensemble members chosen from ECMWF center (unit: mm) |
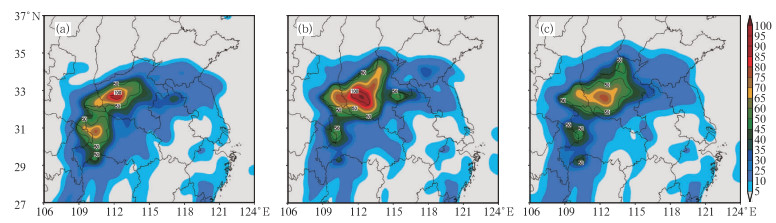
图 6、7分别给出了这次暴雨过程24小时累计降水集合预报平均和集合离散度。由图 6可以看出,各TIGGE中心的集合预报平均都模拟出了这次暴雨过程的西南-东北向降雨带,并在河南中部模拟出了一个暴雨中心,但各TIGGE中心模拟的暴雨中心降水值差别较大,ECMWF与CMA的集合平均值达到了100 mm以上,而NCEP的集合平均值只有50 mm左右。另外,各TIGGE中心的集合平均都在安徽北部模拟出了较强的降水中心,其中,ECMWF的集合平均还在山东南部模拟出了一个较强的降水中心。因此,可以看出,集合平均的降水预报效果更接近实况,表明集合预报结果优于单一控制预报。
|
图 6 3个TIGGE中心:(a) CMA,(b) ECMWF,(c) NCEP给出的24小时累计降水集合预报平均(单位:mm) Fig. 6 The ensemble mean of 24 h total precipitation for (a) CMA, (b) ECMWF, (c) NCEP (unit: mm) |
|
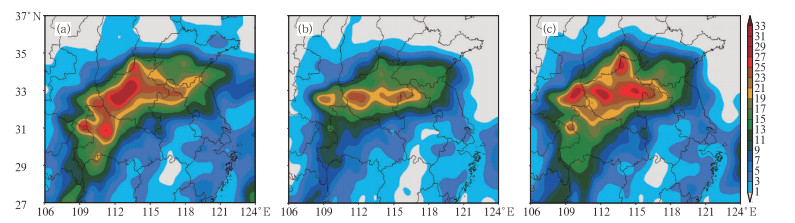
图 7 3个TIGGE中心:(a) CMA,(b) ECMWF,(c) NCEP给出的24小时累计降水集合离散度(单位:mm) Fig. 7 The ensemble spread of 24 h total precipitation for (a) CMA, (b) ECMWF, (c) NCEP (unit: mm) |
集合离散度是预报可信度的一个指标,定义离散度为集合扰动预报与集合平均预报之间的平均距离。集合离散度越大,表示预报不确定性越大。本次试验的集合离散度表明:在各TIGGE中心集合预报平均最大降水中心的区域,集合离散度也较大。CMA,ECMWF和NCEP的离散度值一般大于20 mm,表明集合扰动成员对这些区域暴雨降水量级的预报存在较大差别。
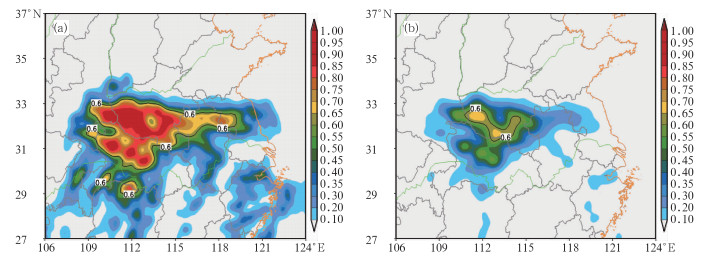
图 8给出了这次暴雨过程24小时累计降水大于25.0 mm和50.0 mm的概率预报。图中实线区域表示发生概率高于60%。由图 8b可以看到,在大于50.0 mm的降水概率预报图上,概率分布外形与降雨带相近,图中概率高于60%的区域与图 1a中实际发生暴雨的区域近于吻合。安徽与江苏北部地区出现暴雨的概率值大于0.4,表明以上地区出现暴雨的可能性较大,体现了概率预报对强降水预报具有相当高的可信度。由此可见,降水概率预报很好地指示了降水极值区域并给出了高值降水发生的概率,这些预报信息与控制预报是有差异的,如果在这次暴雨预报中参考集合预报结果,将对预报结果产生正面的影响效果。
|
图 8 3个TIGGE中心的24小时累计降水(a)大于25.0 mm与(b)大于50.0 mm的概率预报 Fig. 8 The probability forecast of 24 h total precipitation chosen from the three TIGGE centers (a) greater than 25.0 mm and (b) greater than 50.0 mm |
为定量分析集合预报系统的降水预报效果,计算了ECMWF集合预报成员、集合预报平均、控制预报的6小时预报的0.1 mm(小雨)、4.0 mm(中雨)和13.0 mm(大雨)降水的TS值和BS值(图 9)。

|
图 9 ECMWF中心5个集合预报成员、集合预报平均(ens mean)、控制预报(control)6小时分级降水TS评分(a,b,c)与BS评分(d,e,f)时间演变 (a),(d)大于0.1 mm;(b),(e)大于4.0 mm;(c),(f)大于13.0 mm Fig. 9 The time-evolution of TS and BS of 6 h precipitation (a, d) greater than 0.1 mm, (b, e) greater than 4.0 mm, (c, f) greater than 13.0 mm for ensemble members chosen from ECMWF center, ensemble mean (ens mean), and control forecast (control) |
由图 9可以看出:对于0.1 mm量级的降水,ECMWF集合预报成员的TS值达到0.2以上,集合预报平均的TS值达到了0.6以上;对于4.0 mm和13.0 mm量级的降水,ECMWF集合预报成员和集合预报平均的TS值较小,但集合预报平均的TS值仍然高于大部分集合预报成员的TS值。由BS值的时间演变可以看到:对于0.1 mm量级的降水,集合预报平均以及部分ECMWF集合预报成员的BS值大于1.0,说明对于小雨这一量级降水而言,初值扰动方法存在较大的空报;对于4.0 mm和13.0 mm这两个量级的降水,集合预报平均以及ECMWF集合预报成员的BS值均小于1.0,说明对于中雨和大雨这两个量级降水,初值扰动方法存在较大的漏报。由图 9还可以看出:对于以上3个量级的降水,在模式积分过程中,集合预报平均的TS值和BS值高于大部分ECMWF集合预报成员与控制预报。这说明:基于初值扰动方法的集合预报平均的预报结果总体上要优于集合预报的单个成员。
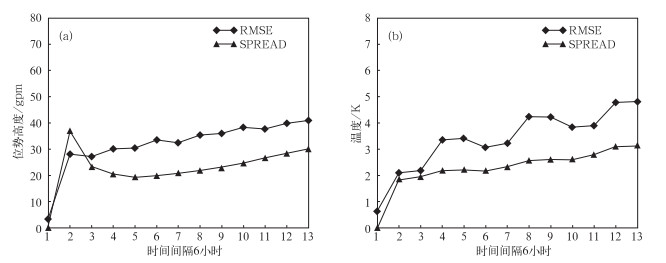
5.3 集合预报检验图 10给出了500 hPa位势高度与850 hPa温度集合离散度与集合平均预报均方根误差的时间演变。由图可以看出,在积分初期,集合离散度要大于或近似等于集合平均预报均方根误差,集合离散度基本满足要求,体现了文中基于TIGGE资料构造的区域GRAPES集合预报系统具有其合理性;随着模式积分时间向前推进,区域GRAPES集合预报系统虽然仍能保持一定的离散度,但集合平均预报均方根误差的增长速度更快,这可能是由于模式在积分过程中的动力调整作用,减小了初值扰动对预报结果的影响。可见,在更长预报时效上,本文由TIGGE资料驱动的区域GRAPES集合预报系统存在离散度增长速度偏慢的问题,集合离散度还有待于进一步改善。
|
图 10 500 hPa位势高度(a)与850 hPa温度(b)集合离散度与集合平均预报均方根误差的时间演变 Fig. 10 The time-evolution of ensemble spread (SPREAD) and root mean square error (RMSE) of(a) 500 hPa geopotential height and (b) 850 hPa temperature.(x-coordinate at intervals of 6 h) |
本文基于TIGGE资料,研究了区域GRAPES集合预报的初值扰动方法,并对2008年7月22日发生在黄淮流域的大暴雨过程进行了集合预报试验,检验了这种方法的合理性及有效性,得到以下主要结论:
(1) 基于TIGGE资料构造的初值扰动场差异较大,使得集合扰动成员能够最大限度地表征初值场的不确定性,这对集合离散度的合理增长有正的影响,保证了集合扰动成员包含大气真实状态的概率增加,提高了区域GRAPES集合预报系统捕获极端降水天气的能力。
(2) 在降水预报方面,相对于单一确定性预报,区域GRAPES集合预报系统对降水预报具有显著的改进作用。集合平均预报及降水概率预报均能够有效地给出控制预报中没有反映出来的中尺度降水特点,强降水发生概率较高的区域与实况对应关系较好,概率预报结果的可信度较高。
(3) 总体而言,集合离散度随时间增长。积分初期,暴雨的预报一致性(集合离散度)和预报技巧(集合平均预报均方根误差)之间的关系显示了本文基于TIGGE资料构造的区域GRAPES集合预报系统是合理的,但积分后期,由于模式在积分过程中的动力调整作用,减小了初值扰动对预报结果的影响,限制了集合离散度的增长速度。
本文只是针对一个暴雨个例展开讨论,对本次试验的分析和检验工作只是初步进行的,若将该方法应用于业务预报中还需要更多的研究和试验,有待今后进一步开展。
| [1] |
Toth Z. Meeting summary:Ensemble forecasting in WRF[J]. Bull Amer Meteor Soc, 2001, 82(4): 695-697. DOI:10.1175/1520-0477(2001)082<0695:MSEFIW>2.3.CO;2 |
| [2] |
陈静, 陈德辉, 颜宏. 集合数值预报发展与研究进展[J]. 应用气象学报, 2002, 13(4): 497-507. |
| [3] |
李俊, 纪飞, 齐琳琳, 等. 集合数值天气预报的研究进展[J]. 气象, 2004, 31(2): 3-7. DOI:10.7519/j.issn.1000-0526.2004.02.001 |
| [4] |
杜钧, 陈静. 单一值预报向概率预报转变的基础:谈谈集合预报及其带来的变革[J]. 气象, 2010, 36(11): 1-11. DOI:10.7519/j.issn.1000-0526.2010.11.001 |
| [5] |
刘家峻, 张立凤, 关吉平, 等. 集合预报产品在台风麦莎预报中的应用[J]. 气象, 2010, 36(5): 21-31. DOI:10.7519/j.issn.1000-0526.2010.05.003 |
| [6] |
陈德辉, 沈学顺. 新一代数值预报系统研究进展[J]. 应用气象学报, 2006, 17(6): 773-777. DOI:10.11898/1001-7313.20060614 |
| [7] |
李勇, 王雨. 2007年夏季GRAPES-MESO 15及30 km模式对比检验[J]. 气象, 2008, 34(10): 81-89. DOI:10.7519/j.issn.1000-0526.2008.10.011 |
| [8] |
徐双柱, 张兵, 谌伟. GRAPES模式长江流域天气预报的检验分析[J]. 气象, 2007, 33(11): 65-71. DOI:10.7519/j.issn.1000-0526.2007.11.010 |
| [9] |
谭燕, 陈德辉. 基于非静力模式物理扰动的中尺度集合预报试验[J]. 应用气象学报, 2007, 18(3): 398-407. |
| [10] |
Toth Z, Kalney E. Ensemble forecasting at NCEP and the breeding method[J]. Mon Wea Rev, 1997, 125(6): 3297-3319. |
| [11] |
Du J. Short-range ensemble forecasting of quantitative precipitation[J]. Mon Wea Rev, 1997, 125(10): 2427-2459. DOI:10.1175/1520-0493(1997)125<2427:SREFOQ>2.0.CO;2 |
 2011, Vol. 37
2011, Vol. 37 