2. 湖北省气象局气候变化中心, 武汉 430074
2. Climate Change Center of Hubei Meteorological Service, Wuhan 430074
随着我国气象探测自动化发展,许多人工观测的气象要素改为自动观测。在自动气象站中,采用铂电阻温度传感器测量空气温度,而采用湿敏电容湿度传感器测量空气相对湿度,然后根据相关公式计算其他湿度参量。显然自动气象观测站中没有湿球温度的观测,但湿球温度资料在工程设计、核电厂极端气象参数推求、制冷等方面有较为广泛的应用[1-4]。
由于湿球温度除了与湿度有关外,还与通风条件、湿球结冰、湿球温度表感应部分形状等有关。采用迭代等数值求解方法来推求湿球温度时大都忽略了这些问题,同时也未进行系统误差分析,使得这些方法在工程应用中不够严谨。为此本文分别采用逼近法和多元回归法,讨论湿球温度的估计过程,并基于全国134个基准气象站和湖北省75站的实测气象资料,对估计方法进行误差分析,同时分析不同通风条件及湿球结冰对湿球温度估计影响,为其在工程设计中应用提供一个较为全面的解决方案。
1 资料本文主要内容是利用气象要素估计湿球温度,对估计方法进行验证和评估的数据为全国134个基准气象站2001年24个时次、湖北省75个气象站1991—2000年10年的每天02、08、14、20时4个时次(一般气象站为后3个时次)的资料。气象要素包括逐时气压、气温(干球温度)、湿球温度、相对湿度、水汽压等资料,数据分别来源于国家气象信息中心资料室和湖北省气象档案馆,资料已经过有关质量控制方法检查[5]。
在我国气象部门的地面观测业务体制中,采用干湿温度表计算空气湿度的各个参量,不同时期不同台站有所差异。为减小因数据处理方法差异对湿球温度估计影响,本文剔除了差异较大的数据。具体方法是利用干湿温度表水汽压计算公式(即式(1))计算水汽压,如果所计算水汽压与台站提供的水汽压相差0.1 hPa以上,则剔除该时次数据。经统计被剔除的数据约占全部数据的1.6%。
2 湿球温度估计方法 2.1 逼近估计法在地面气象观测系统中,无论是自动观测还是人工观测,水汽压都是通过其他气象要素计算的物理量。为此本文以水汽压作为一个中间纽带,来推算湿球温度。按照地面气象观测规范[6],不同观测系统(主要指自动站和人工站),其水汽压计算公式不同。使用干湿温度表时,水汽压计算公式为:
| $ {{e}_1} = {f_1}\left( {t, {t_w}, p, A} \right) = {E_{{\rm{tw}}}} - {\rm{A}}p\left( {t-{t_w}} \right) $ | (1) |
式中, e1为水汽压(hPa),Etw为湿球温度tw所对应纯水平液面饱和水汽压(与tw有关),湿球结冰且湿球温度低于0 ℃时,为纯水平冰面饱和水汽压;A为干湿表系数,其值见表 2;p为本站气压(hPa);t为干球温度(℃);tw为湿球温度(℃)。
|
|
表 2 干湿表系数 Table 2 Psychrometer coefficients |
使用湿敏电容(自动观测站)直接测得相对湿度时,由相对湿度求水汽压公式为:
| $ {{e}_2} = {f_2}\left( {t, {u}} \right) = u{{\rm{E}}_{\rm{w}}} $ | (2) |
这样当e1=e2,就可求出湿球温度,即:
| $ {E_{{\rm{tw}}}} - {\rm{A}}p\left( {t- {t_w}} \right){\rm{ = }}u{{\rm{E}}_{\rm{w}}} $ | (3) |
式(2)、式(3) 中u为相对湿度(%);Ew为温度t所对应纯水平液面饱和水汽压(hPa)。式(1)~(3) 中,有关饱和水汽压计算,参见地面气象观测规范[6]。式(3) 中只有tw为未知变量,故可求出湿球温度。因Ew与tw函数关系较为复杂,所以无法利用式(3) 直接求解tw。为此本文采用逼近法求解tw。设:
| $ \begin{array}{l} \Delta {\rm{ = }}\min \left| {{e_1} - {e_2}} \right|\\ \;\; = \min \left| {{f_1}\left( {t, {t_w}, p, A} \right) - {f_2}\left( {t, {u}} \right)} \right| \end{array} $ | (4) |
选取合适的tw,采用逼近算法,使得式(4) 中的Δ最小,此时的湿球温度即为所求。
2.2 多元回归估计法采用逼近法求解湿球温度物理意义明确,精度也很高(后文将详细说明),但必须通过编写程序实现,使得该方法使用起来不够方便(特别是在工程设计中)。如在满足一定精度条件下,直接应用一个较为简便的经验公式或方程式来求解湿球温度,将会大大提高其在工程设计中的应用效率。因回归分析方法在气象业务与科研中有广泛应用[7-8],为此本文将气象站现有观测要素作为回归方程的因子,通过建立回归方程来估计湿球温度。经过因子筛选以及多次试验研究,因子采用本站气压、温度、水汽压、相对湿度4个要素较为合适。为减小误差,回归方程中加入了温度和水汽压的二次方因子。在进行误差分析时,发现误差与温度密切相关,即误差在不同温度范围差异较大,所以在建立回归模型时采用分段处理的方式进行。建立的回归方程见式(5)。
| $ {t_{\rm{w}}} = \left\{ \begin{array}{l} {a_1} + {b_1}p + {c_1}t + {d_1}{t^2} + {f_1}e + \\ \;\;\;\;{g_1}{e^2} + {h_1}u\;\;\;\;\;\;t \ge 22.0\\ {a_2} + {b_2}p + {c_2}t + {d_2}{t^2} + {f_2}e + \\ \;\;\;\;{g_2}{e^2} + {h_2}u\;\;\;\;\;\;22.0 > t \ge 6.0\\ {a_3} + {b_3}p + {c_3}t + {d_3}{t^2} + {f_3}e + \\ \;\;\;\;{g_3}{e^2} + {h_3}u\;\;\;\;\;\;6.0 > t \ge - 10.0 \end{array} \right. $ | (5) |
式(5) 中,p, t, e, u为本站气压、温度、水汽压、相对湿度,其单位和式(1)~(3) 相同。方程中ai, bi, ci, di, fi, gi, hi分别为回归系数,其中i取值1、2、3。
式(5) 中的回归系数采用最小二乘法求得,具体取值见表 1。为了使得回归方程具有时空代表性,本文进行了精心选样,并对回归模型进行了检验,结果表明回归效果非常显著(数据表略)。
|
|
表 1 式(5) 回归方程中的回归系数 Table 1 The regression coefficients in regression equation (5) |
为了评估逼近法和多元回归法估计湿球温度精度,本文首先利用全国134站2001年1—12月的逐小时实测资料,分别计算误差大小的频率分布特点,然后基于湖北地区10年的实测资料,对湿球温度的估计误差做进一步评估,从而为方法的应用者提供相关参考。为便于叙述,将估计值与实测值之差称为误差。
3.1 逼近法误差分析经统计,采用逼近法估计湿球温度时,平均误差为0.005 ℃,平均绝对误差0.02 ℃,误差的标准差0.02 ℃,最大绝对误差为0.19 ℃;出现误差为0.0 ℃的频次达98.8%,在±0.1 ℃以内的频次超过99.98%;极少部分误差绝对值超过0.1 ℃的数据出现在西北以及四川等地海拔高度大于2800 m的台站,在我国南方及中东部地区很少出现误差在±0.1 ℃范围以外的情况。
综上所述,采用逼近法推求湿球温度,估计值与实际观测值之间的误差很小,平均值不足0.01 ℃,估计值略高于观测值。结合误差出现的频次可以看出,采用逼近法来推算湿球温度,精度非常高,在很大程度上可取代人工实测湿球温度。
3.2 多元回归法误差分析在全国范围内,采用多元回归法估计湿球温度,逐小时误差在±0.2 ℃的频次为95.5%,而±0.4 ℃以内的频次超过了99%(见图 1a);最大绝对误差为1.5 ℃,出现误差较大的频次非常小,误差超过±0.8 ℃范围的频率不足0.12%。经统计,误差在0.8 ℃以上的情况都出现在海拔高度在2800 m以上的气象站,且集中在青海和四川2省。2800 m以下的气象站最大误差为0.78 ℃。全国134站有107站误差在±0.6 ℃范围以内。

|
图 1 误差频次分布及随各气象要素变化图(采用多元回归估计法) (a)误差频次;(b)误差随温度变化;(c)误差随水汽压变化;(d)误差随相对温度变化;(e)拟合误差与本站气压关系;(f)误差与随湿球温度变化 Fig. 1 The error frequency distributions versus meteorological elements when using the multiple regression estimation (a) error frequency distribution, (b) temperature, (c) vapor pressure, (d) relative humidity, (e) air pressure, and (f) wet-bulb temperature |
为分析多元回归法计算湿球温度误差与各相关气象要素的关系,本文制作了误差与温度、水汽压、相对湿度、本站气压、湿球温度等要素的散点图,见图 1b至图 1f。图中数据为全国134站2001年1—12月每月15日02、08、14、20时的资料。由图可知:(1) 绝大部分误差在±0.2 ℃以内;(2) 误差较大(误差绝对值大于0.4 ℃)主要集中在水汽压小于12 hPa、相对湿度小于45%、湿球温度小于12 ℃、本站气压小于780 hPa的范围内。由于本站气压主要反映了台站海拔高度,所以误差较大情况一般出现在海拔较高(大于2800 m)的台站。
3.3 湖北地区湿球温度估计误差分析上两小节湿球温度推算误差分析基于的是我国134个基准站资料,本节基于湖北省1991—2000年75站每日4次(一般气象站为3次)的资料,进一步讨论湿球温度估计误差分布情况。经统计,采用逼近法推算湿球温度时,在湖北省地区10年间只有8个时次的误差达到超过0.2 ℃,其中最大绝对误差为0.24 ℃;采用回归方法估计湿球温度的最大绝对误差为0.79 ℃,误差绝对值大于0.5 ℃总计350时次,占总次数的0.04%。由此可见,湖北地区湿球温度估计误差大小与全国基本一致。
下面以湿球温度的频率分析为例,评估不同估计方法的误差对于湿球温度频率计算的影响。在许多工程设计规程中,要统计最近连续不少于5年最炎热期3个月频率为10%的湿球温度。本文利用湖北省1991—2000年10年中6、7、8月的资料,分别采用两种估计方法推算的湿球温度,计算频率为10%的湿球温度,并与实测的频率为10%湿球温度进行比较。经计算,湖北75站中,采用多元回归法估计的频率为10%湿球温度与实测值差值最大(绝对值,下同)为0.19 ℃(出现在利川站,该站为湖北75站中海拔高度最高的气象站),其中最大差值小于0.1 ℃有59站, 占总站数的79%。采用逼近法计算的湿球温度频率与实测值最大差值为0.07 ℃,基本上与实测值的频率计算无差异。由此可见,采用上述两种估计方法推算的湿球温度,对于湿球温度的频率分析影响很小。
4 通风条件与湿球结冰对湿球温度估计影响 4.1 不同通风条件下估计湿球温度的差异在采用干湿温度表测量湿度时,不同通风条件及湿球温度表的感应部分形状,其干湿表系数不同[6],列于表 2。因干湿表系数的差异,导致水汽压不同,从而影响湿球温度的估计。前文逼近法和多元回归法推算的湿球温度都是基于现用百叶箱球状干湿表(通风速度0.8 m·s-1, 为叙述简便起见,将该通风条件简称现用通风条件)。为评估不同通风条件对湿球温度估计的影响,采用逼近法,利用表 2中3种干湿表系数,在其他气象要素相同情况下,推算不同通风条件下的湿球温度,并分别计算与现用通风条件下的差值(以下简称差值)。差值的平均值见表 3,表中数据表明,3种通风条件计算的湿球温度都高于现用通风条件。
|
|
表 3 不同通风条件与现用通风条件湿球温度的平均差值 Table 3 The mean difference of wet-bulb temperature between current ventilation condition and others |
通过分析,差值的变化幅度较大,且差值大小与相对湿度密切相关,见图 2。同时差值在温度大于等于0.0 ℃和小于0.0 ℃表现有所差异,造成这种差异的原因显然与其干湿表系数与湿球结冰与否不同有关。表 4给出了差值与相对湿度的关系式,其中y为差值(℃),u为相对湿度(%)。

|
图 2 不同通风条件与现用通风条件湿球温度差值随相对湿度变化图 Fig. 2 The variation diagram of wet-bulb temperature difference between current ventilation condition and others with relative humidity |
|
|
表 4 差值与相对湿度的关系式 Table 4 The relation between the difference and relative humidity |
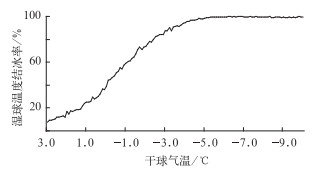
在地面气象要素采用人工方式观测时,湿球温度表结冰状态是通过实际观测而得。如采用自动方式测量空气湿度,就无法确定湿球温度表是否结冰。为此本文在估算湿球温度时,当温度大于等于0 ℃时,按湿球温度表未结冰处理,而低于0 ℃时,均按湿球结冰计算。这样处理简单实用,但与实际情况有所差异,因为在温度大于0 ℃时,湿球有可能结冰,而在温度在0 ℃以下,也会出现湿球不结冰的情况,这样必须评估采用该种方式处理时对湿球温度估计的影响。为此首先要了解在不同干球温度下,湿球结冰状况。本文统计了不同温度下湿球结冰百分率,见图 3。从图 3中可看出,在干球温度为3 ℃时,就有少数湿球结冰情况出现,在干球温度低于-0.4 ℃时,结冰率在50%以上,在干球温度为低于-3.3 ℃时,结冰率超过90%,以上结论的分析数据来自全国134站2001年资料。
|
图 3 湿球温度表结冰百分率 Fig. 3 The freezing percentage of wet-bulb thermometer |
挑选全国134站2001年气温在3 ℃至-10 ℃范围且湿球结冰的资料进行湿球温度估计。当温度大于等于0 ℃时,按湿球温度表未结冰处理,而低于0 ℃时,按湿球结冰计算,同时采用逼近法估计湿球温度,并将其与实测湿球温度进行比较分析,有如下结论:(1) 总体来说,会导致所推算的湿球温度比实测偏高,高出部分平均0.11 ℃,最多为0.29 ℃, 也有少部分偏低,但偏低出现频次仅为6.6%;(2) 估计值高出实测值0.20 ℃以上的时次占全部总时次的百分率不足4%。所以湿球结冰对湿球温度估计的影响不大。
5 讨论与小结本文设计了逼近和多元回归法两种方法估计湿球温度,应用人员可根据实际需求,选择其中一种方法,解决无湿球温度观测资料问题。采用逼近法只需本站气压、温度和相对湿度3个气象要素(尽管在前文推导过程中,使用了水汽压要素,但水汽压可通过温度和相对湿度计算)。逼近法估计湿球温度精度高,误差小,在全国范围内使用,效果很好。采用多元回归法估计湿球温度虽没有逼近法精度高,但总体误差可控制在一定范围内,且误差较大的频次非常小,因其使用简便,在工程设计中具有较广阔应用前景。如需要估计在不同通风条件下的湿球温度,可采用表 4中的回归方程进行订正。最后小结如下:
(1) 利用干湿球温度表计算水汽压公式,基于本站气压、温度和相对湿度3个气象要素,采用逼近法求解湿球温度精度很高,与实测值差值在±0.1 ℃以内的频率占99.98%,极端最大绝对差值不足0.19 ℃。
(2) 基于温度、相对湿度、水汽压、本站气压等4个要素因子,建立多元回归方程估计湿球温度,逐小时误差在±0.4 ℃范围以内的频次超过了99%;最大绝对误差为1.5 ℃,但出现误差较大的频次非常小,误差超过±0.8 ℃的频率不足0.12%,其中海拔高度低于2800 m的台站最大绝对误差为0.8 ℃。
(3) 不同通风条件对湿球温度估计的影响较大,其影响与相对湿度密切相关。随着相对湿度的增加,影响逐渐减小。
(4) 湿球结冰对湿球温度的估计影响不大。
需要说明的是本文对于湿球温度的推算及误差分析,有一个前提条件,即温度在-10 ℃以上。其原因是在该温度以下,一般不观测湿球温度。
| [1] |
袁业畅, 陈正洪. 大畈核电站拟址空气湿球温度推算[J]. 气象, 2008, 34(11): 69-73. DOI:10.7519/j.issn.1000-0526.2008.11.010 |
| [2] |
任遵海, 季玲, 董士冲, 等. 夏季湿球温度客观预报服务系统[J]. 气象, 1996, 21(5): 22-24. |
| [3] |
张磊, 孟庆林, 赵立华, 等. 湿热地区城市热环境评价指标的简化计算方法[J]. 华南理工大学学报(自然科学版), 2008, 36(11): 96-100. DOI:10.3321/j.issn:1000-565X.2008.11.018 |
| [4] |
张建一, 毛有花. 湿球温度变化与两级制冷装置的性能研究[J]. 制冷, 2002(2): 15-18. |
| [5] |
王新华, 罗四维, 刘小宁, 等. 国家级地面自动站A文件质量控制方法及软件开发[J]. 气象, 2006, 32(3): 107-112. DOI:10.7519/j.issn.1000-0526.2006.03.017 |
| [6] |
中国气象局. 地面气象观测规范[M]. 北京: 气象出版社, 2003.
|
| [7] |
魏瑞江, 王春乙, 范增禄. 石家庄地区日光温室冬季小气候特征及其与大气候的关系[J]. 气象, 2010, 36(1): 97-103. DOI:10.7519/j.issn.1000-0526.2010.01.015 |
| [8] |
张霞, 王新敏, 王全周, 等. 郑州雷电发生的环境场特征及潜势预报[J]. 气象, 2010, 36(6): 95-100. DOI:10.7519/j.issn.1000-0526.2010.06.015 |
 2011, Vol. 37
2011, Vol. 37 