2. 成都信息工程学院, 成都 610225;
3. 四川省气象台,成都 610071
2. Chengdu University of Information Technology, Chengdu 610225;
3. Sichuan Provincial Meteorological Observatory, Chengdu 610071
自动雨量站资料向来都是能够准确反映实时降雨量的主要依据,然而我国自动雨量站布设密度目前尚无具体标准,对已设置的数以万计的雨量站的合理性也未见有人进行过科学的论证,很多自动雨量站经历几次迁移后,地理位置信息已经不准确。另外,雨量的测量受风场影响很大,特别是翻斗式雨量计在大雨时, 由于翻斗翻动的惯性, 致使另一翻斗盛满水时还来不及翻转, 造成雨量流失, 使得测定的雨量有较大的误差, 记录失真,以及翻斗上的沾水或泥沙的影响都会阻碍翻斗的翻动,都有可能造成雨量的误差[1]。因此自动雨量站的质量控制问题已经越来越引起有关部门的重视。
近年来,国内在2004年出台了由气象台站,到省级、国家级资料部门的地面自动站观测资料三级质量控制(QC)业务系统(简称“三级质量控制系统”)[2],其中各级质量控制方法仍以传统方法为主,如:格式检查—极值检查—内部一致性检查—时间一致性检查—空间一致性检查—人机交互检查[3]。国外,尤其北欧各国在气象资料的质量控制规范化和技术上都处于世界先进行列,所用的空间质量控制方法主要有:Madsen-Allerup方法(丹麦)、DECWIM方法(挪威)、数值预报模式(HIRLAM)插值方法(挪威)、Kriging统计差值模式(芬兰)、MESAN方法(瑞典)等[4]。但自然降雨具有时空分布不均匀、降水面积和强度变化大的特点,常规的质量控制方法并不能很好地对其进行判别[5]。而雷达能实时探测云和降水结构及系统发生、发展演变情况,能迅速提供一定区域的实时降水情况。雷达站测的数据空间分布合理的优点,已经被广泛地应用于科研及业务应用各领域。因此本文在常规质量控制方法的基础上,引入雷达资料,研究一套结合雷达资料的自动雨量站资料质量控制的新方法。
1 所用资料及技术路线 1.1 资料雷达资料是2008年6月6—7日,广东省6部SA波段多普勒天气雷达(广州、深圳、梅州、韶关、阳江、汕头)1次/6 min的原始体扫资料,及对应时间广东省境内891个自动雨量站的6分钟降水资料(2008年6月6日00:00—6月7日23:54共480个)。
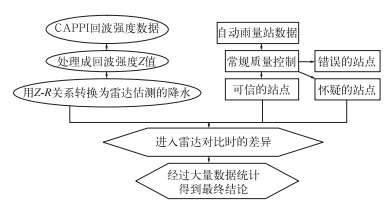
1.2 技术路线雷达和自动雨量站资料综合分析方法:首先,对自动雨量站资料进行常规质量控制,如地理位置信息检查—时间缺测检查—极值检查—时间一致连续性检查—空间一致性检查。通过常规质量控制后得到三类自动雨量站信息:怀疑的站点(A类)、可信的站点(B类)、错误的站点(C类)。C类站点可直接排除,A、B类站点的雨量资料和对应的雷达资料通过Z-R关系换算的估测雨量相对比,以计算相似离度的方式进行大量的数据分析,得出最终结论。其目的是通过层层质量控制找到确实存在问题的自动雨量站,为雷达估测降水提供可靠准确的自动雨量站数据。图 1为主要的技术流程图。
|
图 1 主要技术流程 Fig. 1 The main technical flow chart |
利用中国气象科学研究院灾害天气国家重点实验室开发的三维雷达组网软件[6],首先将各个单站的体扫资料数据采用NVI方法[7]插值到三维格点上,形成单站的三维格点数据,再把各单站的三维格点数据进行三维组网处理,得到各个格点的回波强度。在夏季0℃层亮带一般出现在3~5 km高度(有时会超过5 km),为了避免0℃层的影响,选取的CAPPI高度最好不要超过3 km。另外,离雷达越近,雷达估测降水就越可靠。综合考虑,故选取了3 km高度CAPPI的回波强度数据。
在降水估测时,Z-R关系(Z=aRb)的选取也极其重要。Z-R关系式为:
| $ Z=a{{R}^{b}} $ | (1) |
式(1) 中参数a和b的值与地区及降水的类型有关,在较大范围内变动[8]。目前常用的典型关系式为Z=200R1.6,但这种理论关系只适用于平均情况,因为一般某一次的降水实际上是不均匀的,且随时间变化,雨滴谱也随时间、空间和不同降水类型而变。从该次过程的回波强度及分布图(图略)上来看,以及自动站的雨强,我们判断该次过程属混合型降水,故取a=311, b=1.71。用式(2) 将回波强度的值Z1转换为式(1) 中的基本反射率因子Z,最后再用式(1) 反推雷达估测的降水R。
| $ Z={{10}^{{{Z}_{1}}/10}} $ | (2) |
自动雨量站数据是以时刻为文件名存放数据的,即每个时刻文件里存放所有自动雨量站的雨量数据,然而在经过地理位置信息检查后发现在不同的时刻中同一站点的经纬度信息却不尽相同,在被考察的891个自动雨量站中就有26个站点存在这样的问题。虽然这些站点的经纬度都在广东省境内,但不同的时刻却出现经纬度不一致的现象,导致其记录的雨量数据反映不出真实的信息,因此将这些站点列为错误的站点。
3.2 时间缺测检查理论上,以时刻为文件名的自动雨量站数据,在每一时刻存放的应该是所有自动雨量站此时段的降雨量,但事实上,每一时刻存放的自动雨量站个数却不同,显然这是某些时刻某些站点存在缺测的现象。在被考察的891个自动雨量站中有173个站存在不同时间的缺测现象。因此缺测时刻的雨量资料将不列入被考察的对象。
3.3 极值检查在进行了地理位置信息检查和时间缺测的检查后,得到865个站点无缺测时刻的6分钟降雨量。以每个站点为例,将各个站点全时段无缺测时刻的降雨量以站点名命名写成文件,对这865个站各自全时段无缺测时刻的降雨量进行极值检查。
首先,以一个站点为例,将该站点全时段无缺测时刻的降雨量按降序排列,取该站点全时段有降雨量的时刻点个数的1%的那个降雨量作为该站点的降雨量极值,因为在概率论中,我们把概率很接近于0(即在大量重复试验中出现的频率非常低)的事件称为小概率事件。一般多采用0.01即事件发生的概率在0.01以下的事件称为小概率事件,这个值常称为小概率标准。然后,取865个站点各自的降雨量极值的最大值(25.2 mm/6 min)作为本项极值检查的最终极值,这样可确保每个站点凡是大于此极值的概率都小于0.01,满足小概率事件的条件。
经过极值检查后,共有两个站没有通过此项检查。但并不能只因为没有通过极值检查就判定这两个站为错误的站点,暂且把它们列入怀疑的站点做进一步检验。
3.4 时间一致连续性检查降雨量随时间变化具有一定的规律,即相邻时间的降雨量应该有一定的变化范围。在被考察的865个站点无缺测的相邻时间的降雨量数据也应该符合此规律。
同样,首先将数据以站点号命名,每个文件记录该站点全时段无时间缺测的降雨量。以某一个站点为例,将每两个相邻时刻的降雨量差值按降序排列,取全时段有降雨量时刻点个数的1%(小概率事件理论)的那个降雨量差值,作为该站点时间一致连续性检查的阈值。然后,将所有的站按照此种方法计算阈值,最终取865个站点时间一致连续性检查阈值的最大值(6.7 mm/6 min即相邻两个6分钟的降雨量变化为6.7 mm)作为该项检查的阈值。
经过时间一致连续性检查,共有98个站点没有通过此项检查。把这些站点列入怀疑的站点做进一步检验。
3.5 空间一致性检查(Madsen-Allerupt方法)Madsen-Allerupt方法是Madsen等和Allerupt等发展的一种空间质量控制方法[9-12]。基本原理是基于某一空间范围内要素的空间分布是均一的假设。以某一台站i为例,记录下其周围N个邻近台站同时刻的观测值,将这些观测值按照从小到大的顺序排列,取这些观测值的中值和75%、25%分位值,计算统计量。公式如下
| $ {{T}_{it}}=({{X}_{it}}-{{M}_{t}})/({{q}_{t, 75}}-{{q}_{t, 25}}) $ | (3) |
| $ t={{q}_{t, 75}}-{{q}_{t, 25}} $ | (4) |
| $ S={{X}_{it}}/\sum\limits_{N=1}^{12}{{{x}_{itN}}} $ | (5) |
(当|Tit| > 2.00及Xit > 4时, 或当t=0(周围台站降水均很小),若S > 0.6及Xit > 4时, 则认为降水记录有误)。式中,Xit是t时刻台站i的观测值,Mt是N个邻近站t时刻观测值的中间值, qt, 75和qt, 25分别是N个邻近站t时刻观测值的75%和25%分位值。N的推荐值是12。
经过空间一致性检查,共有372个站没有通过此项检查,暂且把这些站点列入怀疑的站点做进一步检验。
在经过上述第3.1节、第3.2节、第3.3节、第3.4节、第3.5节检查后,除在地理位置信息检查中的26个站点可以确定为错误站点外,其余各项检查出的站点都不能只因为不符合某一项检查就断定该站点数据为错误,所以将没有通过各项检查的各个站点汇总,全部列为怀疑的站点(374个),记为A类,剩余的其他通过各项检查的站点(491个)全部列为可信的站点,记为B类。
4 雷达资料在自动雨量站资料质量控制中的应用在进行了上述常规质量控制后,本文将引入雷达资料,通过分析雷达反演的雨量和地面实测雨量的关系来对自动雨量站资料做进一步的质量控制。
4.1 相似离度的引入本文采用的数据是48小时内每6分钟一次(共计480个时刻)的雷达资料和自动雨量站资料。而传统上,常用的相似比较标准主要有相似系数、海明距离、欧式距离等,但除了海明距离尚能准确地比较出两样本的值相似程度(不能比较出形相似情况)之外,相似系数和欧氏距离都不理想。本文引用一种新的衡量相似程度的统计量——相似离度[13],即相似性的差异程度,既考虑到雷达反演雨量和地面实测雨量的形相似情况,又体现了它们的值相似差异,是一个比较全面的相似标准。
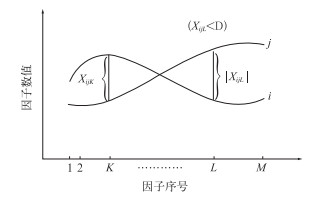
相似离度可以较客观地比较样本之间的相似性,用符号Cij表示i,j两个样本的相似离度。图 2(样本曲线图)中绘出i,j两条样本曲线。Cij可表示为:
| $ {{C}_{ij}}=\frac{1}{2}({{S}_{ij}}+{{D}_{ij}}) $ | (6) |
|
图 2 样本曲线图 Fig. 2 Sample graph |
其中:
| $ ~{{S}_{ij}}=\frac{1}{M}\sum\limits_{K=1}^{M}{\left| {{x}_{ijK}}-{{E}_{ij}} \right|} $ | (7) |
| $ {{D}_{ij}}=\frac{1}{M}\sum\limits_{K=1}^{M}{\left| {{x}_{ijK}} \right|} $ | (8) |
| $ {{x}_{ijK}}={{x}_{iK}}-{{x}_{jK}} $ | (9) |
| $ {{E}_{ij}}=\frac{1}{M}\sum\limits_{K=1}^{M}{{{x}_{ijK}}} $ | (10) |
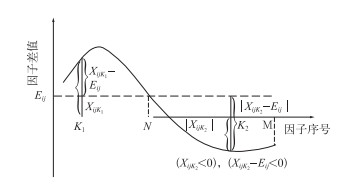
在此,Eij表示i样本对j样本中所有因子之间的总平均差值(见图 3)。
|
图 3 样本所有因子之间的总平均差值 Fig. 3 The overall average difference for all sample factors |
Dij实际上就是海明距离(一种用来表示两样本相似程度的参量)对因子容量M求平均值。它能准确地反映出两样本之间在总平均数值上的差异程度,在此称为值系数。
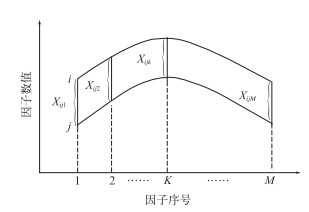
Sij能反映出两个样本中的各个因子之间的差值xijK对Eij的离散程度(参见图 3),显然,当两根样本曲线的形状将完全相似(如图 4)时,则xij1=xij2=, …, =xijM=Eij,Sij=0。相反,若各个xijK对于Eij的离散程度越大,则两根样本曲线的形状就越不相似。由此可知,Sij能较好地反映两样本间的形相似程度,称之为形系数。
|
图 4 完全相似的两根样本曲线图 Fig. 4 Two completely similar sample curves |
综上所述,相似离度由形系数Sij和值系数Dij两项共同决定。当两根样本曲线相重合时,由式(9) 知,xijK=0(K=1,2,…,M),所以由式(10) 得Eij=0,从而由式(7)、(8) 和(6) 可得Sij=0,Dij=0,Cij=0,三者都达到最小值0,相似离度也为0,这是最理想的相似情况。对一般的情况,从图 3可见,在K=K1处,|xijK1-Eij|比|xijK1|小一个|Eij|值,但在K=K2处,|xijK2-Eij|却比|xijK2|大一个|Eij|值,所以Sij与Dij的数量级相同,因此,本文的Cij值只由两者取简单平均求得。
4.2 相似离度的应用由第4.1节的讨论可知,相似离度可以较好地比较两样本的形相似和值相近情况,因此在利用雷达资料对自动雨量站数据进行质量控制中引入相似离度来进行分析比较。
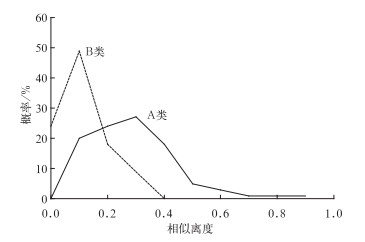
在第3节中,经过常规质量控制后得到两类自动雨量站数据(A类和B类),将这两类自动雨量站所有站点的实测雨量和雷达估测雨量分别做相似离度的计算,得到各个站点的相似离度,范围为(0~0.91641)。根据概率统计方法,将相似离度在[0, 0.05) 范围内的记为0,[0.05, 0.15) 内记为0.1,[0.15,0.25) 内记为0.2,[0.25,0.35) 内记为0.3,以此类推,至[0.95,1) 内记为1,得到表 1(A类),表 2(B类)及概率统计图 5。
|
|
表 1 A类(怀疑的站点)相似离度百分比 Table 1 Percentage of type-A (suspected site) analogy deviation |
|
|
表 2 B类(可信的站点)相似离度百分比 Table 2 Percentage of type-B (trusted site) analogy deviation |
|
图 5 相似离度概率分布图 Fig. 5 Probability distribution from the degree of similarity |
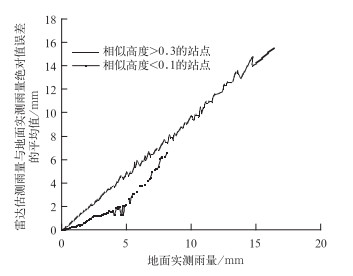
由第4.1节知,相似离度值越小则说明两条样本曲线的相似程度越高,反之亦然。在将雷达资料运用与自动雨量站质量控制中时,相似离度是重要的评判标准。由图 5显而易见,A类(怀疑的站点)相似离度的峰值为0.3,B类(不怀疑的站点)相似离度的峰值为0.1。据此可将所有站点以0.3和0.1作为划分依据,得到相似离度小于0.1的站点共计293个,相似离度大于0.3的站点共计158个,将两类站点分别进行误差统计分析,即:将全时段480个时刻的实测雨量和雷达估测雨量取差值的绝对值,以具有相同实测降雨量为准,将其对应的雷达估测雨量与实测雨量的绝对值求平均值,得到各个实测雨量与雷达估测雨量绝对值误差的平均值。将相似离度大于0.3的和相似离度小于0.1的所有站点都进行如此处理,最终得到雷达估测雨量与地面实测雨量绝对值误差分析图,如图 6。
|
图 6 雷达估测雨量与地面实测雨量绝对值误差分析图 Fig. 6 Radar estimates of rainfall and ground truth rainfall in the absolute value of error analysis diagram |
从图 6中可明显地看出,随着降雨量的增大,雷达估测的误差也在增大,但相似离度小于0.1的站点误差始终小于相似离度大于0.3的站点。由此可证实上述判断:相似离度大于0.3的站点确实存在问题。
5 分析不同类型雨量站资料情况及其与雷达资料的对比(1) 各类自动雨量站存在缺测时段的个数统计(如表 3)
|
|
表 3 各类自动雨量站存在缺测时段的个数统计 Table 3 The missing statistics for various types of automatic raingauge measurement periods |
缺测现象是自动雨量站数据记录中不可避免的情况,但它也可间接地反映出自动雨量站的稳定性和准确性。从表 3中可看出,错误站点中存在缺测站点的百分比是最高的,次之为怀疑的站点,最低的为可信的站点,这便很好地检验了常规质量控制方法的准确性。
(2) 各类自动雨量站资料和雷达资料的对比情况
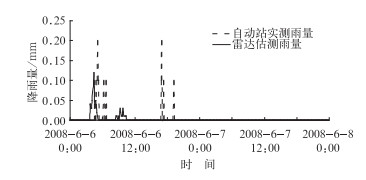
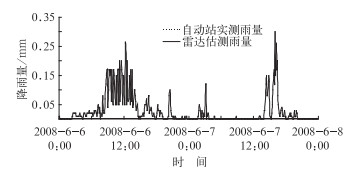
经过分析汇总后,错误的站点实测雨量和雷达估测雨量的相关趋势图主要有两种情况,一种为实测雨量和估测雨量的相关性差,如图 7为自动雨量站751560在480个时刻实测雨量和雷达估测雨量的相关趋势图,从图中可明显地看出二者是相错的;另外一种情况为实测雨量和估测雨量的有无不一致,如图 8为自动雨量站200076在480个时刻实测雨量和雷达估测雨量的相关趋势图,从图中可看出整个时段自动站实测雨量均为0而雷达估测的雨量却几乎覆盖这个时段。这两种情况都可证明错误的站点在地理位置信息上存在明显的问题,站点信息应该予以修正。
|
图 7 自动雨量站751560在480个时刻实测雨量和雷达估测雨量的相关趋势图 Fig. 7 Correlation trends between the rainfall measured by automatic rainfall station 751560 in 480 times and that by radar rainfall estimates |
|
图 8 自动雨量站200076在480个时刻实测雨量和雷达估测雨量的相关趋势图 Fig. 8 As in Fig. 7 but for station 200076 |
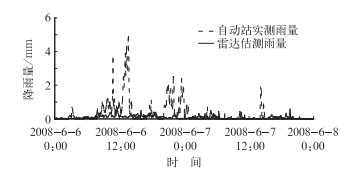
图 9为相似离大于0.3的自动雨量站200079在480个时刻实测雨量和雷达估测雨量的相关趋势图。
|
图 9 自动雨量站200079在480个时刻实测雨量和雷达估测雨量的相关趋势图 Fig. 9 As in Fig. 7, but for station 200079 |
从图 9中可直观地看出,此站的实测雨量和雷达估测雨量的相关性较差,没有明显的趋势一致性,且峰值和低谷基本没有吻合。
图 10为相似离度小于0.1的自动雨量站758033在480个时刻实测雨量和雷达估测雨量的相关趋势图。

|
图 10 自动雨量站758033在480个时刻实测雨量和雷达估测雨量的相关趋势图 Fig. 10 As in Fig. 7, but for station 758033 |
从图 10中可以直观地看出,此站的实测雨量和雷达估测雨量的相关性较好,趋势基本一致,峰值和低谷均比较吻合。
6 其他个例分析根据2008年夏季华南地区的降雨情况,本文又选取了2008年6月24日00:00—15:54时(160个时次)以及25日00:00—23:54时(240个时次)两次个例进行上述的常规质量控制和相似离度分类。
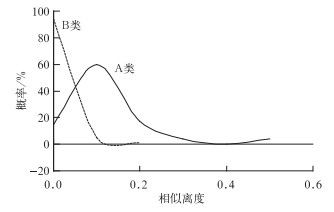
其中24日个例中,在经过地理位置信息检查后,共有16个站点没有通过此项检查,剩下的875个站点中有57个站点没有通过常规质量控制的,余下818个站点通过了各项常规质量控制。按照上述个例分析的相似离度统计,得到A类可疑站点相似离度概率峰值为60%,对应的相似离度为0.1,B类可信站点相似离度概率峰值为94%,对应的相似离度为0,如表 4、表 5及图 11。
|
|
表 4 2008年6月24日A类(可疑站点)相似离度百分比 Table 4 Percentage of type-A (suspected site) analogy deviation for the 24 June 2008 case |
|
|
表 5 2008年6月24日B类(可信站点)相似离度百分比 Table 5 Percentage of type-B (suspected site) analogy deviation for the 24 June 2008 case |
|
图 11 2008年6月24日相似离度概率分布图 Fig. 11 Probability distribution from the degree of similarity correspond to the 24 June 2008 case |
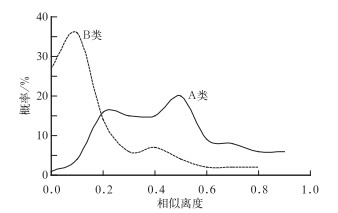
其中25日个例中,在经过地理位置信息检查后,共有18个站点没有通过此项检查,剩下的873个站点中有375个站点没有通过常规质量控制的,余下498个站点通过了各项常规质量控制。按照上述个例分析的相似离度统计,得到A类可疑站点相似离度概率峰值为20%,对应的相似离度为0.5,B类可信站点相似离度概率峰值为36%,对应的相似离度为0.1,如表 6、表 7及图 12。
|
|
表 6 2008年6月25日A类(可疑站点)相似离度百分比 Table 6 Percentage of type-A (suspected site) analogy deviation for the 25 June 2008 case |
|
|
表 7 2008年6月25日B类(可信站点)相似离度百分比 Table 7 Percentage of type-B (suspected site) analogy deviation for the 25 June 2008 case |
|
图 12 2008年6月25日相似离度概率分布图 Fig. 12 As in Fig. 11, but for the 25 June 2008 case |
其他各类分析在此不一一列举。
7 结论(1) 3个个例在进行地理位置信息检查后分别有26、16、18个站点没有通过此项检查。求其并集最终得到26个站点是错误的站点,这也能够说明第一个个例具有的代表性、全面性。
(2) 6、7日个例中根据常规质量控制和相似离度的分析后,可疑的站点与可信站点相似离度的峰值分别为0.3和0.1,24日个例中分别为0.1和0,25日个例中分别为0.5和0.1。24日个例中两类相似离度峰值的划分显然不够有说服性,究其原因主要为24日的降水与6、7日以及25日比较而言,降雨强度小时间短且范围不广,这也是此方法的局限性。因此在选取个例中应尽量选取降雨强度大时间长且覆盖范围广的个例。另外就单个个例而言,各类相似离度的峰值也不是固定不变的,应具体情况具体分析。
(3) 根据结论(1)、(2) 的阐述,应重点分析6、7日个例和25日个例,其中6、7日个例中相似离度大于0.3的可疑站点共计144个,25日个例中相似离度大于0.5的可疑站点共计146个。其中有30个站点同时出现在这两类中,可将其列为有严重问题的站点,其余230个站点可列为有一般问题的站点。
综上所述,本文在利用多个个例分析后,最终得到,在被考察的891个自动雨量站资料中,约有2.9%(26个)自动雨量站资料可确定为错误的,约有3.4%(30个)自动雨量站资料被列为有严重问题,约有25.8%(230) 个自动雨量站资料被列为有一般问题,需向有关部门反映,以便及时查找问题,为雷达定量估测降水提供准确的自动雨量站数据。
| [1] |
黄玲. 自动气象站雨量误差分析及维护[J]. 气象与减灾研究, 2006, 29(2): 64. |
| [2] |
任芝花, 熊安元. 地面自动站观测资料三级质量控制业务系统的研制[J]. 气象, 2007, 33(1): 20-22. |
| [3] |
王新华, 罗四维, 刘小宁, 等. 气象国家级地面自动站A文件质量控制方法及软件开发[J]. 气象, 2006, 32(3): 108-112. |
| [4] |
熊安元. 北欧气象观测资料的质量控制[J]. 气象科技, 2003, 31(5): 316-317. |
| [5] |
张强, 涂满红, 马舒庆, 等. 自动雨量站降雨资料质量评估方法研究[J]. 应用气象学报, 2007, 18(3): 365-367. |
| [6] |
张志强, 刘黎平, 谢明元, 等. CINRAD三维组网拼图产品显示系统[J]. 气象, 2007, 33(9): 19-24. DOI:10.7519/j.issn.1000-0526.2007.09.003 |
| [7] |
肖艳娇, 刘黎平. 新一代天气雷达网资料的三维格点化及拼图方法研究[J]. 气象学报, 2006, 64(5): 647-656. DOI:10.11676/qxxb2006.063 |
| [8] |
刘娟, 宋子忠, 刘东风, 等. 分级Z-I关系及其在淮河流域雷达测雨中应用[J]. 气象科学, 1999(2): 213-220. |
| [9] |
Rissanen P, Jacobsson C, Madsen H, et al. Nordic methods for quality control of climate data[J]. DNMI-Report 2000, No.10/2000 KLIMA
|
| [10] |
Vejen F, Jacobsson C, Fredriksson U, et al. Quality control of meteorological observations automatic methods used in the Nordic countries[J]. Climate Report, 2002, No. 8/ 2002, KLIMA http://docplayer.net/25766606-Quality-control-of-meteorological-observations.html
|
| [11] |
Eischeid J K, Baker C B, Karl T R. The quality control of longterm climatological data using objective data analysis[J]. J Appl Meteor, 1995, 34: 2787-2795. DOI:10.1175/1520-0450(1995)034<2787:TQCOLT>2.0.CO;2 |
| [12] |
Rudel E. Report and Review about Data Processing and Quality Control Procedures Involved in the Conversion of Manually Operated Station to Automatically Operated Station[R]. World Climate Programme: Data and Monitoring No. 31, WMO2TD No. 833, 1997. http://smallbusiness.chron.com/quality-assurance-process-procedures-4809.html
|
| [13] |
李开乐. 相似离度及其使用技术[J]. 气象, 1986, 44(2): 174-177. DOI:10.11676/qxxb1986.024 |
 2011, Vol. 37
2011, Vol. 37 