2. 宿迁市气象台,宿迁 223800;
3. 江苏省气象台,南京 210008
2. Suqian Meteorological Office of Jiangsu Province, Suqian 223800;
3. Jiangsu Meteorological Observatory, Nanjing 210008
空气负离子(negative air ion, NAI)主要是由空气中含氧负离子与若干个水分子结合而形成的原子团,被统称负氧离子。负氧离子浓度是环境空气质量监测、评价的重要指标。进入21世纪以来,随着社会对气候变化、气象环境的关注,研究人员对负氧离子展开了广泛的研究与应用,并获得了一些新的成果。就气象环境与负氧离子浓度关系的而言,已有研究表明空气负离子浓度可能与多种气象要素相关[1-9]。例如,有研究表明空气湿度对空气负离子浓度影响最大,其次是光照强度,最小是温度[1-2];但也有研究认为空气负离子浓度与相对湿度、风速、云量、日照、降水量的相关性不显著[3-3]。有研究认为影响空气负离子浓度的气象因子有日平均风速、太阳辐射、相对湿度等,空气负离子浓度与日平均风速、太阳辐射正相关,与相对湿度负相关[4-4];有的研究却认为空气负离子浓度与温度、2分钟风速等呈负相关,与湿度在春、夏、冬三季正相关(在秋季负相关)[5-6]。显然,基于常规线性回归分析方法的气象环境与负氧离子浓度关系的研究,存在着许多不确定性,甚至矛盾性的结论。
值得一提的是,相关研究结论的不确定性给相关业务预报、科研工作带来了困扰。为了更客观、更准确地揭示气象因子对大气负离子浓度的影响程度,本文拟根据森林区和城市区空气负离子实测资料,选取尽可能多的气象要素资料,采取通径分析(Path Analysis)方法,研究气象因子对空气负离子浓度的贡献,以期获得对空气负离子浓度影响因子的准确认识,从而为空气负离子浓度预报提供参考,并为不同地理位置的空气负离子研究提供参考。
1 资料和方法 1.1 资料来源本文空气负离子资料来源于两个具有代表性地貌的负离子观测站,分别位于宿迁市气象局观测站(城市区)和嶂山森林公园(森林区)。观测仪器采用北京WIMD-A系列大气负离子自动测报仪,其符合国家推荐标准《空气离子测量仪通用规范》,采集精度高,能实现从数据采集到传输的全部自动化、智能化。经过中国气象局大气探测中心以及江苏省、贵州、河北等地的使用,表明其防御各种恶劣天气和技术性故障的性能突出,其自动测报部分性能稳定,工作可靠[10]。负离子一般用迁移率来表示其大小,负离子越大,迁移率就越小。对人体有益的中小负离子,迁移率一般大于0.06。本研究试验观测仪器每次测量自动检测3种迁移率(0.15、0.40、1.00) 的负离子浓度值,每天记录24组负离子值。
观测对应的气象要素资料,采集同期逐日平均气压、平均气温、平均水汽压、相对湿度、蒸发量、总云量、10分钟平均风速和日照百分率。同时还收集同期逐日雨(雪)量,用作晴雨天气条件分型之用,本研究中定义当日无降水发生,即雨(雪)量小于0.0 mm时为“无雨日”,其余为“雨日”。
本研究资料观测时间为2005年8月1日至2006年8月31日。
1.2 通径分析方法统计学理论在研究多个相关变量间的线性关系时,一般采用简单相关分析或多元回归分析方法,多元回归与简单相关分析相比,在一定程度更真实表现各自变量与因变量的关系,此种方法在气象统计研究上已有成熟的研究应用[11-13]。但是在多元回归分析中,偏回归系数带有单位,因而不能直接比较各自变量对因变量的效应。通径分析方法克服上述不足,因而在农业、环境等领域得到较多应用[14-20]。一般认为该方法在研究多个相关变量间的关系时具有精确、直观等优点,使用通径系数(path coefficient)可以不受度量单位和自变量变异程度的影响去评估自变量对因变量的效应(相对重要性),也能区分自变量对因变量的直接作用和间接作用[21]。而且该方法中以通径系数的大小表示各因子相对于结果的相对重要性,较大的剩余通径系数表示因子对结果误差较大,或者还有其他的更重要的因素需要被考虑[22-23]。可见,采用通径系数的通径分析方法,可获得比相关分析和回归分析更为准确的结论,特别适合本文的研究目的。其基本模型[24]如下。
设在k个自变量x1,x2,…,xk中,每两个变量之间与因变量y之间的简单相关系数可以构成求解通径系数的标准化正规方程:
| $ \left\{\begin{aligned} {r_{11}}{p_{1y}} + {r_{12}}{p_{2y}} +, \cdots, + {r_{1k}}{p_{ky}} = {r_{1y}}\\ {r_{21}}{p_{1y}} + {r_{22}}{p_{2y}} +, \cdots, + {r_{2k}}{p_{ky}} = {r_{2y}}\\ \vdots \\ {r_{k1}}{p_{1y}} + {r_{k2}}{p_{2y}} +, \cdots, + {r_{kk}}{p_{ky}} = {r_{ky}} \end{aligned}\right. $ | (1) |
式中,rij为变量xi与xj的简单相关系数,riy为自变量xi与因变量y的简单相关,p1y,p2y,…,pky为直接通径系数,即自变量xi与因变量y标准化后的偏相关系数,表示xi对y的直接影响效应,rijpjy为间接通径系数,表示xi通过xj对因变量y的间接影响效应。通径系数可以使用多元回归分析理论中F检验或t检验进行显著性分析,其方法在统计书籍中均有详细描述,本文不再赘述。
目前对影响空气负离子浓度的气象、环境因子认识尚在探索之中,已有研究模型采用的自变量因子不尽相同,存在遗漏重要因子的可能性,因此本研究在通径系数基础上,进一步采用“决定系数”评估各自变量对因变量的相对决定程度。定义:
| $ \begin{array}{l} {R_i} = p_{iy}^2\\ {R_{ij}} = 2{P_{iy}}{r_{ij}}{p_{jy}}\\ {R_e} = 1 - {R_i} - \sum\limits_{i \ne j} {{R_{ij}}} \end{array} $ | (2) |
式中, Ri为自变量xi对因变量y的直接决定系数,Rij为xi通过xj对因变量y的间接决定系数,Re为其他因子作用的剩余决定系数。若Re很大,说明分析中可能遗漏了某些主要影响因素。应说明的是,决定系数不能进行统计检验,只能进行大致的判断[12]。
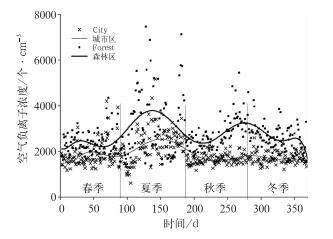
2 结果分析 2.1 城市和森林区的空气负离子浓度分布就全年而言,森林区具有比城市区更多的空气负氧离子浓度(图 1),特别是夏季(6—8月)、秋季(9—11月)森林区的空气负离子浓度是城市的2~3倍,表明森林区的空气比城市要好,此结论与现有研究[3, 5]的结论是一致的。对于森林区,空气负离子的浓度均大于城市,这种差异与下垫面植被茂盛有关。夏季森林区植被茂盛,释放的负离子要比城市大得多,也是一年中森林区、城市区负离子浓度差别最大的季节;秋季虽然绿色植被比夏季少,但城市空气干燥、浮尘多,负离子存活时间较森林短,因而城市区负离子浓度总体上仍低于森林区。到了冬、春季,森林区植被覆盖相对夏、秋季减少,负离子浓度较少,并与城市的负离子浓度的差值进一步减小。
|
图 1 观测期城市区和森林区空气负氧离子浓度逐日变化 Fig. 1 Daily changes of negative air ion concentration during the one-year observation period in urban (marked by ×) and forest (marked by ·) zones |
如前所述,气象因子对负离子的浓度是有影响的,过去由于资料长度、计算分析条件限制,对这种影响程度如何、何种气象要素对负离子的贡献最大等问题存在争议。过去研究一般考虑气温、湿度、风速、日照等4~5个气象因子[1, 9],为了获得更全面、客观的结论,本文选取了8个逐日基本气象要素如逐日平均气压(X1)、气温(X2)、水汽压(X3)、相对湿度(X4)、蒸发量(X5)、总云量(X6)、日平均风速(X7)、日照百分率(X8)和城市、森林区负离子浓度,采用通径分析方法,分别就无雨日、雨(雪)日各气象要素对空气负离子浓度的关系作进一步研究。
不同于常见的统计相关检验,这里我们利用文献[24]提供的方法,计算给出p值代表的准确性显著性水平,以便检验在给定的p值水平上是否接受原假设。只有当p值小于0.05时(表 1中无划横线的数值),回归模型在统计学上才有意义。各气象要素与负离子迁移率的相关分析结果如表 1所示,可见城市中,总云量(X6)、平均风速(X7)和日照百分率(X8)与空气负离子浓度相关不显著;蒸发量(X5)与空气负离子浓度在无雨日显著相关(通过0.05显著性水平检验),而在雨日则不显著相关。
|
|
表 1 城市区日平均气象因子与空气负离子浓度的相关系数和通径系数 Table 1 Correlation and path coefficients between meteorological factors and NAI concentration in urban zone |
同样的,对森林区的分析发现(表 2),总云量(X6)、平均风速(X7)、日照百分率(X8)与森林区的空气负离子浓度也是不显著相关。与城市区不同的是,森林区空气负离子浓度还与蒸发量(X5)不显著相关。此外,平均相对湿度(X4)与空气负离子浓度的相关关系在不同的天气条件也不尽相同,在雨日两者相关不显著(未通过0.05显著性水平检验),但是在无雨日相关显著。
|
|
表 2 森林区日平均气象因子与空气负离子浓度的相关系数和通径系数 Table 2 Correlation and path coefficients between meteorological factors and NAI concentration in forest zone |
相关分析结果可见在雨日或无雨日天气条件下,无论是城市区还是森林区,总云量、平均风速、日照百分率与空气负离子浓度不显著相关。城市区的日平均蒸发量、森林区的日平均相对湿度,在无雨日和雨日对空气负离子浓度具有不同的相关关系。特别的,与空气负离子浓度显著相关的气象要素中,各相关系数在森林区基本一致,而在城市区差异明显,与日平均水汽压(X3)和日平均气温(X2)有关的相关系数较其他相关系数要高。
2.3 气象要素对空气负离子浓度的通径分析 2.3.1 直接通径效应分析应用通径分析方法分析城市、森林区空气负离子迁移率与各气象要素的真实关系,结果亦列于表 1和表 2中。
城市区中,各气象因子对空气负离子浓度直接影响效果作用较大(即通径决定系数较大)的两个因子依次为:(1) 平均水汽压(X3)>(2) 平均气温(X2),第一因子平均水汽压的直接决定系数达到平均气温的直接决定系数的1.97倍(无雨日达到2.63倍)。明显的,第一因子平均水汽压和第二因子平均气温对空气负离子浓度的影响,要远远大于相对湿度等其他因子的影响。注意到这两个主要的影响因子中,平均水汽压的直接通径系数为正,表明平均水汽压(X3)对空气负离子浓度产生最大的直接效应,亦即空气负离子浓度主要受水汽压的影响。由于水汽压同时又是空气温度的函数,进一步表明另外一个主要因子即平均气温是空气负离子浓度的决定性因子。这与文献[2]的结论一致。
表 2也表明,森林区中,日平均水汽压(X3)也是对空气负离子浓度影响最大的因子,但与城市区有差别的是,影响空气负离子浓度的第二、第三因子随天气状况(雨日、无雨日)不同而有所区别:无雨日除第一因子之外的其他因子间的差异不明显,而雨日第一因子不变,日平均气温(X2)明显大于剩余的因子,为第二因子,且在雨日对空气负离子浓度有负的通径效应,在无雨日有正的通径效应。这是因为森林区植被覆盖面积大,林区湿度变化幅度小,树木的遮蔽作用又使得林区气温少变,在雨日气温降低,水汽压减小,抑制空气负离子的释放,而在无雨日气温升高,水汽压增大,反而有利于负氧离子的释放。
计算各个气象要素的直接决定系数,可见8个气象因子中,以日平均水汽压(X3)最为重要,日平均气温(X2)次之。综合各因素分析还发现,平均气温(X2)和相对湿度(X4)对空气负离子浓度的直接通径系数与相应的相关系数异号,可见气温和湿度虽然与空气负离子浓度具有正相关的关系,但最终的影响效果却是负的。
研究对森林区四季气象因子对负离子的作用也作了通径分析(表 3)。结果表明,四季中对空气负离子直接作用最大的气象因子不尽相同,夏季直接作用最大的是平均水汽压,而在冬、春、秋季最大的因子是平均气温,且平均气温在这三季中的直接效应也有明显差别,如秋季的平均气温对空气负离子浓度是负的通径效应。
|
|
表 3 森林区四季气象因子直接作用通径系数 Table 3 Direct path coefficients of meteorological factors to the NAI concentration in the four seasons of forest zone |
分析还发现,虽然平均相对湿度、平均气温对空气负离子浓度的直接通径系数较大,但相应的相关系数在各天气(无雨、有雨)、各季节中或大或小,亦即单个气象要素的简单改变对空气负离子浓度的影响较小,还应深入的分析各天气因子影响空气负离子浓度的间接通径系数,即一种气象因子通过哪些其他因子对负离子浓度产生影响,及其影响的大小。
2.3.2 间接通径效应分析分析各气象因子对空气负离子浓度的间接作用能力(表略),平均气压(X1)、平均气温(X2)、相对湿度(X4)、蒸发量(X5)通过水汽压(X3) 对负离子浓度的间接通径效应强烈,除了平均气压(通过水汽压)对空气负离子浓度有较强的负效应外(雨日达到-1.065,无雨日达到-0.873),平均气温、相对湿度等(通过平均水汽压)对空气负离子浓度有明显的正效应。
进一步比较选定的气象因子在各区晴雨日对负离子浓度的产生的间接通径效应大小,城市区只有两个因子,最大为平均水汽压(共占13/16),其次为平均气温(共占3/16);森林区有4个因子,依次为平均水汽压(共占12/16)、平均气温(共占2/16)、平均相对湿度和平均气压(各占2/16)。可见,平均水汽压是城市区和森林区中最大的间接效应因子,它与平均气温、平均气压、平均相对湿度,形成了对空气负离子浓度间接影响最大的气象因子结合。
值得注意的,对剩余通径系数的计算表明,城市区和森林区中,气象要素对空气负离子浓度作用的剩余通径系数较大(大于0.80)。较大的剩余通径系数,表明气象类因子对空气负离子浓度变化直接、间接作用较小,大气环境中还存在其他重要的环境因子影响空气负离子浓度变化。
3 结论本研究主要揭示影响空气负离子浓度变化的主要环境因子,借以提高城市、森林等常见下垫面类型的空气负离子浓度业务预报和环境评价能力。在选取了尽可能多的气象因子,并辅以在揭示因子贡献分析上较为先进的通径分析方法,分析了城市环境和森林环境下大气负氧离子浓度的差异,并对气象因子与空气负离子浓度的关系作了探讨,获得了气温、湿度、气压等8类气象因子对大气负离子浓度的相对重要性,得到如下的结论。
(1) 相同天气条件下,森林区和城市区负氧离子浓度变化不同。森林区大气负氧离子浓度要比城市高,夏、秋季节森林区的空气负离子浓度达到城市区的2~3倍,森林区的空气更有益于人体健康。
(2) 相关分析表明,总云量、平均风速和日照百分率同城市和森林空气负离子浓度相关不显著。蒸发量与森林区空气负离子浓度相关不显著,且仅在无雨日与城市区空气负离子浓度显著相关。
(3) 对气象要素与负离子浓度的通径分析表明,日平均水汽压、日平均气温是影响城市区和森林区空气负离子浓度的主要直接因子。日平均水汽压还是其他气象要素影响空气负离子浓度的主要间接因子。
(4) 城市区和森林区气象要素对负离子浓度的剩余通径系数达到0.8以上,较大的剩余通径系数表明还有其他重要的因素影响大气负离子浓度变化。
由于空气负离子产生机制和影响因子的复杂性,空气负离子浓度变化研究一直是气象、环境、林业等多学科交叉课题,空气负离子浓度变化的环境影响评价结论,既与研究区域地理位置、下垫面的差异有关,又与大气环境中气象要素间的相互作用有关。值得说明的是,已有的研究表明空气负离子浓度可能与多种气象要素相关,但在具体因子的分析上,结果仍存在不确定性,一方面与统计分析方法本身的约束条件有关,另一方面与大气环境中气象要素间的相互作用的复杂性、研究区域地理位置、气候背景、下垫面的差异性有关。本文结果基于对江苏省宿迁市城区和森林区两个观测站点一年的观测资料,表明空气负离子浓度变化存在其他重要的影响因子,但由于站点少、观测时间短,研究结果难免存在一定的局限性,如何探明这些其他重要因素及其与负离子浓度的关系,这需要在今后的观测试验中,增加有关要素观测,并做进一步研究。
韦朝领, 王敬涛, 蒋跃林, 等, 2006. 合肥市不同生态功能区空气负离子浓度分布特征及其与气象因子的关系[J]. 应用生态学报, 17(11): 2158-2162. DOI:10.3321/j.issn:1001-9332.2006.11.032 |
王继梅, 冀志江, 隋同波, 等, 2004. 空气负离子与温湿度的关系[J]. 环境科学研究, 17(2): 68-70. |
唐春燕, 蔡哲, 肖安, 等, 2011. 井冈山空气负离子浓度特征及其与气象条件关系[J]. 安徽农业科学, 39(1): 495-496. |
叶彩华, 王晓云, 郭文利, 2000. 空气中负离子浓度与气象条件关系初探[J]. 气象科技, 28(4): 51-52. |
丛菁, 孙立娟, 2010. 大连市负氧离子浓度分布及预测模型的建立[J]. 气象与环境学报, 26(4): 44-47. |
李伟, 王柏林, 李书严. 空气负离子日变化规律以及与主要气象要素相关性分析. 中国气象学会2007年年会气象综合探测技术分会场论文集[C]. 广州, 中国气象学会, 2007: 173-183.
|
周晓香, 洪辉, 王钰, 2007. 资溪县城空气负离子特征及与气象因子相关性分析[J]. 气象与环境学报, 23(6): 32-34. |
王淑娟, 王芳, 郭俊刚, 等, 2008. 森林空气负离子及其主要影响因子的研究进展[J]. 内蒙古农业大学学报(自然科学版), 29(1): 243-247. |
孟丽红, 张敏, 姚青, 2011. 2009年天津城区空气负离子变化规律[J]. 气象与环境学报, 27(1): 27-29. |
李伟, 王经业, 陆勇, 等, 2008. 大气负离子自动测报仪的研制[J]. 气象科技, 36(6): 834-836. |
王海军, 2011. 两种湿球温度估计方法比较及误差分析[J]. 气象, 37(4): 497-502. DOI:10.7519/j.issn.1000-0526.2011.04.015 |
李蕊, 牛生杰, 汪玲玲, 等, 2011. 三种下垫面温度对比观测及结冰气象条件分析[J]. 气象, 37(3): 325-333. DOI:10.7519/j.issn.1000-0526.2011.03.010 |
段旭, 丁圣, 许美玲, 2010. 预报因子选取及方程建立人机交互平台[J]. 气象, 36(11): 120-125. DOI:10.7519/j.issn.1000-0526.2010.11.019 |
张淑杰, 张玉书, 吴微微, 等, 2009. 辽宁省玉米螟发生程度的气象预报模型[J]. 中国农业气象, 30(2): 262-266. |
程海涛, 慕彩芸, 2009. 东疆地区蒸发量变化趋势及气象影响因子研究[J]. 气象, 35(7): 68-72. DOI:10.7519/j.issn.1000-0526.2009.07.010 |
袁志发, 周静芋, 郭满才, 等, 2001. 决策系数——通径分析中的决策指标[J]. 西北农林科技大学(自然科学版), 29(5): 131-133. |
武新民, 2004. 气象因素与疟疾的数学模型研究进展[J]. 中国公共卫生, 20(7): 877-878. DOI:10.11847/zgggws2004-20-07-76 |
陈观浩, 1999. 气象因子对稻瘿蚊发生程度的通径分析[J]. 广西植保, 12(3): 4-6. |
宋世德, 周静芋, 袁志发, 等, 1998. 通用选择指数的通径分析话模型[J]. 生物数学学报, 13(3): 300-305. |
张存良, 殷毓芬, 吴祥云, 1994. 通径分析的系统理论及分析[J]. 农业系统科学与综合研究, 10(1): 41-47. |
崔党群, 1994. 通径分析的矩阵算法[J]. 生物数学学报, 9(1): 71-76. |
敬艳辉, 邢留伟, 2006. 通径分析及其应用[J]. 统计教育, (2): 24-26. |
姜丽, 2001. 通径系数分析法运用初探[J]. 统计与决策, (12): 12-13. DOI:10.3969/j.issn.1002-6487.2001.12.001 |
唐启义, 2010. DPS数据处理系统[M]. 北京: 中国科技出版社, 655-662.
|
 2012, Vol. 38
2012, Vol. 38 