2. 新疆巴州气象局,库尔勒 841000
2. Meteorological Office of Bayinggolin Mongolia Autonomous Prefecture, Korla 841000
所谓“百里风区”是指兰新铁路在新疆境内从了墩车站到大步车站约100 km铁路的沿线范围。在这个区段≥8级的大风日数平均每年约100天;其中十三间房车站一带平均每年大风日数多达140天。每年春、夏季是大风最盛行的时期。近年来实测最大瞬时风速曾经达60 m·s-1以上。
新疆铁路风灾表现形式主要有大风吹翻列车、积沙埋道、击碎车窗玻璃、铁路行车设施损毁、道床板结、车辆溜逸、钢轨磨损增大、大风停轮等。兰新线(途径百里风区)自开通运营以来,遭遇过多次大风灾害。据统计,新疆境内铁路运输因风害造成列车脱轨、倾覆事故为32起,损毁货车111节,客车11节。因大风造成的列车停轮更是数不胜数,严重影响了运输效益,也造成了不良的社会影响。百里风区和天山有着很直接的关系,天山横亘新疆,每当冷空气来的时候,天山山脉会挡住冷空气的去路,但是在天山东部却有一段小的缺口,就是色皮山口,位于东天山山脉的博格达山与巴里坤山脉之间,冷空气可从此缺口处翻越天山,一泻千里。百里风区的天山山脉段,其北坡较平缓,坡度约为0.009,山口中山脊的最高处海拔高度约为1700 m,与上游来风方向的准噶尔盆地南沿的高差约为700 m。这样的坡度和高差极易强冷空气翻越。按照杨国祥等[1]提出的冷空气翻山的判别式为Q<F/N,U>NH[其中Q为坡度,F为地转参数,N为浮力频率或(B-V)频率,U为越山气流的速度,H为越山的高度]。在北坡F/N约为0.01,NH约为7 m·s-1,在这个地方满足判据Q<F/N,只要有7 m·s-1以上的风就不会被山脉阻滞,可以翻越过山。另外,冷空气在翻越山脊时常常会发生水汽凝结,凝结放出的潜热给越山气流提供了能量[2]。总之,对于这个700 m高差的山口,冷空气是容易翻越的。
目前对大风研究较多的主要在雷暴、强对流的大风预报[3-5],地形与大风的关系和预测多为统计和特征分析[6-8],以及气旋锋面大风的监测和诊断分析[9-10],对地形与大风的特殊关系及大风短时精细化预报研究成果较少。
通过对百里风区的特殊地形分析,根据山口的狭管效应和冷空气越山后流洩风的理论, 对百里风区强风出现的情况进行了估算和实例的验算,并利用上游指标站(木垒站)与十三间房站(百里风区风速最大测站, 原站址名为七角井站)的时间相关性分析结果建立了风速预报方程,随着自动气象观测站观测时效的加密,利用此方法对制作1小时以内的风精细化预报提供了一种思路。
1 狭管效应越山的气流进入山口后,会因地形的狭管效应而加速。百里风区的这个山口,入口处谷宽约60 km,最窄处谷宽约45 km,谷长约36 km。入谷处的海拔约为1000 m,最窄处海拔高度约为1500 m,山谷两侧的山地海拔高度约为2000 m。据文献[8]中运用的估算方法,U2=U1S1/S2+A(dT/dt)/(σS2),其中,U1为气流刚进山口的风速,U2为气流进入山谷的风速,S1为对应U1的横截面面积,S2为对应U2的横截面面积,A为从S1截面到S2截面间水平截面面积,σ是静力稳定度,dT/dt是气流运动过程中气流、气温随时间的微商。由于百里风区这个山口的地形有很多特殊的情况,一是这个山口的入口处截面较宽;二是从入口处到最窄处海拔高度一直上升;三是入口处山谷两侧山顶高度比最窄处山顶高度要低,因此在推算S1,S2时对文献[8]中所给估算方法略作修改,对于此处可得下式:
| ${U_2} = 1.86{U_1} - 2.2$ | (1) |
式中,U1是入口处风速,U2是最窄处风速。对于这个山谷,从入谷到出谷海拔高度是一直上升的,由于空气被迫抬升而绝热降温,所以第二项为负。由此这里的狭管效应对应关系可列表来表示(见表 1)。由表 1可知,越山气流由于狭管效应风速得到加大。
|
|
表 1 狭管效应风速对应关系 Table 1 The corresponding relationship of wind velocities due to the effect of narrow pipe |
冷空气越过山口后,沿斜坡地形因重力而加速下滑的风叫流洩风或称重力流。参照文献[8]中运用的估算方法,根据这个地方地形的特点作如下的推导:设冷空气沿迎风坡到最高处气团的气温为TdL,最高处的环境气温为TdH,迎风坡山脚处的气温为T1,下坡山脚处的气温为T2,冷空气翻山后沿山坡下滑距最高处距离X处气团的气温为TL,对应此处的环境气温为TH,可有下式:
| ${T_{{\rm{dL}}}} = {T_1} - {\gamma _{\rm{d}}}{H_1}$ | (2) |
| ${T_{{\rm{dH}}}} = {T_2} - \gamma {H_2}$ | (3) |
| ${T_{\rm{L}}} = {T_{{\rm{dL}}}} + {\gamma _{\rm{d}}}X{\rm{sin}}\alpha $ | (4) |
| ${T_{\rm{H}}} = {T_{{\rm{dH}}}} + \gamma {\rm{ }}X{\rm{sin}}\alpha $ | (5) |
式中,γd为干绝热垂直递减率,γ为环境气温垂直递减率,H1为迎风坡山脚到最高处的垂直高度,H2为下坡山脚到最高处的垂直高度,X轴以最高处定为原点,沿风向向下坡方向,α为下坡的坡度角。对于前文所说的地形特点,H2>H1。据文献[8]所述,由流洩风理论:
| $U\frac{{\partial U}}{{\partial X}} = g(\frac{{{\theta _{\rm{H}}} - {\theta _{\rm{L}}}}}{{\bar \theta }}){\rm{sin}}\alpha $ | (6) |
先将式(1) 和(2) 代入式(3) 和(4) 得:
| $\begin{array}{l} {T_{\rm{H}}} - {T_{\rm{L}}} = {T_2} - {T_1} - (\gamma - {\gamma _{\rm{d}}}){H_1} + \\ \quad \quad \quad (\gamma - {\gamma _{\rm{d}}})X{\rm{sin}}\alpha - \gamma \Delta H \end{array}$ | (7) |
其中ΔH= H2-H1。
| ${\rm{因}}(\frac{{{\theta _{\rm{H}}} - {\theta _{\rm{L}}}}}{{\bar \theta }}) = \frac{{{T_{\rm{H}}} - {T_{\rm{L}}}}}{{\bar T}}$ | (8) |
其中θ与T分别为从山脚到最高处的环境平均位温和气温。将式(7) 代入式(8) 后再代入式(6) 得:
| $\begin{array}{l} U\frac{{\partial U}}{{\partial X}} = \frac{g}{T}[\Delta T - (\gamma - {\gamma _d}) \times \\ \quad \quad \quad ({H_1} - x{\rm{sin}}\alpha ) - \gamma \Delta {H_2}]{\rm{sin}}\alpha \end{array}$ | (9) |
对式(9) 从X=0到X=L积分,并用Lsinα=H2代换整理得:
| $\begin{array}{l} U_j^2 = U_d^2 + 2g{H_2}\frac{{\Delta T}}{T} - 2g{H_1}{H_2}\frac{{(\gamma - {\gamma _d})}}{{\bar T}} + \\ \quad \quad gH_2^2\frac{{(\gamma - {\gamma _d})}}{{\bar T}} - 2g{H_2}\Delta H\frac{\gamma }{T} \end{array}$ | (10) |
其中,ΔT=(T2-T1)。Uj是下滑至山脚处的风速,Ud是越山气流在山口最高处的风速,g为重力加速度,γd为干绝热垂直递减率,γ为气温垂直递减率,ΔT为南北坡山脚处测站气温差,T为山脚处与山口最高处的平均绝对气温。取T=280 K,γ=0.6 ℃·(100 m)-1,γd=0.976 ℃·(100 m)-1。H1=600 m, 由于这个山口南坡坡度比北坡大,到十三间房车站高差约900 m,H2=900 m。根据式(3),给出不同的ΔT和Ud可对Uj进行估算,估算结果见表 2。
|
|
表 2 流洩风效应风速Uj、温差对应关系(单位:m·s-1) Table 2 The relationship among wind velocity and temperature difference due to the effect of drainage winds (unit: m·s-1) |
表 2中,考虑到是冷空气入侵过程,再者加上南北坡山脚处的垂直落差300 m的地形,ΔT≥5℃。另外,考虑到翻越山口的气流因狭管效应得到加速,Ud≥10 m·s-1。对应表中的数字是气流到达南坡山脚处的风速Uj。由表 2可看出,ΔT越大,流洩风的风速越大。据文献[2]中所述,在山口南坡因常年风蚀构成的南北向的干沟也垂直对着铁路。这些干沟又会对下滑的气流产生狭管效应,从而使气流再度加速。所以,根据以上的推算出的风速会比实况小些。
3 实例的验算和分析以2008年10月20日的实况来验证。20日10时山口北坡的西边木垒站风速为16.3 m·s-1,假设进入山口的风速与其相等的话,翻越山口时由于狭管效应的作用,可加速到28 m·s-1。这次过程为一次强冷空气入侵过程,20日08时十三间房与木垒的温差为5.5℃,14时温差为14.0℃,取ΔT为10℃。冷空气沿坡下滑再次得到加速,按表 2中查得风速为36.6 m·s-1。实况是:20日19时十三间房风速为37.1 m·s-1。估算的略偏小些。
由以上验算,可知处于上游的木垒的风速与处于下游的十三间房的风速前后是有关联的。分别用2010—2011年春季等多次典型大风过程的木垒和十三间房逐小时风速资料,可计算同时及延时1~20小时的相关系数,多次天气过程大多以9~10小时相关系数最大,结果如图 1。

|
图 1 木垒和十三间房车站风速延时1~20小时相关系数分析图 Fig. 1 Correlation coefficient chart of 1-20 h delay of wind velocity at Mulei and Shisanjianfang Stations |
由图 1可看出以延时10小时的相关系数为最大,延时9、10和11小时的相关系数分别为0.6963、0.7465和0.7365。这就可以给出一个启示,在冷空气入侵的过程中,可用木垒的风速预报9小时后十三间房的风速,预报时效可达9小时,预报精度为小时。如果将两地的观测精度提高到20分钟,预报精度还会提高。在冷空气入侵过程中,这种用上游邻近站的要素做某地要素精细化预报,可能是一个简单易行的方法。利用前9~11小时木垒的风速作因子,建立回归方程:
| $\begin{array}{l} Y = 0.261188{X_{ - 9}} + 0.75717{X_{ - 10}} + \\ \quad \quad 0.776202{X_{ - 11}} + 12.47958 \end{array}$ |
其复相关系数为0.764298,预报拟合情况见图 2。
|
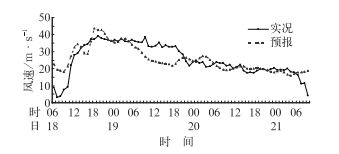
图 2 2010年1月18—21日十三间房预报与实况对比图 Fig. 2 Comparison between forecast (dashed) and observation (solid) at Shisanjianfang Station from 18 to 21 January 2010 |
由图 2可见,预报与实况总体趋势吻合较好,风速极大值出现的时间预报准确,量级相当。用这种方法建立的回归方程其物理意义是明显的。
4 效果检验利用上述方法,用2011年1—5月中旬期间实测资料对十三间站19场大风天气进行了逐时预测,以达到17 m·s-1为大风标准,大风的预报准确率达72.2%;有大风时风速的平均绝对误差为7.1 m·s-1;极值出现时间平均比预报偏晚2.2小时, 最大极值平均误差6.7 m·s-1, 对极值的出现时间和量级有一定的参考价值。
5 结论(1) 以上分析提供了一种风要素的精细化预报思路和方法。
(2) 从以上的分析和估算中可以得到这样的结论:虽然造成大风的根本原因是冷空气活动,但特殊的地形影响加大了风速。百里风区就是越山的冷空气因狭管效应和流洩风作用而形成的强风区。
(3) 从表 2中可看出,Uj随ΔT的增大而增大。也就是说入侵的冷空气越冷,背风坡山脚处的气温越高时流洩风的风速越大。在冬季,由于近地层逆温层的出现,背风坡山脚处的气温不高,所以在这个季节流洩风的作用大为减弱,这也解释了为什么百里风区强风灾害以春夏季为最多。
(4) 效果检验预报准确率较高,尤其是对极大风速出现的时间和量级具有一定的参考价值。
(5) 以上所述,仅从冷空气越山沿坡面下滑所产生的流洩风角度来论述的。而且关注的仅是地面风。对于背风坡的流场的二维(X,Z)情况是比较复杂的。要根据称作Scorer参数的
杨国祥, 何齐强, 陆汉城, 1991. 中尺度气象学[M]. 北京: 气象出版社, 218-220.
|
新疆短期天气预报手册[M]. 乌鲁木齐: 新疆人民出版社, 1986: 279.
|
钟利华, 曾鹏, 李勇, 等, 2011. 广西雷暴大风环流特征和物理量诊断分析[J]. 气象, 37(1): 59-65. DOI:10.7519/j.issn.1000-0526.2011.01.007 |
廖晓农, 于波, 卢丽华, 2009. 北京雷暴大风气候特征及短时临近预报方法[J]. 气象, 35(9): 18-28. DOI:10.7519/j.issn.1000-0526.2009.09.003 |
朱君鉴, 刁秀广, 曲军, 等, 2008. 临沂强对流灾害性大风多普勒天气雷达产品分析[J]. 气象, 34(12): 21-26. DOI:10.7519/j.issn.1000-0526.2008.12.003 |
刘敏, 孙杰, 杨宏青, 2010. 湖北省不同地形条件下风随高度变化研究[J]. 气象, 36(4): 63-67. DOI:10.7519/j.issn.1000-0526.2010.04.011 |
辽宁省复县气象站, 1975. 我站的偏北大风预报[J]. 气象, 1(2): 15-15. DOI:10.7519/j.issn.1000-0526.1975.02.007 |
祝学范, 2004. 大风出现的位置与地形的关系[J]. 新疆气象, 27(6): 1-2. |
顾光芹, 田国强, 李元华, 等, 2011. 曹妃甸工业区最大风速资料重建及检验[J]. 气象, 37(8): 1018-1025. DOI:10.7519/j.issn.1000-0526.2011.08.014 |
Kato W, Suzuki H, Shimamura M, et al. The design and initial testing of an X band Doppler radar for monitoring hazardous winds for railroad system[C]. Preprints, 33rd Conf on Radar Meteorology, Cairns, Australia, Amer Meteor Soc 2007, P13A.15.
|
 2012, Vol. 38
2012, Vol. 38 