受全球及区域尺度气候变化影响,北京城市极端天气气候事件明显增多,区域经济社会已表现出高度的敏感性[1-2]。并且,随着北京城市化发展,不透水地面大幅度增加,致使相同降雨条件下的径流系数增大,洪峰提前,洪量增大[3],城市暴雨造成的内涝积水现象时有发生,对城市排水和河道行洪构成巨大的压力。2001年以来,北京已经出现多次由于雨雪天气引起的交通严重堵塞和大面积交通瘫痪事件。这对城市排水管网设计、改造、城市防洪体系建设提出了新的挑战。
由于气候变化引起的降水频率及空间分布的变化,以及北京城市建设飞速发展的影响,原有的城市雨水排除规划设计标准已经不能满足现在的城市发展现状,应针对目前状况研究修订适合北京城市发展的雨水排除规划设计标准。
为此,本文分析在气候变化和城市化发展大背景下,北京市降水的空间分布和时间变化规律,对降雨进行分区研究,并选取代表站,分析北京市不同历时强降水重现期,为北京市雨水规划设计标准的修订提供参考依据。
1 资料来源本文采用的资料为:(1) 北京市观象台1841-2008年共168年年降雨量资料。(2) 北京地区20个气象站(海淀、朝阳、观象台、丰台、顺义、汤河口、密云、怀柔、上甸子、平谷、通州、大兴、斋堂、门头沟、房山、霞云岭、延庆、昌平、佛爷顶、石景山)近50年逐日降水量资料。(3) 北京地区遍布全市的82个雨量站不同历时降水量资料。(4) 北京市观象台1941-2008年逐分钟降雨量资料。资料来源于自记降水记录纸,在降水自记纸的数字信息化过程中,已对降水自记迹线和时间、自记纸的扫描、数据的提取等进行了人工检测,即严格质量控制[4]。
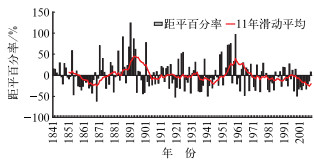
2 北京地区降水量时空分布特征 2.1 长期和短期降水量时间变化特征从北京观象台1841-2008年年降水量线性趋势演变图(图 1)可见:近168年,北京地区有两个多雨时段,分别是1871-1894年和1947-1960年;两个少雨时段:1853-1870年和1992年至今,目前北京市处于20世纪90年代至今的少雨时段内。
|
图 1 北京观象台降水量距平百分率及其11年滑动平均演变 Fig. 1 The precipitation anomaly percentage of Beijing and its 11-year moving average |
从图 1还可看出,近百年北京地区降雨量的年际波动较大,年降水量介于242~1406 mm之间,其变率达0.58,这表明北京的年降雨容易产生重大的偏离,以致出现旱涝无常的状况[5]。近50年,北京地区年降水量呈减少趋势,减少速率为31 mm/10 a。尤其是1999-2007年为连续偏少年,年平均降水量仅为462.1 mm,比近30年平均(556.0 mm)偏少17%。近50年降水最少的3个年份分别为1999,1965和2006年。
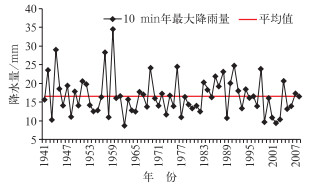
从北京观象台1941-2008年10 min年最大降雨量变化趋势(图 2)可以看出,10 min年最大降雨量年际间差异较大,最大值主要集中在20世纪50年代末至60年代初和80年代。其中,1944、1957和1959年最高,10 min雨量在28~35 mm之间。从90年代初至今,10 min年最大降雨量呈减小的趋势,1999-2008年10 min平均年最大降雨量仅为13.7 mm,比常年值偏少了17%。
|
图 2 观象台1941-2008年10 min最大降水量变化 Fig. 2 The annual maximum 10 min rainfall trend at Beijing Observatory during 1941-2008 |
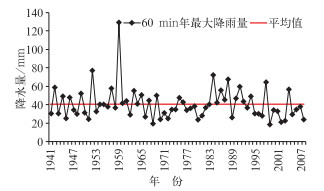
同10 min年最大降雨量趋势类似,1941-2008年观象台60 min雨强的年际差异明显,从18.2~129.7 mm/60 min。20世纪50年代和80年代的60 min年最大降雨量最大(图 3),从1984年至今,60 min雨强呈明显减小的趋势,60 min雨强减小的趋势达到11 mm/10 a,其变化趋势接近0.1的显著性检验水平。
|
图 3 观象台1941-2008年60 min最大降水量变化 Fig. 3 The annual maximum 60 min rainfall trend at Beijing Observatory during 1941-2008 |
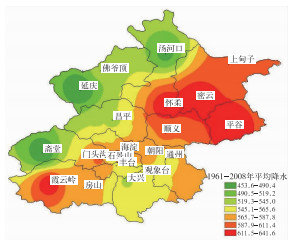
北京地区年降水量的空间分布与地形高度关系密切,汛期偏南风到来时由于地形的抬升,山前的迎风坡一带容易产生较大的降雨[6-7],密云、怀柔、霞云岭是多雨区,山后的背风区为少雨区。从北京地区1961-2008年平均年降水量分布图(图 4)得出,北京的降水量大值区大致与地形分布相一致,呈东北-西南走向,降水量≥600 mm的高值区分布在北京的东北部和西南部,降水量500~600 mm的高值区主要分布在城市中心,降水量<500 mm的低值区分布在西部山区和燕山山后的延庆等地。
|
图 4 1961-2008年北京地区年平均降水量分布 Fig. 4 The annual rainfall distribution (unit:mm) in Beijing averaged over 1961-2008 |
分析北京地区20个气象站年代际降水量的分布得出(图 5), 位于怀柔、密云附近的≥600 mm降水量等值线的范围随年代发生明显改变,20世纪80年代降雨中心主要位于怀柔、密云一带,90年代降雨中心逐渐向东南移动,城区北部的降水量逐渐增加。另外,位于房山的霞云岭附近出现一个降水高值区。北京的主要降水落区呈东北-西南向分布,2000年之后降水中心量值减少非常明显,中心位置回撤到密云附近。
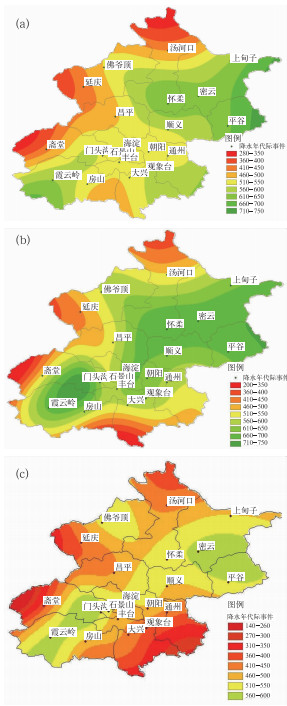
|
图 5 北京地区年代际平均降水量分析 (a) 1981-1990年, (b) 1991-2000年, (c) 2001-2008年 Fig. 5 The distributions of annual mean precipitation (unit:mm) in Beijing averaged over (a) 1981-1990, (b) 1991-2000 and (c) 2001-2008 |
从北京地区20个气象观测站近30年降水量趋势(图略)得出,全市各站降水均呈减少趋势,东部地区减少最为明显,减少趋势为40~50 mm/10 a。
2.2.2 短历时强降雨空间分布的变化特征分析应用北京市遍布全市的82个雨量站1971-2008年60 min年最大降雨量资料,分析了北京地区短历时强降雨空间分布的变化特征(图 6)。由图可见,1971-1980年,北京地区强降雨主要为全市区域性降雨。1991年至今,短历时强降雨呈现出局地性的特征,降水分布不均,强降水中心大致成东北-西南向带状分布。
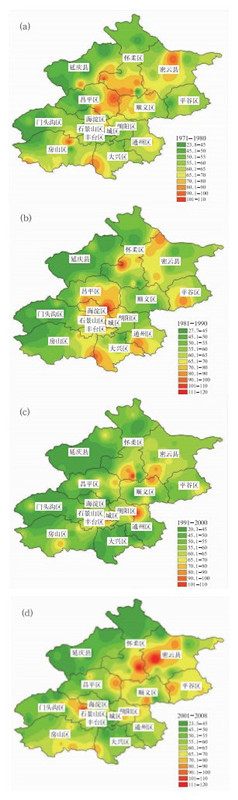
|
图 6 北京地区各年代60 min最大雨强的空间分布 (a)1971-1980年,(b) 1981-1990年,(c) 1991-2000年,(d) 2001-2008年 Fig. 6 The spatial distributions of maximum 60 min rain intensity (unit: mm·h-1) in Beijing for different decades: (a) 1971-1980, (b) 1981-1990, (c) 1991-2000 and (d) 2001-2008 |
通过分析北京地区区域性大雨发生的频次(一次降水过程中20个气象站中有超过40%的台站出现大雨)可以看出(图 7),20世纪60年代和70年代发生区域性大雨的频次较高,70年代最为明显,一次大雨过程可以导致区域内大范围台站24小时之内同时出现大于25 mm的降水。但由于当时经济发展还处于起步阶段,城市化发展还较为落后,不透水地面面积较小,道路交通和灾害监测远不如今日迅捷发达,区域性大雨带来的损失不如今日明显。80年代后,一方面北京地区的降水明显偏少,另一方面,发生区域性大雨的频次也明显减小。近年来北京暴雨多呈现出局地性特征,这种强对流天气形势是一个个雨团作用引起的,具有随机性,发展快速的特点,不仅容易引发交通瘫痪、使市民出行受到影响,而且给暴雨预报增加了很大的难度。
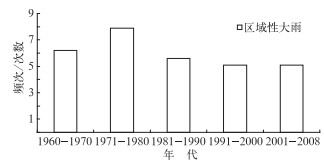
|
图 7 北京地区区域性大雨频次趋势 Fig. 7 The frequency of heavy rain in Beijing region for different decades |
根据区域气候、水文特征和自然地理条件,采用数理统计分析方法对北京降雨进行区域划分,目的是从空间上揭示北京不同区域降雨分布的相似与差异、共性与个性。选取北京市82个雨量站1971-2008年汛期(6-9月)、60 min和1440 min历时降水量资料进行分析。
采用主成分分析[8]对全市1971-2008年汛期降雨量资料进行标准化处理后进行分解。前三个特征向量方差贡献率分别为66.09%、7.33%、3.34%,基本代表了北京地区降水变化及其空间分布的基本特征,其余特征向量方差贡献均较小,不作分析。
第一特征向量呈全区一致型,这表明北京地区受大尺度天气系统影响,降水在空间上具有很好的一致性,即全市一致的多雨或少雨(图 8a)。
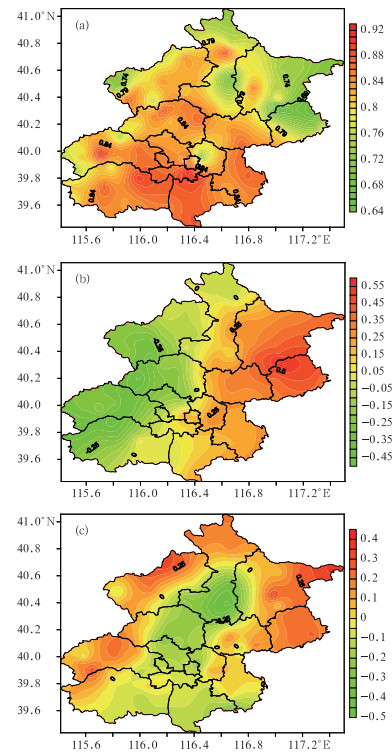
|
图 8 1971-2008年汛期降雨量EOF第一(a)、第二(b)和第三特征向量(c) Fig. 8 The first (a), second (b), and third (c) eigenvectors of the 1971-2008 annual flood season rainfall EOF analysis |
第二特征向量的空间分布大致为东西符号相反型(图 8b),零线的走向基本与燕山山脉重合。
第三特征向量为城市中心区和南部平原地区为负值,而北部山区为正值,反应出山坡地形对降水的影响,另外,城市化的加强加上地形的共同作用也使得降水落区集中在山前南坡,第三特征向量的空间分布反映了平原区与东北部山区和山后区的差别(图 8c)。
通过分析3个主成分向量可以总结出:在大的空间尺度上,北京地区降雨应分为1个区。在考虑地形和城市化尺度上,北京应分为4个区,分别是山后区、东北部山区,城市中心区和南部平原区,具体分区结果如下(图 9),反映出山前迎风坡跟山后背风坡的区别。
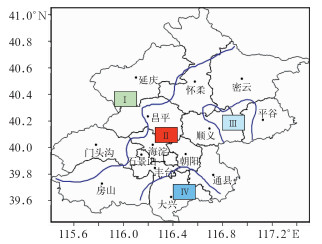
|
图 9 北京市降雨分区示意图 Fig. 9 The schematic deiagram of the 4-subregion precipitation in Beijing |
对各分区雨量站点进行统计,结果如表 1所示。其中,Ⅰ区60 min年平均降雨量为23.3 mm;Ⅱ区60 min平均降雨量为37.9 mm;Ⅲ区和Ⅳ区60 min平均降雨量稍低于Ⅱ区,为34.1和34.7 mm。Ⅱ区为城市中心区,由于城市化影响及地处山前迎风区,Ⅱ区的60 min降雨量和1440 min降雨量均大于其他三个区。因此,在分析城市雨水排除设计标准时,应重点分析Ⅱ区的降雨情况。结合各区域内代表气象站的资料年代及建站位置考虑,Ⅰ区代表气象站为延庆站,Ⅱ区为北京市观象台站,Ⅲ区为密云站,Ⅳ区为大兴站。
|
|
表 1 各分区降雨量统计(单位:mm) Table 1 Rainfall statistics in 4 subregions of Beijing (unit: mm) |
引入广义偏态分布方法(GPD)对北京城区代表站的短历时降雨进行拟合分布研究。
4.1.1 广义偏态分布模型介绍近年来,广义偏态分布方法(Generalized Pareto Distribution, GPD)已得到普遍应用[9]。自1975年Pickands将这一分布模型引入到水文气象学研究中,Hosking等[10]分别进一步发展了该模型的应用。GPD方法的最大优点在于,它直接由原始资料数据(如历年)以给定门限值为标准来抽取(每年)超过该门限值的极大(或极小)值,即用所谓“超门限峰值”(Peaks Over Threshold, POT)方法抽样,其所需资料年限大大节省,从而增加了极值的样本量,克服了广义极值分布GEV或Gumbe1分布采用所谓“单元极值”(Block Maxima, BM)或“年极值”(Annual Maxima, AM)抽样方法的缺点[11]。由于GPD参数的概括性(门限值、尺度参数和形状参数),在不同阈值下它与指数分布、Beta分布和Pareto分布具有对应关系。从应用意义上说,主要用于描述超过某特定临界值(即门限值)的全部观测值资料集(例如,超过临界水位的洪水、大于某临界值的日(时)、候、旬或月的降水量或大于某临界值的阵风风速)等的概率分布特征。
广义偏态分布(GPD)函数[12]为:
| $ \begin{array}{l} F\left( x \right) = 1 - {\left[{1-\kappa \left( {\frac{{x-\zeta }}{\alpha }} \right)} \right]^{1/\kappa }}\\ \kappa \ne 0, \zeta \le x \le \frac{\alpha }{\kappa } \end{array} $ | (1) |
分布密度函数(PDF)为:
| $ f\left( x \right) = \left( {\frac{1}{\alpha }} \right){\left[{1-\kappa \left( {\frac{{x-\zeta }}{\alpha }} \right)} \right]^{\frac{1}{\kappa } - 1}} $ | (2) |
式中的分布参数ζ称之为门限值,α称之为尺度参数,κ为线型参数或形状参数。
GPD的重现期值公式为:
| $ {x_T} = \zeta + \frac{\alpha }{\kappa }\left[{1-{{\left( {\lambda T} \right)}^{-\kappa }}} \right] $ | (3) |
对于极值分布参数估计常用矩法,最小二乘法和极大似然法等。近年来,发展起来的概率加权矩法(PWM)用于估计极值分布的参数,不但有较高的精度可与公认的“极大似然法”相媲美,而且其计算简便易行,不需要利用繁琐的迭代计算。丁裕国等[13]在国内率先引用该方法已取得明显效果。目前,国际上已进一步采用PWM的线性组合即所谓L-矩法拟合各种极值分布,这种参数估计的精度更高并具有统计稳健性,近年来,有学者在国内率先采用该估计方法拟合降水的极值分布,取得了显著的效果[14]。
4.1.3 GPD分布对北京观象台短历时降水拟合检验对于概率分布模拟来说,样本量的大小和分布是否合理是模拟效果好坏的关键,通过对观象台5 min最大降雨量进行广义偏态分布模拟(图 10)可以看到,测试数据与模型模拟的程度很高,概率散点图模型重新排列的数据基本都能落在模拟线上(图 10a),从百分位散点图的拟合效果来看,在尾部模式模拟的结果与实测的情况有所误差,但总体来说,5 min降雨极值模拟符合GPD分布(图 10b)。通过GPD分布结果的重现期水平图(图 10c)得出,模拟的重现期基本都在置信区间内,也证明了GPD方法的可信度。这个特点对于120 min历时降雨的模拟也同样存在(图 11)。
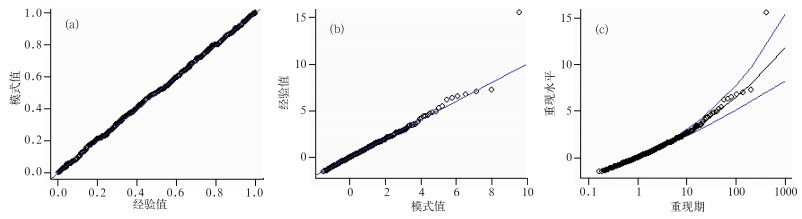
|
图 10 GPD方法对观象台5 min降雨的拟合结果 (a)概率散点图,(b)百分位散点图,(c)重现期水平图 Fig. 10 The 5 min rainfall fitting results with the GPD method in terms of (a) probability, (b) quantile, and (c) return period level |
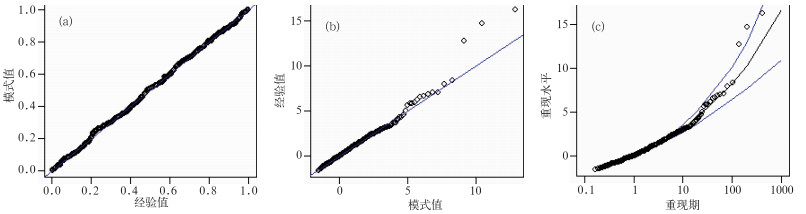
|
图 11 GPD方法对观象台120 min降雨的拟合结果 (a)概率散点图,(b)百分位散点图,(c)重现期水平图 Fig. 11 Same as in Fig. 10, but for the 120 min rainfall fitting results |
应用科斯检验方法(Kolmogorov-Smirnov)[15]对GPD模拟效果进行检验,研究样本观察值的分布和设定的理论分布是否吻合。科斯检验的公式如下:
| $ {D_{\max }} = \max \left| {{S_n}\left( x \right) - {F_0}\left( x \right)} \right| $ | (4) |
式中,Sn(x)为n次观察的随机样本观察值的累积概率分布函数,即经验分布函数,F0(x)为特定的累积概率分布函数,即理论分布函数。若对每一个x值来说,Sn(x)与F0(x)差异很小,则表明经验分布函数与特定分布函数的拟合程度很高。
由表 2可见,GPD方法对各历时降雨的拟合非常好,不同历时的科斯检验结果均小于0.05,且具有很高的相关性,表明GPD方法对不同重现期下不同历时降雨量的估算结果可信。
|
|
表 2 观象台不同历时降雨GPD分布拟合效果检验 Table 2 The fitting test of different duration rainfall at Beijing Observatory with GPD method |
根据暴雨分区结论,应用GPD方法预估北京城区代表气象站(观象台)不同历时的重现期变化如表 3。
|
|
表 3 观象台不同历时重现期降雨量(单位:mm) Table 3 Precipitation in Beijing Observatory return period of different duration (unti: mm) |
通过观象台不同历时重现期模拟结果(表 3)与北京市现行水文重现期标准[16]进行对比,各重现期降雨量标准基本吻合,各历时降雨重现期模拟符合实际排水设计要求,可为暴雨强度公式的设计提供参考。
5 结论本文通过对北京地区气象站及雨量站多个历时降水量资料的分析,可以得到以下结论:
(1) 北京观象台1841-2008年年降水量线性趋势显示:北京地区有两个多雨时段:1871-1894年、1947-1960年;两个少雨时段:1853-1870年、1992年至今。
(2) 北京地区年降水量的大值区大致与地形分布相一致,呈东北-西南走向。20世纪80年代降雨中心主要位于怀柔、密云一带。90年代降雨中心逐渐向东南移动,城区北部的降水量逐渐增加。另外,位于房山的霞云岭附近出现一个降水高值区。2000年之后降水中心量值减少非常明显,中心位置回撤到密云附近。
(3) 1941-2008年观象台短历时10 min和60 min年最大降雨量的高值主要集中在20世纪50年代至60年代。80年代中期至今,短历时年最大降雨量呈减小的趋势。
(4) 20世纪70年代至80年代,北京地区短历时强降雨主要为全市区域性强降雨,90年代之后北京的短历时强降雨呈现出局地性的特征,降水分布不均,强降水中心大致成东北-西南向带状分布。
(5) 根据北京市降雨空间分布及EOF分析,将北京市划分为4个降雨分区,分别为:山后区、东北部山区,城市中心区和南部平原区。
(6) 应用广义偏态分布方法对城区代表站观象台不同历时重现期雨量进行模拟,并与现行排水规范进行对比,结果表明,重现期模拟结果可靠。
代刊, 何立富, 金荣花, 2010. 加密观测资料在北京2008年9月7日雷暴过程分析中的综合应用[J]. 气象, 36(7): 160-167. DOI:10.7519/j.issn.1000-0526.2010.07.023 |
施洪波, 2011. 1960—2000年京津地区夏季高温日数的变化趋势分析[J]. 气象, 37(10): 1273-1282. |
辛格(V. P. Singh)著, 赵卫民等译. 水文系统流域模拟[M]. 郑州: 黄河水利出版社, 2000.
|
李建, 宇如聪, 王建捷, 2008. 北京市夏季降水的日变化特征[J]. 科学通报, 53(7): 529-532. |
高善明, 张义丰, 2007. 北京自然环境与都城变迁[M]. 气象出版社.
|
孙继松, 杨波, 2008. 地形与城市环流共同作用下的β中尺度暴雨[J]. 大气科学, 32(6): 1352-1364. |
孙继松, 2005. 气流的垂直分布对地形雨落区的影响[J]. 高原气象, 24(1): 62-69. |
魏凤英, 1999. 现代气候统计诊断与预测技术[M]. 北京: 气象出版社.
|
江志红, 丁裕国, 朱莲芳, 等, 2009. 利用广义帕雷托分布拟合中国东部日极端降水的试验[J]. 高原气象, 28(3): 573-580. |
Hosking J R M, Wallis J R, 1987. Parameter and Quantile Estimation for the Generalized Pareto Distribution[J]. Technometrics, 29: 339-349. DOI:10.1080/00401706.1987.10488243 |
Ding Yuguo, Chen Binyan, Jiang Zhihong, 2008. A newly discovered GPD-GEV relationship together with comparing their models of extreme precipitation in summer[J]. Advance in Atmospheric Sciences, 25(3): 507-516. DOI:10.1007/s00376-008-0507-5 |
Brabson B B, Palutikof J P, 2000. Tests of the generalized Pareto distribution for predicting extreme wind speeds[J]. J Applied Meteor, 39: 1627-1639. DOI:10.1175/1520-0450(2000)039<1627:TOTGPD>2.0.CO;2 |
丁裕国, 刘吉峰, 张耀存, 2004. 基于概率加权估计的中国极端气温时空分布模拟实验[J]. 大气科学, 28(5): 771-782. |
蔡敏, 丁裕国, 江志红, 2007. 我国东部极端降水时空分布及其概率特征[J]. 高原气象, 26(2): 309-318. |
Sangeeta Biswas, Shamim Ahmad, M Khademul Islam Molla, et al, 2008. Kolmogorov-Smirnov test in text-dependent automatic speaker identification[J]. Engineering Letter, 16: 4. |
北京市水利局, 北京市水文手册(第一分册)-暴雨图集[M]. .
|
 2012, Vol. 38
2012, Vol. 38 
