2. 甘肃省天水市气象局,天水 741000
2. Tianshui Meteorological Office of Gansu, Tianshui 741000
陕西渭北黄土高原地区是符合苹果生产气象指标的优生区之一,是中国苹果产业带的重点建设地区。据统计,2009年陕西省苹果园面积达56.7×104 hm2,产量805×104 t,占世界苹果总产量1/8,中国总产量1/3。苹果面积和产量双获全国第一,是全国乃至世界集中连片面积最大的优质苹果生产基地。然而,每年9—10月苹果成熟期间,陕西处于西太平洋副热带高压边缘的西南气流里,当北方冷空气逐渐活跃,南下次数增多的情况下,经常发生连阴雨天气,影响苹果着色和品质的形成[1]。因此做好果业陕西苹果基地县连阴雨灾害的预测,对防灾减灾和发展陕西果业生产意义重大。
陕西苹果果区连阴雨多发于每年9—10月,为期两个月[2]。而9月中旬至10月上旬恰逢苹果摘袋、着色和采收时期,过长时间的阴雨天对苹果的品质和产量影响显著。有研究结果表明[3-5],充足的光照对苹果着色至关重要,在果实着色期,果实获全日照70%以上时果面全红;获全日照40%~70%时果面部分红;获全日照30%以下时果实不着色。例如2007年9月底至10月初,陕西苹果果区各果业基地县遭遇9~15天连阴雨天气过程,使果园气温偏低、湿度过大、太阳光照严重不足,造成苹果着色率和着色度下降,果面光滑度下降,果面不洁等后果,严重影响苹果品质,果农经济效益进而严重受损。
目前,有关陕西连阴雨的研究已取得不少成果[6-11],用于连阴雨的预报方法也较多。本文试图从简便实用、便于果业气象服务的业务应用角度出发,设计一种新的连阴雨指数,并通过典型K阶自回归预测模式,对陕西12个在地理位置、生态环境、气候特点和苹果生产水平具有代表性的基地县进行连阴雨强度预测,旨在提高对陕西苹果基地县连阴雨的短期气候预测能力,实现连阴雨灾害的分区定量预报。为陕西果业生产、防灾减灾及进一步拓宽果业气象服务提供技术支撑。
1 资料来源选取陕西白水、彬县、澄城、淳化、凤翔、合阳、洛川、礼泉、蒲城、旬邑、延安和耀县12个站1961—2009年每年9月中旬至10月上旬的≥3 d降水日数和无降水日数(白水、合阳、耀县1962年建站,故资料从1962年起),作为设计连阴雨指数的基本气象资料。
2 连阴雨指数设计陕西省对连阴雨天气的定义为测站连续4 d及以上,日降水量大于或等于0.1 mm,且测站过程降水大于20 mm的降水天气。而在近10年的苹果气象服务中,笔者发现在苹果摘袋、着色和采收时期,尤其是着色和采收期,持续3天的连阴雨,以及连阴雨或连阴天所带来的低温天气即可对苹果着色、果面光滑度产生影响,且影响程度随连阴雨天气长度的增加而增加,但与过程降水量的多寡关系不大。所以为了能够反映连阴雨天气长度对苹果摘袋、着色和采收的影响强度,我们设计如下表达式来定义连阴雨指数:
| ${L_u} = {N_{r \ge 3}}/{N_{R = 0}}$ | (1) |
其中Lu为连阴雨指数;Nr≥3为9月中旬至10月上旬降水(R≥0.1 mm)连续3天及以上的日数,该日数越多,连阴雨危害越重;NR=0为9月中旬至10月上旬无降水日数,该日数越多,连阴雨危害越轻。
3 连阴雨指数的时空分布将用式(1) 算得的连阴雨指数与果业基地县历史连阴雨资料记载进行比对[12-13],有85%左右的连阴雨指数能够较准确地反映当年的连阴雨状况,说明这种连阴雨指数能够较客观地反映连阴雨强度。
如图 1a和1b所示,在时间分布上,陕西12个苹果(梨)基地县的连阴雨指数的强度在20世纪60年代为持续下降趋势,70年代初到80年代末各果业基地县连阴雨指数强度变化幅度较大,自90年代初突然变强、回落并再次缓慢增强后,于2000年后维持在中等强度水平。在空间分布上,渭北西部和关中西部基地县的连阴雨指数整体略高于延安及渭北东部基地县。其中凤翔、淳化和洛川一带连阴雨指数总体偏高,说明这些地区的连阴雨强度偏强,连阴雨对苹果成熟期的影响较其他基地县更为严重。这与陕西果业基地县9—10月连阴雨气候特征[14]基本一致。
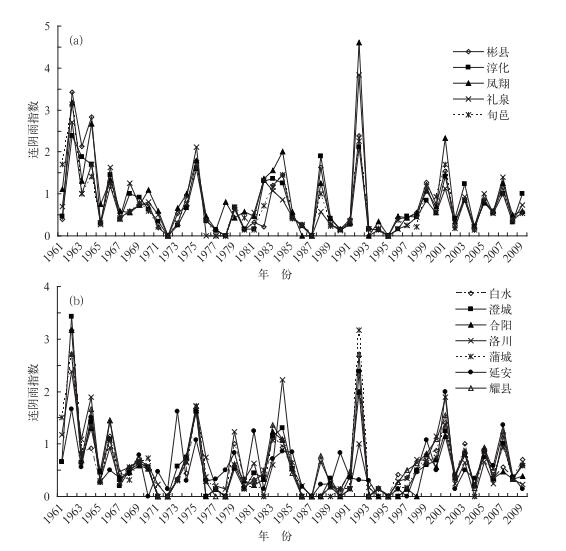
|
图 1 陕西苹果生产基地县连阴雨指数的年际变化 (a)渭北西部、关中西部果区, (b)渭北东部、延安果区 Fig. 1 The annual index of continuous rainfall days (ICRD) in major apple cultivating counties of Shaanxi (a) west of Weibei and west of Guanzhong apple cultivating towns, (b) east of Weibei and Yan’an apple cultivating towns |
根据陕西连阴雨气候背景特点以及陕西省自然灾害纪实,参考其中连阴雨等级的频率分布特点,来确定连阴雨指数的频率分布,使其接近连阴雨气候背景特征。然后将12个基地县的连阴雨指数分成强、偏强、中等、偏弱和弱5个等级,详见表 1。
|
|
表 1 陕西苹果基地县连阴雨指数分级 Table 1 The grade of the index of continuous rainfall days (ICRD) in major apple cultivating counties of Shaanxi |
利用气象要素自身年变化具有准周期性和自忆性的自相关关系,建立自回归预测模式[15-20]。
设连阴雨指数时间序列为{xi}, 在最大似然比的意义下,样本的自相关(也叫退相关)系数:
| ${R_K} = \frac{{2\sum\limits_{i = 1}^{N - K} {({x_{i + K}} - {{\bar x}_K})({x_i} - {{\bar x}_0})} }}{{\sum\limits_{i = 1}^{N - K} {{{({x_{i + K}} - {{\bar x}_K})}^2}} + \sum\limits_{i = 1}^{N - K} {{{({x_i} - {{\bar x}_0})}^2}} }}$ | (2) |
式中,xK是因子的平均值;x0是预测对象的平均值。
| $\begin{array}{*{20}{c}} {{{\bar x}_K} = \frac{1}{{N - K}}\sum\limits_{i = 1}^{N - K} {{x_i}} ,}&{{{\bar x}_0} = \frac{1}{{N - K}}\sum\limits_{i = K + 1}^N {{x_i}} } \end{array}$ | (3) |
K为自相关的阶数,N为样本数。当N=49时,一般取K=1~30阶。
将用式(2) 算得连阴雨指数序列的RK,选取绝对值最大者|RK|max, 做显著性检验。取α=0.05,当自由度f=N-K-1=20时,RK的临界值|RK|2α=0.359;当f=30时,|RK|2α=0.296。若算得的|RK|max≥|RK|2α,说明自相关关系显著,可以建立K阶自回归预测模式。用最小二乘法得出K阶自回归模式
| $\hat Y = a + b{X_K}$ | (4) |
式中,
| $\left\{ \begin{array}{l} \hat b = \frac{{\sum\limits_{i = 1}^{n - K} {\left[ {{{\left( {{x_K}} \right)}_i} - {{\bar x}_K}} \right]\left[ {{{\left( {{x_0}} \right)}_i} - {{\bar x}_0}} \right]} }}{{\sum\limits_{i = 1}^{n - K} {{{\left[ {{{\left( {{x_K}} \right)}_i} - {{\bar x}_K}} \right]}^2}} }}\\ \hat a = {{\bar x}_0} - \hat b{{\bar x}_K} \end{array} \right.$ | (5) |
根据12个基地县1961—2009年,49年连阴雨指数序列,用上述统计方法和式(5) 建立各基地县连阴雨指数K阶自回归模式见表 2。
|
|
表 2 各基地县连阴雨指数K阶自回归模式(α=0.05) Table 2 The K-order autoregressive forecasting models at different counties of Shaanxi (α=0.05) |
从表 2可以看出,所选的RK,除彬县和耀县|RK|max不能通过显著性检验外,其他10个基地县均大于RK的临界值,所以建立自回归预测模式是合理的。用RK通过显著性检验的自回归模式,即可对2010年9月中旬至10月上旬10个基地县的连阴雨指数作出预测。另外,自回归模式的优点是无须选择预报因子,建模简捷,且能随气象资料的增加逐年更新预测模式,便于业务使用,作为气象灾害分区定量预测有一定的优越性。
4.3 独立样本预测试验为了检验自回归预测模式的预报效果,依4.2的统计方法建立预测模式,对2007、2008和2009年的连阴雨指数作独立样本预测试验,共得到30个预测结果,并均通过α=0.05的显著性检验。经与实际连阴雨指数比较,其中预测的连阴雨等级与实际连阴雨等级一致的有14个,相差一级的有11个,相差两级的有5个,没有相差三级及以上的。若将预测的结果按三级评定:一致的和相差一级的视为预测准确和基本准确,达83.3%,相差两级的视为预测不准确,为16.7%,相差三级的视为预测错误,为0%。从表 3可知,该预测模式能较客观地反映出陕西苹果生产基地县的连阴雨强度和趋势,具有一定的预测能力。
|
|
表 3 自回归预测模式预报效果检验 Table 3 The result of the K-order autoregressive forecasting model |
(1) 以能够反映连阴雨天气长度对苹果成熟期的影响强度为指标,设计出物理意义明确的一种新的连阴雨指数,不仅使连阴雨灾害的概念得到扩展,且计算方法简便,计算结果与历史连阴雨记载资料基本一致,能够较客观地反映出各基地县的连阴雨强度。
(2) 陕西苹果生产基地县的连阴雨强度20世纪60年代为持续下降趋势,70年代初到80年代末各果业基地县连阴雨指数强度变化幅度较大,自90年代初突然变强、回落并再次缓慢增强后,于2000年后维持在中等强度水平。
(3) 根据连阴雨强度区域分布特点,渭北西部和关中西部果区应加强在苹果摘袋后铺设反光膜并进行摘叶转果、水肥管理等措施,以提高果品的着色度、果面光滑度等品质指标。
(4) 各苹果基地县连阴雨指数自相关系数计算结果中,除彬县和耀县|RK|max不能通过显著性检验外,其他10个基地县均能通过α=0.05的显著性检验,所以建立自回归预测模式是合理的。并且,独立样本预测试验结果表明,用典型K阶自回归模式预测连阴雨强度准确和基本准确率达到83%左右,具有较好的预测能力。
(5) 该建模简捷,模式能逐年更新,使用方便,对于陕西省主要苹果生产基地县连阴雨短期天气分区、定量预报具有实用价值。当然该指数在设计时,考虑到在业务服务中发现连阴雨强度对苹果成熟期的影响小于连阴雨长度,所以仅采用了连阴雨长度的影响因素,没有采用连阴雨强度和温度等影响因素,势必造成了一定的局限性,并有待于在将来的预测实践中不断完善提高。
杜继稳, 等, 2007. 陕西省短期天气预报技术手册[M]. 北京: 气象出版社, 274-283.
|
王景红, 等, 2010. 果树气象服务基础[M]. 北京: 气象出版社, 105-121.
|
陈尚谟, 等, 1988. 果树气象学[M]. 北京: 气象出版社, 225-230.
|
〔苏〕别洛博罗多娃著, 王馥棠译. 提高果树产量的农业气象基础[M]. 北京: 气象出版社, 1985: 9-15.
|
杨振伟, 1996. 苹果生长环境与优质丰产调控技术[M]. 北京: 气象出版社, 109-113.
|
贺皓, 刘宇, 黄宝霞, 2008. 从一次反气旋的生消演变分析陕西初夏连阴雨[J]. 气象, 34(5): 58-63. DOI:10.7519/j.issn.1000-0526.2008.05.010 |
方建刚, 白爱娟, 陶爱玲, 等, 2005. 2003年陕西秋季连阴雨降水特点及环流条件分析[J]. 应用气象学报, 16(4): 509-517. DOI:10.11898/1001-7313.20050412 |
段桂兰, 陶建玲, 郭大梅, 2006. 渭河流域两次秋季连阴雨天气特点对比分析[J]. 陕西气象, (5): 25-28. |
程鹏, 赵庆云, 李江萍, 等, 2007. 西北地区东部一次连阴雨过程等熵位涡分析[J]. 干旱气象, 25(1): 58-62. |
方建刚, 张弘, 白爱娟, 2006. 陕西强连阴雨天气个例的综合分析[J]. 气象科学, 26(5): 578-585. |
胡淑兰, 李社宏, 杜继稳, 2007. 2005年10月秋季连阴雨中暴雨天气特征分析[J]. 陕西气象, (1): 8-11. |
刘光轩, 2005. 中国气象灾害大典(陕西卷)[M]. 北京: 气象出版社, 1-211.
|
陈云峰, 高歌, 2010. 近20年我国气象灾害损失的初步分析[J]. 气象, 36(2): 76-80. DOI:10.7519/j.issn.1000-0526.2010.02.011 |
刘璐, 李艳丽, 2010. 陕西苹果基地县9—10月连阴雨气候特征分析[J]. 陕西气象, (6): 18-20. |
刘璐, 栗珂, 柴芊, 2010. 陕西果业基地县伏旱指数及其预报方法[J]. 气象科学, 30(3): 382-386. |
董晓萌, 罗凤娟, 郭满才, 2007. 时间序列的自回归模型在杨凌地区降水量预报中的应用[J]. 中国农学通报, 23(11): 403-407. DOI:10.3969/j.issn.1000-6850.2007.11.086 |
谌志刚, 王婷, 汪瑛, 等, 2011. 广东省后汛期强对流天气潜势预报方法研究[J]. 气象, 37(8): 936-942. DOI:10.7519/j.issn.1000-0526.2011.08.004 |
金菊良, 杨晓华, 金保明, 等, 2001. 遗传门限自回归模型在气象时间序列预测中的应用[J]. 热带气象学报, 11(4): 415-422. |
穆穆, 陈博宇, 周菲凡, 等, 2011. 气象预报的方法与不确定性[J]. 气象, 37(1): 1-13. DOI:10.11676/qxxb2011.001 |
谷湘潜, 康红文, 江剑民, 2007. 用复数自回归模式预报月平均气温[J]. 应用气象学报, 18(4): 435-441. DOI:10.11898/1001-7313.20070403 |
 2012, Vol. 38
2012, Vol. 38 