2. 成都信息工程学院,成都 610225
2. Chengdu University of Information Technology, Chengdu 610225
随着全球气候变暖,气候要素序列的均一性检验愈来愈受到科学家的关注[1-5]。所谓均一性序列,是指测站得到的气象记录序列仅仅是气候实际变化的反映[6]。然而大多数气候要素序列都受到非气候因素的影响,包括台站迁移、仪器变更和台站环境改变等[7]。利用这些非均一性气候序列分析气候变化,可能导致非真实结论,进而影响气候研究以及业务工作的开展。
国外均一性研究起步较早。自Mitchell在1966年首次提出均一性检验后,Alexandersson等[8]、Solow[9]、Lund等[10]相继发展了SNHT、TPR、Potter等均一性检验方法,并用于北美和欧洲气候数据处理。Slonosky等[11]和Wijingard等[12]利用Buishand、Pettitt、von Neumann方法检验ECA日平均气温、降水和气压数据的均一性。国内,气象资料的均一性检验和订正工作也逐渐受到学者的关注,刘小宁[13-14]、田红[15]、吴利红[16]和宋超辉等[17]总结了气候资料序列的均一性检验方法,并应用于我国部分台站气温和降水序列。李庆祥等[18]、李庆祥[19]和高理[20]利用多种方法对中国东南部地区气候序列进行了均一性检验,力求减少对台站沿革数据的依赖。
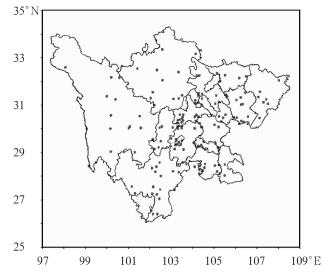
以往均一性检验主要集中在我国东部地区,对西南区域气候资料研究较少。四川省位于中国西南部,地形复杂多样。根据地形特点,本文将四川省气象台站分为盆地底部地区(99个),盆地边缘和川西南山地区(14个),川西北高原区(47个)(见图 1),利用SNHT、TPR、Buishand、Pettitt、MASH和von Neumann法对年平均气温序列进行均一性检验,对比检验结果,分析造成非均一性的可能原因,为气候基本资料的衔接和质量控制工作提供参考依据。
|
图 1 四川省台站分布图 Fig. 1 Station distribution in Sichuan Province |
考虑到四川省1960年以来气温资料的相对完整性,本文从160个台站1960—2009年气温资料中,选取具有连续观测记录50年以上的站点105个。以周边台站为参考站,选相关系数最高的5个台站为待检站,利用比值法构造参考序列Yi。依据Wijingaard等[12]所设定均一性检验思路:通过不同统计方法判断序列的均一性:4种及4种以上方法检验均通过的台站资料为可用,2种不通过的为可疑,至少3种不通过的为不可信。
1.2 方法介绍本文选取SNHT、TPR、Buishand、Pettitt、MASH[21]和von Neumann法对年平均气温序列进行均一性检验。各方法原理在文献[8-12]中已有详细介绍。本文总结各方法具体差异,见表 1。
|
|
表 1 各种检验方法对比 Table 1 Comparison of various test methods |
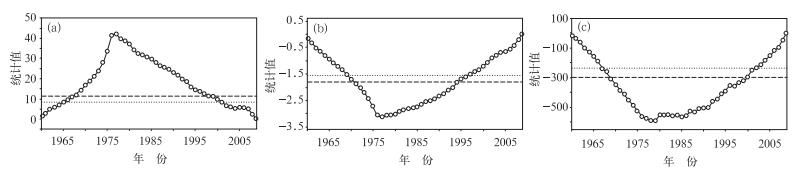
以汶川站(56183) 为例,6种方法均以α=0.01显著性水平下的临界值检验。图 2为汶川站年平均气温采用SNHT、Buishand和Pettitt法的检验结果。图 3为采用TPR法的检验结果;图 4为MASH软件检验汶川站平均气温构建差异序列的检验结果(von Neumann法为非定位检验法,不能给出断点所在年份,因此无检验图)。
|
图 2 汶川站SNHT(a)、Buishand检验(b)和Pettitt检验(c)方法年平均气温的均一性检验图(虚线为α=0.01显著性水平检验,点线为α=0.05显著性水平检验) Fig. 2 The average temperature of Wenchuan Station in the homogeneity test chart by using SNHT (a), Buishand range test (b), and Pettitt test (c) (Dashed line is the 1% significance level, dotted lines for the 5% significance level) |
|
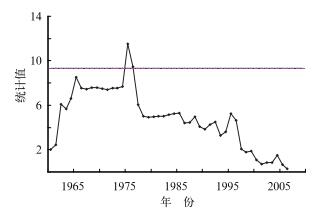
图 3 汶川站TPR方法平均气温的均一性检验图(虚线为α=0.01显著性水平检验) Fig. 3 The average temperature of Wenchuan Station in the homogeneity test chart by using TPR test (Dashed line is the 1% significance level) |
|
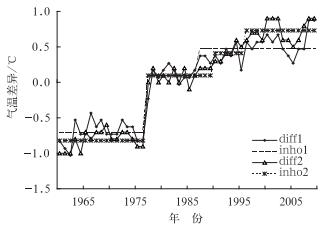
图 4 MASH检验汶川站平均气温差异序列及其转折值 Fig. 4 The difference series and the shift values identified by MASH for the average temperature of Wenchuan Station |
由图 2和3可知,SNHT、Buishand、Pettitt和TPR法计算出的统计量均未通过α=0.01显著性水平检验。由图 4及MASH软件运行结果可明显得出在1976和1986年汶川站存在断点和转折。von Neumann比率法计算出统计量为0.201( < 1.36) 为均一,6种方法中有5种均检验出该序列存在断点,初步判断汶川站气温序列不均一,断点在1977年处。
根据台站沿革资料,1977年7月1日,该站由威州镇姜维城“山腰”迁至汶川县城南部边缘处。图 2和3中,统计序列的最大值均出现在1977年附近,很可能受1977年迁站影响,而图 4中差异序列1和2均在1976和1986年处出现转折,由于MASH软件在检验时自动在均一性程序中给予考虑,并优先考虑元数据,元数据质量在程序中可被检验并通过检验统计量来验证。而在元数据中未被记录但被所有方法检测出来的断点,可能与台站周边大中型建筑(如建筑物抬升)有关(如1986年处的转折),因此元数据不能作为评判气候数据不均一性的唯一完备基础。在以上综合分析基础上,可判断汶川站气温资料具有不均一性。同理,选取不同地形条件下12个代表站,分析检验结果见表 2。
|
|
表 2 12个台站不同方法间断序列的统计 Table 2 The statistics of discontinuous series under different methods in 12 stations |
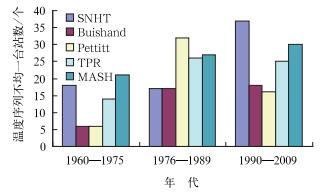
文中所选6种方法均要求原假设为独立、同分布,但拒绝假设存在差异:SNHT、Buishand、Pettitt和TPR法假设在平均值上存在逐步转变(即断点),MASH检验中最优差异序列的统计量通过Monte Carlo法与临界值相比来确定断点位置,这5种方法检验时可定位断点所在年,为特定位置检验法。von Neumann法在拒绝假设中设定该序列非随机分布,因此无法给出断点所在年份的信息。此外,SNHT和Buishand法均假设Yi值为正态分布,但Pettitt法无此限制,它基于序列中要素的排列方式,并非值本身。Pettitt法的排列方式使其对“离群点”的敏感度减弱。TPR法将断点时间作为不可知参数处理,避免data-dredging[9]。为进一步说明特定位置检验法对断点敏感度的区别,现将检验结果去掉突变点位于序列前后两年的站点(虚假不连续点)后分年代统计(见图 5),发现SNHT和TPR法易在序列前端和后端检测断点,Pettitt法对序列中部断点较敏感,这与Wijingard等[12]的研究结论相符。
|
图 5 不同方法检验温度序列断点敏感度 Fig. 5 The breakpoint sensitivity testing of temperature series in different methods |
为了表征检验结果的相似性,借鉴吴利红[16]的“相符率”概念,相符率=检验结果相同站数/被检验站总数。对温度检验结果相符率分析(见表 3),其中SNHT与Buishand法有72个测站的检验结果相同,Pettitt与Buishand法有73个测站的检验结果相同;3种方法中SNHT、Buishand和Pettitt法检验结果相同的台站有51个,相符率为48.6%。可见这3种相关性较好,检验结果最为相似。MASH法假设所有序列都可能存在非均一性变点,通过相同气候区域各站多重比较进行统一检测,对序列的不均一断点及转折点判断较敏感。相较于以上4种方法需要建立参考序列,TPR法则不涉及邻近站是否均一的问题,各台站可以利用该法,独立对自身序列进行均一性检验判断。因此TPR法与其他方法相关性较弱,在综合判断时具有补充作用。
|
|
表 3 温度均一性检验结果相符率(单位:%) Table 3 Matching rate of temperature homogeneity test results (unit: %) |
由四川省105个站点气温序列的检验结果(见表 4),初步判断73个站点可能存在断点,结合台站沿革数据发现43个可疑台站序列中,有12个台站可由迁站或仪器变更信息确定非均一性;其余31个断点因无法确定是人为因素造成,而不作为非均一性断点。综上,四川省年平均气温序列通过均一性检验的台站有32个,占30.5%;可疑台站有31个,占29.5%;非均一的有42个,占40.0%(见图 6)。
|
|
表 4 四川省年平均气温序列均一性检验结果 Table 4 Homogeneity test results of temperature sequence in Sichuan Province |

|
图 6 四川省气温序列通过均一性检验(实心点)和未通过均一性检验(空心点)台站分布图 Fig. 6 Station distribution of the temperature series in Sichuan Province which passed the homogeneity test (dark dots) and not (circles) |
分测站类型进行温度均一性检验时发现,基准站有5个,无不均一台站;基本站24个,均一占20.8%;一般站76个,均一台站占28.9%。由于四川地形变化明显,气候资料代表的区域范围较为有限。因此,大范围的气候变化研究宜选择代表性范围尽可能大的站点。
借鉴吴利红[16]对断点原因的分类,本文将非均一性原因作如下定义:间断点与测站迁站时间基本吻合(允许误差5年)为迁站原因;由于仪器重新安置而导致资料序列的非均一性为仪器变化原因;其他无明显环境破坏记载,定义为不明原因。联系台站沿革数据,将非均一性台站分类,见表 5。统计发现,迁站对气温序列均一性检验影响很大。在160个测站中,1960—2009年有111个台站有迁站史(占检测站总数的69.4%),检验因迁站引起的非均一性有44个,其中有33个站(75%)的“地理环境”变化剧烈,如在“郊区”和“市区”间迁移,以及迁站前后地理环境受城市化影响,由郊区变为“市区”。在迁站后仍为均一的台站中,有10个台站迁移前后地理环境相同,如从“郊区”迁移到“郊区”。分年代统计,20世纪60—70、80—90年代以及2000年以后不均一台站有增加的趋势,其中60—70和80—90年代不均一性均由台站迁移所致,2000年后台站不均一性90%为仪器的变更造成的。
|
|
表 5 四川省年平均气温序列非均一性原因统计 Table 5 The causes for inhomogenization on the temperature sequence |
由于地理条件的差异,各台站对检验方法的适用性也不同,以降低误判断点为前提,利用台站沿革数据验证各方法所得断点的真实性(见表 6),在显著水平为0.01时,6种方法显露年数占总年数的百分比分别是:SNHT法为59.4%,Buinshand法为33.3%,Pettitt法为37.1%,von Neumann法为49.5%,TPR法为73.3%,MASH为55.2%。可见TPR检验法对非均一性断点最敏感,SNHT和MASH法次之,其中MASH法检验为增加统计检验的效率,由差异序列的最小方差决定最优权重,假设待检序列就是所有的差异序列中唯一的普通序列,在所有差异序列中检测到的断点就认为是待检序列中的断点,多样性检验程序基于通过一个显著性水平的假设检验,并且要同时考虑第一类误差(虚假和多余不均一性的检验)以及第二类误差(真实不均一性的忽略)。因此对断点及转折的判断也较为敏感。综合分析各检验方法,发现3种或3种以上同时显露的间断点占32.4%,两种或两种以上同时显露的间断点占74.3%,表明两种方法在大多数情况下都能显露出相同的间断年份,因此应用这些方法检验温度序列非均一性是较为有效的。进一步联系台站沿革数据分析不同地形下各种方法检验效果,以SNHT法为例(见表 7),检测出的显露年份可由元数据解释的台站数中盆地占67.6%,误判为17.6%;山地显露率占57.1%,误判为28.6%;高原显露率占57.1%,误判占14.3%。
|
|
表 6 不同地形各方法判断气温间断的统计 Table 6 The statistics of different methods to determine the breakpoint of temperature in different regions |
|
|
表 7 不同地形下SNHT法对温度均一性检验 Table 7 SNHT to determine the breakpoint of temperature in different regions |
同理对SNHT、Buishand、Pettitt、TPR及MASH法进行比较,并参考各台站具体数据(见表 8),分析发现Buishand法的显露年份大部分与SNHT法所显露的年份相同,检验盆地及山地台站时,SNHT法显露率最高,分别为67.6%和57.1%,漏检和误判较少;高原地区SNHT和Buishand法显露率较高,分别为57.1%和50%,Buishand法漏检和误判率最低。因此,对于盆地和川西南山地台站,SNHT法判断的气温序列断点与实际较符合;川西北高原台站,Buishand法适用性较强。
|
|
表 8 温度均一性检验各方法漏检和误判率(单位:%) Table 8 The missed rate and false positives of temperature in different regions with different methods (unit: %) |
(1) 在显著性水平α=0.01的检验中,四川省105个待检台站年平均气温序列通过均一性检验的有32个,占30.5%;其中均一的基准站有5个,基本站有5个,一般站有22个。均一的基本站和一般站的使用将扩展气候资料代表的区域范围,提高气候资料的使用率,有助于四川省的气候变化研究。
(2) 可疑台站有31个,占29.5%;造成这类台站无法确定断点的原因,一方面可能由其他因素产生,如气候变化、环境变化、观测方法改变等原因,需要进一步分析;另一方面可能由于台站沿革资料不完备造成,致使断点信息无法查阅。因此对于不明原因的断点序列,必须通过更加详细的历史沿革资料判断其真实性。
(3) 不均一台站42个,占40%,利用这部分温度资料序列进行气候气候变化分析研究时应注意资料的订正。
4.2 非均一性原因序列不均一原因中,因迁站导致的有28个,更换仪器引起的有18个。分年代统计,20世纪60—70、80—90年代以及2000年以后不均一台站有增加的趋势,其中60—70和80—90年代不均一性均由台站迁移所致。再次证实,迁站是引起序列间断的主要原因之一。
4.3 检验方法评估分析对不同方法的敏感度和适用性作评估分析发现,SNHT和TPR法易在序列前端和后端检测断点,Pettitt法对序列中部断点较敏感,MASH对序列各部断点检测均较敏感,这与其差异序列的数学原理及检验效率有关。SNHT与Buishand和Pettitt法检验结果相符率为48.6%,TPR法与其他方法相符率偏低,但该法不涉及邻近站是否均一,因此检验中可做补充判断。根据四川省特殊地形分析,发现对盆地及山地台站而言,SNHT法显露率最高,分别为67.6%和57.1%,漏检和误判较少;高原地区SNHT法和Buishand法显露率较高,其中Buishand法漏检和误判率最低。
因此,鉴于减小对元数据依赖度的均一化检验思路,在缺乏元数据时,应采用多种检验方法综合分析,有助于气候资料在区域气候变化研究中的有效利用。
致谢:上海台风研究所陈葆德老师、占瑞芬老师,中科院大气所李珍老师以及四川省气候中心孙昭萱、钟燕川同志对本工作给予很多指点和帮助,谨致谢忱。
李庆祥, 刘小宁, 张洪政, 等, 1999. 定点观测气候序列的均一性研究[J]. 气象科技, 31(1): 3-10. |
曹丽娟, 鞠晓慧, 刘小宁, 2010. PMFT方法对我国年平均风速的均一性检验[J]. 气象, 36(10): 52-56. DOI:10.7519/j.issn.1000-0526.2010.10.008 |
曾红玲, 张强, 祝昌汉, 2010. 三峡库区气压资料的不均一性检验及订正[J]. 气象, 36(10): 57-61. DOI:10.7519/j.issn.1000-0526.2010.10.009 |
张智, 林莉, 梁培, 等, 2009. 宁夏年气温资料的均一性检验研究[J]. 气象, 35(10): 79-83. DOI:10.7519/j.issn.1000-0526.2009.10.009 |
王秋香, 李庆祥, 周昊楠, 等. 中国降水系列均一性研究及对比分析[J]. 气象, 待发表.
|
Standt M, Esteban Parra M J, Castro-Diez Y, 2007. Homogenization of long-term monthly Spanish temperature data[J]. International J Climate, 27(13): 1809-1823. DOI:10.1002/(ISSN)1097-0088 |
吴增样, 2005. 气象台站历史沿革信息及其对观测资料序列均一性影响的初步分析[J]. 应用气象学报, 10(4): 461-467. DOI:10.11898/1001-7313.20050406 |
Alexandersson H, Moberg A, 1997. Homogenization of Swedish temperature data. Part I: Homogeneity test for linear trends[J]. J Climatol, 17(1): 25-34. DOI:10.1002/(ISSN)1097-0088 |
Solow A R, 1987. Testing for Climate Change: An application of the two-phase regression model[J]. J of Climate and Applied Meteorology, 26(10): 1401-1405. DOI:10.1175/1520-0450(1987)026<1401:TFCCAA>2.0.CO;2 |
Lund R, Reeves J, 2002. Detection of undocumented changepoints:A revision of the two-phase regression model[J]. J Climate, 15(17): 2547-2554. DOI:10.1175/1520-0442(2002)015<2547:DOUCAR>2.0.CO;2 |
Slonosky V, Jones P D, Davies T D, 1999. Homogenization techniques for European monthly mean surface pressure series[J]. J Climate, 12(8): 2658-2672. DOI:10.1175/1520-0442(1999)012<2658:HTFEMM>2.0.CO;2 |
Wijingaard J B, Klein Tank A M G, Können G P, 2003. Homogeneity of the 20th century European daily temperature and precipitation series[J]. International Journal of Climatology, 23(6): 679-692. DOI:10.1002/joc.v23:6 |
刘小宁, 2000. 我国40年年平均风速的均一性检验[J]. 应用气象学报, 11(1): 27-34. |
刘小宁, 1995. 年降水量序列非均一性检验方法探讨[J]. 气象, 21(8): 3-8. DOI:10.7519/j.issn.1000-0526.1995.08.001 |
田红, 2008. 江淮流域年降水量和气温的均一性检验[J]. 气象科学, 28(2): 227-231. |
吴利红, 2007. SNHT方法用于气温序列非均一性检验的研究[J]. 科技通报, 23(3): 338-341. |
宋超辉, 刘小宁, 李集明, 1995. 气温序列非均一性检验方法的研究[J]. 应用气象学报, 6(3): 289-296. |
李庆祥, 江志红, 2008. 长江三角洲地区降水资料的均一性检验与订正试验[J]. 应用气象学报, 19(2): 220-225. |
李庆祥, 2005. 利用多模式对中国气温序列中不连续点的检测[J]. 气候与环境研究, 10(4): 736-742. |
高理, 2010. 山东省观测资料的均一性检验[J]. 山东气象, 30(121): 1-4. |
Li Zhen, Yan Zhongwei, 2010. Application of multiple analysis of series for homogenization to Beijing daily temperature serises (1960—2006)[J]. Adv Atmos Sci, 27(4): 777-787. DOI:10.1007/s00376-009-9052-0 |
 2012, Vol. 38
2012, Vol. 38 
