引言

天气预报存在着不可避免的不确定性(Lorenz, 1963; 1965), 概率是表达预报不确定性的一种方式(王东海等，2011)，集合预报(杜钧等，2010；矫梅燕，2010；陈静等，2002)则是获得概率预报的一个有效途径。集合预报产品的释用是集合预报系统必不可少的一部分，是实现模式结果实际应用价值的重要过程。目前的集合预报释用方法主要以模式预报值为样本，统计得到一系列概率预报结果，如天气要素概率预报图、邮票图和面条图等。由于集合预报系统在获得不确定性来源过程中仍存在一定缺陷，由此得到的直接概率预报结果并不能完整地定量化表达不确定性，因此，近年来国内外气象学者逐渐研究基于贝叶斯理论的概率预报方法来解决这一问题。

贝叶斯理论是统计学中的一个重要分支，在水文预报及气象预报等领域有所应用。从20世纪90年代开始，基于贝叶斯理论的水文模拟不确定性估计方法被广泛地应用于模拟方法、参数估计和水文预报等方面，成为水文不确定性研究的主流方向。90年代末，气象学者将贝叶斯理论应用于单一数值预报产品的概率化预报中，如Krzysztofowicz(1983；1999a)提出了贝叶斯产品处理技术(Bayesian Processor of output, BPO)，采用模式预报值作为预报因子，通过建立BPO预报模型对预报量先验概率修订，得到预报量累积概率分布或概率密度的预报。随着数值预报技术的发展，集合预报逐渐发展成熟，近年来贝叶斯理论也逐渐应用于该研究领域，Raftery(2005)提出了贝叶斯模式平均(Bayesian Model Averaging，BMA)的方法，利用地面温度历史集合预报资料，将单个集合成员预报结果修订为概率密度函数形式的预报, 但由于模式集合平均与气候平均有很大差别，该方法对于极端事件的预报不够准确。Bishop(2008)对上述方法进一步地改进，将气候分布与贝叶斯理论结合得到既适用于非极端事件又适于极端事件的概率预报。中国气象局也于2010年开始这方面的研究，赵琳娜等(2011)采用淮河流域历史降水资料及集合预报资料利用BMA方法对中国气象局(CMA)集合预报15个成员的定量降水预报进行了集成与订正，得到有预测效果的概率密度函数，使得观测降水真值包含在有效区间预报内的可能性更大，获得预报能力高于确定预报的概率预报。陈法敬等(2011)以连续预报量—温度为例，对BPO方法在集合预报中的应用进行了初步试验验证，将一组集合成员预报值修订为一组概率预报并对其预报结果合理融合得到预报能力高于单一集合成员的集成贝叶斯概率预报。

由前人基于贝叶斯理论的概率预报结果可以看出，采用数值模式产品提供的有效预报信息对预报量的气候(先验)概率进行修订，得到模式预报信息与气候信息最佳融合的概率预报可以提高预报准确性。降水作为离散型预报量，其概率预报形式一般有两种：降水有无的分类概率预报和降水量等级概率预报。实际上，降水量在[0, ∞)内的各个连续值处都存在一定概率，获得该范围内连续的概率分布或概率密度预报可以更加完整地体现预报不确定性。本文以24小时降水为预报量，集合成员预报值为确定预报值，根据BPO方法(Krzysztofowicz et al, 2001; Krzysztofowicz, 1999)建立降水概率预报模型，获得一组在预报范围内连续变化的降水概率分布或概率密度预报，并按照预报能力对各集合成员贝叶斯降水概率预报信息融合，获得集成贝叶斯降水概率预报。

1 方法和资料 1.1 方法 1.1.1 贝叶斯方法

贝叶斯方法是基于贝叶斯定理而发展起来用于系统地阐述和解决统计问题的方法(茆诗松，1999；吴喜之，2000)。该方法的核心为贝叶斯公式，其基本形式如下：

$ {P}{\rm{(}}{Y}{\rm{|}}{X}{\rm{) = }}\frac{{{P}{\rm{(}}{Y}{\rm{)}}{P}{\rm{(}}{X}{\rm{|}}{Y}{\rm{)}}}}{{{P}{\rm{(}}{X}{\rm{)}}}} $

(1)

式中，P(Y)是未知数Y的先验概率，它是由已知的先验信息获取的最初概率，反映了人们在抽样前对Y的认知；P(X|Y)则是样本值X的抽样分布密度, 其综合了未知数Y的样本信息和总体信息(综合称为抽样信息)；P(X)为随机变量X的边缘分布。公式表达了通过抽取样本X，利用抽样信息对未知数Y的先验概率进行修订，得到重新估计的条件概率即后验概率P(Y|X)的算法。

1.1.2 BPO方法

BPO方法是一种将贝叶斯理论运用到气象领域，通过融合预报量先验信息，将单一数值模式预报值修订为概率预报的技术。本文选取降水作为预报量Y，将单一集合成员降水预报值作为预报因子X。由于离散型预报量降水总体上可以分为有无降水两种情况，而在有降水条件下的降水量(以下简称为条件降水量)的分布在(0, ∞)范围内是连续的。因此为了得到降水在[0, ∞)预报值范围内连续的概率分布预报，分别对有降水的概率和条件降水量的概率分布修订，得到有降水的后验概率π及条件降水量的后验概率分布Φ(y)或后验密度函数ϕ(y)。基于BPO方法的降水概率预报数学模型如式(2) 或(3) 所示，式中x为预报因子X的值，y为≥0的任意实数，δ(y)为y的狄拉克函数。由公式可以看出，基于BPO方法得到的降水概率预报由两部分构成：无降水的概率和条件降水量的概率分布。

概率分布形式：

$ P\left( {Y \le y|X = x} \right) = \left( {1 - \pi } \right) + \pi \mathit{\Phi }\left( y \right),y \ge 0 $

(2)

概率密度形式：

$ P\left( {y|X = x} \right) = \left( {1 - \pi } \right)\delta \left( y \right) + \pi \phi \left( y \right),y \ge 0 $

(3)

降水概率预报模型中有降水的后验概率π由公式(4) 获得，式中g为由历史降水观测资料统计得到的有降水先验概率(降水阈值为0.1 mm)。f₀、f₁则分别为无降水和有降水时，由降水观测值、预报值构成的联合样本获得的预报值x的条件密度函数即似然函数。

$ \pi = {\left[ {1 + \frac{{1 - g}}{g}\frac{{{f_0}\left(x \right)}}{{{f_1}\left(x \right)}}} \right]^{ - 1}} $

(4)

模型中条件降水量的后验概率分布Φ(y)和后验概率密度ϕ(y)则分别由式(5) 和(6) 获得。公式中Q代表标准正态分布函数；G(y)、K(x)则是分别由降水历史观测值样本、预报值样本估计得到的条件降水量y的先验概率分布、预报值x的边缘分布；c₀、c₁和T为通过建立似然模型得到的后验参数。

概率分布函数形式：

$ \mathit{\Phi }\left(y \right) = Q\left\{ {\frac{1}{T}\left[ {{Q^{ - 1}}G\left(y \right) - {c_1}{Q^{ - 1}}K\left(x \right) - {c_0}} \right]} \right\} $

(5)

概率密度函数形式：

$ \begin{array}{l} \phi \left(y \right) = \frac{1}{T}\exp \left({\frac{1}{2}\left\{ {{{\left[ {{Q^{ - 1}}G\left(y \right)} \right]}^2} - } \right.} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\left. {\left. {{{\left[ {{Q^{ - 1}}\mathit{\Phi }\left(y \right)} \right]}^2}} \right\}} \right)g\left(y \right) \end{array} $

(6)

似然模型是为了获得表征预报量和预报因子之间依赖关系的似然参数而建立的数学模型。由于降水观测值与预报值并不服从标准正态分布，其分布特征使得两者之间的依赖关系难以用解析函数来刻画，因此本文采用Kelly等(1997)和Krzysztofowicz(1997)提出的亚高斯似然模型来获得似然参数。其主要思想是先通过正态分位数转换(Normal Quantile Transform, NQT)将预报量y、预报因子x变换为正态分布变量u、z，如式(7)。

$ u = {Q^{ - 1}}G\left(y \right), z = {Q^{ - 1}}K\left(x \right) $

(7)

式中，Q^-1表示标准正态分布函数反函数，因此转换后的变量均完全服从标准正态分布(高斯分布)。在转换空间内建立的似然模型则为亚高斯似然模型，根据u、z的均值μ₀、μ₁, 方差σ₀²、σ₁²以及协方差σ₁₀通过式(8) 得到似然参数a、b和σ²，以此来描述NQT转换量u、z之间的线性回归关系，如式(9) 所示。

$ a = \frac{{{\sigma _{10}}}}{{\sigma _0^2}},b = {\mathit{\mu }_1} - \frac{{{\sigma _{10}}}}{{\sigma _0^2}}{\mathit{\mu }_0},{\sigma ^2} = \sigma _1^2 - \frac{{\sigma _{10}^2}}{{\sigma _0^2}} $

(8)

$ E\left( {Z|U = u} \right) = au + b,Var\left( {Z|U = u} \right) = {\sigma ^2} $

(9)

式中，E为降水观测值Y的NQT转换量U值为u时，预报值X的转换量z的期望，Var则为其方差。同时，通过建立似然模型分别由式(10) 和(11)，获得表征预报因子有效信息评价指标的有效信息评分(Informativeness Score, IS)(Krzysztofowicz, 1992)及BPO预报模型中的后验参数。

$ IS = \left| \gamma \right| = {\left[ {{{\left({\frac{a}{\sigma }} \right)}^{ - 2}} + 1} \right]^{ - \frac{1}{2}}} $

(10)

$ {c_1} = \frac{a}{{{a^2} + {\sigma ^2}}}, {c_0} = \frac{{ - ab}}{{{a^2} + {\sigma ^2}}}, T = {\left({\frac{{{\sigma ^2}}}{{{a^2} + {\sigma ^2}}}} \right)^{1/2}} $

(11)

1.2 资料

本文选取了5个不同气候区的代表站点:广州、南京、武汉、成都和北京站。将站点24 h降水量作为预报量Y，集合预报系统中单一集合成员24 h降水预报值(预报时效为24、72和120 h)作为预报因子X。

其中降水的先验概率由国家气象信息中心提供的全国基准站1952—2007年6月逐日20—20时24 h降水观测资料获得。为了研究BPO方法在多模式集合预报中的应用，本文预报因子X是由交互式全球大集合预报系统(THORPEX Interactive Grand Global Ensemble，TIGGE)提供的中国气象局(CMA)与美国环境预报中心(NCEP)逐日24、72和120 h预报时效的全球格点降水预报资料利用双线性插值方法得到广州、南京、武汉、成都和北京站5个观测站的降水预报，试验时段为2008年6月1—30日期间。

2 基于确定性预报的降水概率预报模型试验 2.1 降水概率预报模型的应用实例

以CMA和NCEP集合预报资料中集合控制预报值作为确定性预报值，对基于BPO方法的降水概率预报模型进行应用试验。

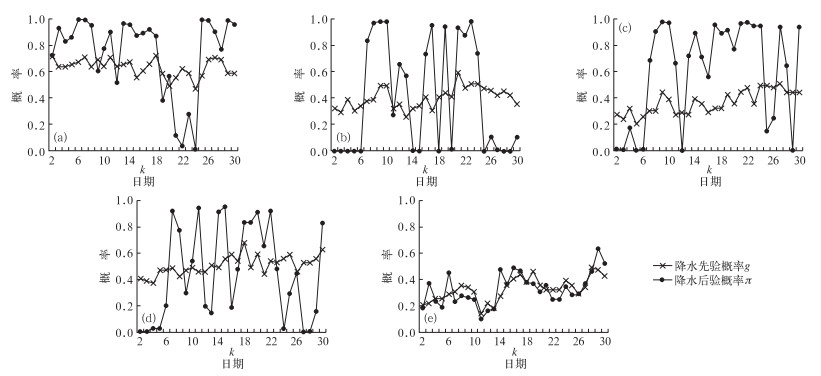
分别对广州、南京、武汉、成都和北京站建立BPO降水概率预报模型，得到5个站点的6月逐日有降水的后验概率π_k，其与历史观测资料统计得到的先验概率g_k比较结果如图 1所示(k为6月中的第k天)。

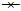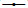由图 1可以看出，根据降水历史观测资料统计得到的站点有降水先验概率g_k逐日变化平缓，其中广州站的g_k值在0.45~0.75之间(如图 1a)，武汉和成都站的g_k值在0.3~0.7之间(如图 1b和1d), 南京和北京站的g_k值在0.2~0.5之间(如图 1c和1e)。而通过建立BPO降水概率预报模型修订得到的后验概率π_k逐日变化起伏较大，这说明数值预报值作为预报因子，提供的预报因子有效信息发挥了一定修订作用。

将历史观测资料中有降水时的降水观测值作为条件降水量的历史观测样本，与其对应的集合预报控制预报值作为历史预报值样本，通过统计分析发现广州、南京、武汉、成都和北京站的6月逐日条件降水量近似服从威布尔分布。因此，本文采用威布尔分布函数估计条件降水量的先验分布G(y)和预报值的边缘分布K(x)。

$ G\left({y\left| {\alpha, \beta } \right.} \right) = 1 - {{\rm{e}}^{ - {{\left({\frac{y}{\alpha }} \right)}^\beta }}}, y > 0 $

(12)

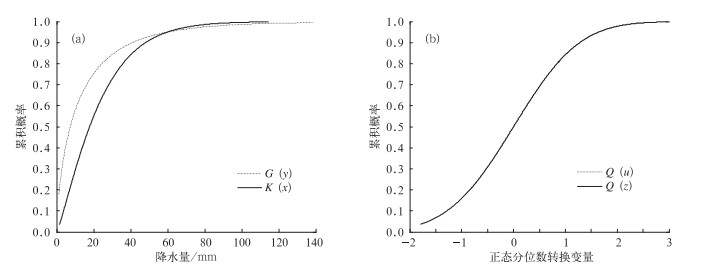
以广州站2008年6月29日为例，条件降水量的先验分布G(y)及预报值边缘分布K(x)如图 2a所示。可以看出，条件降水量Y、预报值X的威布尔分布形状与尺度存在差异，两者之间的统计关系难以统一刻画。分别对其进行NQT转换，得到条件降水量、预报值的NQT转换量U、Z，其分布形式如图 2b所示。转换量U、Z均服从标准正态分布，分布曲线完全重合，便于似然模型的建立。

以CMA和NCEP集合预报为例，在转换空间内分别建立5个研究站点的似然模型，得到后验参数c₀、c₁和T, 结果如表 1和表 2所示。

利用表 1中广州站的后验参数值，由式(6) 得到给定任意4个预报因子值(X=10、20、35和55 mm)时的条件降水量后验概率密度函数，如图 3所示。

由图 3可见，预报因子值分别取10、20、35和55 mm时，概率密度峰值对应的降水量分别为1、5、15和35 mm。同时，先验概率密度G(y)的峰值位于条件降水量小值区(倒J型分布)，而预报因子x值愈大，修订得到的后验密度函数ϕ(y)愈圆滑，峰值也随之向降水量大值区移动，而体现了预报因子对概率的修订作用。

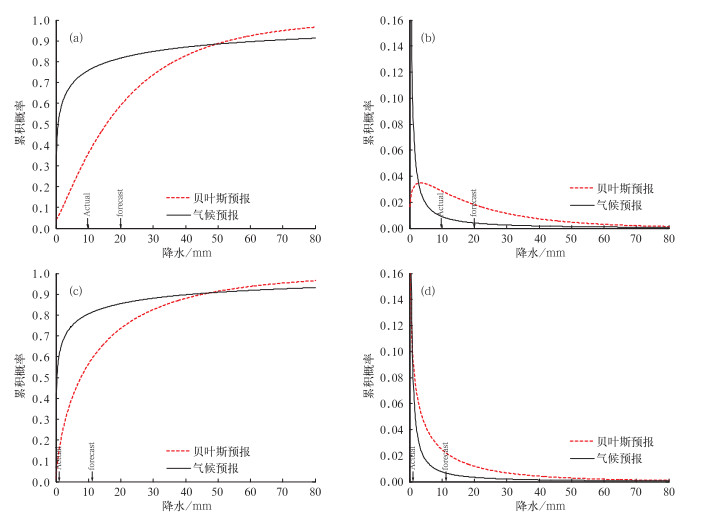
2.2 基于确定性预报的降水概率预报结果分析

分别将CMA和NCEP集合预报控制预报值作为确定性预报，对广州、南京、武汉、成都和北京站2008年6月逐日24 h降水建立BPO降水概率预报模型，得到各站点的逐日降水概率分布或概率密度预报。其中，以CMA控制预报对广州2008年6月30日降水, NCEP控制预报对武汉2008年6月21日降水的预报为例，得到确定性预报的概率化结果—单一集合成员贝叶斯降水概率预报的结果如图 4所示。

由图 4可以看出，广东站的实际观测值为8.9 mm，CMA控制预报结果为19.3 mm, 修订得到的概率密度峰值位于观测值附近(如图 4b)，预报准确性有所提高；武汉站的实际观测值为0.4 mm，NCEP控制预报结果为10.93 mm，修订得到的概率密度峰值同样位于观测值附近(如图 4d)，且预报确定度较高。同时，得到的贝叶斯降水概率预报与确定性预报相比，给出了预报范围内更多的预报信息，并以概率的形式定量化、连续地表达了降水预报不确定性。

本文选取的成都、南京和北京站的试验个例得到的贝叶斯降水概率预报形式与以上广州、武汉站的个例相似，不再赘述。

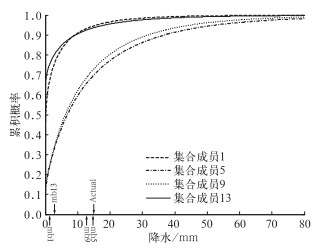
3 基于集合预报的降水概率预报模型应用 3.1 集合成员的预报模型应用结果

前面阐述了基于确定性预报建立BPO降水概率预报模型，获得单一集合成员贝叶斯降水概率预报的方法。试验结果表明，得到的概率预报具有一定的预报能力。而集合预报的预报不确定性是所有集合成员预报不确定性的完整体现，因此有必要研究一种合理的集合成员概率预报信息融合方法。将集合预报结果包含的一组集合成员预报值(x₁, …, x_n)(n为集合成员数)中每个集合成员预报值视为确定预报数值模式产品，基于BPO方法建立降水概率预报模型，获得一组概率分布预报{P(Y≤y|X=x_i)|i=1, …, n}。以广州站2008年6月4日的24小时降水预报为例，图 5给出CMA集合预报第1、5、9和13集合成员贝叶斯降水概率预报。

由图 5可以看出，降水观测值为14.4 mm，选定的CMA集合成员预报值均小于实况。概率化后的集合成员1和集合成员13的贝叶斯降水概率分布预报较相似，集合成员5和集合成员9的概率分布预报结果近乎重合。这表明，集合成员的降水预报值存在差异，所包含的不确定信息不同，因此其概率分布预报也有所区别。

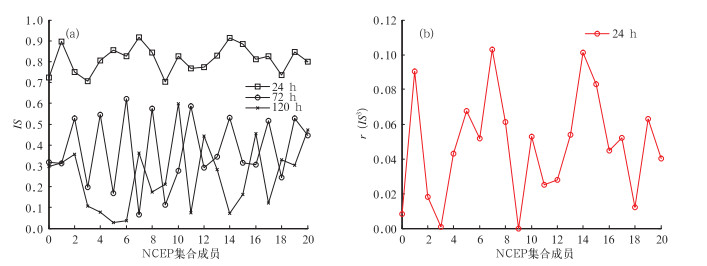
3.2 基于集合成员贝叶斯降水概率预报结果的集成方法

由于集合成员为预报提供的有效预报信息存在差异，其预报能力也有所不同。本文采用在亚高斯似然模型中获得的预报因子有效信息评分IS值表征其预报能力。IS值的范围为[0, 1]，且IS值越大，预报因子包含的有效预报信息越多，集合成员的预报能力越高。分别基于CMA和NCEP集合预报成员对南京站24、72和120 h的降水预报值建立亚高斯似然模型，根据式(10) 得到各集合预报成员的IS值，其中NCEP集合成员的结果如图 6a所示。

由图 6a可见，基于NCEP集合成员24 h降水预报得到的IS值明显高于72和120 h，其中预报能力最强的为集合成员7，预报能力最弱的为集合成员9，IS值分别为0.91和0.70。

IS值可以较好地体现集合成员为预报量提供有效预报信息的能力，因此本文采用正比于IS³的值作为权重系数(陈法敬，2011)来体现不同预报能力的集合成员其预报信息在所有集合成员预报信息融合中的地位，见式(13)。

$ {r_i}\left({I{S_i}} \right) = \frac{{IS_i^3 - \min \left({\mathit{\boldsymbol{I}}{\mathit{\boldsymbol{S}}^3}} \right)}}{{\sum\limits_{i = 1}^n {IS_i^3 - n \cdot \min \left({\mathit{\boldsymbol{I}}{\mathit{\boldsymbol{S}}^3}} \right)} }} $

(13)

式中，min运算为取各集合成员组成的IS³向量中最小的元素，n为集合成员总数。

以NCEP对南京站24 h降水预报为例，获得与图 6a中24 h预报时效的集合成员IS值对应的r_i(IS_i)值，如图 6b所示。

由图 6b可见，权重系数的变化趋势与IS值一致，对于24 h预报能力最强的集合成员7，其预报信息的权重系数r_i(IS_i)值也最大，预报能力最弱的集合成员9，其预报信息的权重系数r_i(IS_i)值最小，r_i(IS_i)值分别为0.11和0。

另外，分别基于CMA和NCEP集合预报对广州、武汉、成都和北京站24、72和120 h降水预报得到集合成员IS值以及24 h降水预报信息的权重系数r_i(IS_i)。结果表明，权重系数可以很好地体现不同预报能力的集合成员其预报信息在融合中的地位。同时，各站的IS值变化特征与南京相似，两个集合预报系统对24 h降水预报能力均明显高于72和120 h预报。

基于权重系数r_i(IS_i)根据式(14) 对一组集合成员概率密度预报信息加权平均且归一化，得到融合后的集成贝叶斯降水概率密度预报。由式(15) 对概率密度函数积分，得到概率分布预报。

$ p\left({y|\mathit{\boldsymbol{X}}} \right)\mathit{\boldsymbol{ = }}\frac{{\sum\limits_{i = 1}^n {p\left({y|{x_i}} \right) \cdot {r_i}\left({I{S_i}} \right)} }}{{\int\limits_0^\infty {\left[ {\sum\limits_{i = 1}^n {p\left({\xi |{x_i}} \right) \cdot {r_i}\left({I{S_i}} \right)} } \right]} {\rm{d}}\mathit{\xi }}} $

(14)

$ p\left({Y \le y|\mathit{\boldsymbol{X}}} \right)\mathit{\boldsymbol{ = }}\int\limits_0^y {p\left({\xi |\mathit{\boldsymbol{X}}} \right)} {\rm{d}}\mathit{\xi } $

(15)

3.3 集成贝叶斯降水概率预报结果分析及检验

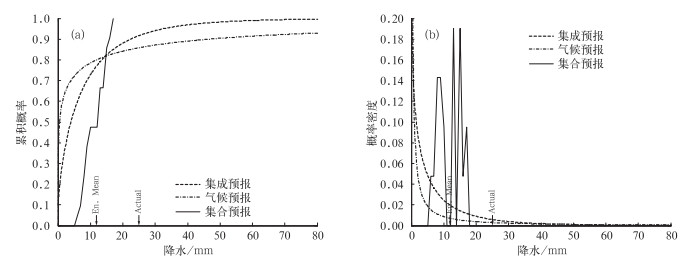
以NCEP对广州2008年6月8日的24 h降水预报为例，分别对各集合预报成员建立BPO降水概率预报模型，获得一组集合成员贝叶斯降水概率预报，并根据式(14) 和(15) 对预报信息融合，得到集成贝叶斯降水概率预报，如图 7所示。

由图 7可以看出，个例的降水观测值为24.8 mm，NCEP集合预报给出的累积概率在此处已达到极值1，概率密度为0。集合模式直接概率预报的概率密度峰值主要位于9、13和15 mm，对应的降水等级范围则为小到中雨。修订得到的集成概率分布和概率密度预报在预报范围内是连续变化的曲线，且降水观测值处的概率密度有所提高，增加了预报的可靠性。

分别基于CMA和NECP集合预报对广州、南京、北京、成都和武汉的2008年6月逐日24 h降水预报，建立BPO降水概率预报模型，得到站点逐日集成贝叶斯降水概率预报。采用连续等级概率评分(Continuous Ranked Probability Score, CRPS)对各站点的概率预报结果进行检验，CRPS值越小说明概率预报可靠性越高，预报结果越接近真实情况。

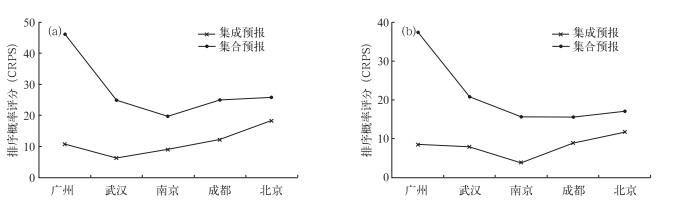
图 8给出了5个站点集成贝叶斯降水概率预报和集合直接概率预报的6月CRPS评分均值，其中图 8a和8b是分别为基于CMA和NCEP集合预报得到的检验结果。

由图 8可以看出，基于CMA和NCEP集合预报得到的广州、武汉、南京、成都和北京站6月集成贝叶斯降水概率预报的CRPS评分均值明显小于集合直接概率预报，即集成贝叶斯降水概率预报的准确性高于集合直接概率预报。同时，各站点的集成预报与集合预报的CRPS评分变化趋势一致，说明得到的集成贝叶斯降水概率预报的预报效果仍基于集合预报结果。其中，基于CMA和NCEP集合预报获得的集成贝叶斯降水概率预报均对广州站的预报准确性改进最大。基于CMA集合预报得到的集成预报结果中，武汉站的CRPS值最小，预报准确性最高，基于NCEP集合预报得到的集成预报结果中，南京站的CRPS值最小，预报准确性最高。

综上所述，分别基于CMA和NCEP集合预报对广州、武汉、南京、成都和北京站的2008年6月逐日24 h降水建立降水概率预报模型并采用CRPS评分检验。结果表明，各站点的集成贝叶斯降水概率预报的可靠性均高于集合直接概率预报，并对广州站的概率预报准确性有较大提高，这种基于贝叶斯理论的集合降水概率预报方法经试验证明是科学合理的。

4 结论

采用1952—2007年历史观测资料、2008年集合预报资料对基于贝叶斯理论的集合降水概率预报方法进行初步应用试验，得到以下结论：

(1) 基于BPO方法对广州、武汉、南京、成都和北京站6月逐日有降水的先验概率g修订得到的后验概率π逐日变化明显，预报值提供的预报因子有效信息发挥了修订作用。

(2) 得到的单一集合成员贝叶斯降水概率预报与确定性预报相比，给出了预报范围内更多的预报信息，并以概率的形式定量化、连续地表达了降水预报的不确定性。

(3) 每个集合成员的预报性能存在差异，以IS值表征集合成员的预报能力，结果表明集合成员预报能力随着预报时效增加而降低。用正比于IS³的值作为权重系数可以有效地体现不同预报能力的集合成员其预报信息在融合集成中的地位。

(4) 采用CRPS方法对5个研究站点的集成贝叶斯降水概率预报和集合直接概率预报检验，结果表明，基于BPO方法得到的集成预报可靠性高于集合预报，并对广州站的概率预报准确性有较大提高，该降水概率预报方法具有合理性。

文中采用双线性插值的方法由格点集合预报资料得到站点降水预报值，存在一定误差，对试验结果略有影响；试验样本长度仅为1个月，较小的样本量可能导致存在较大的预报模型偏差，其结果的代表性不是很强。另外值得注意的是，本文根据历史观测资料，采用威布尔分布估计得到的气候分布作为先验信息，其方法及结果存在一定局限性。由于先验信息的获取有多种途径，因此还可以尝试其他先验信息的估计方法，并与本文所得结果做进一步对比。下一步的工作将针对上述缺陷进行改进，对基于贝叶斯理论的集合降水概率预报方法进一步深入研究。