2. 国家气象中心,北京 100081;
3. 新疆维吾尔自治区气象台,乌鲁木齐 830002
2. National Meteorological Centre, Beijing 100081;
3. Meteorological Observatory of Xinjiang Uygur Autonomous Region, Urumqi 830002
云是表征天气气候特点的重要因素之一,也是大气动力、热力和水分输送过程综合作用的外在表现,在地球系统的能量平衡中起着重要的作用(章建成等,2006)。云量和云结构变化又是一个反映地-气相互作用强的参数(徐兴奎,2012),云的种类、尺度、结构特征及其演变严重影响着大气辐射,从而影响着大气温度的变化。因此在模式中对云量的准确模拟具有重要的意义。关于云量参数化方面的已有工作,主要有诊断方案、预报方案、统计方案和统计-动力预报方案等。云量诊断方案的代表是Slingo(1987)的工作,云量预报方案中的代表是Tiedtke(1993)的工作,云量统计方案的代表性工作为Sommeria(1977),而统计-动力预报方案的代表性工作为Tompkins(2002)。这些工作对大气模式中的云量问题进行了多方面的探索,就方法而言,诊断方案和预报方案是一种决定性的方法,而统计方案事实上是概率论方法,统计-动力预报方案是这两种方法的混合方案。由于决定云的过程小至分子尺度的核化作用尺度,大至数千千米的云系系统尺度,故极为复杂,其相应的云量问题同样也是极为复杂的。Teixeira(2001)研究低云量与相对湿度的关系,从一个稳定的云量预报方程出发,得到了一个关于亚热带边界层云量诊断方程。Gu等(2003)从云的光学性质出发,改进了UCLA AGCM模式中云-辐射方案,对全球总云量的计算提高了5%的准确率。戴福山等(2004)提出了一个基于统计的低云参数化方案,用于CCM3模式后显著增强对大洋东部冷海域低云云量的模拟。Tiedtke(1993)通过对云形成与消散的影响因子研究,推导出云量预报方案。钱云(1994)在一个区域气候模式中引入了不同的云量计算方案,加以比较和改进后,成功地模拟出区域的夏季天气气候特征。王咏青等(2010)对大气模式中云量诊断的系统性误差进行研究,表明云量与其他变量的关系是由凸函数描述的,则云量会系统性地偏少;反之,如果云量与其他变量的关系是由凹函数来描述的,则云量会系统性地偏大。
全球/区域多尺度通用数值分析同化与预报系统(GRAPES)是中国自主发展的新一代数值预报系统,优化和完善其物理过程将提高模式对中国地区天气预报的能力,解决目前我国业务部门所运用的从国外引进的预报模式在中国地区预报效果普遍退化的问题(徐国强等,2008)。随着预报模式分辨率的提高、天气预报对预报对象和预报精度要求的提高,对物理过程的描述也越来越向精细化的方向发展,在引进国外的物理方案的过程中也要具体分析,不断改进和完善(闫之辉等,2010)。因此本文利用GRAPES区域模式,在模式中分别耦合国际上较为先进模式[欧洲中心的全球预报模式(ECMWF)和美国WRF模式]中的云量计算方案,对2008年5月29—31日的一次天气过程进行模拟,重点对比分析采用新云量方案后云的分布与云量的变化,以及对地面温度模拟的差异。目的是通过与GRAPES原方案的模拟结果进行对比分析研究,选择模拟效果较好的方案作为GRAPES新云量计算方案而引进,从而对GRAPES模式的云量计算方案进行改进和完善。
1 GRAPES模式与云量计算方案简介 1.1 GRAPES模式简介GRAPES(Global/Regional Assimilation and Prediction Enhanced System)模式是我国自主研发的一个多尺度通用模式,兼顾全球与有限区可选的预报区域设计,静力与非静力可选的平衡设计,采用半隐式-半拉格朗日时间差分方案,经纬度格点的网格设计,水平方向取Aracawa C格点,垂直方向采用Charney-Philips格式非均匀跳层变量配置,高度为地形追随坐标。模式的物理过程包括积云对流过程、微物理过程、辐射过程、边界层过程和陆面过程等(陈德辉等,2008;薛纪善等,2008)。
1.2 云量计算方案简介 1.2.1 GRAPES模式现用云量计算方案GRAPES模式现用云量计算方案(下文中简称GRAPES云方案)是云量诊断方案,体现相对湿度与云量之间的关系。首先计算出水面和冰面的饱和混合比。再根据温度区分云水和云冰,确定云水和云冰的比例系数faf(式1),并根据该比例系数计算云水、云冰的饱和比湿和rqs(式2):
| $ \left\{ \begin{array}{l} \mathit{faf}{\rm{ = 0}}{\rm{.0}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{t} \ge {\rm{273}}{\rm{.15}}\\ \mathit{faf}{\rm{ = }}\frac{{{\rm{273}}{\rm{.15 - }}\mathit{t}}}{{{\rm{40}}}}\;\;\;\;\;\;{\rm{273}}{\rm{.15 > }}\mathit{t}{\rm{ > 233}}{\rm{.15}}\\ \mathit{faf}{\rm{ = 1}}{\rm{.0}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{233}}{\rm{.15}} \ge \mathit{t} \end{array} \right. $ | (1) |
| $ \mathit{rqs}{\rm{ = }}\left({{\rm{1 - }}\mathit{faf}} \right) \times {\mathit{Q}_{{\rm{vsw}}}}{\rm{ + }}\mathit{faf} \times {\mathit{Q}_{{\rm{vsi}}}} $ | (2) |
式中,Qvsi为冰面饱和混合比,Qvsw为水面饱和混合比。
最后通过相对湿度计算云量,如式(3)~式(5):
| $ \mathit{RH}{\rm{ = min}}\left[ {{\rm{1}}{\rm{.0, }}\frac{{{\mathit{Q}_\mathit{v}}}}{{\mathit{rqs}}}} \right] $ | (3) |
| $ \begin{array}{l} \mathit{cc}{\rm{ = min}}\left\{ {{\rm{1}}{\rm{.0, }}\left[ {{\rm{1}}{\rm{.0 - exp}}\left({ - \frac{{{\rm{100(}}{\mathit{Q}_\mathit{c}}{\rm{ + }}{\mathit{Q}_\mathit{i}}{\rm{)}}}}{{{\mathit{Q}_{{\rm{vsw}}}}}}} \right)} \right]} \right. \cdot \\ \;\;\;\;\;\;\left. {{\rm{exp}}\left[ {{\rm{0}}{\rm{.25ln}}\left({\mathit{RH}} \right)} \right]} \right\} \end{array} $ | (4) |
| $ {\mathit{C}_\mathit{f}}{\rm{ = min}}\left[ {{\rm{1}}{\rm{.0, }}\mathit{cc}\left({{\rm{1 + 2}}{\mathit{Q}_{{\rm{vsi}}}}} \right)} \right] $ | (5) |
式中,Qc为云水混合比,Qi为云冰混合比,RH为相对湿度,Cf为云量。
1.2.2 WRF模式现用云量计算方案WRF模式现用的云量计算方案(下文中简称WRF云方案)也是一种云量诊断方案,在计算流程上与GRAPES云方案类似。不同的是在WRF云方案中,引入了对雪的判断,故在区分云水、云冰和雪是分为两种情况:(a)当云水、云冰和雪都存在时,如式(6),其中Qc为云水混合比,Qi为云冰混合比,Qs为云雪混合比;(b)只有云水存在时,如式(7)。
| $ \left\{ \begin{array}{l} \mathit{faf}\;\;{\rm{ = }}\;\;{\rm{0}}\\ \;\;\;\;\;\;\;\;{\mathit{Q}_i} + {\mathit{Q}_\mathit{c}} + {\mathit{Q}_s} < {10^{ - 12}}{\rm{kg}} \cdot {\rm{k}}{{\rm{g}}^{ - 1}}\\ \mathit{faf}\;\;{\rm{ = }}\;\;\frac{{{\mathit{Q}_i} + {\mathit{Q}_s}}}{{{\mathit{Q}_i} + {\mathit{Q}_s} + {\mathit{Q}_c}}}\\ \;\;\;\;\;\;\;{\mathit{Q}_i} + {\mathit{Q}_s} + {\mathit{Q}_c} \ge {10^{ - 12}}{\rm{kg}} \cdot {\rm{k}}{{\rm{g}}^{ - 1}} \end{array} \right. $ | (6) |
| $ \left\{ \begin{array}{l} \mathit{faf}\;\;{\rm{ = }}\;\;{\rm{0}}\\ \;\;\;\;\;\;\;\;{\mathit{Q}_\mathit{c}} < {10^{ - 12}}{\rm{kg}} \cdot {\rm{k}}{{\rm{g}}^{ - 1}}\\ \mathit{faf}\;\;{\rm{ = }}\;\;{\rm{0}}\\ \;\;\;\;\;\;\;{\mathit{Q}_\mathit{c}} \ge {10^{ - 12}}{\rm{kg}} \cdot {\rm{k}}{{\rm{g}}^{ - 1}}并且t > 273.15{\rm{K}}\\ \mathit{faf}\;\;{\rm{ = }}\;\;1\\ \;\;\;\;\;\;\;{\mathit{Q}_\mathit{c}} \ge {10^{ - 12}}{\rm{kg}} \cdot {\rm{k}}{{\rm{g}}^{ - 1}}并且t \le 273.15{\rm{K}} \end{array} \right. $ | (7) |
通过比例系数faf计算云水和云冰的饱和比湿rqs后[同式(2)],最后根据相对湿度计算云量,如式(8)~式(10):
| $ \mathit{RH}{\rm{ = max}}\left[ {{\rm{1}}{{\rm{0}}^{ - 10}}{\rm{, }}\frac{{{\mathit{Q}_\mathit{v}}}}{{\mathit{rqs}}}} \right] $ | (8) |
| $ \arg = \max \left[ { - 6.9, - \frac{{100{\mathit{Q}_\mathit{c}}}}{{\max \left({{\rm{1}}{{\rm{0}}^{ - 10}}{\rm{, }}\mathit{rqs} - {\mathit{Q}_\mathit{v}}} \right)}}} \right] $ | (9) |
| $ c_f = \frac{{R{H^b}}}{a}\left[ {1 - \exp \left({\arg } \right)} \right] $ | (10) |
式中,a=1.0, b=0.25,RH为相对湿度,Cf为云量。
1.2.3 ECMWF云量计算方案EC模式的云量计算包括预报和诊断两种方案,在本文中为了保证4种云方案对比的一致性,选取EC诊断云方案进行说明和对比。
该方案(下文中简称EC云方案)包含对4种类型云的计算(Siingo,1987):对流云(积云和积雨云)、高云(卷云)、中云(高层云和高积云)、低云(层云和层积云)。单层云量的计算来源于对流云量和用相对湿度阈值法计算的大尺度云量。
对流云量根据对流性降水的降水率进行计算,
| $ {C_c} = a + b\ln \mathit{P} $ | (11) |
其中,Cc为对流云量,P为对流性降水的降水率,单位为mm·d-1, a和b为经验值。
| $ {C_f} = rc \times {C_c} + {\left({\frac{{rh - crh}}{{1 - crh}}} \right)^2} \times w \times rl $ | (12) |
式中,rc为对流云塔的权重系数,rh为存在对流的相对湿度,crh为与低云和高云临界湿度有关的量,w为垂直速度,rl为与低云翻转有关的量,Cf为云量。
1.2.4 简单云量计算方案简单云量计算方案(下文中称简单云方案)是WRF和GRAPES模式原来采用的云量计算方案,该方案原理相对简单,通过云水和云冰的混合比直接判断格点上云量的有无:
| $ \left\{ \begin{array}{l} {\mathit{Q}_\mathit{c}} + {\mathit{Q}_i} > {10^{ - 6}}{\rm{kg}} \cdot {\rm{k}}{{\rm{g}}^{ - 1}}\;\;\;\;\;{C_f} = 1\;\;\;有云\\ {\mathit{Q}_\mathit{c}} + {\mathit{Q}_i} \le {10^{ - 6}}{\rm{kg}} \cdot {\rm{k}}{{\rm{g}}^{ - 1}}\;\;\;\;\;{C_f} = 0\;\;\;无云 \end{array} \right. $ | (13) |
该方案引入水汽含量、云水含量、雨水含量、云冰含量、雪含量和霰含量6个预报量,考虑了云-降水自动转化、冰晶核化、云水的冻结、冰晶的繁生、降水碰并云水、雨水的凝结和蒸发,冰雪晶的凝华和升华及云水的凝结和蒸发等微物理过程。该方案在WSM3和WSM5云微物理方案的基础上,增加了霰及其相关过程的计算。并且对混合相粒子的下落速度由同一速度的改进为由混合比来计算。在粗网格过程中,WSM6方案与WSM3和WSM5方案的差异较小,但是在考虑了计算效率和理论背景的情况下,WSM6方案更适合有云的网格尺度计算。
2 资料与数值试验方案设计 2.1 资料美国NCEP每日4次的再分析资料, 水平分辨率为1°×1°,用于作为模式的初始场和侧边界条件场,观测资料包括:(1) 风云二号气象卫星拍摄的可见光云图,云图通过国家卫星气象中心的网站获得;(2) 每3小时一次的地面观测资料(MICAPS地面填图资料),要素包括总云量和地面温度,资料来源于中国气象科学研究院的大气科学信息部。
2.2 数值试验方案设计本文对2008年5月29日00时至5月31日00时(UTC,以下时间均为世界时)的天气过程进行了模拟。初始积分时间是2008年5月29日00时(UTC),时间步长取为120 s,共积分48 h;水平格距取0.5°,垂直方向为不等距的26层,模式层顶高度为35000 m。模式区域范围为15°~60°N、70°~150°E。物理过程参数化方案采用如下选择:WMS6微物理过程方案,RRTM长波和Goddard短波辐射方案,M-O近似的近地面层方案,热辐散(thermal diffusion)陆面过程方案,MRF边界层方案以及Betts-Miller-Janjic对流参数化方案。
设计4种试验方案如下:
数值试验1:利用GRAPES模式现用的云量计算方案进行数值试验;
数值试验2:引进ECMWF模式的云量计算方案,替换GRAPES模式中现用的云量计算方案;
数值试验3:引进WRF模式的云量计算方案,替换GRAPES模式中现用的云量计算方案;
数值试验4:使用简单云量计算方案,替换GRAPES模式中现用的云量计算方案。
将这4种云量计算方案模拟得到的云分布与风云二号卫星云图进行对比,模拟的总云量分区域与观测资料对比,检验各种云量参数化方案对云量和云分布模拟的准确性。再将模拟的地面温度与观测的地面温度值进行对比,检验GRAPES模式采用不同云量参数化方案时对地面温度模拟的准确性。
3 数值试验结果分析 3.1 云分布模拟对比将模拟出的三维云量进行垂直叠加,叠加方法采用最大值平均,即先求每一个云块(即两层晴空间的有云区域)的垂直平均云量,再比较垂直方向上不同云块平均云量的最大值,作为总云量。将总云量的分布视为云区,并与风云二号气象卫星云图进行对比。对比时次分别选取为2008年5月29日06时和5月30日06时。
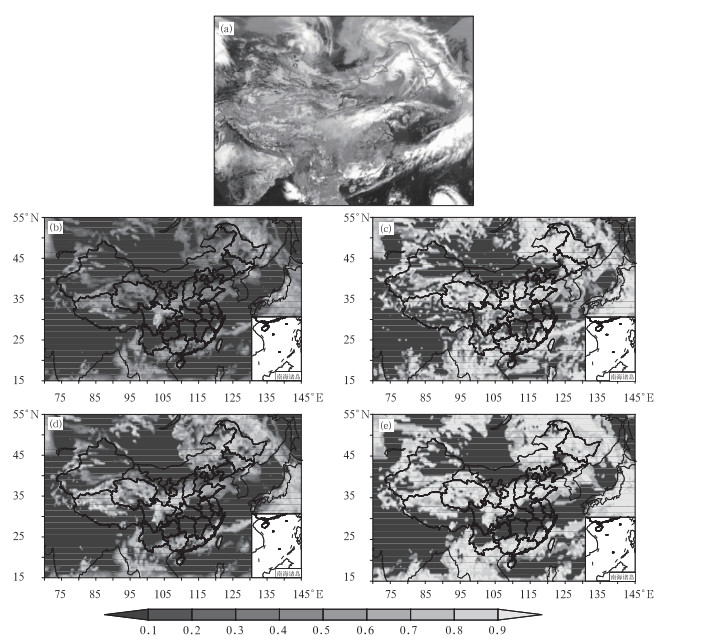
由5月29日06时的卫星云图(图 1a)可以看出我国云区主要分布在东北、黄河流域及两广一带。图 1a中云的颜色越白亮表示该区域云层越深厚,灰色则表示云层较浅薄,因此东北北部的逗点状云系、黄淮地区的云带和广东的云团为主要的深厚云层。图 1b~1e表示通过4种不同云量计算方案模拟出的云分布,图中数值越大表示该区域云量越多,云层越厚。由图看出4种云量计算方案都能较为准确地模拟出云区的主要位置,但不同方案模拟的云区的范围有一定差异。其中GRAPES和WRF云方案的模式模拟出的总云量较其他两种方案偏少,云区也相对偏小,只能大致模拟出深厚云层的中心位置,并没有模拟出云的全部范围,同时对于青藏高原上空的较薄云层也没有完整地模拟出来。而EC和简单云方案的模式模拟的云区范围更符合实况分布,东北地区的逗点状云系模拟较为完整,也大致模拟出了青藏高原到西南地区的浅薄云层。
|
图 1 2008年5月29日06时云分布 (a)风云二号卫星可见光云图, (b)GRAPES云方案, (c)EC云方案, (d)WRF云方案, (e)简单云方案 Fig. 1 The cloud coverages at 06:00 UTC 29 May 2008 from (a) VIS satelite image of FY-2, (b) GCFS, (c) ECFS, (d) WCFS, and (e) SCFS |
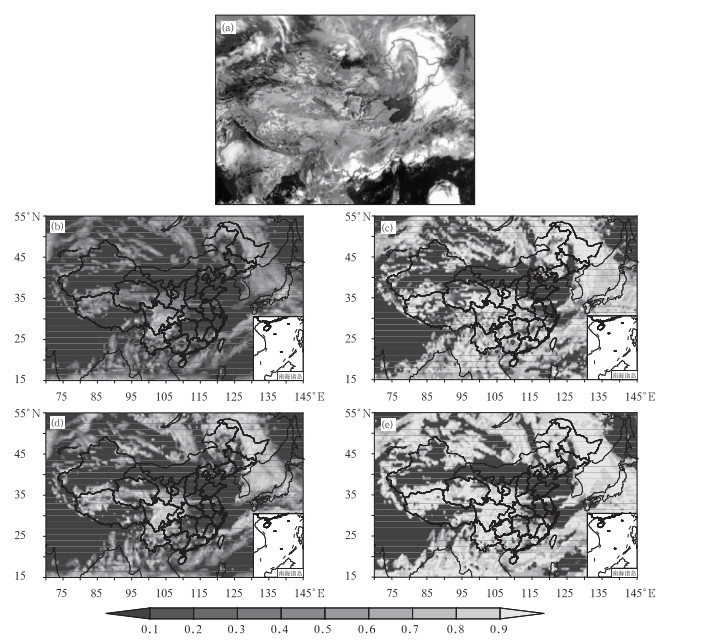
由5月30日06时的卫星云图(图 2a)可以看出,和5月29日06时相比,逗点云系范围扩大并且向东北方向移动,黄淮地区的云带南移与两广地区的云区连成一片,因此我国北方大部分地区为晴空区,南方有大范围云区。图 2b~2e表现出,4种云量计算方案的模式都能较为准确地模拟出云区的主要位置,但GRAPES和WRF云方案模拟的区域相对偏小。与之相对比,采用EC云方案和简单云方案模拟的云区更符合实际云分布状况。对长江中下游平原和青藏高原上空的的阴云区,EC云方案比其他三种云方案模拟更为准确。
|
图 2 2008年5月30日06时云分布 (a)风云二号卫星可见光云图,(b)GRAPES云方案,(c)EC云方案,(d)WRF云方案,(e)简单云方案 Fig. 2 The cloud coverages at 06:00 UTC 30 May 2008 from (a) VIS satelite image of FY-2, (b) GCFS, (c) ECFS, (d) WCFS, and (e) SCFS |
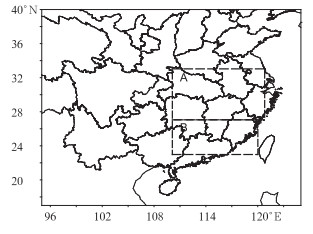
单个时次的云分布状况只能反映出模拟的云区与实况是否吻合,无法准确反映某区域内云量的平均值与实况的关系。为更准确地分析这几种云量计算方案的优劣,将模拟的云量与地面观测云量(每3小时一次的MICAPS地面填图资料)进行了对比分析。由于观测资料站点分布不均匀,为了保证观测资料的准确性,故选取观测站点较为密集的长江中下游地区(图 3中A区,27°~33°N、110°~121°E)和华南地区(图 3中B区,23°~27°N、110°~120°E)。将区域内模拟的单层云量垂直叠加为总云量后,用双线性插值法插值到区域内的站点上,其中,A区域有96个站点,B区域有20个站点。再分别计算这两个区域内站点云量的平均值,做模拟云量和观测云量随时间变化的对比分析。
|
图 3 选择的对比区域 (A:长江中下游地区,B:华南地区) Fig. 3 Contrast areas A and B (A: The middle and lower reaches of Yangtze River, B: South China) |
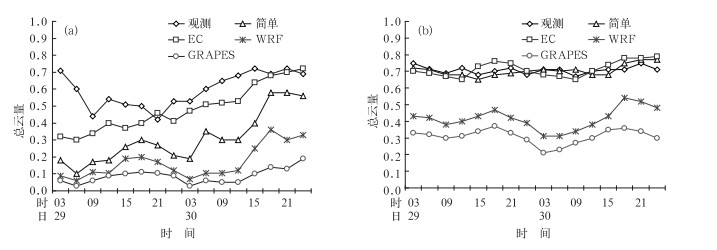
图 4a表现的是模拟总云量与观测总云量在长江中下游地区随时间变化的对比,从图中整体来看,模拟的总云量随时间变化的趋势与观测值较为一致,都呈增加的趋势。但4种方案模拟的云量分别不同,EC云方案模拟的云量最多,也较为接近观测值,简单云方案次之,WRF和GRAPES云方案模拟的总云量都偏少,其中GRAPES云方案模拟的云量最少。从华南地区的总云量对比(图 4b)可以看出,观测的总云量随时间变化较为平缓。模拟的总云量中,EC与简单云方案的模拟值较为接近观测值,WRF和GRAPES云方案模拟的总云量较观测值偏少,并且随时间变化的波动较大。
|
图 4 2008年5月29日03时至31日00时总云量随时间的变化 (a)长江中下游地区,(b)华南地区 Fig. 4 The evolution of total cloud fraction (03:00 UTC 29-00:00 UTC 31, May 2008) in (a) the middle and lower reaches of Yangtze River, and (b) South China |
从4种方案的特点来说,WRF和GRAPES云方案是云微物理量和相对湿度结合的方法, 考虑的是一种静态的过程,通过云微物理量的各相态含量比例,求得相对湿度,再通过经验公式判断云量多少。云微物理量是用显式云方案计算的,考虑的宏微观因子和过程全面,但在粗网格模式中不能描述次网格尺度的对流云,从而影响到云量计算准确性的问题,使得在积云量较多的情况下,计算的总云量偏少。EC云方案完全不依赖显式云方案,直接从对流降水中推导对流云量,加上用相对湿度阈值法计算大尺度云量,对于粗网格模式是可行的。在本个例中,对流降水占总降水的80%左右,故EC云方案模拟的云量较好。同时,云的形成的发展过程中存在着动力过程,特别是在低云的形成与发展过程中,强烈的上升运动和与环境空气的相互作用等宏观物理过程发挥着重要的作用。这种依赖宏观物理量和微物理因子相互结合计算云量的方法在EC云方案中体现,可能因此计算结果也就更接近实际情况。而简单云方案是只依赖云微物理量决定云量的方法,虽然方法简单,但判定是否有云的临界值也可以经过多次调节达到最优值,故对总云量的判断效果较好,但是计算方法考虑的影响因素太少,对云量的计算依然存在一定偏差。因此4种方案相比较,EC云方案对云量计算的原理更加合理,模拟效果更加准确。
3.3 温度场模拟对比云对太阳辐射与地球辐射都具有很大的光学厚度,在地气系统的辐射收支中起支配作用。一方面,云是太阳的良好反射体,它将部分入射太阳辐射反射回外太空,对其下的大气和地面起冷却作用;另一方面,云又是地球和大气辐射的强吸收体,即云能够吸收地表的长波辐射,并向下发射长波辐射,对地球表面起加热作用(石广玉,2007)。从云在地气系统的辐射能量收支中产生的对地面温度影响的作用来说,它不仅依赖于云量及其分布,而且依赖于云所在的高度,含水量以及云的微物理特性等。由于在模式中采用了相同的云微物理方案,因此对地面温度模拟的差异,就体现在模式的辐射计算中采用了不同云量计算方案,模拟的云量与分布的不同所致。在计算方案中根据云量的多少将大气区分为有云区和晴空区,在有云覆盖的情况下,大气中就形成了额外的边界,云底吸收来自地面和低层大气的长波辐射,云顶将部分太阳短波辐射反射回外太空。反之,在晴空区就会接收到更多的太阳短波辐射。再通过计算净辐射通量密度,得到加热率的大小,进而得到地面温度。
为了体现云量对地面温度的影响,选取观测的地面温度场资料与模式模拟的地面温度场进行对比,对比时次选择为30日00时(积分24 h)和31日00时(积分48 h)。
图 5为采用4种不同云方案的模式模拟的地表温度与观测温度在5月30日00时的差值分布。总体来说,4种方案模拟出的地面温度大致类似,是因为在模式中采用了相同的陆面参数化过程所致。从图上看出模拟的地面温度在青藏高原地区都偏低,偏低幅度在5℃以上,在新疆的中东部地区模拟的温度偏高于观测值5℃以上,而在整个中东部地区,包括华北、华中、华南和西北东部地区,模拟的温度与观测值较为接近,平均差额在±5℃以内。从采用了不同云量方案的模拟结果来看,在四川西部与西藏交界的横断山脉地区(图上的虚线框区域)模拟的温度有所差异,在该区域(图 5b)的深色范围明显小于其他3图,说明在该区域,采用EC云方案模拟出的地面温度与实测温度差距较小,更接近于实测值。
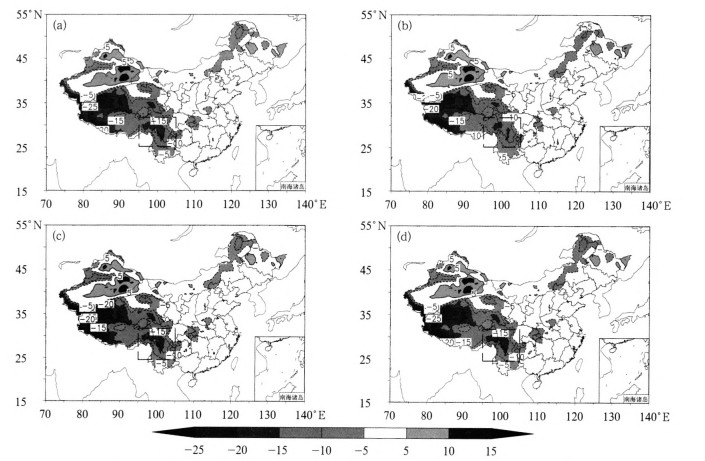
|
图 5 2008年5月30日00时模拟的地面温度与观测的地面温度的差值分布(单位:℃)
(a)GRAPES-观测,(b)EC-观测,(c)WRF-观测,(d)简单-观测 (虚线框为采用不同云量方案的模拟结果) Fig. 5 The difference distribution between observed and simulated surface temperatures at 00:00 UTC 30 May 2008 (unit:℃) (a) GCFS-Obs, (b) ECFS-Obs, (c) WCFS-Obs, (d) SCFS-Obs |
图 6为采用4种不同云方案的模式模拟的地表温度与观测温度在5月31日00时的差值分布,总体来说,4种方案模拟出的地面温度也大致相同。与实测相对比,在青藏高原地区都偏低,幅度达10℃以上,在新疆的中东部地区到内蒙古的西部地区模拟的温度偏高于观测值5℃以上,而在包括华北、华中和华南的中部地区,模拟的温度与观测值较为接近,平均差额在±5℃以内。就采用了不同云量方案的模拟结果来看,在四川东部与陕西南部(图上的虚线框区域)模拟的温度有所差异,在该区域(图 6b)的灰色范围明显小于其他3图,说明在该区域,采用EC云方案模拟出的地面温度与实测温度差距较小,更接近于实测值。
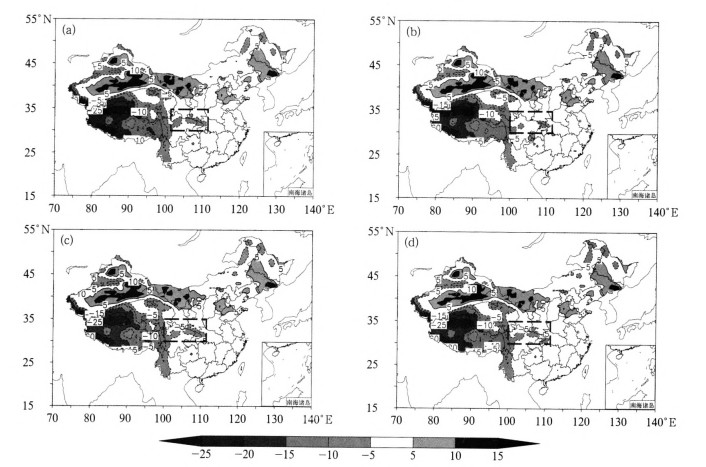
|
图 6 2008年5月31日00时模拟的地面温度与观测的地面温度的差值分布(单位:℃) (a)GRAPES-观测,(b)EC-观测,(c)WRF-观测,(d)简单-观测 Fig. 6 As in Fig. 5, but for 00:00 UTC 31 May 2008 (a) GCFS-Obs, (b) ECFS-Obs, (c) WCFS-Obs, (d) SCFS-Obs |
为了更清楚地说明采用不同云方案的模式对地面温度模拟的准确性。对上文所述的30日00时和31日00时的温度差做区域平均,分别进行对比。
从表 1中可以看出在该个例中,采用了EC云方案的模式模拟的地面温度在全国范围内比采用其他三种方案模拟得更接近实测约0.2~0.3℃,在选定的区域内,采用EC云方案的模式模拟的地面温度比采用其他三种方案模拟得更接近实测1℃左右,因此说明了采用EC云方案的模式能相对提高GRAPES模式对地面温度预报的准确性。
|
|
表 1 全国和区域范围内观测与模拟的地面温度差值(单位:℃) (区域表示上文中的虚线框范围,全国表示全国范围) Table 1 The difference between observed and simulated surface temperatures in national and regional scale (unit: ℃) (Regional shows the dotted box in the above, national shows nationwide) |
从以上分析可以得到,模式分别采用4种云量计算方案模拟的地面温度与实际观测对比分析,在中国东部地区模拟的地面温度与观测基本接近,但在中国西部地区则误差较大;引起误差较大的原因一方面可能是模式本身对青藏高原区域和新疆沙漠地带模拟得较差,模式性能有待改进;另一方面原因,也可能是中国西部观测站点较稀少,使观测与模拟的误差较大。总起来看,EC云方案模拟出的地面温度与实测温度差距相对较小,与其他方案相比,更具有优越性。
4 小结在GRAPES模式中分别引进了EC云量计算方案、WRF云量计算方案,并与GRAPES现用的云量计算方案和简单云方案对一个个例进行了对比数值试验,试验结果与观测数据进行了对比分析,得到了一些有益的结论:
(1) 通过模拟的云分布状况与风云二号卫星可见光云图的对比,表明4种云量计算参数化方案都能大致模拟出云带的分布,但EC与简单云方案模拟的云分布更为准确,WRF和GRAPES云方案模拟的云分布区域偏小。
(2) 通过模拟的总云量与地面观测云量随时间变化的对比,表明GRAPES和WRF云方案模拟的总云量偏少,EC和简单云方案模拟的总云量较为接近观测值。
(3) GRAPES模式采用4种不同云量计算方案模拟出的地面温度场与观测值相对比,在中国东部地区模拟的地面温度与观测基本接近,但在中国西部地区则误差较大;从全国和局部区域的地面温度平均值对比中发现,采用EC云方案时模式模拟的地面温度更接近观测值。
(4) 通过在GRAPES模式中采用不同云量计算方案进行数值试验,综合分析模拟结果与观测值的对比效果,认为EC云量计算方案模拟的效果最佳,可以作为一种新的云量计算方案引进GRAPES模式中。
需要指出的是,以上结论只是在对一次天气过程的模拟分析的结果;同时也看到,无论采用哪种云量计算方案,GRAPES模式对中国西部高原和沙漠地区的地面温度模拟都较差,需要对该地区的陆面过程、边界层过程、辐射过程以及其他物理过程方案进行更深入的研究,不断地对其进行改进和完善;对这一区域的观测也应该不断加密,以得到更准确的观测数据。
陈德辉, 薛纪善, 杨学胜, 等, 2008. GRAPES新一代全球/区域多尺度统一数值预报模式总体设计研究[J]. 科学通报, 53(20): 2396-2407. DOI:10.3321/j.issn:0023-074X.2008.20.002 |
戴福山, 宇如聪, 张学洪, 等, 2004. 一个统计低云方案及其在大气环流模式中应用初探[J]. 气象学报, 62(4): 385-394. DOI:10.11676/qxxb2004.039 |
钱云, 1994. 区域气候模式中云量参数化方案的研究[J]. 热带气象学报, 10(4): 342-348. |
石广玉, 2007. 大气辐射学[M]. 北京: 科学出版社, 134-135.
|
王咏青, 张楠, 刘敏, 等, 2010. 大气模式中云量诊断的系统性误差研究[J]. 气候与环境研究, 15(1): 83-88. |
薛纪善, 陈德辉, 2008. 数值预报系统GRAPES的科学设计与应用[M]. 北京: 科学出版社, 331-342.
|
徐国强, 陈德辉, 薛纪善, 等, 2008. GRAPES物理过程的优化试验及程序结构设计[J]. 科学通报, 53(20): 2428-2434. DOI:10.3321/j.issn:0023-074X.2008.20.006 |
徐兴奎, 2012. 中国区域总云量和低云量分布变化[J]. 气象, 38(1): 90-95. DOI:10.7519/j.issn.1000-0526.2012.01.010 |
闫之辉, 王雨, 朱国富, 2010. 国家气象中心业务数值预报发展的回顾与展望[J]. 气象, 36(7): 26-32. DOI:10.7519/j.issn.1000-0526.2010.07.007 |
章建成, 刘奇俊, 2006. GRAPES模式不同云物理方案对短期气候模拟的影响[J]. 气象, 32(7): 3-12. DOI:10.7519/j.issn.1000-0526.2006.07.001 |
Gu Y, Farrara J, 2003. Parameterization of cloud-radiation processes in the UCLA general circulation model[J]. J Climate, 16(2): 3357-3370. |
Teixeira J, 2001. Cloud fraction and relative humidity in a prognostic cloud fraction scheme[J]. Mon Wea Rev, 129(7): 1750-1753. DOI:10.1175/1520-0493(2001)129<1750:CFARHI>2.0.CO;2 |
Tiedtke M, 1993. Representation of clouds in large-scale models[J]. Mon Wea Rev, 121(11): 3040-3058. DOI:10.1175/1520-0493(1993)121<3040:ROCILS>2.0.CO;2 |
Tompkins A M, 2002. A prognostic parameterization for the subgrid-scale variability of water vapor and clouds in large-scale models and its use to diagnose cloud cover[J]. J Atmos Sci, 59(12): 1917-1942. DOI:10.1175/1520-0469(2002)059<1917:APPFTS>2.0.CO;2 |
Slingo J M, 1987. The development and verification of a cloud prediction scheme for the ECMWF model[J]. Quart J R Met Soc, 113(447): 899-927. |
Sommeria G, 1977. Subgrid-scale condensation in models of nonprecipiting clouds[J]. J Atmos Sci, 34(2): 344-355. DOI:10.1175/1520-0469(1977)034<0344:SSCIMO>2.0.CO;2 |
 2013, Vol. 39
2013, Vol. 39 
