引言

集合预报作为最新发展的新一代动力随机预报技术，被世界气象组织(WMO)列为未来数值预报的四大发展方向之一。1992年12月美国国家环境中心(NCEP)(Toth et al，1997)和欧洲中期天气预报中心(ECMWF)(Molteni et al，1996)的中期集合预报投入业务运行，随后中期集合预报系统开始在国外的数值预报业务体系中发挥越来越大的作用。随着计算机的快速发展和中期集合预报的成功，Brooks等(1995)首先试验了短期集合预报应用在数值天气预报中的可行性。至此以后，越来越多的研究工作者致力于短期集合预报，主要集中在强降水过程(Du et al，1997; Hamill et al，1997)、温带气旋的爆发(Stensrud et al，1999)及其他高影响天气等。例如Du等(1997)利用中尺度模式进行短期集合预报研究了初始条件不确定性对于定量降水的影响。Hamill等(1997)研究指出短期集合预报有利于提高降水概率预报(PQPFs)。Stensrud等(1999)利用Eta模式进行气旋位置预报，发现水平分辨率为80 km的集合平均预报与29 km的单一确定性预报具有的预报性能相当。

我国是世界上较早研究和建立集合预报系统的国家之一，在短期集合预报技术和应用方面取得了一定的进展。王晨稀等(2003)利用MM5模式通过不同的物理参数方案对1999年华东地区梅雨期间的3个降水个例进行48 h集合预报，指出不同集合成员的预报结果各不相同，积云参数化方案对降水的影响比边界层参数化方案对降水的影响大。陈静等(2003a; 2003b)利用不同物理过程参数化方案组合的模式扰动法开展中国暴雨短期集合预报的可行性，结果表明在短期数值预报中，非绝热物理过程对高度场预报影响较小，但边界层方案和对流参数化方案对产生暴雨的3个基本条件影响很明显；对中国热力场较均匀的暴雨过程，可以通过扰动模式的边界层和对流参数化方案，构造集合预报模式。陈超辉等(2009)利用多模式进行2003年江淮汛期短期集合预报方法研究，指出不同的模式对于降水响应不同。周霞琼等(2003)用正压模式进行了热带气旋路径集合预报试验，指出滞后平均法对热带气旋路径预报具有较好的改进作用。

虽然短期集合预报的研究应用已有了初步成效，但往往空间尺度小、生命周期短的突发性强灾害天气过程对人民的生命财产带来的威胁更大，例如雷暴、局地大暴雨等。WMO 2005年定义的临近预报为0~6 h的天气预报，而短期集合预报主要提供区域内0~48 h间的预报，例如降水预报往往关注6 h以上的累积降水，同时其水平分辨率主要在10 km以上(王晨稀等，2003；陈静等，2003a; 2003b；Yuan et al，2007)，有时不能捕捉到一些中小尺度的系统而导致漏报，无法满足人们对短时临近天气预报的需求。当前国内业务上应用的短时临近预报一般基于雷达资料、卫星资料的外推，部分地区建立了区域短时临近天气预报系统。虽然这些短时临近预报技术对于强对流天气提供了一定的指示作用，但大部分预报产品的时效太短，仅为1 h(Chen et al，2009)。NCEP(Zhou et al, 2010)利用现有的快速更新循环(Rapid Update Cycle)和北美中尺度(North American Mesoscale)两个模式的资料输出，采用时间滞后的方法研发甚短期集合预报系统(Very Short Range Ensemble Forecast System, VSREF)，已开发出11个与航空天气相关的概率产品，开展的能见度检验表明其预报具有正技巧。但目前国内短时临近集合预报的研究依旧是块空白，需要尽快开展相关方面的研究及应用，使其在防灾减灾中发挥应有的作用。

本文尝试在华东区域中尺度快速更新同化数值预报模式系统SMB-WARR(Shanghai Meteorological Bureau WRF ADAS Rapid Refresh)基础上，通过时间滞后的集合方法构造产生了7个集合成员，并对2011年6月17日至9月30日期间的上海地区降水进行短时临近集合预报试验，以面雨量的形式进行检验，以尝试提高对大城市精细化短时临近预报的能力。

1 模式与资料

试验模式为华东区域中尺度快速更新同化数值预报模式系统SMB-WARR(陈葆德等，2011)，该模式的预报范围覆盖华东区域，计算区域中心位置为(30.0°N、119°E)，水平分辨率为3 km，格点数为525×625，垂直层次为51层。模式主要针对短时临近天气，为每小时起报一次，预报时效为12 h，24 h循环，其中在每日的18时(UTC，下同)进行冷启动。系统初猜场为GFS每日12时起报的6 h预报场，其余时刻的初猜场为SMB-WARR的1 h预报场，通过ADAS系统同化观测数据后得到模式初始场，边界场由GFS每日12时预报场给出。模式采用非静力框架，微物理过程为WSM 6-class，边界层采用MYJ方案，陆面及地表过程分别为Noah及Monin-Obuknov，辐射方案分别为RRTM及Dudhia，没有考虑积云参数化过程。

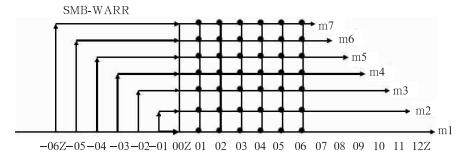
2 集合成员构成

基于SMB-WARR模式，采用时间滞后的集合方法，即用相距1 h的不同时刻初始场分别作预报，然后用预报相同时刻的结果构造集合成员，如图 1所示。以00 Z的为例，集合成员包含00 Z、-01 Z、-02 Z、-03 Z、-04 Z、-05 Z、-06 Z, 共7个成员，分别记为m1、m2、m3、m4、m5、m6、m7，预报时效为6 h，即图 1所示的01、02、03、04、05和06 Z。以SMB-WARR提供的集合所需的成员，经过后处理，实现每小时起报一次，预报时效为6 h，以24 h作为一次完整的循环周期的短时临近集合预报系统。

3 集合预报检验

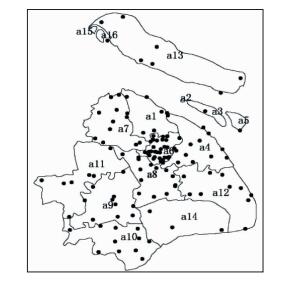
对2011年6月17日至9月30日期间的上海地区降水进行短时临近集合预报试验，以面雨量的形式进行检验，检验方法主要有TS评分、偏差B、漏空报、Talagrand分布、Brier Skill Score等。目前，国内外就面雨量的分级还没有统一的标准，尤其是1 h面雨量，本文参考董官臣等(2000)其对区域性降水量级面雨量的界定方法，同时基于1 h格点上的降水分级，将面雨量分成小雨(0.1~1.0 mm)、中雨(1.0~4.2 mm)、大雨(4.2~9 mm)、暴雨(9~24 mm)、大暴雨(24~30 mm)等5个量级，分别检验每个量级1 h的预报情况，由于预报资料为逐小时输出，同时水平分辨率较高，检验依据上海地区的自动站资料作为实况。图 2为上海地区的自动站分布情况，将整个上海划分为16个区域(分别记为a1~a16，包括中心城区、8个郊区、1个郊县及5个小岛)，采用算术平均法进行面雨量计算。由于观测实况或预报的数据部分缺失，检验的有效样本为，小雨(2453例)、中雨(998例)、大雨(305例)、暴雨(137例)；大暴雨(6例)暂不考虑。

3.1 集合平均预报

假设实况比预报雨量低一个等级记为空报，实况比预报雨量高一个等级为漏报，否则击中报对，则TS评分、空报率FAR、漏报率NAR、偏差B的计算公式如下(公颖，2007；陈静等，2003a; 2003b；孟英杰等，2008)：

$ TS = NA/\left( {NA + NB + NC} \right) $

(1)

式中：NA、NB、NC分别代表报对、空报、漏报的区域个数。当预报与实况的降水区域个数完全一致时，则TS=1，TS越趋近于0，表明预报技巧越差。

$ FAR = NB/\left( {NA + NB} \right) $

(2)

$ NAR = NC/\left( {NA + NC} \right) $

(3)

$ B = \left( {NA + NB} \right)/\left( {NA + NC} \right) $

(4)

FAR和NAR值越小表示预报技巧越高，二者均为0时说明模式预报完美。而偏差B中小于1代表漏报多，大于1代表空报多。

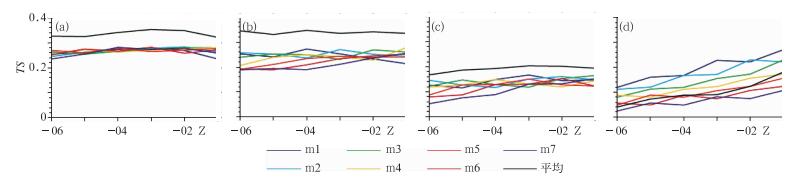
图 3为各降水量级所有集合成员与集合平均预报(这里指等权平均)的TS评分，得到结果如下：(1) 平均而言集合成员的TS评分随降水量级增大而减小，小雨最高，中雨次之，其次是大雨和暴雨，但随着降水量级的增大，集合成员之间的预报技巧差异变大，尤其是暴雨量级，且部分集合成员的TS评分比大雨时的集合成员预报要高；(2) 小-大雨量级集合平均TS评分比所有集合成员要高，表明集合预报技术可在原有单一模式基础上提高降水预报性能，但由于平滑作用，暴雨量级集合平均TS评分不如部分集合成员好；小-中雨量级集合平均的表现相当，大-暴雨量级时集合平均的预报技巧明显降低；(3) 小-大雨量级的TS评分随起报时刻的变化浮动较小，预示着可以提前6 h预报，同时说明并非都是最接近预报时刻，技巧最高；(4) 暴雨量级的TS评分随预报时刻的临近而增大，可关注最接近预报时刻。此外，本文使用的暴雨样本(137例)较少，可能会对暴雨量级的检验结果产生一定的影响。

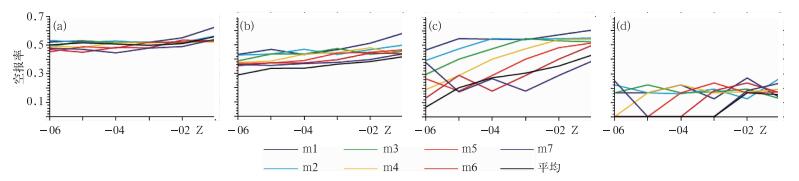
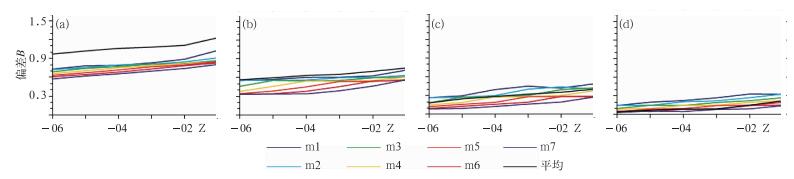
图 4为集合成员和集合平均的空报率，可见空报率随降水量级的增大而减小，大雨及以上，尤其是暴雨量级空报率值比其他量级的要偏小，起报时刻为-06 Z~-03 Z, 集合平均和部分集合成员出现空报率为零，说明对于暴雨量级，模式预报的降水偏弱。而集合平均出现空报率的可能相对于所有集合成员处于中间略偏小的位置，例如图 4b集合平均的空报率低于所有集合成员；而漏报率的集合成员之间的统计结果基本与空报率相反(图略)，但集合平均在小-大雨量级时漏报率一直低于所有集合成员，只在暴雨量级时，集合平均稍高于部分集合成员。为了更好地再现集合预报对于降水的相对漏空报情况，进行偏差B评分。从图 5a可见，只在小雨量级时集合平均出现偏差B大于1，说明集合平均在小雨量级时出现空报的可能最大，但总体而言无论是集合成员或是不同的降水量级，出现小于1的更多，即模式更偏向于漏报或者说强度报得偏弱，且降水量级越大，漏报情况更明显，集合平均的变化幅度更大。

综合分析分级降水的TS评分、漏空报情况可见小-大雨量级时，集合平均要优于集合成员预报，而暴雨量级，集合平均不及部分集合成员，但是暴雨样本有限，还需要更多的资料来进一步验证。

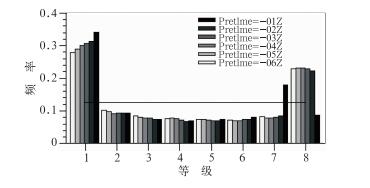
3.2 集合预报可靠性分析

一个好的预报系统必须满足的首要条件就是可靠性(马清等，2008)，采用Talagrand分布进行分析，它是用来检验预报值和检验值是否都是来自相同的概率分布(Hou et al，2001)。Talagrand等(1997)认为一个“好”的集合预报系统的标准是每个成员似乎以相同的概率发生。在本研究中理想的平均概率应当为1/8, 由各个成员概率分布绘制的Talagrand分布(如图 6)，可以发现不同起报时刻的Talagrand分布基本偏U型，等级为1时的概率相对较高，主要由于小量级降水空报现象较多造成的，同时等级为8的概率也高于理想概率，这与降水量级较大时模式预报偏弱有关。从Talagrand分布说明时间滞后的集合预报系统有一定的降水预报效果，但是其离散度还不够理想，这与Lu等(2007)使用RUC系统进行时间滞后短时临近集合预报时对于温、压、湿、风(不包括降水)的离散度检验结果较为一致。导致较小的离散度原因有(Hamill, 2001)：第一时间滞后的集合预报系统是有单一的模式集合构成，无法很好地展现不同模式之间的差别，而不同模式之间可以引起很大的集合离散度；第二集合成员直接来自预报，没有进行繁殖循环；第三集合成员的初始时间太接近，尤其是本文中的成员需为下一个成员提供初猜场, 使得原本就小的差距在相同模式动力过程中变得更小；第四少量的集合成员降低了捕捉到所有预报不确定性的能力。度量集合预报优劣的另一个标准是Q值，本文的概率均方差Q=0.09，一般Q值越小越好，表明集合预报更高的可信度。

3.3 概率预报

集合预报是单一确定性预报向多值的概率预报转变的关键技术基础(陈静等，2002；杜钧等，2010)，概率预报是表达集合预报最全面的方法之一。由于每一种检验方法对系统表现都有其特殊的含义，故应综合各种不同的检验方法来评估集合预报、概率预报的表现(Hou et al，2001)。Brier技巧评分(Brier Skill Score，BSS)(Brier，1950)针对不同量级以上降水概率预报应用价值进行检验。同时采用ROC(Relative Operating Characteristics)(Mason，1982)曲线检验不同量级以上降水概率对于天气事件的分辨能力。此外，针对不同量级以上降水，检验不同降水概率预报等级对应的TS评分高低，了解不同概率等级预报的可用性。

3.3.1 Brier Skill Score

Brier(1950)定义了一种均方概率误差, 其综合考虑了可靠性、分辨能力和不确定性，该方法已在定量降水概率预报评估中得到了广泛应用(Ferro，2007)，计算公式如下：

$ BS = \frac{1}{N}\sum\limits_{i = 1}^N {{{({f_i} - {o_i})}^2}} $

(5)

式中，N为二分类事件的预报数，f_i表示某一天气事件发生的预报概率，o_i表示实况(当事件发生时取1，事件不发生时取0)，其值越小越好，BS为0表示概率预报最佳，BS为1表示预报失效。基于BS，常用的Brier技巧评分，计算公式如下：

$ BSS = (B{S_{{\rm{ref}}}} - B{S_{\rm{f}}})/(B{S_{{\rm{ref}}}} - B{S_{{\rm{per}}}}) $

(6)

式中，BS_ref、BS_f、BS_per分别表示参考预报、集合概率预报、完美概率预报的BS评分。BS_ref通常使用气候平均概率预报的BS评分，本文计算中采用集合平均的BS评分。完美概率预报的BS评分BS_per=0，因此式(6) 表示为：

$ BSS = (B{S_{{\rm{mean}}}} - B{S_{\rm{f}}})/B{S_{{\rm{mean}}}} $

(7)

式中BSS表示了概率预报对集合平均预报的改进程度，BSS>0，表示概率预报有意义，当BSS＜0, 表示概率预报不如集合平均预报，当BSS=0时，表示概率预报的技巧与集合平均预报相当。

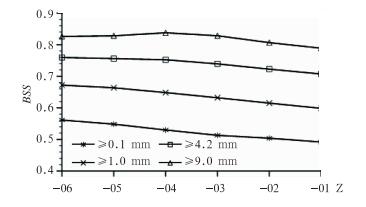
图 7为不同量级以上降水的BSS评分，其值都大于0，说明概率预报有意义，并且随着降水量级的增大，BSS值显著增大；无论降水量级如何，起报时间越晚，BSS值越小。从BSS值发现集合概率预报对暴雨量级的降水预报效果相对其他量级较好，这与Li等(2011)、李俊等(2010)对降水概率预报的BSS检验结果一致，由于BSS评分对事件发生的气候频率比较敏感：事件发生的越稀少, 就越容易得到一个好的BSS评分(涂锴等，2010)。此外，从BS和BSS评分的计算方法出发得到，本文中实况未发生(即o_i为0)，而预报出现不同程度的概率预报的个例较多，由于小(大)降水量级的预报概率相对偏大(小)，使得BS值偏大(小)，对应BSS值偏小(大)，这与前面所得到的小(大)降水量级出现空报的可能性相对较大(小)的结论一致。因此，从BSS评分表明概率预报优于集合平均预报，且随降水量级的增大而更具有应用价值。

3.3.2 Roc检验

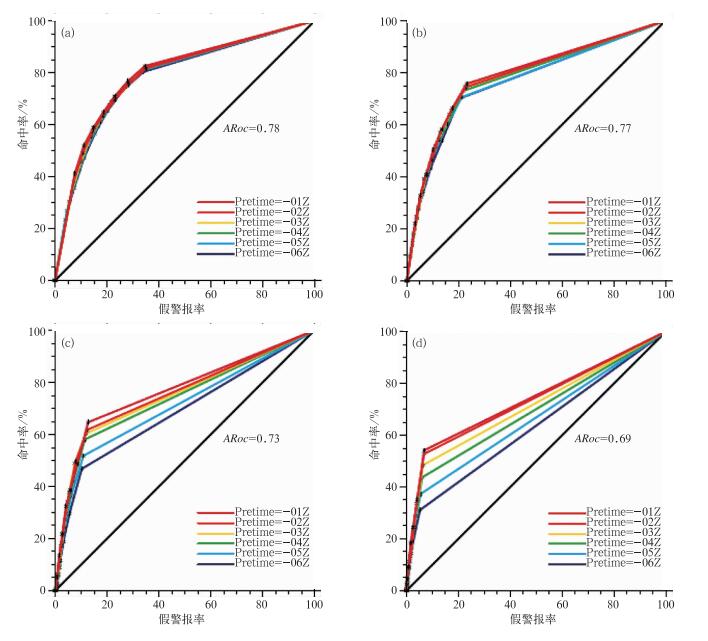
采用Roc曲线检验不同量级以上降水概率预报对于天气事件的分辨能力，其原理是将信号探测理论应用到数值预报的二分类要素预报的检验方法中(Stensrud et al, 1997)。如果Roc面积(ARoc)等于1时，认为集合完美，当ARoc大于0.5时，即当Roc曲线位于对角线上方时为有技巧预报，否则即无技巧。检验发现(图 8)无论降水量级如何，ARoc都大于0.5，呈现越接近预报时间，技巧越高的现象, 并且量级越小，不同起报时间之间的差异越小，说明对于小量级的降水可以提前6 h进行预报；小量级的降水，命中率相对假警报率的散点分布相对均匀，而较大量级的点主要集中在左下角；针对不同降水量级，将所有起报时刻的ARoc做算术平均，发现所有量级的ARoc都在0.65以上，其中≥0.1 mm·h^-1的ARoc最大，为0.78，而≥9.0 mm·h^-1的ARoc相对较小。从Roc检验说明此集合系统能够识别具体的天气事件，同时相对于小量级的降水预报更为准确。

3.3.4 不同概率预报的可用性

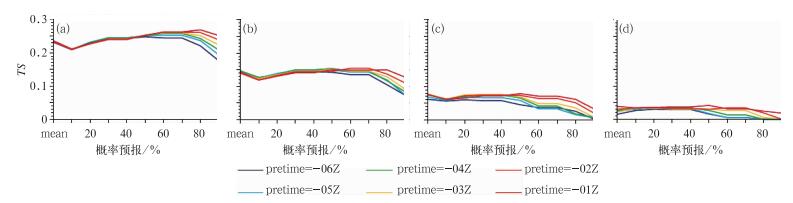
为了进一步了解不同量级以上，不同概率降水预报的可用性，假设预报概率达到10%, 20%, …, 90%时将会发生降水，分别检验小雨、中雨、大雨、暴雨以上不同概率等级的预报评分。图 9为集合平均预报和9个概率等级预报的TS预报评分，得到的结果如下：(1)TS评分随着降水量级增大而减小，其中大、暴雨以上之间的差距较小；(2) 小雨以上降水(图 9a)，不同时间起报的预报技巧随着概率等级的增大差异增大，到大概率等级时，起报时间越晚技巧越高，其中在概率80%时，起报时刻为-01 Z预报技巧最高，而小概率等级时，起报时间越早技巧越高，但是不同时间起报的预报技巧差异不明显；中雨以上降水(图 9b)也有相似的结论，只是小概率等级时，不同时间起报的预报技巧差异比小雨以上的明显；大、暴雨以上量级时无论概率等级如何都是起报时间越晚预报技巧相对越高，此外不同于小量级以上降水，反而概率等级较低时预报技巧相对较高，尤其是暴雨以上量级，当概率等级≥60%时，起报时间较早的预报技巧已接近零；(3) 小雨以上的降水预报，集合平均预报效果略好于小概率等级及较早时刻起报的概率等级为90%的预报。随着降水量级的增大，集合平均与概率等级预报效果最好之间的差异减小。

综合不同概率等级预报的TS评分，小、中雨以上的降水，一般起报时间越晚，预报概率较大时，其可用性较大，而大、暴雨以上的降水，一般起报时间越晚，预报概率较小时，可用性较大。可用性较大的概率预报对应的TS评分一般高于集合平均预报的TS评分，尤其是小、中雨以上的降水量级。此外，从BSS评分、Roc检验也说明，合理前提下，集合概率预报产品具有较高参考价值。

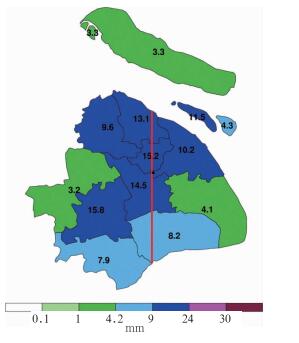
3.4 个例分析

为了直观地体现概率预报的预报效果，用一次短时强降水个例说明。2011年6月17—19日，上海地区出现入梅后最强降雨过程，高、低空大气环流形势，属于典型梅雨的系统配置。高空500 hPa的等高线比较平直，上海正处于东亚浅槽的前部，受偏西气流控制，850 hPa低空切变线横穿上海中北部地区，低空西南风急流带来充沛的水汽，使得低空975 hPa到高空500 hPa，上海地区的相对湿度都达到90%以上。由于东移切变线影响，全市多次出现短时强降水，1 h降水可达到暴雨甚至大暴雨的量级，此外大多数自动站均观测到48 h累计降水80 mm以上，最高出现了210 mm，上海气象局期间多次发布暴雨橙色或黄色预警。从中选取18日12—19时的一次短时强降水过程进行分析，降水量主要集中在13、14、16时，其中14时最大(见图 10)，上海大部分地区出现暴雨量级的降水，图 10中南北线贯穿奉贤(a14)、闵行(a8)、中心城区(a6)、宝山(a1)4个区，线上黑点代表徐家汇，4个地区都出现了大雨及以上的量级。

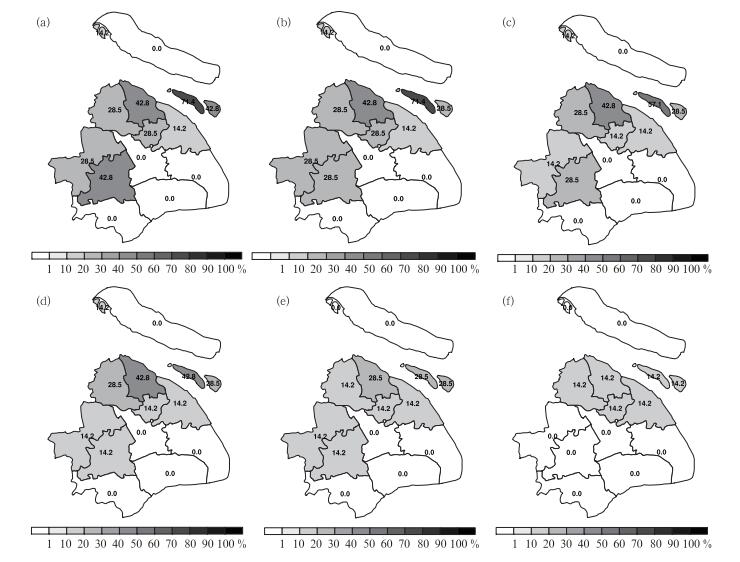
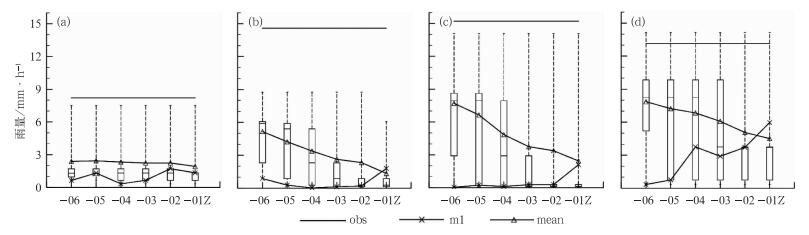
图 11为不同起报时刻，对于暴雨以上量级的降水概率预报，从图中可见，基本上所有起报时刻上海北部都有小概率显示，而从检验可知对于暴雨以上量级的降水概率预报，小概率预报具有较大的可用性，此例中小概率预报出暴雨的情况与实况吻合度较高，只有青浦(a11) 在起报时刻为-06Z至-02Z时实况未出现强降水，对闵行(a8) 地区所有起报时刻都出现了暴雨漏报，其余地区与实况吻合度较好，而且整体的强降水分布也基本与实况一致。图 12为图 10中南北线所经过的4个区的集合成员m1和集合平均对于14时的1 h累计降水预报的时间序列图以及所有集合成员的箱线图。从箱线图可见，集合成员对此次降水的预报差异较大，如中心城区(图 12c)与宝山(图 12d)实况为暴雨，箱线图最大降水量已达到暴雨的量级，所以在图 11暴雨以上的降水概率预报中有小概率显示，而闵行(图 12b)箱线图最大降水量未达到暴雨的量级而出现漏报。集合平均和集合成员m1在此个例中均未达到大或暴雨以上的量级，可能会忽视此次强降水过程，但是相对集合成员m1，集合平均的预报相对较好，尤其是起报时间越早，集合平均预报越接近实况，而集合成员m1却相反，这是由于个别成员对此次降水的预报较好引起的。此例说明若按照就近原则，单一的确定性预报即集合成员m1就无法报出大片的强降水地区，导致漏报，这充分体现了集合预报的指导意义，同时当出现大雨及以上的降水量级时，模式趋向于报弱，但是仍有部分成员扑捉到了大量级降水的信息，而单纯依靠集合平均可能会削弱此次降水强度，说明在进行集合平均预报时要重视概率预报尤其是大量级降水的小概率信息。

4 小结与讨论

本文基于华东区域中尺度快速同化更新数值预报模式系统SMB-WARR，应用时间滞后法进行上海地区精细化短时临近集合预报试验。采用该集合预报系统对2011年6月17日至9月30日期间的降水进行逐小时预报，针对上海地区的面雨量预报进行了检验，结果如下：

(1) 小-大雨量级，集合平均TS评分高于所有集合成员，但暴雨量级集合平均TS评分低于部分集合成员。降水量级越小空报的可能性更大；但总体而言模式预报更偏向于漏报，或者说强度报弱。不同的降水量级，并非都是最接近预报时刻技巧最高，小-大雨量级的TS评分随起报时刻的变化浮动较小，预示着可以提前6 h预报。

(2) 从Talagrand图分析，集合预报系统有一定的降水预报效果，但是离散度还不够理想。

(3) 概率预报优于集合平均预报，具有很好的指示作用。可关注最接近预报时刻，小-中雨以上的降水，预报概率较大时，其可用性较大，而大、暴雨以上的降水，预报概率较小时，可用性较大，此外BSS评分说明概率预报对暴雨以上量级的降水应用价值更大，同时Roc检验说明此集合系统能够识别具体的天气事件。

(4) 本文中大雨及以上的样本较少，可能会对检验结果产生一定的影响，需在今后的研究中尽可能增加样本，使检验结果更具代表性。

(5) 本文只采用等权集合平均来分析集合预报的好坏，未考虑不同集合成员间的预报技巧的高低，此外，权重如何优化选择，待下一步研究试验。