2. 成都高原气象研究所,成都 610072
2. Chengdu Institute of Plateau Meteorology, CMA, Chengdu 610072
数值预报已成为当今天气预报不可或缺的技术支撑。模式初值、动力框架和参数化方案是模式的主要组成部分。众所周知,大气运动具有非线性特性,数值预报其实质是一个典型的初值问题。因此,模式初值对结果具有举足轻重的作用。模式初值场是通过特定的同化方法,把观测资料融合于规则分布的格点而得到。好的同化方法,不但可以更多地利用实测资料,还能很好地抑制“噪声”,尽量多地保留有意义的波动。早期,模式初值场主要采用逐步订正特别是最优插值法同化得到,最近10余年,一种新的资料同化技术——变分同化在气象领域得到迅速发展和广泛应用。研究和实践表明(张华等,2004;丁伟钰等,2005;2006;梁科等,2007;张利红等,2007),经过变分同化的模式初值质量都有不同程度的提高;动力框架是数值预报模式的核心,一个模式所采用方程组、对大气的假设等决定了这个模式的性质和模式的适用范围,也是此模式区别于彼模式的关键所在;物理过程参数化则是为了用模式的有限时空尺度反映“无限”的真实大气运动而采取的权宜之计。真实大气运动的时间尺度可以从数秒到数年,空间尺度可以从分子尺度到行星尺度,物理过程参数化就成为数值模式描写次网格尺度大气物理过程的最佳方式。物理过程参数化可分为大气和下垫面两大类,降水、2 m温度等一些重要的模式预报量就是这些参数化的产物。
GRAPES是我国自主研发的数值模式,模式一直在不断改进和完善,并取得了长足的进步(薛纪善等,2008)。WRF是目前在我国运用比较广泛的一个模式,也得到了用户的好评(宋自福等,2009)。西南地区因其特殊的地理位置和复杂的地形地貌而成为暴雨多发区(李川等,2006;崔春光等,2000;郑庆林等,1997),低值系统、低空急流、冷空气活动是西南地区暴雨形成的关键因子(陶诗言等,2000;陈静等,2003;汪丽等,2004),其中,高原涡、西南涡、切变线和低槽是影响西南地区降水的主要低值系统(陈永仁等,2013;杜倩等,2013)。特殊的地形以及低值系统的复杂、多变使得西南地区成为数值模式预报的“高难度区”(肖玉华等,2010)。模式预报产品是模式各部分、各环节共同作用的产物。针对模式预报结果的检验(肖玉华等,2009;李俊等,2010),可以反映模式的总体性能,但比较笼统,不够明确,也难于区别问题的来源和性质,不能够向模式研发者提供明确的改进方向信息。本文通过模式在西南地区的预报与实测值的均方根误差随时效的演变,以及模式对分类天气过程中低值系统及其强降水预报的检验分析,力图揭示模式在西南地区的初值质量、动力框架性能和降水参数化效果。结论一方面能为完善、改进模式提供有针对性的信息,另一方面也能为预报员针对不同天气过程权重性使用模式提供参考。
1 受检模式和检验方法简介GRAPES(Global/Regional Assimilation and Prediction Enhanced System)是我国自行研制的数值预报模式。模式采用非静力学方程、高度地形追随坐标、半隐式半拉格朗日时间差分方案和Arakawa-C类水平格点分布。三维变分同化以T639 12 h时效预报资料为背景场,同化了探空资料。积云对流参数化采用FCH80方案,边界层采用MRF参数化方案。FCH80方案区别于其他积云对流参数化方案的特点在于描述了积云过程对环境场的反馈作用(薛纪善等,2008)。MRF边界层方案相比于传统的局地K方法而言,弥补了后者不能很好地处理“反梯度通量”的缺陷,因此能在非稳定状态下使用。
WRF(Weather Research and Forecast)是由美国NCAR、NCEP和FSL/NOAA等多家研究部门和大学联合开发的新一代中尺度数值模式。模式采用全可压、非静力学方程,欧拉高度坐标和欧拉质量坐标体系、Arakawa-C类水平格点分布。三维变分同化以NCEP 12 h时效预报资料为背景场,同化探空、地面、自动站、GPS水汽资料获得初值场。积云对流参数化采用GD方案(Grell et al, 2002),边界层参数化采用YSU方案(Noh et al, 2003)。GD方案是Devenyid、Grell在原有A-S质量通量类型方案基础上,引入集成积云方案而成。GD方案在每个格点运行多种积云方案和变量,再将结果平均反馈到模式中。YSU方案是MRF方案的一种改进,它在热量和动量廓线中加入由卷挟造成的热量输送,同时考虑了动量的非局地混合。
对GRAPES和WRF模式在西南地区做出的高度、温度和风的初始分析及间隔12 h的48 h时效预报进行了客观检验,就模式的低值系统预报进行了主观分析,对24 h降水预报进行了主客观检验。虽然模式初始分析场不一定完全等同于模式初值场,二者之间通常还要经过空间插值和物理变换,但无本质区别,模式初始分析场的误差水平可以很大程度反映模式初值场的质量。主客观检验均以实测资料为检验参考,一方面资料纯粹,不包含模式信息,另一方面使用统一检验标准,便于客观地在不同模式间比较。西南地区500 hPa上有17个探空站资料,到850 hPa只有5个站资料,故高空要素分析只针对500 hPa。
客观检验针对西南地区高度场、温度场和风场预报计算了平均均方根误差,针对四川区域降水预报计算了平均TS评分,其公式如下所示:
| $ \begin{array}{l} \overline {RMSE} = \frac{1}{M}\sum\limits_{i = 1}^M {\sqrt {\frac{1}{N}\sum\limits_{j = 1}^N {{{\left( {{F_{i,j}} - {O_{i,j}}} \right)}^2}} } } \\ \;\;\;\;\;\;\;\;\;\;\;i = 1,2, \ldots ,M,{\rm{ }}j = 1,2, \ldots ,N \end{array} $ | (1) |
| $ \begin{array}{l} \overline {TS\left( g \right)} = \frac{1}{M}\sum\limits_{i = 1}^M {\frac{{N{C_i}\left( g \right)}}{{N{C_i}\left( g \right) + N{F_i}\left( g \right) + N{M_i}\left( g \right)}}} \\ \;\;\;\;\;\;\;\;\;\;g = \rm{小雨}, \rm{中雨},\ldots ,\rm{大暴雨} \end{array} $ | (2) |
式(1) 中,RMSE为平均均方根误差,M为统计样本数,在本文为5—9月每天2次(08和20时起报)的实有预报次数,N为探空站数。F为双线性插值到站点的模式预报量,在本文分别取高度、温度、风速和风向,O为对应要素探空实测量。式(2) 中,
低值系统的主观检验按照模式预报系统的位置,分为正确、偏差和错误三级:
正确:预报与实况一致;
偏差:正确预报出系统,但位置偏差在0.5~2.5个经、纬距;
错误:漏报系统或位置误差超过2.5个经纬距。
降水主观检验分析模式降水预报的雨区形态、落区等性能。
2 天气过程分类本文根据降水强度和范围,从2011年发生在四川省境内的降水中筛选出22天强降水过程,按500 hPa上中尺度低值系统不同,将这22天强降水过程分为低槽、低涡和切变三类,如表 1所示,低槽类和切变类过程比较多,占过程总数的86%,表现为低值系统单一,500 hPa上影响系统主要为低槽或切变两类,低涡类则不然,影响系统比较复杂,500 hPa上可能同时出现低涡、低槽、切变3种影响系统,但该类过程出现的几率少,2011年共计出现3次。
|
|
表 1 分类天气过程 Table 1 Classified weather process |
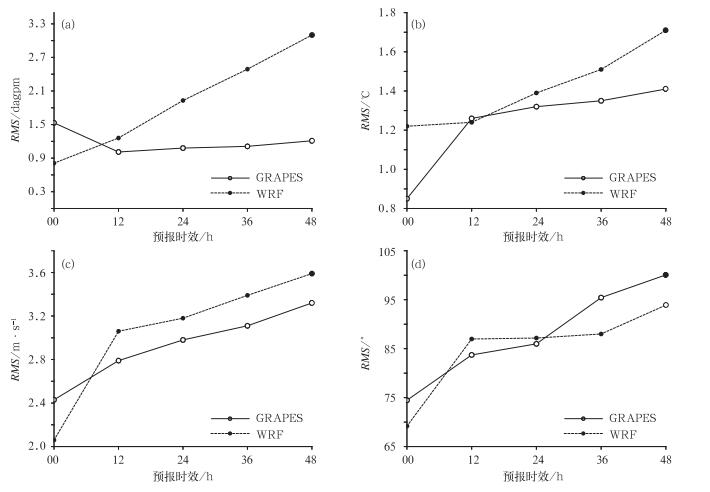
图 1是2011年5—9月500 hPa高度、温度、风速、风向平均均方根误差随预报时效演变。图中曲线显示,四个要素的初始分析均方根误差,GRAPES除温度大于WRF外,其余三个都小于WRF。温度场初始分析平均均方根误差(图 1b),GRAPES为1.22,WRF为0.85,GRAPES高于WRF,而高度、风速和风向的初始分析平均均方根误差,GRAPES分别比WRF小0.72 dagpm,0.37 m·s-1,5.28°。如果以初始分析场均方根误差相对较小的要素个数来衡量模式初值质量,GRAPES的初值质量略好于WRF。
|
图 1 均方根误差时效演变 (a)高度, (b)温度, (c)风速, (d)风向 Fig. 1 Evolution of RMSE as valid time (a) height, (b) temperature, (c) wind speed, (d) wind direction |
初值质量不仅与模式同化技术有关,还与所采用背景场有关。计算T639和NCEP在西南地区12 h时效预报的500 hPa高度、温度和风场的均方根误差显示,背景高度场、温度场差别不大,而风场差别较大,尤其是风向。T639的高度和风速均方根误差平均比NCEP大0.05和0.14,而温度、风向均方根误差平均分别比NCEP小0.06和3.06。比较背景场与初始分析场均方根误差可以看出,GRAPES所用背景场的高度、风速均方根误差都相对比较大,但GRAPES这两个要素的初始分析场均方根误差却相对较小,温度背景场均方根误差相对较小,GRAPES温度初始分析场均方根误差却相对较大,WRF高度、温度和风速初始分析质量与背景场也有类似反比关系。只有风向,两个模式的初值质量与背景场呈现正比关系。背景场与初始分析场均方根误差的这些关系说明,模式初值质量的决定性因素不是背景场,而是同化技术。
进入预报阶段,除风向外,GRAPES高度、温度和风速均方根误差随时效增长快于WRF,到12 h时效,GRAPES三个要素的均方根误差都已超过WRF,尤其是高度场(图 1a),GRAPES几乎呈45°斜率线性增长,相反,WRF的500 hPa高度场均方根误差在前12 h还减小了0.52 dagpm,虽然随后有所增加,到48 h时效时均方根误差为1.21,仍低于初始分析误差。GRAPES温度均方根误差(图 1b)从0~48 h,几乎整个过程都大于WRF,且12 h时效后,斜率逐渐增加。风速均方根误差(图 1c)在12 h后,WRF与GRAPES几乎以相同的斜率增加,风向均方根误差(图 1d),24 h前,两个模式交替变换,之后,WRF大于GRAPES。
上述分析表明,GRAPES在西南地区的初值质量总体优于WRF,但模式性能总体低于WRF。随着时效延长,两个模式对高度、温度场的预报差异呈增长趋势,两个模式的风场预报误差随时效呈平行增加态势,即模式间差异基本保持常数。
从两个模式的误差特性看,500 hPa高度场差异最大,风速差异最小。GRAPES高度场正误差的频率在前24 h不超过10%,后24 h则全为负误差,而WRF高度场正误差频率在48%以上,频率随着时效呈阶梯型变化。前12 h,正误差频率下降最为明显,从初始分析的90%下降到12 h时效时的60%,在随后的12 h里,平均误差特性变化很微弱,24~36 h正平均误差频率再次下降10%,随后,从36~48 h,正平均误差频率基本维持在50%左右。西南地区温度预报,两个模式的正误差频率都比较高,在74%以上,尤其是WRF,前24 h时,频率依次从0时的84%、到12时的94%再到24时的96%,在随后的24 h里,频率保持不变,GRAPES的温度预报正误差频率经历了大幅度变化,从0时的87%下降到12时的74%,然后上升,到48 h时效,已与WRF持平。两个模式的风速预报误差特性差异更多地表现为正平均误差频率量值而非演变趋势,两个模式的风速预报正误差频率都随时效增加,且斜率基本相同,只是GRAPES的频率更高。从0~48 h,GRAPES从21%增加到53%,WRF则从5%增加到44%。两个模式的风向正误差频率则呈现随时效频率下降的特征,WRF从初始分析的35%下降到48 h的21%,GRAPES从初始分析的44%,下降到12 h的26%,再逐步回升到48 h的36%。
上述分析表明,GRAPES对西南地区的500 hPa高度场预报呈现系统性偏低,且误差值随时效迅速增大;WRF对西南地区的高度场预报误差较小,48%以上可能会高报(预报大于实况)西南地区高度;两个模式对西南地区500 hPa温度预报平均均方根误差都在2℃以内,预报较实况偏高的概率在74%以上,其中,WRF的误差值更小、高报的概率更高。两个模式的风场预报差别不大,相比之下,GRAEPS误差更大、风速预报为正距平的频率更高。
3.2 分类天气过程对模式500 hPa低值系统预报的主观分析,根据表 1分类,结果列于表 2。表中,00 h代表模式的初始分析场的检验结果,24 h代表模式预报场的检验。
|
|
表 2 分类天气过程主观检验 Table 2 Subjective verification of classified weather process |
表 2显示,两个模式对三类低值系统的初始分析,与前述模式初始分析性能相似。GRAPES对低槽、切变和低涡过程的初始分析正确率分别为73%、92%和83%,三类平均为83%,WRF分别为87%、84%和67%,平均为79%。两个模式对三类低值系统的初始分析正确率表明,GRAPES对低值系统的初值质量总体好于WRF,尤其是低涡过程,GRAPES的正确率比WRF高16个百分点。表中初始分析错误率显示,WRF对三类低值系统的错误率都为0,这意味着WRF不会漏分析低值系统,而GRAPES则不然。进入预报阶段(以24 h时效预报为代表),WRF对三类过程预报正确率都高于GRAPES,尤其是低涡过程,3次低涡过程,WRF有2次预报正确,1次出现偏差,而GRAPES预报正确率为0,有2次错误,1次偏差。由于低涡类过程样本数太小,准确的结论还有待更多样本的证实,但如果以错误率粗略地评估模式三种低值系统预报能力,WRF对切变的预报能力略低于低槽和低涡,而GRAPES对三类低值系统的预报能力从高到底依次是低槽、切变、低涡。
本节的分析再一次表明,GRAPES的初值质量总体好于WRF,但模式性能是一个值得重点关注的部分,尤其是涡旋类过程,模式从83%的初始分析正确率下降到24 h时效的预报0正确率。
虽然大气低值系统都是大气各要素综合作用、运动的结果,但侧重点有所不同。切变的形成与风场关系更为密切,低涡、低槽则更多地与温度、高度场相关。WRF对风场尤其是风向预报的大误差导致其对与风场相关的切变预报能力不足,而GRAPES高度预报的大误差是导致其低涡过程预报能力较低的主要原因之一。
3.3 分类过程个例分析2011年7月2—6日,四川经历了一次强降水天气过程。影响系统先后有:2日20时至3日20时,出现在四川甘孜、红原、巴塘等附近的低涡,4日08时至5日08时,该区域又出现一个小范围切变,5日20时至6日20时,该切变发展成为大范围切变。而9月17日20时至18日20时,低槽再次出现在该地区附近。三种低值系统有4次都经过了四川的红原站,因此,本文对模式在红原站的预报误差(预报—探空)进行了高度—预报时效垂直剖面分析。在下面的描述中,高度、温度、风速和风向分别以绝对值大于2 dagpm、2℃、3 m·s-1、30°算作大误差。因为风向以北风(从北向南)为0°,因此,风向正误差表示预报风向在实况的右边,反之,风向负误差表示预报风向在实况的左边。
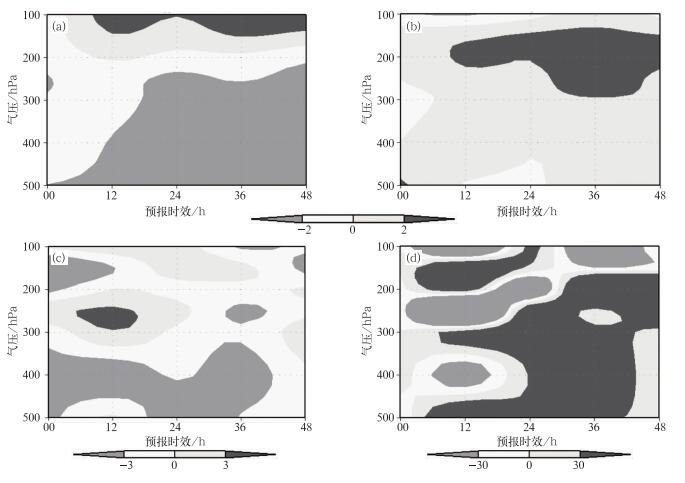
对应低涡阶段,两个模式7月2日00时的12~36 h时效预报误差分析显示,GRAPES的高度、温度和风场预报都出现了较大误差(图 2)。高度大值负误差出现在500~250 hPa。温度大值误差区从12 h起主要出现在300~150 hPa,风速预报表现为负误差,大值区主要分布在500~350 hPa层。风向预报的大误差区随高度呈正负相间分布。WRF的预报误差主要表现在风场,风速以负误差为主,大误差区分布在550~250 hPa之间,风向以正误差为主,6~24 h时效间,大值正误差区分布在500~300 hPa,其上为大值负误差,24 h之后,大值正误差从高层向下传播。
|
图 2 GRAPES 2011年7月2日00时红原站48 h预报误差 (a)高度,(b)温度,(c)风速,(d)风向 Fig. 2 48-h prediction error of GRAPES at Hongyuan Station at 00:00 Z 2 July 2011 (a) height, (b) temperature, (c) wind speed, (d) wind direct |
对应切变阶段,GRAPES的误差主要体现在高度场和风场。高度场大值负误差有随时效从高层向下传播的趋势。风速预报表现为负误差,大值负误差主要分布在500~300 hPa之间,风向误差则有随时效从下向上传播的特点。WRF的大误差仍体现在风场,尤其是风向,为大范围、长时间的大值正误差,只是在12~24 h时效内,在300 hPa层附近出现了小范围的大值负误差。
对第三次切变,两个模式都在200 hPa以上出现大误差。GRAPES 500~300 hPa高度场为大值负误差,风速和风向预报误差表现为随时效正负符号有变化。WRF风速预报主要表现为正误差,分布在300~200 hPa,风向误差则在500~150 hPa之间都为负误差。
对低槽,GRAPES的误差只体现在风速预报,大值正误差出现在250 hPa以上,300 hPa以下主要为负误差。WRF的风速和风向都出现了较大误差。风速大误差有从上向下传播的特点。风向大误差出现在500~400 hPa。
以上分析表明,对低涡的预报,GRAPES的高度、温度和风场都出现较大误差,对切变的预报,GRAPES的误差出现在高度场和风场,对低槽的预报,误差则只体现在风速上。WRF对三种低值系统的预报误差都主要体现在风场。
3.4 降水预报平均TS评分(图略)显示,24、48 h时效各级降水预报都是GRAPES评分不同程度高于WRF。24 h时效,两个模式从小雨到大暴雨预报都获得了评分;48 h时效,只有GRAPES得到了大暴雨评分;两个模式在24 h时效的差异小于48 h时效。24 h时效预报,两个模式的小雨、中雨预报评分相差无几,大雨到大暴雨评分差异有所增加,48 h时效,各个量级的降水评分都大于24 h时效对应量级,WRF还没有得到大暴雨48 h时效评分。
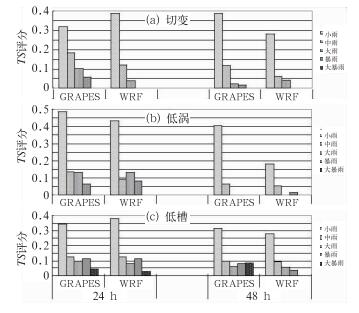
图 3是分类天气过程降水预报平均TS评分。就过程而言,两个模式对低槽的预报评分相对最好。低槽过程(图 3c),从小雨到大暴雨的24 h预报都得到了评分,其中两个模式的暴雨评分还高于大雨评分,到48 h,GRAPES暴雨以下的降水评分有所减小,但大暴雨评分有所增加,WRF也得到了从小雨到暴雨的评分。两个模式在低涡过程的预报中表现相对最差。不仅两个模式两个时效都没有得到大暴雨评分,且预报能力随时效衰减很快,到48 h,GRAPES已失去了对大雨以上降水的预报能力,WRF得到了小雨、中雨和暴雨评分,但分值都不高。两个模式对切变过程的预报能力介于低槽和低涡之间(图 3a),两个模式的预报能力随时效有所衰减,但没有本质的差异,到48 h,两个模式的预报能力与24 h相同,只是分值有不同程度减小。
|
图 3 分类过程降水预报平均TS评分 (a)切变, (b)低涡, (c)低槽 Fig. 3 Average TS score of precipitation forecasts in the classified processes (a) shear, (b) vortex, (c) trough |
就同一模式对三类过程预报而言,GRAPES对低槽过程(图 3c)的预报具有比较明显的优势,不仅从小雨到大暴雨的降水都有不同程度预报能力,且随时效衰减比较小,到48 h模式仍对各级别降水有预报能力。其次是切变过程,GRAPES对切变过程的大暴雨没有预报能力,且预报能力随时效衰减率较大。GRAPES预报能力最弱的是低涡过程,预报能力随时效衰减迅速,到48 h,已没有大雨以上降水的预报能力。WRF对三类过程的预报能力由高到低依次是低槽、低涡、切变。同GRAPES一样,WRF对低槽过程的预报相对最好,但能力衰减率大于GRAPES,到48 h,已失去了对大暴雨的预报能力。WRF对低涡的预报好于对切变的预报。低涡过程WRF得到了24、48 h暴雨预报TS评分,而切变过程,两个时效都没有暴雨以上量级评分。
两个模式对三类过程的降水落区和雨区形态预报(以24 h预报为代表)的主观分析表明,GRAEPS对切变过程的降水强度、落区和形态预报都明显好于WRF。GRAPES对切变过程的24 h时效降水落区预报正确率为67%,而WRF为37.5%,形态预报,GRAPES正确率为56%,WRF为37.5%。低槽过程,GRAPES的强度、落区和形态预报正确率分别比WRF高10%、3%和7%,略具优势。低涡过程,则以WRF优于GRAPES,优势主要体现在强度和形态预报。3次低涡过程,WRF的降水强度、落区、形态预报正确次数分别为3、1和2,而GRAEPS的强度预报全部错误,落区和形态预报各只有一次正确。
综上分析,GRAPES在低槽和切变过程中的强降水预报能力优于WRF,而WRF对低涡过程的强降水预报技高一筹,这一结论与前面所分析模式对分类过程中低值系统的预报能力一致,这表明,两个模式的降水参数化效果没有实质性差异。
4 小结本文以探空站和自动站实测资料为检验参考,通过主客观检验GRAPES和WRF模式在西南地区的初始分析场和预报场,一定程度揭示出模式在西南地区的初值质量、动力框架性能和降水参数化效果。
平均均方根误差分析显示,GRAPES在西南地区高度和风的初值质量略好于WRF,温度初值质量差于WRF。分析显示,模式初值质量的决定因素在于同化技术而非背景场。进入预报阶段,GRAPES高度、温度均方根误差以比WRF更大的斜率随时效增长。两个模式对西南地区高度场的误差特性有实质性区别,GRAPES对西南地区的500 hPa高度场预报呈现系统性偏低,而WRF对西南地区的高度场正误差的概率比较高。温度、风场误差,两个模式的区别只体现在量值上。
分类天气系统主观分析显示,GRAPES对低涡和切变的初始分析质量好于WRF,尤其是低涡,正确率比WRF高出16个百分点,但WRF对三类天气过程的低值系统预报错误率都为0,即WRF不会漏分析低值系统。进入预报阶段,WRF对三类天气过程的低值系统预报正确率都高于GRAPES,尤其是低涡过程。低涡过程成为GRAPES预报性能最低的一类天气过程,WRF预报性能最低的低值系统是切变。单站垂直时间剖面分析显示,GRAPES在低涡过程中,高度、温度和风场预报都出现较大误差,对切变过程的预报,大误差出现在高度场和风场,对低槽预报则只有风速有大误差出现。WRF对三种低值系统的误差都主要体现在风场。
降水预报主客观检验显示,就三类过程而言,两个模式对低槽的预报评分相对最高,低涡过程最低。就模式而言,GRAPES对低槽过程的预报具有比较明显的优势,但对低涡过程的预报能力较低。WRF预报能力相对最高的也是低槽过程,但能力最低的是切变过程,WRF对低涡过程的预报能力高于GRAPES,优势主要体现在降水强度和雨区形态预报。
两个模式对分类天气系统中的低值系统和降水预报性能一致,这说明,两个模式的降水参数化效果水平相当。
陈静, 矫梅燕, 李川, 2003. 青藏高原东侧一次β中尺度对流系统的数值模拟[J]. 高原气象, 22(增刊): 90-101. |
陈永仁, 李跃清, 2013. "12.7.22"四川暴雨的MCS特征及对短时强降雨的影响[J]. 气象, 39(7): 848-860. DOI:10.7519/j.issn.1000-0526.2013.07.006 |
崔春光, 房春花, 胡伯威, 等, 2000. 地形对低涡大暴雨影响的数值模式试验[J]. 气象, 26(8): 14-18. DOI:10.7519/j.issn.1000-0526.2000.08.004 |
丁伟钰, 万齐林, 端义宏, 2005. TRMM降水率资料的三维变分同化及其对"杜鹃"(0313) 台风预报的改进[J]. 大气科学, 29(4): 600-608. |
丁伟钰, 万齐林, 闫敬华, 等, 2006. 对流天气系统自动站雨量资料同化对降雨预报的影响[J]. 大气科学, 30(2): 317-326. |
杜倩, 覃丹宇, 张鹏, 2013. 一次西南低涡造成华南暴雨过程的FY-2卫星观测分析[J]. 气象, 39(7): 821-831. DOI:10.7519/j.issn.1000-0526.2013.07.003 |
李川, 陈静, 何光碧, 2006. 青藏高原东侧陡峭地形对一次强降水天气过程的影响[J]. 高原气象, 25(3): 442-450. |
李俊, 王明欢, 公颖, 等, 2010. AREM短期集合预报系统及其降水预报检验[J]. 暴雨灾害, 29(1): 30-37. |
梁科, 万齐林, 丁伟钰, 等, 2007. 飞机报资料在0506华南致灾暴雨过程模拟中的应用[J]. 热带气象学报, 23(4): 313-325. |
宋自福, 李艳红, 李秋元, 等, 2009. WRF模式对焦作2008年汛期降水的检验[J]. 气象与环境科学, 32(增刊): 23-26. |
陶诗言, 陈联寿, 徐祥德, 等, 2000. 第二次青藏高原大气科学试验理论研究进展(二)[M]. 北京: 气象出版社, 143-149, 368-388.
|
汪丽, 陈静, 李淑君, 2004. "2003.8.28"长江上游特大暴雨的成因分析[J]. 高原气象, 23(增刊): 31-36. |
肖玉华, 何光碧, 陈静, 等, 2009. AREM对2008年西南地区低温雨雪天气预报能力的检验[J]. 暴雨灾害, 28(2): 152-156. |
肖玉华, 赵静, 蒋丽娟, 2010. 数值模式预报性能的地域性特点初步分析[J]. 暴雨灾害, 29(4): 64-69. |
薛纪善, 陈德辉, 等, 2008. 数值预报系统GRAPES的科学设计与应用[M]. 北京: 科学出版社, 331-334, 150-151, 162-165.
|
张华, 丑纪范, 邱崇践, 2004. 西北太平洋威马逊台风结构的卫星观测同化分析[J]. 科学通报, 49(5): 493-498. |
张利红, 沈桐立, 王洪利, 2007. AMSU资料变分同化及在暴雨数值模拟中的应用研究[J]. 高原气象, 26(5): 1004-1012. |
郑庆林, 王必正, 宋青丽, 1997. 青藏高原背风坡地形对西南低涡过程影响的数值试验[J]. 高原气象, 16: 225-234. DOI:10.3321/j.issn:1000-0534.1997.03.001 |
Grell G A, Devenyi D, 2002. A generalized approach to parameterizing convection combining ensemble and data assimilation techniques[J]. Geophys Res Lett, 29(14): 1693. |
Noh Y, Cheon W G, Hong S Y, 2003. Improvement of the K-profile model for the planetary boundary layer based on large eddy simulation data[J]. Boundary-Layer Meteor, 107: 401-427. DOI:10.1023/A:1022146015946 |
 2013, Vol. 39
2013, Vol. 39 