2. 西藏高原大气环境科学研究所,拉萨 850000;
3. 河北省气象科学研究所,石家庄 050021
2. Tibet Plateau Atmospheric Environmental Science Research Institute, Lhasa 850000;
3. Hebei Institute of Meteorological Science, Shijiazhuang 050021
我国旱灾频发,具有范围广、历时长、突发性强、损失大的特点,给我国的粮食生产和粮食安全以及农业的可持续性发展带来了严重威胁(李德等,2012;邵小路等,2013)。开展农业干旱灾害的保险费率厘定研究,对于政府有效应对农业旱灾,开展防灾减灾管理提供技术参考理论依据。
农作物保险风险区划是农业保险工作得以顺利开展的关键前提,也是保险费率厘定的有效支撑(丁少群, 2009; 陈丽, 2010)。美国为农作物保险区分了保险责任区和费率区,分别反映生产力和风险的差异;日本对农作物都会按其风险等级划分,确定相应的保险费率;加拿大农业保险的开展比美国晚20年,根据每个省每个地区的气候、土壤、地理条件和农作物生产历史进行了风险区域划分,不同风险区域内有不同的费率范围。我国很多学者从各个角度出发,对农险区划做了大量研究,也取得了较为满意的成果。庹国柱等(1994)采用指标图重叠法对陕西泾阳棉花生产进行了分区,并根据正态分布原理对所分区域进行了费率厘定。刘长标(2000)分析并研究了农作物区域产量保险风险区划中风险因子的选择问题。邢鹂(2004)运用农作物单产变异系数等指标对我国稻谷、小麦等主要农作物进行了省级风险分区。在此基础上,邢鹂等(2006)增加了粮食的效率指数作为风险区划主导指标,运用聚类分析法对我国粮食产地进行了风险等级划分。2008年邢鹂等针对蔬菜、西瓜的生产风险,提出了针对不同作物的保险组合方式下的分散风险的方法意见(邢鹂等, 2008)。
对于纯保险费率的厘定,传统上运用的方法是参数估计法和非参数估计法(郭晓航, 1993; Turvey et al, 1993; 郭迎春等, 1998; Ker et al, 2000; 王丽红等, 2007; 梁来存, 2010)。鉴于本文的样本数量小,利用非参数法对河北冬麦区冬小麦进行区域产量保险费率厘定,通过基于作物水分亏缺率指数、降水距平百分率指数、抗旱指数以及三个指数构建的干旱风险综合指数分别对纯保险费率进行修正,得到适用于本研究区的费率厘定模型,为我国的农险事业提供理论依据。
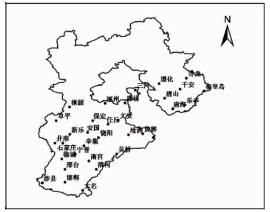
1 资料和方法 1.1 资料来源河北省33个气候站点(图 1)的逐日气象资料(1970—2007年)由河北省气象局提供,其中,作物水分亏缺率指数各因子(吴荣军等, 2013)用到的气象资料见表 1。冬小麦实际单产、水库数量、水库容量、有效灌溉面积、当地农民纯收入、冬小麦播种面积以及冬小麦总产量资料(1993—2005年)来自河北省农村统计年鉴。
|
图 1 河北省冬麦区气象站点的空间分布 Fig. 1 Spatial distribution of selected weather observation stations of winter wheat in Hebei Province |
|
|
表 1 自然水分亏缺率指数各因子用到的气象资料 Table 1 Meteorological data used by factors of natural water deficiency index |
以河北9个地(市)1993—2005年冬小麦平均单产作为参考数据列,记为X0={x0(1), x0(2), x0(3), …, x0(n)};以旱灾风险指数(作物水分亏缺率指数、降水距平百分率指数、抗旱指数) (吴荣军等, 2013)作为比较数据列,记为Xi={xi(k), k=1, 2, …, n }(i=a, b, c), i为旱灾风险指数,a、b和c分别为作物水分亏缺率指数、降水距平百分率指数和抗旱指数,n为参与地(市)的个数(Jiang et al, 2012)。
指数权重的计算公式如下:
(1) 求绝对差序列:
| $ {\Delta _i}\left(k \right) = |{X_0}\left(k \right) - {X_i}\left(k \right)| $ | (1) |
(2) 求两级最小差与最大差
| $ \begin{array}{l} X{\left(k \right)_{{\rm{min}}}} = \mathop {{\rm{min}}}\limits_i (\mathop {{\rm{min}}}\limits_k |{X_0}\left(k \right) - {X_i}\left(k \right)|)\\ X{\left(k \right)_{{\rm{max}}}} = \mathop {{\rm{max}}}\limits_i (\mathop {{\rm{max}}}\limits_k |{X_0}\left(k \right) - {X_i}\left(k \right)|) \end{array} $ | (2) |
(3) 计算关联系数
| $ {\zeta _i}\left(k \right) = \frac{{X{\rm{ }}{{\left(k \right)}_{{\rm{min}}}} + 0.5X{\rm{ }}{{\left(k \right)}_{{\rm{max}}}}}}{{|{X_0}\left(k \right) - {X_i}\left(k \right)| + 0.5X{\rm{ }}{{\left(k \right)}_{{\rm{max}}}}}} $ | (3) |
式中,ζi(k)为各个旱灾风险指数的关联系数。
(4) 求关联度
| $ {r_i} = \frac{1}{n}\sum\limits_{k = 1}^n {{\zeta _i}} \left(k \right)\;\;\;\;\left({k = 1, 2, 3, \cdots, n} \right) $ | (4) |
式中,ri为各个旱灾风险指数的关联度。
(5) 求权重
| $ {\omega _i} = \frac{{{r_i}}}{{\sum\limits_{k = 1}^n {{r_i}} }}\;\;\;\;\left({k = 1, 2, 3, \cdots, n} \right) $ | (5) |
式中,ωi为不同旱灾风险指数的权重。
1.2.2 单个指标的风险区划方法本文采用K-均值聚类法(Jain et al, 1988),克里格插值法(Kriging)插值到0.02°(Cheng, 2013; Li et al, 2013)以及地理信息系统软件绘制分布图,得出各个指标(作物水分亏缺率指数、降水距平百分率指数、抗旱指数以及三者构建的干旱风险综合指数)下的冬小麦干旱风险区划等级,对33个气象站点(冬麦区)进行冬小麦干旱风险评估指标的风险区划。
基于作物水分亏缺率等级及其相应出现概率的函数,构建冬小麦干旱灾害强度风险指数即作物水分亏缺率指数(王素艳等, 2005)。其中,作物水分亏缺率可以描述为冬小麦全生育期本身的需水量与自然供水量的差值占需水量的百分率;基于降水量数据,计算得到各站点的降水距平百分率,在进行等级划分的基础上,确定冬小麦降水距平百分率指数(樊高峰等, 2006; 代立芹等, 2011);采用负指标量化法,基于水库数量、水库容量、有效灌溉面积、当地农民纯收入和冬小麦生产效率等5要素去量纲处理的平均值(李军玲等, 2010),得到抗旱指数,其中,冬小麦生产效率为河北各地(市)冬小麦播种亩产与全国冬小麦亩产的比值。
1.2.3 干旱风险综合指数的计算干旱风险综合指数要综合反映冬小麦干旱灾害强度风险水平、冬小麦减产量与降水负距平的相关性以及各地抗灾能力的强弱,这三者之间既相互独立,又存在一定的相关性,因此选择基于作物水分亏缺率指数、降水距平百分率指数和抗旱指数及其相应的权重,构建河北省冬麦区干旱风险综合指数。公式为:
| $ {B_i} = ({W_i} \times a + {J_i} \times b) \times ({A_i} \times c) $ | (6) |
式中,Wi为作物水分亏缺率指数,Ji为降水距平百分率指数,Ai为抗旱指数,a、b和c依次为3个指数的权重。
1.2.4 趋势产量的计算利用河北省各地(市)1993—2005年的冬小麦单产资料进行分析,选用三次多项式法对趋势产量进行模拟(表 2)。
|
|
表 2 各地市的冬小麦单产趋势方程表 Table 2 Equation form of the winter wheat yield trend in every city |
具体步骤是将给定的13年(1993—2005) 数据分别带入公式,计算各地(市)每年的趋势产量(王春乙, 2010)。
1.2.5 纯保险费率厘定的计算本文以河北省的9个地(市)为基本单位(其中,张家口和承德为冬小麦非种植区),利用各市1993—2005年的冬小麦生产的实际资料,采用非参数法(Ker et al, 2000; 梁来存, 2011)对冬小麦单产保险的纯费率进行厘定。冬小麦单产保险的纯费率公式如下:
| $ R = \frac{{E\left({Loss} \right)}}{{\lambda {{\bar Y}_{it}}}} $ | (7) |
式中,R为冬小麦单产的纯费率,λ为保障制度(λ=100%),Yit为趋势产量[i指地(市), t指年份],则λ Yit 表示投保年份冬小麦单产合同的保障水平,E(Loss)为粮食单产灾损期望值。
其中,本文利用高斯函数来求E(Loss,当且仅当x < λYit时,损失才能成立,公式如下:
| $ \begin{array}{l} E\left({Loss} \right) = \frac{1}{{\sqrt {2\pi } n{h_n}}}\sum\limits_{t = 1}^n {\int_0^{\lambda {{\bar Y}_{it}}} {\left\{ {(\lambda {{\bar Y}_{it}} - x) \times } \right.} } \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{\rm{exp}}\left[ { - \frac{1}{2}{{\left({\frac{{x - {X_{it}}}}{{{h_n}}}} \right)}^2}} \right]} \right\}{\rm{d}}x \end{array} $ | (8) |
式中,n为冬小麦单产的样本容量,hn为带宽,Xit为冬小麦实际单产。
本文采用Silverman的经验法则计算带宽,公式如下:
| $ {{h}_{n}}=0.9\text{min}{\left\{ s,\frac{Q}{1.34} \right\}}/{{{n}^{\frac{1}{5}}}}\; $ | (9) |
式中,s为各市的样本标准差,Q为四分位数间距。其中,样本标准差的公式为:
| $ {s_i} = \sqrt {\frac{{\sum\limits_{t = 1}^n {{{({X_{it}} - \overline {{X_i}})}^2}{S_{it}}} }}{{\sum\limits_{t = 1}^n {{S_{it}}} }}} $ | (10) |
式中,Xit和Sit分别指第i个地(市)第t年的冬小麦实际单产和种植面积;
| $ \overline {{X_i}} = \frac{{\sum\limits_{t = 1}^n {{S_{it}}{X_{it}}} }}{{\sum\limits_{t = 1}^n {{S_{it}}} }} $ | (11) |
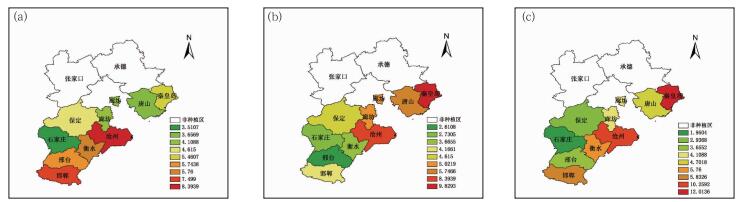
图 2a为河北冬麦区冬小麦全生育期作物水分亏缺率指数的风险区划图,可以看出,由南向北,风险等级逐步递增。图 2b为基于降水距平百分率指数得到的干旱风险区划图,可以看出,由南向北,风险等级逐步递增。图 2c为基于抗旱能力指数的干旱风险区划图,可以看出,由北向南,风险等级逐步递增。

|
图 2 基于不同指数的河北省冬麦区风险区划 (a)作物水分亏缺率指数, (b)降水距平百分率指数, (c)抗旱指数 Fig. 2 Risk zoning based on different indices in Hebei winter wheat region (a) the natural water deficit rate index, (b) the precipitation anomaly percentage index, (c) the drought resistance index |
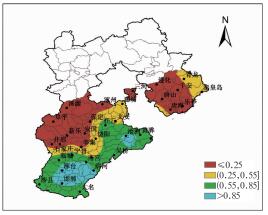
利用灰色关联分析,计算得到作物水分亏缺率指数、降水距平百分率指数和抗旱指数的关联度和权重,详见表 3。基于河北省冬麦区干旱风险综合指标,得到综合风险区划图(图 3)。可以看出,河北省由北向南,冬小麦干旱综合风险有逐渐加重的趋势。
|
|
表 3 河北省旱灾风险指数灰色关联分析 Table 3 Drought risk index of gray relational analysis in Hebei Province |
|
图 3 河北冬麦区干旱综合风险区划 Fig. 3 Risk zoning based on the integrated drought risk index |
本文利用Jarque-Bera统计量判断各地(市)单产是否服从正态分布。结果表明,在α=0.01的显著性水平上,各地(市)的粮食单产均服从正态分布。利用表 2计算出各地(市)的趋势单产,结合Matlab-R2009a软件的编程功能计算出2006年河北省9个地(市)的冬小麦单产的期望损失E(loss),最后利用式(7) 求出冬小麦单产保险的纯保险费率水平,见表 4。
|
|
表 4 1993—2005年河北省各地(市)产量纯保险费率 Table 4 The production pure premium rate of Hebei Province in 1993-2005 |
由于河北各地(市)冬小麦的实际保险费率不仅与冬小麦旱灾风险指数有关,还涉及到安全系数、营业费、预定节余率等问题,故通过对纯保险费率的修正得到实际保险费率,公式如下:
| $ \begin{array}{l} {R_i}\% = {R_i} \times \left({1 + 安全系数} \right) \times \left({1 + 营业费用} \right) \times \\ \;\;\;\;\;\;\;\;\;\left({1 + 预定节余率} \right) \times 区域风险系数 \end{array} $ | (12) |
式中,Ri%为各地(市)的修正纯费率,Ri为各地(市)的纯费率,安全系数为15%,营业费用20%,预定节余率5%(庹国柱等, 2005)。
2.3.1 基于单个干旱指数的纯保险费率修正根据河北冬麦区33个气象站点得到的作物水分亏缺率指数、降水距平百分率指数和抗旱指数,求出河北冬小麦种植区石家庄等9个地(市)的对应干旱指数[把同属于各个地(市)的站点的干旱指数求平均],再利用K-均值聚类法将其分别聚类为4个等级,这里假设低风险区的风险系数为1.0,中等风险区为1.4,较高风险区为1.8,高风险区为2.2。本文选取保障水平在100%的纯费率,分别建立了河北省冬麦区的纯保险费率修正图(图 4)。图 4a为河北冬麦区冬小麦全生育期作物水分亏缺率指数修正下的纯保险费率,可以看出,冬小麦保险的修正纯保险费率在河北省区域内呈现中西部地区偏低、南部偏高以及东部地区沧州和秦皇岛高、廊坊和唐山低的分布特点。
|
图 4 基于不同指数的河北省冬麦区纯保险费率修正 (a)作物水分亏缺率指数, (b)降水距平百分率指数, (c)抗旱指数 Fig. 4 Corrected pure premium rate of Hebei winter wheat region based on different indices (a) the natural water deficit rate index, (b) the precipitation anomaly index, (c) the drought resistance index |
图 4b为基于降水距平百分率指数得到的纯保险费率修正图,可以看出,冬小麦保险的修正纯保险费率在河北省区域内呈现由南向北,逐渐递增的分布特点。
图 4c为基于抗旱指数的修正下的纯保险费率图,可以看出,冬小麦保险的纯费率在河北省区域内呈现中西部地区偏低、南部和东部地区偏高的分布特点。
2.3.2 基于干旱综合指标的纯保险费率修正基于河北省冬麦区各地(市)干旱风险综合指标,得到修正后的纯保险费率(图 5)。可以看出,冬小麦保险的纯费率在河北省区域内呈现中西部地区偏低、南部和东部地区偏高的分布特点,这与河北各地(市)风险发生的实际情况基本一致。

|
图 5 基于干旱综合指标的河北省冬麦区纯保险费率修正 Fig. 5 Corrected pure premium rate based on the integrated drought indicators |
综合表 3、图 4和图 5,可以看出,(1) 河北冬麦区各地(市)冬小麦保险的纯保险费率水平差异不大,如:在相同保障水平下,纯费率最低值为石家庄的1.3460%,最高值为秦皇岛的3.7686%;而修正纯费率水平差异显著,尤其是抗旱指数修正下的纯保险费率,在相同保障水平下,修正的纯保险费率最低值与最高值相差10%以上。主要原因是基于抗旱指标的秦皇岛的风险系数极高,拉大了与风险系数极低的石家庄的差距。(2) 秦皇岛的纯保险费率在河北省冬麦区是最高的,而通过干旱综合指标修正后的纯保险费率趋于平均水平;邢台的纯保险费率在河北省冬麦区低于平均水平,而通过干旱综合指标修正后的纯保险费率高于平均水平。究其原因,秦皇岛地处半湿润区,属于温带季风气候,年均降水量在600 mm左右。农业基础设施较好,具有较好的灌溉条件,农业综合抗旱能力较强,使得该地区综合风险系数较低;邢台属于半干旱、半湿润暖温带大陆性季风气候,年均降水量在450 mm左右,冬小麦生长季内降水亏缺,降水变率大,水土流失严重,地下水位连年下降,加上该区生产力水平不高,灌溉潜力有限,致使该区冬小麦综合风险系数较高。
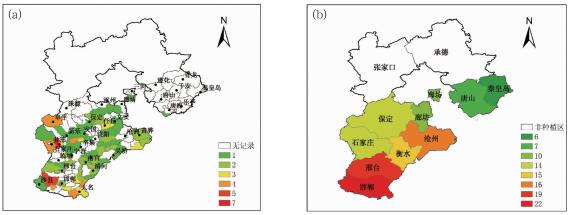
2.4 基于不同干旱指标修正的纯保险费率厘定结果的验证根据温克刚等(2008)编著的《中国气象灾害大典》(河北卷),统计了河北省1949—2000年间发生的县域和地市旱灾频次分布(图 6)。结合图 6,邯郸、邢台、沧州和衡水发生旱灾的频次较多,唐山、秦皇岛发生旱灾的频次偏少,这与图 4a和图 5给出的作物水分亏缺率指数修正下纯保险费率和基于干旱综合风险指标修正下纯保险费率的厘定结果最吻合,从空间尺度上表明了本文提出的作物水分亏缺率指数和构建的干旱综合风险区划模型对于纯保险费率的修正具有一定的应用价值。
|
图 6 河北省冬麦区旱灾频次分布 (a)县域,(b)地(市) Fig. 6 Drought frequency distribution of the winter wheat region in Hebei Province (a) county town, (b) prefecture-level city |
通过分别建立河北冬小麦种植区石家庄等9个地(市)的作物水分亏缺率指数和干旱综合指标与河北省1949—2000年间发生的地市旱灾频次之间的线性回归关系发现,前者决定系数R2=0.3994(P < 0.01),后者决定系数R2=0.5987(P < 0.01),后者较前者回归关系显著。因此,基于作物水分亏缺率、降水距平百分率和抗旱指数构建的干旱综合风险区划模型是最可靠的,河北省冬小麦的纯保险费率可以由冬小麦旱灾综合风险等级来修正。
3 结论本文从冬小麦不同干旱指标下的风险区划的角度出发,对风险等级不同的冬小麦进行有差别的区域产量保险的费率厘定,最后得到适用于本研究区的费率厘定模型,从而实现冬小麦农业保险的持续健康发展。
冬小麦各个干旱指标下修正的纯保险费率结果表明,河北冬麦区全生育期作物水分亏缺率指数区域分布有以下特点:由北向南,修正纯保险费率的厘定逐步递增,这与作物水分亏缺率指数得出的风险区划等级存在偏差,是因为两者的区域范围不一致;降水距平百分类指数区域分布有以下特点:由南向北,修正纯保险费率的厘定逐步递增;抗旱指数区域分布有以下特点:由西向东,修正纯保险费率的厘定逐步递增;河北省由北向南,冬小麦干旱综合指标修正下的纯保险费率有逐渐增加的趋势。通过作物水分亏缺率指数和干旱综合指标分别与河北省冬麦区地市旱灾频次之间的线性回归关系发现,基于作物水分亏缺率、降水距平百分率和抗旱指数构建的干旱综合风险区划模型是最可靠的,河北省冬小麦的纯保险费率可以由冬小麦旱灾综合风险等级来修正。
陈丽, 2010. 国外农业保险风险区划的经验启示[J]. 中国集体经济, (2): 198-199. |
代立芹, 李春强, 魏瑞江, 等, 2011. 河北省冬小麦气候适宜度及其时空变化特征分析[J]. 中国农业气象, 32(3): 399-406. |
丁少群, 2009. 我国农业保险的发展需要风险区划[J]. 中国集体经济(财税金融), (9): 91-92. |
樊高峰, 苗长明, 毛裕定, 2006. 干旱指标及其在浙江省干旱监测分析中的应用[J]. 气象, 32(2): 70-74. DOI:10.7519/j.issn.1000-0526.2006.02.013 |
郭晓航, 1993. 农业保险[M]. 大连: 东北财经大学出版社.
|
郭迎春, 闫宜玲, 王卫, 等, 1998. 农业自然风险评估及区域农业保险费率的确定方法[J]. 应用气象学报, 9(2): 231-238. |
李德, 张学贤, 刘瑞娜, 2012. 冬小麦冬季干旱时段灌溉气象适宜指数研究[J]. 气象, 38(12): 1565-1571. |
李军玲, 刘忠阳, 邹春辉, 2010. 基于GIS的河南省洪涝灾害风险评估与区划研究[J]. 气象, 36(2): 87-92. DOI:10.7519/j.issn.1000-0526.2010.02.013 |
梁来存, 2010. 我国粮食单产保险纯费率厘定的实证研究[J]. 统计研究, 27(5): 67-73. |
梁来存, 2011. 我国粮食保险纯费率厘定方法的比较与选择[J]. 数量经济技术经济研究, (2): 124-134. |
刘长标, 2000. 农作物区域产量保险的精算研究[M]. 北京: 中国人民大学.
|
庹国柱, 丁少群, 1994. 论农作物保险区划及其理论依据--农作物保险区划研究之一[J]. 当代经济科学, (3): 64-70. |
庹国柱, 李军, 2005. 农业保险[M]. 北京: 中国人民大学出版社, 400-401.
|
邵小路, 姚凤梅, 张佳华, 李先华, 2013. 基于蒸散干旱指数的华北地区干旱研究[J]. 气象, 39(9): 1154-1162. DOI:10.7519/j.issn.1000-0526.2013.09.010 |
王春乙. 2010. 中国重大农业气象研究, 6-8.
|
王丽红, 杨华, 田志宏, 2007. 非参数核密度法厘定玉米区域产量保险费率研究--以河北安国市为例[J]. 中国农业大学学报, 12(1): 90-94. |
王素艳, 霍治国, 李世奎, 等, 2005. 北方冬小麦干旱灾损风险区划[J]. 作物学报, 31(3): 267-274. |
温克刚, 臧建升, 2008. 中国气象灾害大典(河北卷)[M]. 北京: 气象出版社, 56-75.
|
吴荣军, 史继清, 关福来, 等, 2013. 干旱综合风险指标的构建及风险区划--以河北省冬麦区为例[J]. 自然灾害学报, 22(1): 145-152. |
邢鹂. 2004. 中国种植业生产风险与政策性农业保险的研究. 南京农业大学博士学位论文, http://cdmd.cnki.com.cn/Article/CDMD-10307-2004086122.htm
|
邢鹂, 高涛, 吕开宇, 等, 2008. 北京市瓜蔬类作物生产风险区划研究[J]. 中国农业资源与区划, 29(6): 55-60. |
邢鹂, 钟甫宁, 2006. 粮食生产与风险区划研究[J]. 农业技术经济, (1): 19-23. |
Cheng Tangpei, 2013. Accelerating universal Kriging interpolation algorithm using CUDA-enabled GPU[J]. Comput Geos, 54: 178-183. DOI:10.1016/j.cageo.2012.11.013 |
Jain A K, Dubes R C.1988.Algorithms for Clustering Data.New Jersey, Prentice-Hall.
|
Jiang Guiqin, Yu Fuliang, Zhao Yong, 2012. An analysis of vulnerability to agricultural drought in China using the expand grey relation analysis method[J]. Procedia Engineering, 28: 670-676. DOI:10.1016/j.proeng.2012.01.789 |
Ker A P, Goodwin B K, 2000. Nonparametric estimation of crop insurance rates revisited[J]. Am J Agr Eco, 8(3): 463-478. |
Li Fangyi, Luo Zhen, Rong Jianhua, et al, 2013. Interval multi-objective optimisation of structures using adaptive Kriging approximations[J]. Computers & Structures, 119: 68-84. |
Turvey C G, Zhao C, 1993. Parametric and nonparametric crop yield distributions and their effects on all-risk crop insurance premiums[M].
Guelph: University of Guelph.
|
 2013, Vol. 39
2013, Vol. 39 