2. 沈阳军区空军气象中心,沈阳 110015;
3. 辽宁省人工影响天气办公室,沈阳 110016
2. Air Force Meteorological Centre of Shenyang Military Region, Shenyang 110015;
3. Weather Modification Office of Liaoning Province, Shenyang 110016
雷暴是一种灾害性天气,其生命史短、空间尺度较小、具有局地性特征,一直是天气预报重难点之一。如何提高雷暴预报的准确率,加强对雷暴天气的分析与研究,对防雷减灾工作至关重要。
目前在国内利用探空因子进行雷暴预报的研究中,多采取多元统计回归的方法。这种方法不可避免的问题就是雷暴发生的非线性与线性回归算法之间的矛盾,因此需要大力发展非线性算法。Agostinon(2005)利用探空资料和闪电定位资料对神经网络进行训练,并对雷暴的发生以及闪电密度进行了预报。赵旭寰等(2009)尝试利用神经网络法对南京地区雷暴天气进行预报。这些研究表明,神经网络预报雷暴发生是可行的。但由于研究重点和地域的不同,网络的构建方式存在一定差异,预报结果判定方式也存在一定可变性。因此,如何解决上述问题,合理构建和使用网络,从而达到更好的预报效果,具有十分重要的意义。
通过对雷暴发生的影响因子进行分析计算,从中发掘有用的预报信息作为模型输入,尝试采用双隐藏层BP网络及两级分类的输出,对预报因子归一化处理,试图寻找泛化能力最优的网络来进行雷暴预报的建模研究,以期获得更高的预报准确率和更可靠的预报结果判定方式。
1 资料介绍及处理 1.1 资料选取选用2007—2008年太原站(37.78°N、112.55°E)的探空资料和山西省闪电定位资料。太原站每天进行两次探空,获取探空资料时间为北京时间08和20时,给出每天两次大气状况。闪电定位资料由山西省气象局提供。为了对网络进行训练及验证,将2007年的数据作为训练样本,2008年的数据作为独立检验样本,采用探空因子作为输入矩阵,雷暴发生与否作为输出矩阵。
1.2 预报量的处理据统计,太原雷暴天气多发生于夏季,闪电定位系统探测到的地闪有70%发生在6—8月,因此本文将研究时间限定到6—8月里。
雷暴的发生是小概率事件,为提高预报量序列中雷暴的发生概率,以太原站为中心,50 km为半径圆周范围,若探空后12 h内,闪电定位网探测到1或1次以上且电流强度在10~100 kA的闪电过程,则认为太原站发生雷暴。
至此,除去缺失资料的样本,网络训练样本对为179个,其中有闪电记录的为84个,雷暴样本概率为46.9%。这里将以这179个样本对作为训练样本,进行BP神经网络的建模研究。
1.3 预报因子的选取雷暴发生、发展的基本条件有环流条件、水汽条件、不稳定条件及抬升条件。国内外许多学者研究认为,闪电活动与大气不稳定参数存在一定的相关性(郑栋等,2005)。探空因子备选集采用美国怀俄明州立大学提供的探空资料指数产品,共计20个。其中对流有效位能CAPE、虚温计算的CAPE、对流抑制指数CIN、虚温计算的CIN、粗里查森数BRN、虚温计算的BRN、500~1000 hPa厚度7个指数由于样本数不全舍弃,虚温计算的LI与LI对比分析舍弃虚温计算的LI。至此本文保留了12个预报因子,具体定义见表 1。为选择合适的预报因子作为输入,首先分别将这12个因子与预报量作相关性分析。
|
|
表 1 预报因子及其定义 Table 1 The predictors and their definition |
由于对流参数物理量是连续型因子,雷暴发生与否为0, 1变量,所以不直接求出其相关系数,而是求出其点双序列相关系数。具体而言,当X是连续型因子,Y是0, 1变量,它们之间的相关系数为:
| $r = \frac{{{{\bar x}_{\left( 1 \right)}} - \bar x}}{{{S_x}}}{\left( {\frac{P}{{1 - P}}} \right)^{\frac{1}{2}}}$ | (1) |
式中,x为因子x的平均值,x(1)为在y=1时x的平均值,P为事件y=1出现的频率,Sx为因子的样本标准差(刘震钊等,2010)。
本文选取相关系数在0.3以上的7个指数作为预报因子,分别是CT指数、K指数、抬升指数、累积可降水量、沙氏指数、强天气威胁指数和TT指数。
其中K指数在考虑了大气层结不稳定的同时,还考虑了对流层中层的水汽条件。CT指数、TT指数表征了雷暴发生前的大气层结的不稳定条件。抬升指数LI表征大气不稳定度,当LI<0时,大气层结不稳定,且负值越大,不稳定程度越大,反之,则表示大气层是稳定的。沙氏指数SI和强天气威胁指数SWI属于稳定度指标。累积可降水量PWFES代表水汽指标。
2 神经网络的构建人工神经网络(Artificial Neural Network,ANN)是理论化的人脑神经网络的数学模型,是基于模仿大脑神经网络结构和功能而建立的一种信息处理系统。它实际上是由大量简单原件相互连接而成的复杂网络,具有高度的非线性,能够进行复杂的逻辑操作和非线性关系实现的系统(袁曾任,1999)。
在人工神经网络的实际应用中,应用最广泛的就是BP网络模型,它体现了人工神经网络最精华的部分。近年来BP神经网络也越来越多的应用于大气科学领域(刘旸等,2011;官莉等,2010;张雪慧等,2009;农孟松等,2011;程炳岩等,2011),这种网络模型相对于其他模型而言,通用性好,且较为成熟。相对传统的数理统计方法而言,BP神经网络可以求解非线性问题,同样对样本大小的要求也可以相对少得多,BP网络模型示意图,如图 1所示。

|
图 1 双隐层BP网络模型 Fig. 1 The double hidden layer BP network model |
BP网络可有效地用于复杂的非线性函数的逼近,一个3层的前馈网络能够实现任意精度的连续函数映射(丛爽,2003),两个隐层的神经网络则可以解决各种分类问题(金龙,2004)。因此本文尝试构建两个隐藏层的BP网络。
2.1 输入输出数据的处理训练样本集是影响BP网络性能优劣关键。神经网络是以样本在事件中的统计几率来进行训练和预测的。归一化是归纳统一样本的统计分布性,可以简化计算,缩小量值,加快网络的收敛。归一化在[0,1]之间是统计的概率分布,归一化在[-1,+1]之间是统计的坐标分布。兼顾sigmod函数的定义,这里采取式(2) 对输入样本进行[0.1, 0.9]之间的归一化:
| $\mathit{\boldsymbol{X = }}0.1 + 0.8\left[ {\left( {\mathit{\boldsymbol{P}} - \min \mathit{\boldsymbol{P}}} \right)/\left( {\max \mathit{\boldsymbol{P}} - \min \mathit{\boldsymbol{P}}} \right)} \right]$ | (2) |
这里,P表示归一化前的输入数据,minP表示矩阵P的最小值,maxP表示矩阵P的最大值,X表示归一化之后的输入矩阵。
需要说明的是,训练前,2007年的数据进行归一化;仿真前,2008年的样本要采取与2007年同样的设置来归一化。
对于输出矩阵,在12 h内发生一次雷暴即认为该时段有雷暴发生。输出矩阵按雷暴的发生与否分成两类,并考虑到sigmod函数的输出范围,无雷暴设计成[0.1,0.9],有雷暴设计成[0.9,0.1]。
2.2 学习算法在选择算法对网络进行训练的时候,在网络参数很多,需要考虑存储容量问题时,选择共轭梯度法。经试验,这里选择Scaled共轭梯度法trainscg。
2.3 传递函数各层神经元的传递函数根据需要,不同层内采取不同的传递函数组合。并且一般常采用S形函数和线性函数组合。S形函数能将跨度很大的数值压缩到一个很小的固定范围内。输出层常采用线性函数,这样整个网络的输出可以取实数域内任何值。双隐层的网络结构,需要3层传递函数,选取tansig和purelin的结合,在试验中,最终确定tansig-tansig-purelin组合。这两种函数的表达式如下:
| $\mathit{\boldsymbol{A}} = f\left( {\mathit{\boldsymbol{W}} \cdot \mathit{\boldsymbol{P}} + b} \right) = \frac{1}{{1 + {{\rm{e}}^{ - \left( {\mathit{\boldsymbol{W}} \cdot \mathit{\boldsymbol{P}} + b} \right)}}}}$ | (3) |
| $\mathit{\boldsymbol{A}} = f\left( {\mathit{\boldsymbol{W}} \cdot \mathit{\boldsymbol{P}} + b} \right) = \mathit{\boldsymbol{W}} \cdot \mathit{\boldsymbol{P}} + b$ | (4) |
其中,P表示输入矩阵,W表示权值矩阵,b表示偏置矩阵,A表示输出。
2.4 过拟合问题的处理怎样寻求泛化能力最大的网络,是网络构建的一个难题。网络的泛化性能是指神经网络对训练样本以外的新样本的适应能力。在网络的训练过程中经常会出现过拟合现象,即在网络训练过程中,从某一次训练开始,随着网络的训练能力提高,仿真的能力反而下降。解决这个问题的一种办法是:在数据输入中,给训练的数据分类,分为正常训练用、变量数据和测试数据,3种数据分别占用全部样本的0.6、0.2和0.2。设定参数maxfail=10(最大失败次数),在网络训练的过程中,如果从某一步开始,变量数据的误差不降反升,则Validation Checks开始计数,当计数到10,则认为网络陷入过拟合,停止训练。
2.5 隐节点数的选取目前隐节点的选取没有一个固定的参照,主要靠经验试凑。
| $h = \sqrt {n + m + a} $ | (5) |
其中,h为隐节点数,n为输入节点数,m为输出节点数,a为1~10之间的常数。
隐节点数h与输入节点n的关系为:
| $h = {\log _2}n$ | (6) |
在神经网络研究中,高大启(1998)用曲面对隐节点数的规律进行拟合,由最小二乘法得到拟合公式为:
| $\begin{array}{l} h = \sqrt {0.43mn + 0.12{m^2} + 2.54n + 0.77m + 0.35} \\ \quad \quad + 0.51 \end{array}$ | (7) |
隐节点数太少会造成信息不足,造成网络训练达不到要求;太多会造成浪费,使训练时间加长。
由于这些公式只是大致给出了隐节点的取值范围,而不同的研究问题之间有很大的差别,所以仅根据上述公式来确定隐节点数不是十分合适。这里将其作为参考,尝试多种隐节点数组合,根据网络训练的MSE,最终确定两层隐节点数分别为3和9(详见表 2)。
|
|
表 2 隐节点的选取 Table 2 Selecting hidden nodes |
选用2008年6—8月的167个样本作为独立样本进行预报检验,其中雷暴样本69个,非雷暴样本98个,预报结果见表 3。预报结果令人满意,表明此神经网络模型适用于太原市雷暴预报。
|
|
表 3 2008年6—8月167个独立样本预报结果 Table 3 Forecasting results with the 167 independent samples from June to August 2008 |
采用TS评分和准确率来检验预报结果:
| $TS = \frac{a}{{a + b + c}} = \frac{{60}}{{60 + 17 + 9}} = 69.77\% $ | (8) |
| $准确率 = \frac{{a + d}}{{a + b + c + d}} = \frac{{60 + 81}}{{167}} = 84.43\% $ | (9) |
为对比分析双隐层BP网络在预报雷暴问题上的优势,使用同样的训练样本和独立检验样本,分别采用单隐层BP网络、多元线性回归算法及最优线性回归算法进行预报。
(1) 采用单隐层BP网络算法预报结果:在167个独立检验样本中,雷暴样本报对62次,非雷暴样本报对68次,漏报7次,空报30次。其TS评分为62.63%,准确率为77.84%。
(2) 采用多元线性回归算法进行预报建模,得到如下回归方程:
| $\begin{array}{l} Y = - 3.6870 - 0.0284CT + 0.0089KI - \\ \quad \quad 0.0196LI + 0.0268PWFES + \\ \quad \quad 0.0925SI + 0.0011SWI + \\ \quad \quad 0.0765TT \end{array}$ | (10) |
雷暴样本报对56次,非雷暴样本报对76次,漏报13次,空报22次。其TS评分为61.54%,准确率为79.04%。
(3) 采用最优线性回归算法进行预报建模试验。采用一种逐步回归方法求得的局部最优子集来取代全局最优子集,经过计算,选取了5个因子。因子选取方法取自李东风等(2008)的研究结果,得到如下回归方程:
| $\begin{array}{l} Y = 6.9764 + 0.0059CT + 0.0041KI - \\ \quad \quad 0.0653LI - 0.0297MMLPT - \\ \quad \quad 0.0207SWI \end{array}$ | (11) |
雷暴样本报对55次,非雷暴样本报对78次,漏报14次,空报20次。其TS评分为61.8%,准确率为79.64%。
3.3 预报结果对比分析为了说明双隐层BP网络预报在雷暴上的优势,以雷暴样本为例,将网络的两级输出绘图,如图 2所示。若实心圆点数值大于空心圆点,即该样本是雷暴的可能性大于非雷暴,则认为是雷暴样本;反之是非雷暴样本。相较于线性回归算法,这种方法的优势在于不需要设定阈值,结果更可靠。

|
图 2 双隐层网络实际输出数值特征 Fig. 2 Statistical characters of actual output from double hidden layer BP network |
图 3给出了双隐层BP网络与多元线性回归算法69个雷暴样本的输出对比图。由图 3可以看出,多元线性回归法的概率值比较分散,双隐层BP网络法的输出结果大部分都集中在[0.8,1]区间内,更加接近真值。

|
图 3 BP网络法与多元线性回归法预报结果对比 Fig. 3 Comparison of forecasting results between BP network and multivariate statistics regression method |
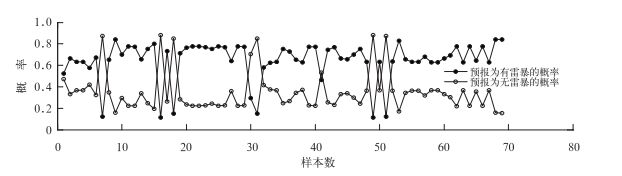
为对比双隐层BP网络在解决分类问题上的优势,图 4给出了单隐层BP网络的输出,同样以雷暴样本为例。可以看出,单隐层BP网络的预报结果两级化差异不如双隐层明显,这将导致预报难度大的样本出错的可能性更大,从数据上也验证了这一点,单隐层BP网络空报次数过多,导致TS评分降低。由此可见,在解决分类问题上,双隐层BP网络相对于单隐层BP网络有着一定的优势。
|
图 4 单隐层BP网络实际输出值特征 Fig. 4 Statistical characters of actual output from single hidden layer BP network |
(1) 在预报结果判定方面,网络采用单输出时,结果往往需要设定阈值来判定,而阈值的设置与雷暴的时空分布有关,数据预报结果可靠性不高。本文网络的输出采用二级分化,通过两级结果比较,可以直接判定雷暴发生与否,不需要设定阈值,可信度高。
(2) 在以往的研究中,雷暴预报多采取单隐层的BP网络。两个隐层的神经网络则可以解决各种分类问题,结果表明,双隐层BP网络在解决分类问题上有一定的优势。
(3) 为了寻找泛化能力最高的网络,对网络的输入进行了归一化处理,加快了网络训练速度,提高了网络的精度。针对训练数据进行分类,一定程度上避免了过拟合问题。传递函数及隐节点数的选取均尝试多种不同的组合,根据网络训练MSE最终确定最优组合。最后构建了针对本文研究内容的泛化能力较高的网络。
(4) 利用多元线性回归法和神经网络法进行雷暴预报的对比分析,采用相同的训练样本和独立检验样本,结果表明,与多元线性回归法相比,神经网络法在当地的雷暴预报中获得了更高的TS评分。
(5) 通过多组网络的预报结果,分析了雷暴预报结果的规律,表明了探空因子的变化与雷暴的发生有着密切的联系。
程炳岩, 郭渠, 张一, 等, 2011. 三峡库区高温气候特征及其预测试验[J]. 气象, 37(12): 1544-1552. DOI:10.7519/j.issn.1000-0526.2011.12.010 |
丛爽, 2003. MATLAB工具箱的神经网络理论与应用[M]. 合肥: 中国科学技术大学出版社.
|
高大启, 1998. 有教师的线性基本函数前向三层神精网络格构研究[J]. 计算机学报, 21(1): 80-86. |
官莉, 刘旸, 张雪慧, 2010. 人工神经网络算法在红外高光谱资料反演大气温度廓线中的应用[J]. 大气科学学报, 33(3): 341-346. |
金龙, 2004. 神经网络气象预报建模理论方法与应用[M]. 北京: 气象出版社.
|
李东风, 郑忠国, 2008. 最优线性回归的计算方法[J]. 数理统计与管理, 27(1): 87-95. |
刘宸钊, 卓伟, 裴军林, 2010. 基于对流参数的雷暴预报方法研究[J]. 高原山地气象研究, 30(2): 22-25. |
刘旸, 官莉, 2011. 人工神经网络法反演晴空大气湿度廓线的研究[J]. 气象, 37(3): 318-324. DOI:10.7519/j.issn.1000-0526.2011.03.009 |
农孟松, 黄海洪, 孙崇智, 等, 2011. 基于主分量神经网络的降水集成预报方法研究[J]. 气象, 37(3): 352-355. |
袁曾任, 1999. 人工神经网络及其应用[M]. 北京: 清华大学出版社.
|
张雪慧, 官莉, 王振会, 等, 2009. 利用人工神经网络方法反演大气温度廓线[J]. 气象, 35(11): 137-142. DOI:10.7519/j.issn.1000-0526.2009.11.018 |
赵旭寰, 王振会, 肖稳安, 等, 2009. 神经网络在雷暴预报中的应用初步研究[J]. 热带气象学报, 25(3): 357-360. |
郑栋, 张义军, 吕伟涛, 等, 2005. 大气不稳定度参数与闪电活动的预报[J]. 高原气象, 24(2): 196-203. |
Agostino M, 2005. Sounding-derived indices for neural network based short-term thunderstorm and rainfall forecasts[J]. Atmospheric Research, 83(3): 349-365. |
 2013, Vol. 39
2013, Vol. 39 