引言

由于受到地理位置及观测仪器等因素的影响，降水量的空间变率较大，因此获取精度较高的降水量格点化资料存在一定难度。在众多的插值算法中，克立格方法被认为是具有一定优势的方法。克立格方法是地统计学中重要的统计技术，主要原理是利用变异函数来表示区域化变量的内部关系。此方法在气象中的相关研究主要有：Geard等(1999)在海平面气压场的EOF空间上使用克立格方法对降水量进行了估计，表明估值精度有了提高；Barref(1988)根据日降水量，使用克立格方法对降水化学成分的分布和趋势变化进行了估计；Prudomne等(1998;1999) 使用克立格方法在地形复杂的山区对极端日降水量进行插值分析；Courault等(1999)对于不同的大气环流型使用地统计学方法做温度插值。魏凤英等(2002a;2002b)使用变异函数揭示了降水场空间变异结构并讨论了地统计学在气象中的应用；高歌等(2007)在1 km×1 km格点场上对日降水量开展插值分析，得到普通克立格方法效果好于反距离权重方法；使用普通克立格方法，进行中国热量资源精细化估算(王怀清等, 2011)。

根据研究目的和条件的不同，各种各样的克立格方法相继产生(Haas, 1990a)，如当区域化变量满足二阶平稳(或内蕴)假设时，可用普通克立格法；在非平稳条件下采用泛克立格法；当区域化变量服从对数正态分布时，可用对数正态克立格法；对有多个变量的协同区域化现象可用协同克立格法；对有特异值的数据可用指示克立格法等。当然，应用最为广泛的是普通克立格方法。Hass(1990b)利用观测站点资料对美国全国范围的待估点进行酸沉降估值时，较早地使用了滑动窗口的普通克立格方法(MWK)，结果表明，MWK对研究对象的空间分布估计更有效，而且提高了估值精度。Hass(1996)还进一步扩展了滑动窗口应用对象，在对数正态克立格方法、回归克立格方法和协克立格方法中也应用到了滑动窗口方法。Walter等(2001)在普通克立格方法中采用了滑动窗口方式估值；Lloyd等(2002)把滑动窗口方式用于泛克立格方法；Pardo-Iguzquiza等(2005)在泛克立格方法中使用滑动窗口方式对0~22°N和22°~44°E的区域1999年7月的250个测站的月降水量进行了分析。采用滑动窗口方式进行空间数据分析主要可用于气象、酸雨、土壤及高程；研究以上领域的数据样本都有覆盖范围广和数据量大的特点，是滑动窗口主要应用范畴。

一般认为，虽然降水在较大范围和不同方向上变化起伏大，但是在有限的局部区域中，降水量可以被近似地认为满足平稳和内蕴假设；在此前提下，对局部地区进行点的克立格方法估计会得到更为精确的降水量，因此，滑动窗口的普通克立格方法更适合降水量的格点化。本文在分析滑动窗口的普通克立格方法在降水量估值适用性分析基础上，针对存在的问题设计3种不同插值试验方案，比较了全局搜索与方位邻近方法的误差，讨论了最大影响半径及屏蔽效应对插值效果的作用。

1 MWK方法及其在降水量估值的适用性 1.1 普通克立格方法

设区域化变量R(X)满足二阶平稳及本征假设，其数学期望存在且等于常数，其协方差函数存在且平稳：

$E\left[ {R\left( x \right)} \right] = m$

(1)

${\text{Cov}}\left[ {R\left( x \right),R\left( {x + h} \right)} \right] = E\left[ {R\left( x \right)R\left( {x + h} \right)} \right] - {m^2} = C\left( h \right)$

(2)

变异函数γ(h)的估计量γ^*(h)是：

${\gamma ^*}\left( \mathit{\boldsymbol{h}} \right) = \frac{1}{{2N\left( \mathit{\boldsymbol{h}} \right)}}\sum\limits_{i = 1}^{N\left( h \right)} {{{\left[ {R\left( {{x_i}} \right) - R\left( {{x_i} + \mathit{\boldsymbol{h}}} \right)} \right]}^2}} $

(3)

式中，N(h)是被向量h相分隔的试验数据对的数目。

变异函数一般选择为球状模型：

$\gamma \left( \mathit{\boldsymbol{h}} \right) = \left\{ {\begin{array}{*{20}{l}} 0&{\mathit{\boldsymbol{h}} = 0} \\ {{C_0} + C\left( {\frac{{3\mathit{\boldsymbol{h}}}}{{2a}} - \frac{{1{\mathit{\boldsymbol{h}}^3}}}{{2{a^3}}}} \right)}&{0 ＜ \mathit{\boldsymbol{h}} \leqslant a} \\ {{C_0} + C}&{\mathit{\boldsymbol{h}} > a} \end{array}} \right.{\rm{ }}$

(4)

其中，C₀为块金常数，C为基台值，C₀+C为总基台值，a为变程。

1.2 滑动窗口的普通克立格方法

Journel等(1978)定义和讨论了准平稳过程，指出在相对大区域的非平稳过程，在子区域中表现出更小的变化趋势和更多的各向同性特点，因此，在子区域中可以近似地认为是准平稳的，这为滑动窗口的普通克立格方法(MWK)的广泛应用提供了理论基础。将大范围区域划分成许多子区域，并在子区域中对待估点使用普通克立格方法估值，这种方法就是MWK。以待估点为圆心，以最大影响半径所画的圆形覆盖区域称之为窗口，而窗口是随着位置不同的待估点而移动的。

与普通克立格方法不同的是，在实施MWK时，需要对每一观测值分别赋予一定的权系数，最后进行加权平均来估计待估点的数值。在无偏条件下，得到普通克立格方程组(侯景儒等, 1994)，在内蕴假设下，可用γ(h)表示如下：

$\left\{ {\begin{array}{*{20}{l}} \begin{gathered} \sum\limits_{\beta = 1}^n {{\lambda _\beta }\bar \gamma \left( {{\upsilon _\alpha },{\upsilon _\beta }} \right) + \mu = \bar \gamma \left( {{\upsilon _\alpha },V} \right)} \hfill \\ \sum\limits_{\beta = 1}^n {{\lambda _\beta } = 1} \hfill \\ \end{gathered} &{\left( {\alpha = 1.2. \cdots .n} \right)} \end{array}} \right.$

(5)

1.3 MWK在降水量估值中的适用性

降水量具有以下区域化变量的属性：(1) 空间局限性，站点降水量是空间点上在某个时间段内观测的降水累计量；(2) 连续性，这种连续性可以通过相邻样品之间的变异函数来描述，变异函数是能够对降水进行MWK插值的基础，通过变异函数可以得到较高精度的格点值；(3) 异向性，降水量在各个方向有不同的分布特点; (4) 相关性，降水量在一定范围内、一定程度上表现出空间相关性，对于普遍存在的过程性降水，这种相关性特点是显著的，即使是局地强对流天气，在一定观测密度下或在邻近的格点中，也可以有较好的相关性，当然，超出一定范围后相关性会逐渐减弱或消失。最后，站点的降水量数据具有范围大和随时间变化两大特点，符合MWK应用范围。

当使用MWK进行降水量插值时，为了取得更快运算效率和得到更为精确的估值，在适用方面应该考虑如下几点问题：

(1) 计算资源耗用大是各类克立格方法在气象领域应用中需要克服的难点，也是使用MWK进行降水估值中遇到的问题；这是由于各类克立格方法都要进行待估点和样本点之间、样本点之间的变异函数计算，还要进行克立格矩阵变换的计算，都会占用大量计算资源。虽然MWK已经把大区域细分成更小的子区域，客观上减少了参与插值的样本点，减少了计算耗时，但是，对于气象类资料分析还是不够。

(2) MWK对参与插值的样本并没要求它们具备空间拓扑结构，即在插值过程中只是对窗口内的数据点进行全局搜索，也就是说，窗口内的所有数据点都将参与插值，而没有考虑变量的特性和样本点分布特点。但是，降水量是具有空间相关和各向异性，同时，观测站点也是散乱分布的，若直接使用全局搜索对降水量插值，降低了计算效率，也可能会影响到插值精度。

(3) 理论变异函数的参数的计算至今没有好的方法，通常有两种拟合方法：一般是人工拟合法，就是首先给出实验变异函数，根据地质条件和人工经验，选择相应的变异函数模型，最终确定相关参数；另一种方法是自动拟合，使用加权多项式回归、线性规划、目标规划等多种数学手段拟合，但这些方法效果不太理想。上述两种方法在地质采矿的有限数据点的估值计算中可行的，但是对于气象中有上万个格点需要被估计时，其计算量和复杂度很难克服。

(4) 气象观测站点相距较远，一般是以每个行政县(区)为单位有一个降水人工观测站，测点相距数十千米到几百千米不等，同时站点分布也不规则，由此，气象站点疏密分布和高精度的地质勘探有较大的不同，当在应用MWK时要充分考虑此特点。

2 不同方案的MWK降水量插值误差的比较 2.1 试验方案

针对滑动窗口的普通克立格方法在降水量格点化应用中存在的问题，设计了3种试验方案。

2.1.1 试验方案1

使用方位邻近法筛选已知点。将全国2200个测站的降水量插值到0.28125°×0.28125°网格上，共有两万多个格点需要估值。虽然MWK缩小了采样范围，但是在观测较密集的中东部地区，传统的全局搜索法下的MWK仍然无法在当前的计算条件下正常运行。本文提出方位邻近法进行数据点选择，具体技术路线如下：将待估点为中心的360°圆内平均划分成32个方位，每个方位对应夹角是11.25°，在不同方位上选择距离圆心(待估点)最近的观测点作为采样点，若该圆的半径(即最大影响半径)足够大时，就有32个采样点，若圆的半径越小，采样点就越少。在挑选数据点时有4个方面的因素需要被考虑：

(1) 数据点的多寡直接影响到估值准确度和计算量；MWK运算复杂度是0[n³](徐建华, 2002)，过多的数据点，将增加克立格方程的维数，提高计算复杂度；若数据量偏少，较少的信息量也难以准确估值；试验表明，20多个数据点能达到较好的效果，因此平均划分成32个方位是比较理想的选择。

(2) 待估点周围的观测站散乱分布，各地域间站点疏密度相差较大，方位邻近法尽量使采样点均匀地分布在待估点周围，降低了站点散乱分布对格点估值过程的影响。

(3) 降水在大范围区域表现出明显的各向异性，而在小区域中，降水的各向异性有所减弱，这也是MWK得以应用的原因之一。

(4) 近邻性，选择距离格点最近的站点作为有效数据，在距离较近的情况下，降水量具有较好的相关性；距离过远降水量的相关性降低，会使变异函数模型的可靠性降低。全局法和方位邻近法相比较，全局法是以待估格点为中心，最大影响半径为圆的范围内的观测点都参与插值，由于站点数目决定了克立格方程维数，随着维数的增加，对计算环境要求就很高。本试验中，两种挑选站点方法的最大影响半径设置均为2°，ε(ε=C₀/C，ε为无量纲量)为0.1。

2.1.2 试验方案2

最大影响半径试验。最大影响半径是指在搜索样本点时的最远距离，在MWK中就相当于每个“窗口”的大小；如格点A(x₁, y₁)和格点B(x₂, y₂)，x和y分别是经度和纬度，假设经向和纬向每隔1°的物理距离相等，那么，两点间距离AB可以近似用多少度的弧长来表示：

$AB = \sqrt {{{\left( {{x_1} - {x_2}} \right)}^2} + {{\left( {{y_1} - {y_2}} \right)}^2}} $

由于要对每个格点分别建立方程求解待估值，格点所对应的变程和基台值的变异函数是可迁型的。变程a反映了待估点和已知点之间的关系，即区域化变量的影响范围。对于可迁型变异函数，以待估点z(x)中心，a为半径的影响范围内的已知点z(x+h)而言，距离z(x)愈近，则对z(x)影响愈大，反之愈小，当z(x+h)在影响区之外时，那么就没有影响了，因此a的大小关系到插值站点的选取。本文中，在不同方位上搜索观测点时能达到的最大距离，即最大影响半径，最大影响半径和每个格点的变程不是同一个概念；在方位邻近法下，以距离待估点最远采样点的距离为变程，因此每个格点的变程不仅和最大影响半径有关，还和观测站点的空间分布有密切联系；最大影响半径大致能反映出变程的变化范围，尤其是在站点观测稀疏的地区。观测点位置是以地理坐标系中的经纬度为单位表示，为了便于比较分析，可以用点之间经纬度的间隔表示距离远近；若最大影响半径过小[例如1°的经(纬)线弧长]，采样点则很少，在站点稀疏的西部地区就往往无样本点可以采集，若最大影响半径过大[例如大于10°的经(纬)线弧长]，用较远的观测样本参与插值，可能会产生较大的误差。所以，在方位邻近法下，最大影响半径从2°~10°的经(纬)线弧长，对全国范围的格点插值误差进行分析。最后，对格点周围32个方位都全部有数据点的情况下进行插值误差比较(对于边界点仍是部分方位有数据点)。在不同的最大影响半径对比中，ε取值固定为0.1。

2.1.3 试验方案3

块金效应(屏蔽效应)。地统计学上用变量ε表示块金(屏蔽)效应，ε=C₀/C，ε越小，屏蔽效应越强，反之，屏蔽效应越弱、块金效应强。ε取值由0.1~1.0共10个数值进行比较，试验中，使用方位邻近法采样，最大影响半径设为5°。所谓块金(屏蔽)效应就是数据点在方位和距离之间的相互影响。块金效应与观测尺度有密切关系，当测站间距大于降水结构范围时，就表现为块金效应；由式(4)，表示h很小时，两点间观测值的相关性。若已知点间呈现纯块金效应时，则取消了已知点之间的屏蔽效应，即在一个平稳带内进行估值，估计值就是已知数据点的平均数。

2.2 资料及误差检验方法

使用2009年1月1日至12月31日的全国2200个观测站(基本站和加密站)08时24小时实况降水量资料。插值格点格距为0.28125°×0.28125°。根据国家数值预报中心在预报产品评估中区划方法，把全国划分为8个区(图 1)：一区：东北，二区：新疆，三区：西北，四区：华北，五区：西藏，六区：西南，七区：长江中下游，八区：华南。

对于全国8个区域的降水量的MWK格点化效果采用交叉检验的方法进行检验，即用10次不重复随机地抽取观测值不参与插值，也就是说，每次有10%的站不参与插值，只使用90%的站进行格点插值。获得格点值后，通过双线性方法再插回到没有参与插值的站点上，然后算出其实际观测值和估算值之间的误差，以此评估插值方案的优劣。采用均方根误差、平均绝对误差和平均误差作为评估插值效果的标准。

2.3 不同方案的误差比较

试验方案1中8个区域的均方根误差、平均绝对误差和平均误差检验结果如表 1所示。从表 1可以看出，在站点比较密集的地区，例如长江中下游和华南地区，方位邻近法插值精度有一定的提高。若从计算耗时分析，在长江中下游地区的格点估值过程中，方位邻近法中参与格点插值计算的站点数大致在20左右，而全局法则达到50~60，按照MWK计算复杂度0(n³)分析，单个格点的全局搜索计算量是方位邻近的21倍，当数万个格点需估值时，对应有巨大的计算耗时。因此方位邻近法不但提高了插值准确率，而且大幅降低了计算耗时；更重要的是减少了克立格方程维数，降低了对计算机硬件的苛刻要求，当要对较多的格点进行估值时，方位邻近法才能满足普通机器环境下的日常业务需求，因而具有更为广泛的应用和推广价值。

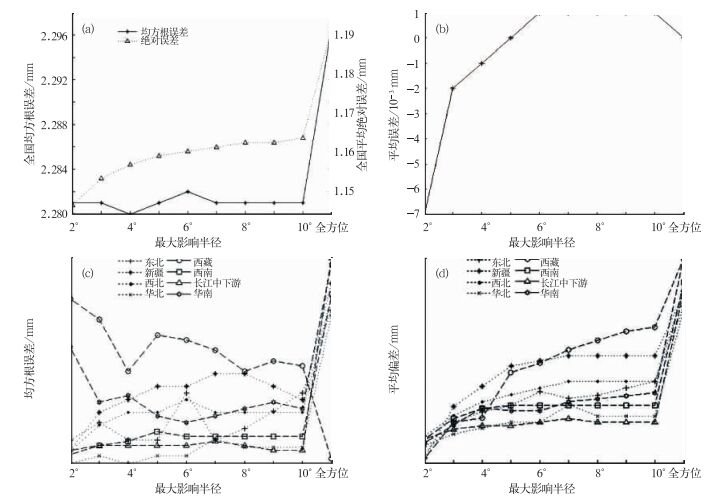
图 2表示最大影响半径取2°~10°的经(纬)线弧长和全方位(最大影响半径足够大，在方位邻近法中，32个方位的空间上都有站点参与对格点的插值，本文称之为全方位，即32个站点参与插值)时，均方根误差和平均绝对误差变化曲线(图 2a)，Y轴的左轴表示均方根误差，右轴为平均绝对误差。在2°~10°的经(纬)线弧长之间，全国范围内的均方根误差在2.28~2.282 mm之间；而在4°和6°的经(纬)线弧长则分别对应相对小(0.28 mm)和相对大(0.282 mm)值的两个点；10°经(纬)线弧长以内的其他点相应的均方根值相近。图 2a的平均绝对误差变化曲线中，在2°的经(纬)线弧长时平均绝对误差达到最小为1.147 mm，到3°时平均绝对误差增加较明显达到1.153 mm，在3°~10°的经(纬)线弧长之间，平均绝对误差缓慢上升。图 2b是平均误差变化曲线，从图可以看到，平均误差和绝对误差在变化趋势上有较大差异，特别是在最大影响半径取值较小时，两者呈现出相反的变化：最大影响半径为2°的经(纬)线弧长时，平均误差高达-0.007 mm，2°~5°的经(纬)线弧长之间则有较大幅度的减小，5°的经(纬)线弧长时的平均误差为0，5°的经(纬)线弧长之后，平均误差略增加并保持平缓的变化。当最大影响半径足够大时，均方根误差和平均绝对误差均达到最大，而平均误差接近0 mm，这说明当最大影响半径逐渐增大时，即参与插值的站点向32数值逐渐靠近时，插值误差会逐步放大，同时插值误差在偏大和偏小这两个正负区间摆动的幅度也会更剧烈。

为了比较方便，文中把8个区域的检验指标变化曲线放在同一张图中，由于每个区域的降水量相差很大，因此误差值会落在不同的量级，若用统一的Y轴刻度，曲线可能以近似直线形式显示，而无法比较分析；所以本文有关分区域比较图的纵坐标没刻度，图形表达的是变化图。图 2c是8个区域的均方根误差变化曲线，西南和长江中下游同全国平均走势相近，其均方根误差数值分别为3.08和3.19 mm；华南地区在2°~10°的经(纬)线弧长的变化范围内，2°的经(纬)线弧长时均方根误差偏大，其他影响半径对应的均方根误差变化特点和全国相近，其平均值达到5.02 mm；东北、新疆两区和西藏呈相反的变化特点，均方根误差值在1~2 mm之间；西北地区在半径比较小时，曲线走势难以确定，当半径大于7°的经(纬)线弧长之后，均方根增大；华北地区则在6°的经(纬)线弧长之后，变化趋势明确，均方根误差直线增大。均方根误差是误差离散度的指标，从分区检验比较中得出更有意义的结论，不同区域的变化揭示了空间散乱的站点和插值误差有密切关系，在实践中应具体问题具体分析，这一点不仅是MWK对应的问题，也是其他各种插值方法都要面对的难点；当用全国平均值进行检验分析时，往往会掩盖区域的不同特性。

8个分区的平均绝对误差和全国平均绝对误差变化特点基本一致(图 2d)，只是在不同分区中曲线的曲率变化略有不同。在降水量比较大的区域如：长江中下游、西南和华南3个地区在3°~10°的经(纬)线弧长之间变化不同或基本相近；这3个地区观测站点较密集，区域内各站点年季降水量差异小，当最大影响半径变化不大时，对各个格点进行插值的站点数变化不大，因而平均绝对误差相差也近似；但是，当最大影响半径明显增大时，平均绝对误差也显著增加，图 2d所示在全方位时，各个区域的平均绝对误差都有较大的增加。

由于8个区域的插值平均误差绘出的图形变化较复杂，将8个区的平均误差放在同一张表中(表 2)将有利于分析，从表 2中可以看出，8个区域的平均误差有较大的不同，东北、新疆和西藏在最大影响半径为2°的经(纬)线弧长是平均误差最大，分别是-0.009、-0.006和-0.053 mm；西藏西北的平均误差表现出相反的变化，例如，西藏地区平均误差从-0.053 mm逐渐减小到0 mm；从平均误差正负值来看，新疆、西藏和华南的平均误差为负，其他地区为正值；在部分区域平均误差的数值大小和降水量强弱关系不显著，总体来看，西藏和长江中下游平均误差的数值偏大，华北和西南偏小。可见平均误差大小和站点分布、降水分布特点及降水量有关，这些变量之间及其和平均误差的关系较复杂，但是当站点较疏散时，平均误差会明显增大。

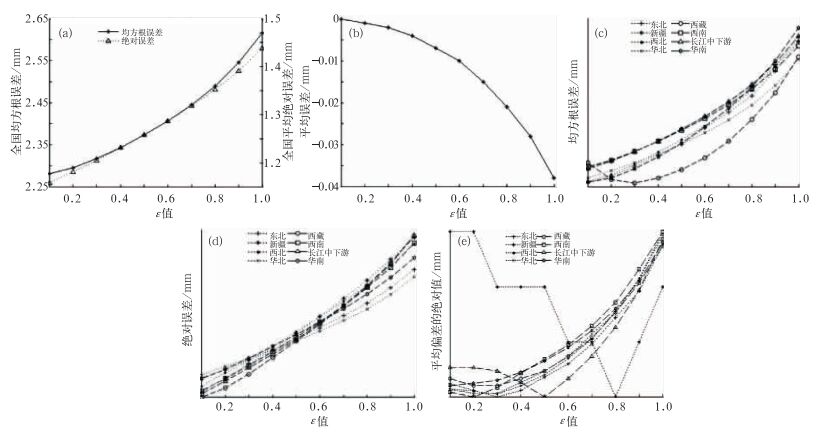
试验云案3的结果如图 3所示。从图 3a和3b可以看出，全国均方根误差、平均绝对误差和平均误差绝对值随着ε取值的增大呈现单调递增。当ε为0.1时，均方根、平均绝对误差和平均误差分别达到2.281、1.158和0 mm。图 3c和3d分别表示了8个区域的均方根和平均绝对误差变化曲线，分区域的变化趋势和全国平均值的单调递增格局保持一致。虽然大多数区域变化趋势相似，但是也有个别区域有些差异：在西藏地区的均方根在ε取0.1~0.3时，有较弱的减小；新疆有较大不同，当ε为0.1~0.2时，新疆平均误差达到-0.003 mm，随后逐步趋于0 mm，当ε为0.8时，平均误差也开始增大。长江中下游地区在0.5时达到最小值；平均误差(图 3e)最小值在大多数区域出现在ε为0.2或0.3，但是与ε为0.1时比较，误差变化幅度较弱。总体来看，均方根误差、平均绝对误差和平均误差都随着ε值增大而增大，只是在个别地区，由于站点分布和降水结构有较大不同，导致误差变化趋势略有差异。

3 小结与讨论

针对传统MWK直接应用到降水量插值中遇到的问题，本文提出了不同的技术处理方案，使该方法在降水中使用更趋合理。通过不同方案的误差比较得到以下结论：

(1) 使用适量的已知点对于插值的精度很重要。当已知点过多时，会使插值准确率下降，因为过多的信息量会掩盖有用的信息，这与降水量空间相关性有密切关系；因此对于每个待估格点，在已有的资料的情况下，寻找适量的已知点是插值要面对的重要问题。

(2) 以待估点为中心，在平均划分的32个方位上选择距离最近观测点作为样本点，显著降低了计算耗时、减少了存储开销，同时可获得较高的插值准确度。在观测站点密集地区，方位邻近法具有明显的优势。

(3) 最大影响半径和变程呈正相关关系(以离待估点最远的样本点的距离作为变程)，在相同的最大影响半径下，使用方位邻近法时，每个格点的变程是有差别的。在散乱数据点中，变程是数据点的空间相关性的反映；变程大，则相关尺度也大，说明降水量的变化比较缓和；变程小，相关性小，降水量变化较剧烈。以上特性在站点稀疏的西藏和降水局地变化较强的华南地区有较典型的反映。

(4) 变程的变化对各个区域插值精度的影响呈现复杂变化，在降水量大、站点较密集的中东部地区，当最大影响半径选择在4°~5°的经(纬)线弧长时，均方根误差、平均绝对误差和平均误差达到较低的数值，从气象学角度能得到较好的解释，一般天气尺度的降水系统24小时的移距在1000 km左右，其对应的降水覆盖半径也就在4°~5°的经(纬)线弧长之间。

(5) 使用衡量变量的空间相关程度的ε值进行试验的结果表明，ε等于0.1时，我国大部分地区的插值准确率较高，当ε逐渐增大时，准确率也随之降低，说明降水的块金效应较弱，屏蔽效应强，观测站的降水量有显著的空间相关性。