引言

热带低频振荡会影响中国的降水。在低频振荡强度高的年，对流活跃中心位于热带印度洋(热带西太平洋)时，中国南方降水偏多。而强度低的年，各位相的对流、降水以及其他要素的异常均不明显(冯俊阳等，2012)。Chen等(1991)指出30°N以南的季节内振荡西传明显，常与副热带高压西移有关，甚至可以影响四川旱涝。吴国雄等(1999)认为从南半球向北传播的季节内振荡和从西太平洋向西传播的频率2~3周的低频(TTO)在东亚季风区锁相时，亚洲季风阶段性爆发。热带大气季节内振荡(the Madden-Julian oscillation，MJO)是热带低频振荡的一种，由Madden等(1971)在研究太平洋风场和气压场时最先发现，周期一般在30~60 d之间，普遍存在于热带大气中，向东传播。而其他的热带低频振荡或季节内振荡，也会向西、向北传播。MJO对热带地区的天气气候有直接影响，也可明显的调制副热带、中高纬度的天气气候(Jones，2000；Bond et al, 2003)。陈丽臻等(1994)分析了长江流域两个典型旱涝年的MJO特征，发现涝年MJO明显，而旱年MJO不明显。

目前应用MJO资料制作月降水预测研究不多，业务应用更少。引进新的、有明确物理意义的因子，是提高月降水预测准确率的一条重要途经。MJO振荡周期一般在30~60 d，因而上月MJO有可能影响下月降水。MJO相关资料现在可从网站下载，为业务应用提供了可能，研究应用MJO资料制作月降水预测，显然有助于月降水预测准确率的提高。

1 资料与方法

实时多变量MJO指数取自CAWCR(The Centre for Australian Weather and Climate Research)，可从网站http://cawcr.gov.au/staff/mwheeler/maproom/RMM/下载，通过以下步骤得到：(1) 逐日15°S~15°N经向平均的向外长波辐射(Outgoing Longwave Radiation，OLR)，850、200 hPa纬向风资料去除年循环和年际变率，使得与MJO相关的季节内时间尺度上有最大的变率。(2) 处理后的OLR，850和200 hPa纬向风联合EOF。(3) EOF的前两个时间系数被称为RMM1和RMM2，分别解释总方差的12.8%和12.2%，非常接近，因而RMM1和RMM2几乎同等重要。每日以RMM1和RMM2的值为横坐标和纵坐标确定点，然后按日期先后逐点连接，就可得到MJO的轨迹图。定义$\sqrt {RMM{1^2} + RMM{2^2}} $为MJO的振幅，振幅小于1的为弱MJO，即RMM1、O、RMM2平面上以原点O为圆心，1为半径的圆内点为弱MJO。圆内点移动相对随机，无明显规律。而圆外的点多数绕原点逆时针转动，表明了MJO系统性的向东传播。(4) 与EOF的第一、二空间函数对应，RMM1、O、RMM2平面分为8个空间位相，大致表征MJO对流所在的地理位置：8和1为西半球、非洲，2和3为印度洋，4和5为海洋大陆，6和7为西太平洋。

由于OLR缺测，1978年3月17日至12月31日无资料。

长江流域降水取自国家气候中心中国大陆160个代表站中25°~34°N、100°E以东范围内59个测站资料。

奇异值分解(singular value decomposition，SVD)是近年发展起来的分析场与场关系的方法，被认为具有广泛的应用前景(Bretherton et al, 1992；张礼平等，2004)。RMM1和RMM2一起表征MJO所在的地理位置，振幅表征MJO强度，RMM1、RMM2、振幅3个变量一起较全面地描述了MJO。显然，MJO不同的地理位置、强度，其影响是不一样的。用上月平均RMM1、RMM2和振幅构造为右场(3个变量)，下月长江流域降水场为左场(59个变量)，SVD分析上月MJO与下月长江流域降水场的关联，试验上月MJO预测下月长江流域降水的可能性。

2 MJO资料处理

逐日的RMM1、RMM2、振幅数据包含了高频的脉动，不便于直接作为气候预测的预报因子。考虑到每月25日以前的RMM1、RMM2、振幅月底可以得到，在月底制作的下月预测具有实际意义，1—25日数据平均接近月平均，将每月1—25日数据相加，然后除以25，代替该月平均的RMM1和RMM2、振幅。经处理后的数据既滤去了高频的脉动，也使得尺度与月相当。

在20世纪70年代中期前后，海洋和大气发生了显著年代际气候突变，且1979年1月1日后才有连续MJO资料，为了避开年代际气候突变，同时也为计算方便，统计样本均始于1979年1月。

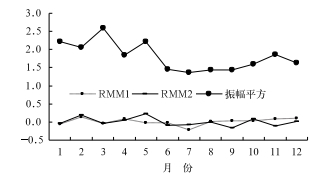
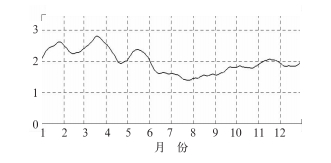
计算每月RMM1、RMM2、振幅×振幅1979—2012年平均值，振幅×振幅6—10月均不超出1.6，最小值出现在7月(1.36)，其他月均大于1.6，最大值出现在3月(2.59)，其次为1和5月，表明北半球的冬半年MJO较北半球的夏半年活跃, 最活跃在3月, 最不活跃在7月(图 1和图 2)，与北半球冬季亚澳季风区赤道附近Hadley环流上升气流明显强于北半球夏季对应。其季节循环与网站http://cawcr.gov.au/staff/mwheeler/maproom/RMM/给出的31天滑动平均表征的季节循环基本一致，说明由1—25日数据相加平均代替月平均是可行的(参见图 1和图 2)。

3 预测方案

上月RMM1和RMM2、振幅应对下月有直接影响，因而有可能影响下月长江流域降水，设计用上月RMM1、RMM2、振幅预测下月降水。SVD得到的两场时间系数的协方差较大，因而可能存在某种关系。考虑到线性函数是最简单的函数形式，且右场(上月RMM1和RMM2、振幅)仅有3个变量，前两模态的可预报性最大，构造时间系数估计公式为(张礼平等，2005)

$ {a_1} = {c_{01}} + {c_{11}}{b_1}\\ {a_2} = {c_{02}} + {c_{12}}{b_2} $

(1)

式中, a₁、b₁分别为左场(降水场)和右场(上月RMM1、RMM2和振幅)第一时间系数，a₂、b₂分别为第二时间系数，c₀₁、c₁₁、c₀₂和c₁₂为待定系数。借助最优化技术，在降水场距平与实况距平同号的总站数最大意义下确定合理的系数c₀₁、c₁₁、c₀₂和c₁₂，由此建立估计公式(1)。将RMM1、RMM2、振幅3个变量SVD第一、二时间系数b₁、b₂代入式(1)，估计降水场第一、二时间系数a₁、a₂，求得a₁、a₂后, a₁、a₂与对应空间函数线性组合即可得到降水预报场。方案考虑的是RMM1、RMM2、振幅综合对降水场的主要耦合关系，重点考虑可预报的大尺度信号，滤去不可预报的小扰动，尽可能使估计的降水场距平与实况距平同号率最大，从而提高技巧水平。

我们选用遗传算法(genetic algorithms, GA)。GA明显优于传统的局部搜索算法(如梯度法、单纯形算法等)，GA取得高质量解的代价，在于大幅度増加的计算量和存储量。有幸的是，对于计算机技术高速发展的今天，这已不成为问题。

按照上述方案，我们对长江流域月降水场分别进行拟合和独立预测试验。用1979—2010年逐年12月RMM1、RMM2、振幅拟合预测次年1980—2011年逐年1月降水，用2011年12月RMM1、RMM2、振幅独立预测2012年1月降水。用1979—2011年逐年1月RMM1、RMM2、振幅拟合预测1979—2011年逐年2月降水，用2012年1月RMM1、RMM2、振幅独立预测2012年2月降水，余此类推，独立预测2012年1—12月降水，其中建模分析样本容量为32、33不等。

用蒙特卡罗法检验SVD结果的统计显著性。设置不重复的随机数种子初值，利用随机数发生器生成正态分布随机序列，构造与实例相同行和列的2个矩阵为左、右场，进行100次模拟SVD计算，结果为每次计算的第一模态可解释总协方差的部分(SCF₁)都小于18%，按大小排序，第五位也一定小于18%。本文的12实例中第一模态的SCF₁都在38%及以上，因而均超过0.05显著性水平检验(表 1)。

第一模态相关系数12实例中仅9、12月超过0.05显著性水平检验，表明多数上月MJO与下月长江流域降水场两场的线性相关并不密切，因而不便分析相关结构。

尽管多数的月第一模态的线性相关并不密切，但1—12月实例距平符号预测拟合率都在0.57或以上，其中有4个月在0.70以上，1、7和11月都超过0.80，表明存在较明显非线性关系，且其中部分非线性关系被本方案归纳。2012年1—12月共12个独立预测中有9个预测距平符号与实况距平同号率大于0.50(随机预报同号率)，占总数75%，表明具有一定的预测能力(表 1)。1月预测距平符号拟合率和独立预测同号率均较高，可能与振幅大(MJO对流活跃)有关。

4 结语

用RMM1和RMM2、振幅1—25日平均代替月平均，上月月平均RMM1和RMM2、振幅构造为右场，下月长江流域降水场为左场，SVD分析上月MJO与下月长江流域降水场的关联，借助最优化技术，在降水场距平与实况距平同号的站数最大意义下确定合理的系数，建立估计公式，由右场SVD时间系数估计左场时间系数，考虑RMM1、RMM2、振幅综合对降水场的主要耦合关系，重点考虑可预报的大尺度信号，滤去不可预报的小扰动，尽可能使估计的降水场距平与实况距平同号率最大，从而提高技巧水平。

尽管多数的月SVD第一模态相关并不显著，但1—12月距平符号预测拟合率都在0.57或以上，其中有4个月在0.70以上。2012年1—12月共12个独立预测中有9个月预测距平符号与实况距平同号率大于随机预报同号率，占总数75%。证实虽然本方案估计公式形式上是线性的，但是非线性的遗传算法，使得本方案具有归纳非线性关系的能力，也表明上月MJO有潜力预测下月长江流域降水，且上月MJO数据可在网上方便下载，为时实业务应用提供了可能。今后，随着分析样本的增多，预测能力还有望进一步提高。