2. 中国科学院大学,北京 100049;
3. 中国气象局数值预报中心,北京 100081;
4. 美国犹他州立大学,犹他 84321;
5. 中国科学院寒区旱区环境与工程研究所寒旱区陆面过程和气候变化重点实验室,兰州 730000;
6. 南京信息工程大学大气环境中心,南京 210044
2. University of Chinese Academy of Sciences, Beijing 100049;
3. CMA Numerical Prediction Centre, Beijing 100081;
4. Utah State University, Utah, 84321 USA;
5. Key Laboratory for Land Surface Process and Climate Change in Cold and Arid Regions, Cold and Arid Regions Environmental and Engineering Research Institute, Chinese Academy of Sciences, Lanzhou 730000;
6. Yale -NUIST Center on Atmospheric Environment, Nanjing University of Information Science and Technology, Nanjing 210044
湖泊作为下垫面的一种,是陆面过程研究的重要组成部分。据统计,湖泊面积大约占全球陆面总面积的3% (Downing et al, 2006)。湖泊及其周边湿地是人类生活、栖息的主要场所,湖盆流域兴衰决定了社会兴亡和民族兴盛。从20世纪50年代开始,湖泊对天气和气候的影响越来越为人们所重视(Laird et al, 2010; Rouse et al, 2008; Samuelsson et al, 2001; Kristovich et al, 1998; Lofgren, 1997)。位于加拿大和美国东北角交界处的五大湖(Great Lakes),由于其巨大的水域面积,对当地的天气和气候有着不可比拟的影响。因此早在20世纪初气象学家们就开始研究五大湖对天气系统的影响。近10年来,科学家们利用可能获得的观测资料(探空资料、雷达、卫星云图、地面观测等)以及数值模式,采用统计分析和数值模拟相结合的方法,从天气学和气候学的角度研究了五大湖等大型湖泊的湖效应降水,开展了包括大尺度天气背景、物理过程、预报指标等方面的综合分析与研究,并取得了大量的科研成果(Goyette et al, 2000; Wiggin, 1950)。太湖是中国五大淡水湖之一,水域面积排第三。太湖湖面平均海拔3.33 m,最深达4.8 m,面积2338 km2。太湖位于江苏省南部,邻接浙江省,是我国经济最发达、产业最密集的地区之一。近年来,随着社会经济的发展,太湖流域的水污染问题日益严重,流域对水资源质量要求越来越高,洪涝灾害对社会经济发展造成的影响越来越大。另一方面,在全球气候变暖的大背景下,区域气候变暖将使水文循环加快,造成陆地降水分布不均匀,旱涝等自然灾害的发生频率和危害程度均有可能增加。自20世纪90年代以来,已有学者对气候变化对太湖最高水位(尹义星等,2009)、蓝藻(商兆堂等,2010;王成林等,2010;武胜利等,2009)的影响,以及夏季风与洪旱灾害间的相互关系(王宝荣,1992;尹义星等,2010)进行了研究。结果表明太湖流域气温升高、降水减少、日照时数增多,造成太湖最高水位降低和蓝藻暴发频繁。也有许多学者开展了太湖流域土地利用对太湖流域水文过程影响的研究(高俊峰,2002;万荣荣等,2009;李恒鹏等,2007)。太湖流域河网密集、水文过程复杂,湖泊对区域天气与气候影响的研究亟待进一步深入与加强。
随着科学技术特别是计算机计算能力的快速提高,人们越来越倾向于通过数值模式来模拟和预报湖泊过程和湖效应的降水(Lavoie, 1972;Ballentine, 1982; Hjelmfelt et al, 1983)。虽然用数值模式开展对湖泊效应降水的模拟和预报已经展开,但这些模式中都没有包含湖面模块。湖气耦合模式对于动态地预报湖泊过程和湖气相互作用是一个很重要的工具。但当前的数值模式对湖泊的处理都过于简单。Goyette等(2000)把一个耦合了简单湖模式的区域气候模式应用到美国五大湖,但是这个简单的湖模式不能显式地处理湖泊内的能量传输和它们的季节变化。目前广泛使用的天气研究和预报模型(如WRF3.0) 对大面积湖区的湖温处理是采用类似海表温度的处理办法通过插值得到,而对次网格尺度的湖区则忽略不计(Skamarock et al, 2005)。WRF模式自从3.1版本以后,考虑了冬季湖泊冰和水在模式单位网格里的比例分配,在一定程度上改进了模式对冬季湖泊陆面过程的描述。但是,考虑到湖泊和气候系统的相互影响,耦合湖泊模式到天气和气候模式中变得尤为重要。耦合的湖泊模式从天气和气候模式中得到强迫场后,能通过自身物理过程计算反馈给天气和气候模式湖泊表面边界条件,如湖水温度、反照率、感热和潜热通量。
在本研究中,我们耦合了一个一维湖泊模式到中尺度数值大气模式WRF3.2中,并利用2010年在太湖梅梁湾获得的观测资料对该耦合模式在太湖的模拟能力进行了初步评估。
1 模式和数据介绍本研究所用的湖模式最初为一个一维的10层湖模式,这个10层湖模式是综合陆面模式(CLM)3.5版(Oleson et al, 2004)的一个子块,最初是由Hostetler(1993)和Hostetler等(1994)的研究发展而来的。在CLM的湖面方案的基础上,Subin等(2012)在湖泊的底部又添加了10层的土壤层,在湖泊顶部湖冰上添加了最多5层的雪层,并对湖冰进行参数化。
该湖模式主要由三部分组成。第一部分由大气的强迫场计算出湖水的表面温度,同时各种通量如动量通量。感热通量和水汽通量等也一并计算出来;第二部分是模式的核心部分,计算各个垂直层次(20~25层,包括最多5层雪层,以及10层湖水和湖底以下10层土壤)的温度,用Crank-Nicholson方法把一维的热扩散方程写成差分形式,离散化的方程组可以整理成三对角矩阵的形式,很方便地求解出各层的温度;第三部分是湖泊的水文过程,详细考虑了湖泊中水的三相变化以及雪的挤压等,但是没有考虑雪的渗透。
湖泊内部的能量传送考虑分子扩散和湍流扩散来计算。在该模式中,分子扩散系数为常数(1.433×10-7 m2·s-1),近地面的风场和湖水的密度梯度用来参数化计算湍流扩散系数(Henderson-Sellers et al, 1983; Henderson-Sellers, 1985)。当湖表温度低于太湖湖水的冻结温度时,模式中不再考虑湍流扩散的作用。任一层的湖水允许任意比例的冻结,湖水的冻结将释放潜热从而加热湖水或湖泊上层的空气。对流混合可以在湖水的任何一层发生,即使那一层的湖水已经冻结。模式中有雪层出现的时候没有太阳光进入湖泊,反之,湖面上没有雪层出现时,则太阳光可以穿透湖水到达湖泊的底部,到达底部的太阳光则被湖泊底部的第一层土壤层吸收。湖泊的深度可以根据实际情况有不同的深度,对任意深度的湖泊假设其物理过程都是适用的。更为具体的关于该湖模式的介绍见古红萍等(2013)。
本研究中,我们将该湖泊模块作为独立的模块耦合到WRF3.2版本中。湖泊模块的调用是紧接着陆面过程调用完之后进行,湖面模块从大气模式读入所需的强迫场(太阳辐射、风、气压、湿度、降水模式最底层温度等)后,通过湖模块自身复杂物理过程的计算后,把计算结果(如湖表温度,2 m空气温度和比湿,感、潜热通量等)反馈给大气模式,更新大气模式中的这些变量。湖面模块每步调用一次。该耦合模式可以视研究区域的具体情况,选择开启或关闭湖面模块。在默认的设置中,所有湖泊深度被定为50 m, 分为10层。在本研究中,仍然采用10层的垂直分层,根据太湖的实际情况把水深设为1.9 m。设置湖泊模式表层深度为0.1 m,以此来更好地反映近地层变量的日变化规律(Kourzeneva, 2010),湖泊模式中各层的厚度从第二层到湖泊最底层逐渐增加,各层中心深度分别为0.050、0.195、0.385、0.575、0.765、0.955、1.145、1.335、1.525和1.715 m。模式10层水温采用太湖梅梁湾观测的水温插值到模式中进行初始化。由于本研究时段太湖没有雪出现,所以模式不调用积雪的处理模块。
本文用来检验该耦合模式的模拟能力。所用的观测资料为南京信息工程大学大气环境中心提供的2010年8月11—28日的太湖梅梁湾的观测资料。该观测资料的时间间隔为半小时一次,包括常规气象观测(空气温度、湖表面温度、气压、相对湿度和风向风速)、以及非常规观测包括通量的观测(感、潜热通量)、辐射观测(向上和向下的短波辐射和长波辐射)以及湖水不同深度(0.2、0.5、1.5和1.9 m)水温的观测。
2 模式配置和试验设计模拟试验的初始和边界条件均来源于NCEP提供的每6 h一次1°×1°的再分析资料。模拟起止时间为2010年8月11日00时至28日24时,共18 d。模式模拟区域为27/9/3 km三重嵌套(图 1), 最内区覆盖整个太湖,分辨率达到3 km。模拟试验中所使用的主要物理方案包括:Thompson云微物理参数化方案,Grell-Devenyi集成对流参数化方案,最内层关闭对流参数化方案,NOAH陆面过程方案,Bougeault and Lacarrère边界层方案(PBL), Dudhia短波辐射和RRTM长波辐射方案。关闭嵌套反馈作用,模式积分时间步长为60 s,模式最内层每小时输出一次模拟结果。
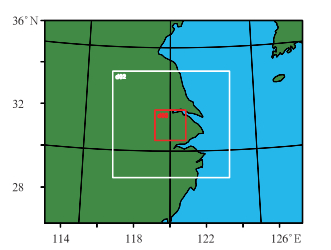
|
图 1 模式三重嵌套示意图 Fig. 1 Schematic diagram of three nested model grid |
本文设计了三组针对太湖的模拟对照试验:(1) 没有加入湖模块的WRF模式(WRF);(2) 没有对参数进行优化的原始耦合模式(WRF_Lake_Old); (3) 对3个参数进行优化后的耦合模式(WRF_Lake_New)。在这三组试验中,将试验WRF和WRF_Lake_Old的模拟结果进行比较,旨在说明耦合湖模式到大气模式中对模式模拟能力的改进;试验WRF_Lake_Old和WRF_Lake_New的对照则用于研究参数优化对耦合模式模拟能力的提高。
3 结果和分析 3.1 耦合模式模拟的湖表温度首先选取太湖上的观测站点梅梁湾(31.4°N、120.2°E)观测的2010年8月11—28日每半小时一次的湖表温度(LST)的观测资料来评估该耦合的湖气模式模拟湖温的能力。这里需要说明的是,下文所使用的模拟结果均来自第三重嵌套区域的模拟结果(图 2),图 2中蓝色代表植被类型为水体(太湖)。把格点的模拟结果插值到站点梅梁湾所在的经纬度,并将模拟的逐小时的湖表温度与观测的湖温(实线)做对比(图 3),图 3中点为WRF的模拟结果,虚线为WRF_Lake_Old的模拟结果。从该图中可以发现,耦合的湖气模式(WRF_Lake_Old)模拟的湖表温度比没有包含湖面模块(WRF)的模拟结果有了明显的改进。没有包含湖面模块的WRF模式中,没有专门的物理模块来处理下垫面为水体的格点,对于水体的处理是采用类似海表温度的办法通过插值得到的。因此该WRF模拟的湖表温度实际是从每6 h一次的模式驱动场直接获得的,并不是模式计算的结果。耦合了湖面模块的湖气耦合模式每一步调用湖面模块,湖面模块从大气模式获得必要的强迫场(如太阳辐射、风、气压、湿度和降水等)后,通过湖模块自身复杂物理过程的计算后,把计算结果(如湖表温度、2 m空气温度,感、潜热通量等)反馈给大气模式,更新大气模式中的这些物理量。因此湖气模式模拟的湖表温度是湖泊模块与大气模式耦合作用的结果。
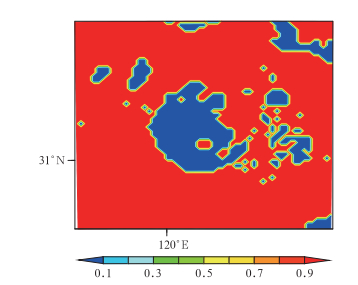
|
图 2 第三重嵌套区域的植被类型示意图 [蓝色代表水体(太湖)] Fig. 2 Schematic diagram of vegetation type for domain 3 [Blue color represents water (Taihu Lake)] |
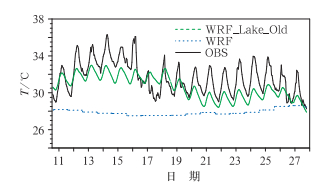
|
图 3 2010年8月11—28日站点梅梁湾每小时的湖表温度(LST)变化序列图(单位: ℃) (观测:黑线,WRF模拟:蓝线,WRF_Lake_Old模拟:绿线) Fig. 3 Time series of hourly LST (unit: ℃) at Meiliangwan Station from observations (black line), WRF simulations (blue line) and WRF_Lake_Old simulations (green line) from 11 to 28 August 2010 |
从图 3中可以清楚地看到,该耦合模式能够反映出湖表温度应有的日变化,并且模拟的湖温与WRF的模拟结果相比更靠近观测,因此该耦合模式是成功的。但是我们也发现,该耦合模式模拟的湖温与观测还存在较大的偏差,模拟的湖表温度比观测偏低3℃左右;模拟的湖温日变化明显偏小2~3℃,模拟的湖温日变化的幅度为1℃左右,而实际观测的太湖晴天湖表温度的变化为3~4℃左右。这些都说明在把该湖气耦合模式应用于研究太湖的湖泊过程及太湖对区域天气与气候的影响之前,需要对该耦合模式在太湖进行进一步的测试,找出模拟误差产生的原因及解决方法,使该耦合模式能够模拟出跟观测比较接近的湖表温度。从而为湖气相互作用的研究提供一个比较理想的工具。
3.2 模拟误差的分析该耦合模式模拟的湖表温度与观测相比存在较大偏差的来源有两个可能性,一是来自于大气模式模拟的大气强迫场的误差,二是来自于湖面模块本身计算产生的误差。我们首先从第二个可能性入手,也就是考察这个湖模式本身是否适用于太湖这类型的湖泊研究。
Subin等(2012)、Martynov等(2010)和Stepanenko等(2010)对该湖模式实施的离线测试表明该湖模式对非浑浊水体的浅湖的研究是适用的。我们知道湖泊的光学性质除了和湖泊的深浅有关以外,还和湖泊中的污染程度、悬浮物体的种类和大小以及湖中的生态环境息息相关。古红萍等(2013)通过调研发现由于太湖的富营养化程度高,水质污染严重,而且8月正是蓝藻暴发期,这些都造成了太湖湖水光学性质的明显改变。而古红萍等(2013)通过在太湖梅梁湾同一时段采用观测资料驱动该湖泊模式的离线测试结果发现,该湖模式最初在太湖的离线测试结果并不理想,模拟的湖表面温度与观测对比有较大的系统性偏差,并且温度的日变化的幅度与观测相比也偏小。古红萍等进一步分析了该湖模式对太湖的模拟效果不理想的原因,具体分析了太湖的生态环境和污染情况,设计了18个测试参数的敏感性的试验,从敏感性试验的结果分析得到,适合于太湖的依赖于湖泊的类型决定的三个参数的取值分别应为:消光系数(η0)应放大3倍,湖泊表层吸收的太阳辐射系数(β)应取0.8,粗糙长度z0采用公式计算得到。古红萍等用新得到的适合于太湖的3个参数重新进行了模拟,并与最初的模拟结果和观测资料对比,发现采用新的参数后的模拟结果比最初的模拟结果有了很大的改进。因此本文根据古红萍等在太湖的离线测试结果,对湖气耦合模式中依赖于湖泊决定的3个参数进行优化,参数优化后的模拟结果见图 4。从该图我们发现WRF_Lake_New(虚线)比WRF_Lake_Old(点线)的模拟结果有了明显改进,模拟的湖表温度日变化和平均值都跟观测更为靠近,参数优化后模拟的湖表温度误差平均在±1℃左右,与古红萍等(2013)离线测试的结果一致,即参数优化后的模拟结果有了明显提高。
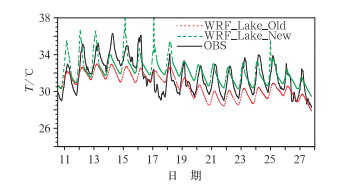
|
图 4 2010年8月11—28日站点梅梁湾每小时的湖表温度(LST)变化序列图(单位: ℃) (观测:黑线,WRF_Lake_Old模拟:红线, WRF_Lake_New模拟:绿线) Fig. 4 Time series of hourly LST (unit: ℃) at Meiliangwan Station from observations (black line), WRF_Lake_Old simulations (red line) and WRF_Lake_New simulations (green line) from 11 to 28 August 2010 |
我们发现,虽然参数优化后的模式模拟结果比之前有了较大的改进,但是跟古红萍等(2013)在太湖使用相同湖泊模式的用观测资料驱动的离线模拟结果相比,WRF_Lake_New未能模拟17—18日的湖表温度下降,离线模拟结果则可以把这一天气转折给模拟出来。因此猜测这两天的模拟误差大的原因可能是大气模式的强迫场误差所致。古红萍等(2013)对输入湖模式的主要的大气参量(太阳辐射、2 m的空气温度以及风场)的±10%的误差引起的模式模拟的太湖湖表面温度的误差进行分析表明,该一维湖泊模式的模拟结果对太湖上空的风场最不敏感,对辐射和气温的敏感度相当。WRF模拟的向下长波和短波辐射通量不受湖面过程的影响,可以代表大气模式本身的误差,因此我们把WRF模拟的向下长波和短波辐射通量与观测作比较。图 5是2010年8月11—28日站点梅梁湾每小时的向下短波辐射(图 5a)和长波波辐射(图 5b)时间变化序列图。从图 5b中可以看出WRF模拟(点线)的长波辐射跟观测(实线)比较一致,误差范围在±20 W·m-2之间;而图 5a WRF模拟的短波辐射在11—19日与观测比存在较大的偏差,模式预报的向下短波辐射比观测平均偏多了150 W·m-2左右,特别是17日,模式模拟的最大短波辐射与观测相比偏多了将近400 W·m-2。我们调查了模拟时段2010年8月11—28日这18 d的天气情况,发现17和18日为阴天,而大气模式没有把这一过程模拟出来,导致模拟的短波辐射偏差较大。由此我们得出结论WRF_Lake_New模拟的17—18日湖表温度的偏差很大一部分应该是来自于模式提供的大气强迫场误差所致。
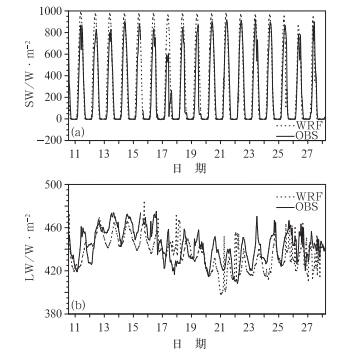
|
图 5 2010年8月11—28日站点梅梁湾每小时的向下短波辐射(a)和长波波辐射(b)时间变化序列图(单位: W·m-2) (观测:实线,WRF模拟:点线) Fig. 5 Time series of hourly (a) downward short wave radiation and (b) downward long wave radiation (unit: W·m-2) at Meiliangwan Station from observations (solid line), WRF simulations (dotted line) from 11 to 28 August 2010 |
为了更直观看出参数优化后耦合湖面模块对太湖模拟能力的提高,我们把太湖观测的湖表温度、2 m空气温度以及感、潜热通量分别与WRF和WRF_Lake_New的模拟结果作了对比。图 6是2010年8月11—28日站点梅梁湾每小时的2 m空气温度和湖表温度(LST)的时间变化序列图。总的来说WRF_Lake_New模拟的湖表温度跟2 m空气温度与WRF相比都与观测更为接近。WRF_Lake_New模拟的湖表温度的平均误差在±1℃以内,而WRF模拟的湖表温度与观测相比则存在较大的偏差,平均偏低4℃左右;WRF_Lake_New模拟的2 m空气温度除17和18日外,其余跟观测的吻合得很好,平均偏差在±0.5℃左右。比WRF的模拟结果有了很大的改进。图 7是模式模拟的感、潜热通量与观测的对比图,从图 7中可以看出WRF模拟的感热通量存在较大的偏差,由于WRF模拟的湖表温度与观测偏低较多(最大偏差达-6℃),模拟的湖面温度比空气温度低,模拟的感热通量的方向与观测相反,为负值。WRF_Lake_New模拟的结果则比WRF有了明显的改进,能合理地模拟出太湖上部边界层感、潜热通量的交换,能模拟出感潜热通量明显的日变化,模拟与观测比较接近。
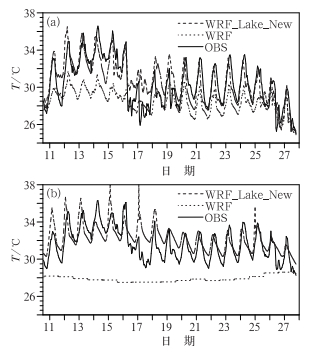
|
图 6 2010年8月11—28日站点梅梁湾每小时的(a)2 m空气温度(b)湖表温度(LST)的时间变化序列图(单位: ℃) (观测:实线, WRF模拟:点线, WRF_Lake_New模拟:虚线) Fig. 6 Time series of hourly (a) 2 m air temperature and (b) LST (unit: ℃) at Meiliangwan Station from observations (solid line), WRF simulations (dotted line) and WRF_Lake_New simulations (dashed line) from 11 to 28 August 2010 |
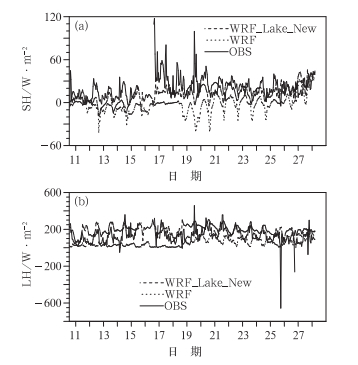
|
图 7 2010年8月11—28日站点梅梁湾每小时的(a)感热通量和(b)潜热通量的时间变化序列图(单位:W·m-2) (观测:实线,WRF模拟:点线,WRF_Lake_New模拟:虚线) Fig. 7 Time series of hourly (a) sensible heat flux and (b) latent heat flux (unit: W·m-2) at Meiliangwan Station from observations (solid line), WRF simulations (dotted line) and WRF_Lake_New simulations (dashed line) from 11 to 28 August 2010 |
以上的分析结果表明,耦合了湖面模块,并且参数优化后的湖气耦合模式(WRF_Lake_New)比没有参数优化的耦合模式(WRF_Lake_Old)和没有包含湖面方案的WRF模式(WRF)对太湖的模拟能力有很大提高。模拟的湖表温度能够真实反映湖表温度的日变化,模拟的湖表温度误差范围平均在±1℃左右,模拟的空气温度平均误差范围在±0.5℃以内,模拟的感、潜热通量也与观测更为接近。这些研究结果表明该耦合的湖气模式能够用于今后中国湖区及湖气相互作用的研究,但是在把耦合模式用到具体的湖泊中时,需针对湖泊的具体情况进行对依赖于湖泊决定的参数优化后才能得到更理想的模拟结果。
4 结论和讨论本文把一维热扩散湖模式成功耦合到中尺度天气研究和预报模式WRF3.2中,建立了WRF_Lake湖气耦合模式,该耦合模式能动态地模拟出湖泊与大气之间的能量交换。并用太湖梅梁湾获得的2010年8月11—28日的观测资料对该耦合模式模拟湖温的能力进行了初步评估。测试设计了3组试验方案进行对照试验,分别为(1) 没有加入湖模块的WRF模式(WRF)试验;(2) 没有对参数进行优化的原始耦合模式试验(WRF_Lake_Old); (3) 对3个参数进行优化后的耦合模式试验(WRF_Lake_New)。试验结果表明,耦合模式(WRF_Lake_Old)的模拟结果比没有耦合湖面模块(WRF)模拟的湖表温度有了明显的提高,耦合模式能合理地模拟出湖表温度的日变化,而且模拟的湖表温度也与观测更接近,但是发现耦合模式模拟的湖面温度与观测相比还存在系统性的偏低,而且模拟的湖表温度的日变化也偏小。我们从湖模式本身和大气强迫场两方面入手,分析误差产生的可能原因。通过调研发现该湖模式用到太湖这类浑浊水体时,需对湖泊的3个参数进行优化;分析大气强迫场发现,大气模式模拟的向下太阳短波辐射过多,也是模拟误差产生的另一个原因。文章最后采用离线测试得到的3个参数优化的方法,对耦合模式进行同样的参数优化后发现模式(WRF_Lake_New)的模拟结果有了显著的改善。模拟的湖表温度能够真实反映湖温的日变化,湖表温度的模拟误差范围平均减少到了±1℃左右,模拟的近地面空气温度与观测非常接近,平均误差范围在±0.5℃以内,模拟的感、潜热通量也与观测更为接近。这些研究结果表明该耦合的湖气模式为今后中国湖区及湖气相互作用的研究提供了一个有力的工具,但是在把该耦合模式用到具体的湖泊中时,需针对湖泊的具体情况对依赖于湖泊类型决定的参数进行优化才能得到更为理想的模拟结果。
另外,需要指出的是,由于湖泊的观测资料目前还比较少,本文的测试结果是基于太湖梅梁湾2010年8月11—28日的观测资料得到的,具有一定的局限性。对于太湖其他地点、其他时段则还需要更多的测试;并且本研究3个参数的优化方法也是针对太湖的,对于其他相同类型的湖泊研究仍需进一步的验证。
致谢:本文研究所用的太湖的水温、辐射以及通量等各种观测资料要特别感谢以下项目和基金:江苏省基础研究计划(自然科学基金)面上研究项目(BK2011830),教育部长江学者和创新团队发展计划项目(PCSIRT)和江苏高校优势学科建设工程项目(PAPD);国家自然科学基金项目(41275024)。
高俊峰, 2002. 太湖流域土地利用变化及洪涝灾害响应[J]. 自然资源学报, 17(2): 150-156. DOI:10.11849/zrzyxb.2002.02.004 |
古红萍, 沈学顺, 金继明, 等, 2013. 一维热扩散湖模式在太湖的应用研究[J]. 气象学报, 71(4): 719-730. DOI:10.11676/qxxb2013.051 |
李恒鹏, 杨桂山, 金洋, 2007. 太湖流域土地利用变化的水文响应模拟[J]. 湖泊科学, 19(5): 527-543. |
商兆堂, 任健, 秦铭荣, 等, 2010. 气候变化与太湖蓝藻暴发的关系[J]. 生态学杂志, 29(1): 55-61. |
万荣荣, 杨桂山, 2009. 流域土地利用/覆被对洪峰的影响研究——以太湖上游西苕溪流域为例[J]. 自然资源学报, 24(2): 318-327. DOI:10.11849/zrzyxb.2009.02.017 |
王宝荣, 1992. 淮河、太湖流域1991年洪涝灾害学术交流会在蚌埠召开[J]. 气象, 18(7): 65. DOI:10.7519/j.issn.1000-0526.1992.07.014 |
王成林, 潘维玉, 韩月琪, 等, 2010. 全球气候变化对太湖蓝藻水华发展演变的影响[J]. 中国环境科学, 30(6): 822-828. |
武胜利, 刘诚, 孙军, 等, 2009. 卫星遥感太湖蓝藻水华分布及其气象影响要素分析[J]. 气象, 35(1): 18-23. DOI:10.7519/j.issn.1000-0526.2009.01.003 |
尹义星, 许有鹏, 陈莹, 2009. 1950—2003年太湖流域洪旱灾害变化与东亚夏季风的关系[J]. 冰川冻土, 32(2): 381-388. |
尹义星, 许有鹏, 陈莹, 2010. 太湖最高水位及其与气候变化、人类活动的关系[J]. 长江流域资源与环境, 18(7): 609-614. |
Ballentine R J, 1982. Numerical simulation of land-breeze-induced snowbands along the western shore of Lake Michigan[J]. Mon Wea Rev, 110(11): 1544-1553. DOI:10.1175/1520-0493(1982)110<1544:NSOLBI>2.0.CO;2 |
Downing J A, Prairie Y T, et al, 2006. The global abundance and size distribution of lakes, ponds, and impoundments[J]. Limnol Oceanogr, 51(5): 2388-2397. DOI:10.4319/lo.2006.51.5.2388 |
Goyette S, McFarlane N A, Flato G M, 2000. Application of the Canadian regional climate model to the Laurentian great lakes region: Implementation of a lake model[J]. Atmosphere-Ocean, 38(3): 481-503. DOI:10.1080/07055900.2000.9649657 |
Henderson-Sellers B, McCormick MJ, Scavia D, 1983. A comparison of the formulation for eddy diffusion in two one-dimensional stratification models[J]. Appl Math Modelling, 7: 212-215. DOI:10.1016/0307-904X(83)90010-0 |
Henderson-Sellers B, 1985. New formulation of eddy diffusion thermocline models[J]. Appl Math Modelling, 9: 441-446. DOI:10.1016/0307-904X(85)90110-6 |
Hjelmfelt M R, Braham R R, 1983. Numerical simulation of the airflow over Lake Michigan for a major lake-effect snow event[J]. Mon Wea Rev, 111: 205-219. DOI:10.1175/1520-0493(1983)111<0205:NSOTAO>2.0.CO;2 |
Kourzeneva E, 2010. External data for lake parameterization in numerical weather prediction and climate modeling[J]. Boreal Envir Res, 15: 165-177. |
Hostetler S W, 1993. Interactive coupling of a lake thermal model with a regional climate model[J]. J Geophys Res, 98: 5045-5057. DOI:10.1029/92JD02843 |
Hostetler S W, Giorgi F, Bates C T, et al, 1994. Lake-atmosphere feedbacks associated with Paleolakes Bonneville Lahontan[J]. Sci, 263(5147): 665-668. DOI:10.1126/science.263.5147.665 |
Kristovich D A R, Braham R R, 1998. Mean profiles of moisture fluxes in snow-filled boundary layers[J]. Bound-Layer Meteor, 87: 195-215. DOI:10.1023/A:1000836401204 |
Laird N F, Desrochers J, et al, 2010. Climatology of lake-effect precipitation events over Lake Champlain[J]. J Appl Meteor Climatol, 48(2): 232-250. |
Lavoie R L, 1972. A mesoscale model of lake effect snowstorms[J]. J Atmos Sci, 29: 1025-1040. DOI:10.1175/1520-0469(1972)029<1025:AMNMOL>2.0.CO;2 |
Lofgren B M, 1997. Simulated effects of idealized Laurentian Great Lakes on regional and large-scale climate[J]. J Climate, 10(11): 2847-2858. DOI:10.1175/1520-0442(1997)010<2847:SEOILG>2.0.CO;2 |
Martynov A, Sushama L, Laprise R, 2010. Simulation of temperate freezing lakes by one-dimensional lake models: Performance assessment for interactive coupling with regional climate models[J]. Boreal Env Res, 15: 143-164. |
Oleson KW, Dai Y, Bonan G, et al.2004.Technical description of the community land model (CLM). NCAR/TN-461+STR, 174.
|
Rouse W R, Blanken P D, Bussieres N, et al, 2008. Investigation of the thermal and energy balance regimes of Great Slave and Great Bear Lakes[J]. J Hydrometeorol, 9: 1318-1333. DOI:10.1175/2008JHM977.1 |
Samuelsson P, Tjernstrim M, 2001. Mesoscale flow modification induced by land-lake surface temperature and roughness differences[J]. J Geophys Res, 106(D12): 12419-12435. DOI:10.1029/2001JD900057 |
Skamarock W C, Klemp J B, Dudhia J, et al.2005.A Description of the Advanced Research WRF Version 3. Mesoscale and Microscale Meteorology Division, National Center for Atmospheric Research, NCAR/TN-475+STR. http://www.mmm.ucar.edu/wrf/users/docs/arw_v3.pdf.
|
Stepanenko V M, Goyette S, Martynov A, et al, 2010. First steps of a lake model intercomparison project: lakeMIP[J]. Boreal Envir Res, 15: 191-202. |
Subin ZM, Riley WJ, Mironov D, 2012. An improved lake model for climate simulations: Model structure, evaluation, and sensitivity analyses in CESM1[J]. J Adv Model Earth Syst, 4: M02001. |
Wiggin B L, 1950. Great snows of the Great Lakes[J]. Weatherwise, 3(6): 123-126. DOI:10.1080/00431672.1950.9927065 |
 2014, Vol. 40
2014, Vol. 40 
