2. 中国气象科学研究院,北京 100081
2. Chinese Academy of Meteorological Sciences, Beijing 100081
利用催化剂进行人工增雨、防雹、消云、消雾等各类人工影响天气的作业和科学试验中(Scheaefer, 1946),催化剂入云后的扩散范围、质粒浓度的时空分布等都与催化作用和效果直接相关,因此,了解和掌握催化剂的扩散规律和时空分布,进行科学的作业设计非常重要。我国人工影响天气实际业务的需求很大,各地日常进行着大量的人工增雨作业,采用高炮、火箭和飞机等运载工具,播撒AgI催化剂直接进入符合条件的云区播撒催化。然而,催化后的有效范围如何确定,催化有效区域随时间如何变化,如何进行催化播撒才能保证一定区域、一定时段内的充分催化等作业设计,这些都是人影业务中亟待解决的重要问题。
这方面的研究国内外也开展过一些工作,比如,申亿铭等(1986)对催化剂的输送扩散做过大量研究,主要基于有限差分法对飞机播撒催化剂做了研究,并考虑了催化剂质点速度随高度的变化(申亿铭,1982a)。利用湍流的梯度输送理论(申亿铭,1994),提出了层状云及对流云中线源(申亿铭,1983a)和点源催化剂扩散的理论模式(申亿铭,1982b; 1983b);并研究了飞机播撒催化剂的叠加效应(申亿铭,1983b)及风速的垂直变化对催化剂扩散的影响。为催化剂在云中的扩散机制和浓度的时空分布的研究提供了理论基础。余兴等(1998)利用三维烟团数值模式模拟催化剂在云中的扩散,结合飞机人工增雨作业的一次个例(余兴等,2005a),对过冷层状云中播云产生的有效区域(余兴等,2002)、催化剂水平输送和扩散速率等进行了模拟研究(余兴等,2007)。对飞机人工增雨作业中的作业间距设计(余兴等,2005b)、作业催化剂用量、作业催化有效区域、人工增雨播撒方法等进行了理论研究和探讨(戴进等,2006)。
国外对催化剂的输送扩散主要采用示踪试验和数值模式相结合的方法。Hill(1980)用两架飞机对冬季地形云进行了试验和理论研究。播撒催化剂的形式分为两种:一种在山上的上风方沿北—南方向播撒,形成瞬时线源;另一种则围绕固定点做椭圆飞行,形成连续点源。Holroyd等(1988)采用一系列冬季飞机示踪试验确定了科罗拉多大方山地区从高空和地面播撒AgI烟羽湍流输送的特征,得到结论:飞机播撒的AgI横向扩散速度在多云情况下超过2 m·s-1,晴空时略低。Bruintjes等(1995)等用三维时变网格模式来计算北亚利桑那复杂地形下示踪物或播云物质的扩散,并将模式计算结果与观测做了对比。Li等(1997)将地面播云的高斯烟羽扩散模式同地形云模式结合起来,研究了不同的冰晶生成机制如何从本质上影响降水效率和强度。
然而,以往国内外的催化扩散研究工作,基本偏重于催化扩散的理论研究和个例探讨,计算模型和试验也较复杂,没能针对高炮、火箭和飞机等实际业务中不同方式的不同播撒情况进行针对性的研究,给出实际不同情况播撒后扩散影响的有效区域确定的计算系统,特别对高炮、火箭和飞机等实际的作业设计缺乏研究,更缺乏方便的软件系统提供业务应用。
本文基于扩散计算解析解,根据实际人影业务作业高炮、火箭和飞机不同播撒方式,研究计算催化剂以点源、线源、移动点源等形式在静止和平流不同云区情况下的扩散范围和浓度分布等,并同实际飞机播云成冰区的卫星实测结果作对比,检验计算的可信度。同时根据现有的人工影响天气理论研究(比如,播云一般人工冰晶的浓度应达到104 m-3才能对降水过程有显著作用等研究结果),根据计算所得的扩散范围和浓度分布,结合人工降水所需要达到的冰晶浓度,进一步探讨人工增雨充分催化最佳播撒作业方案的设计等,对实现充分播撒高炮作业的间距分布和炮弹发数,以及飞机飞行作业的充分播撒催化的路线和方案设计进行研究。为我国实际的人工影响天气高炮、火箭和飞机飞行作业设计和作业效果分析提供依据和指导。
1 不同播撒方式催化剂扩散计算方案 1.1 出发方程在自由大气中的物质输送扩散方程具有如下形式:
| $ \begin{array}{*{20}{l}} {\frac{{\partial q}}{{\partial t}} + u\frac{{\partial q}}{{\partial x}} + v\frac{{\partial q}}{{\partial y}} + w\frac{{\partial q}}{{\partial z}} = }\\ {{k_H}\frac{{{\partial ^2}q}}{{\partial {x^2}}} ++ {k_H}\frac{{{\partial ^2}q}}{{\partial {y^2}}} + {k_v}\frac{{{\partial ^2}q}}{{\partial {z^2}}}} \end{array} $ | (1) |
式中,q为扩散物质浓度;u、v、w分别代表x、y、z轴上的分风速;kH和kV分别为水平和垂直方向上的湍流系数(m2·s-1);t为时间。
由于研究范围较小,时间较短,大气观测资料有限,所以认为大气环境是水平均匀的,即u、v和k为常数,由实测催化层的风速确定,w=0。式中水平湍流交换系数kH,同垂直系数kV是不同的。由于催化剂的浓度远高于背景值,扩散过程的尺度变化较大,从几十米到几千米,采用数值计算时,确定格距是个难题。而且,自由大气的扩散观测较少,湍流特征值表达式的不确定性大,所以解析解是较好的近似。
根据苏联对云中湍流部分的研究工作,层状云云中的湍流系数kH和kV约为50~70 m2·s-1,而积云云内的湍流系数则较大,约为70~100 m2·s-1,积雨云云内的湍流系数更大,可达到150~200 m2·s-1。实际作业的层状云往往不是单纯的层状云,会包含一些对流泡等,积层混合云比较多,且水平方向上的湍流系数往往要比垂直方向上的湍流系数大。为了研究其对扩散结果的敏感性,在计算中,我们取kH=70 m2·s-1, kV=35 m2·s-1和kH=140 m2·s-1, kV=70 m2·s-1。
1.2 瞬时点源——高炮作业带有催化剂的高炮炮弹,发射到云中爆炸后,催化剂被迅速分散到一个较小的球形空间(dxdydz)范围内,在湍流作用之下不断向四周扩散,视为瞬时点源。
设在初始时刻t=t0时,x0、y0和z0处播撒初始总量Q[源强,催化剂(单位:g)或冰核(单位:个)]的催化剂,即催化剂浓度
由于播撒高度较高,可以不考虑地面的反射作用。瞬时点源(高炮作业)的数值解析解为:
| $ \begin{array}{*{20}{l}} {q\left({x, y, z, t} \right) = \frac{Q}{{8\sqrt {{\pi ^3}k_H^2{k_V}{{\left({t - {t_0}} \right)}^3}} }}{{\rm{e}}^{ - \frac{{{{\left[ {x - {x_0} - u\left({t - {t_0}} \right)} \right]}^2}}}{{4{k_H}\left({t - {t_0}} \right)}}}} \times }\\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{\rm{e}}^{ - \frac{{{{\left[ {y - {y_0} - v\left({t - {t_0}} \right)} \right]}^2}}}{{4{k_H}\left({t - {t_0}} \right)}}}}{{\rm{e}}^{ - \frac{{{{\left[ {z - {z_0} - w\left({t - {t_0}} \right)} \right]}^2}}}{{4{k_V}\left({t - {t_0}} \right)}}}}} \end{array} $ | (2) |
在多个点源情况下,格点的催化剂浓度应是各点源(xi, yi, zi)释放的源强Qi的作用总和,可用加法进行计算。即:
| $ \begin{array}{*{20}{l}} {q\left({x, y, z, t} \right) = \sum\limits_{i = 1}^N {\frac{{{Q_i}}}{{8\sqrt {{\pi ^3}k_H^2{k_V}{{\left({t - {t_0}} \right)}^3}} }} \times } }\\ {\;\;\;\;{{\rm{e}}^{\frac{{ - {{\left[ {x - {x_i} - u\left({t - {t_0}} \right)} \right]}^2}}}{{4{k_H}\left({t - {t_0}} \right)}}}}{{\rm{e}}^{\frac{{ - {{\left[ {y - {y_i} - v\left({t - {t_0}} \right)} \right]}^2}}}{{4{k_H}\left({t - {t_0}} \right)}}}}{{\rm{e}}^{\frac{{ - {{\left[ {z - {z_i} - w\left({t - {t_0}} \right)} \right]}^2}}}{{4{k_V}\left({t - {t_0}} \right)}}}}} \end{array} $ | (3) |
因此高炮的催化扩散研究,采用瞬时多点源方案的计算。
1.3 瞬时线源——火箭作业火箭或局部飞机播撒的催化剂构成一条或多条直线,如果不考虑播撒时间的差别,可视作瞬时线源。设播撒线同y轴一致且无穷长,则其解析解为
| $ q = \frac{Q}{{4\sqrt {{\pi ^2}{k_H}{k_V}{t^2}} }}{{\rm{e}}^{ - \frac{{{{\left[ {x - {x_0} - u\left({t - {t_0}} \right)} \right]}^2}}}{{4{k_H}\left({t - {t_0}} \right)}}}}{{\rm{e}}^{ - \frac{{{{\left({z - {z_0}} \right)}^2}}}{{4{k_V}\left({t - {t_0}} \right)}}}} $ | (4) |
式中,Q为单位长度上的催化剂量(单位:g·m-1或个·m-1),即源强,q为催化剂浓度(单位:g·m-3或个·m-3)。
在多个平行线源作用下,各点各时刻的催化剂浓度为
| $ \begin{array}{*{20}{l}} {q\left({x, y, z, t} \right) = \sum\limits_{i = 1}^N {\frac{{{Q_i}}}{{4\sqrt {{\pi ^2}{k_H}{k_V}{t^2}} }} \times } }\\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{\rm{e}}^{\frac{{ - {{\left[ {x - {x_i} - u\left({t - {t_0}} \right)} \right]}^2}}}{{4{k_H}\left({t - {t_0}} \right)}}}}{{\rm{e}}^{\frac{{ - {{\left[ {z - {z_i} - w\left({t - {t_0}} \right)} \right]}^2}}}{{4{k_V}\left({t - {t_0}} \right)}}}}} \end{array} $ | (5) |
式中,N为平行线源数,xi和zi为i个平行线源的所在位置,Qi为其源强。
因此火箭和部分飞机催化扩散研究,可采用瞬时多线源方案的计算。
1.4 移动点源——飞机作业飞机播撒的持续时间很长,同瞬时线源有较大差异,我们可以把移动点源离散化,看作是每隔Δt的tn时刻在对应的xn,yn,zn处播撒Qn=RΔt,R为播撒速率,单位为g·s-1或个·s-1。飞机播撒的浓度应是相加的结果。即
| $ \begin{array}{*{20}{l}} {{q_n}\left({x, y, z, t} \right) = \frac{{{Q_n}}}{{8\sqrt {{\pi ^3}k_H^2{k_V}{{\left({t - {t_n} + {t^*}} \right)}^3}} }} \times }\\ {\;\;\;\;\;\;{{\rm{e}}^{ - \frac{{{{\left[ {x - {x_n} - u\left({t - {t_n}} \right)} \right]}^2}}}{{4{k_H}\left({t - {t_n} + {t^*}} \right)}}}}{{\rm{e}}^{ - \frac{{{{\left[ {y - {y_n} - v\left({t - {t_n}} \right)} \right]}^2}}}{{4{k_H}\left({t - {t_n} + {t^*}} \right)}}}}{{\rm{e}}^{ - \frac{{{{\left[ {z - {z_n} - w\left({t - {t_n}} \right)} \right]}^2}}}{{4{k_V}\left({t - {t_n} + {t^*}} \right)}}}}}\\ {\ln {q_n} = \ln {Q_n} - \ln 8 - \frac{3}{2}\ln \pi - \ln {k_H} - \frac{1}{2}\ln {k_V} - }\\ {\;\;\frac{3}{2}\ln \left({t - {t_n} + {t_0}} \right) - \frac{{{{\left[ {x - {x_n} - u\left({t - {t_n}} \right)} \right]}^2}}}{{4{k_H}\left({t - {t_n} + {t_0}} \right)}} - }\\ {\frac{{{{\left[ {y - {y_n} - v\left({t - {t_n}} \right)} \right]}^2}}}{{4{k_H}\left({t - {t_n} + {t_0}} \right)}} - \frac{{{{\left[ {z - {z_n} - w\left({t - {t_n}} \right)} \right]}^2}}}{{4{k_V}\left({t - {t_n} + {t_0}} \right)}}} \end{array} $ | (6) |
式中,x、y、z和t为任一空间时间坐标,xn、yn、zn和tn为第n个飞机播撒点的四维精确坐标,由飞机GPS实测输入。飞机播撒点(xn, yn, zn, tn)取每秒一次的间隔,距离为Va×1 s,Va为飞机航速,单位为m·s-1。如果播撒1 h,则N=3600(n=1, 2, …, k, …, N)。如果飞机航速为100 m·s-1,则间距为100 m,总长为360 km。
考虑到每段飞机播撒实际不是点源,而有一定初始宽度和长度,所以在模式中用点源在t*时段扩展后的状态来模拟会更接近实际情况,模式中t*取10 s。
因此,飞机催化扩散的计算研究,采用移动点源方案的计算更接近实际。
2 高炮催化作业的扩散规律、有效范围及作业设计为计算不同播撒方式扩散规律和催化扩散有效范围,首先需明确有效浓度的概念和阈值。在人工冰核的扩散计算中,取大于一定浓度阈值的区域作为有效催化区。在层状云中往往观测到自然冰晶浓度大大低于104 m-3。有人提出在有过冷水的条件下的冰晶少于2×104 m-3为强可播区,反之为弱可播区。一般人工冰晶的浓度应达到104 m-3才能对降水过程有显著作用,数值模拟研究也支持这一点(史月琴,2008)。取104 m-3的人工冰核浓度作为显著有效区的阈值,而103 m-3作为有效区阈值。在以下的计算中,用实际催化剂在-10℃时的成冰数作为源强,利用数值解的结果讨论高炮作为瞬时点源的扩散问题。点源计算时,若考虑风速,扩散影响的范围和时间会受到风速情况的影响,无法获得单独高炮扩散情况,为获得确切的一枚及多枚高炮影响区域和时间,在以下计算中均认为是在静力均匀下的情况, 即u=v=w=0。
2.1 单发炮弹作业扩散规律单个炮弹在云中爆炸后,炮弹里的催化剂在云中的扩散可以看作是点源催化剂在云中扩散。取一枚炮弹含AgI为1 g,成核率为1011 g-1(中国气象局,2003),输入源强Q为1011个,扩散系数分别为kH=70 m2·s-1, kV=35 m2·s-1和kH=140 m2·s-1, kV=70 m2·s-1,用式(2) 在u=v=w=0情况下计算得到的单个点源过源点的x轴方向上的浓度剖面如图 1所示。取浓度(103 m-3)作为催化有效区阈值。

|
图 1 单发炮弹作业点源过x0、y0和z0扩散浓度剖面q(x)随时间演变 (图a为kH=70 m2·s-1, kV=35 m2·s-1,图b为kH=140 m2·s-1, kV=70 m2·s-1,其中纵坐标为扩散浓度的对数,红色虚线为103 m-3的阈值,绿色虚线为102 m-3的阈值) Fig. 1 Single shell point source diffusion concentration profile q(x) cross x0, y0, z0 evolution with time (The left is kH=70 m2·s-1, kV=35 m2·s-1, the right is kH=140 m2·s-1, kV=70 m2·s-1, of which vertical axis presents logarithm of diffusion concentration, the red dotted line is the threshold value of 103 m-3, and the green dotted line is the threshold value of 102 m-3) |
由于垂直湍流交换系数小于水平的,瞬时点源的催化剂浓度分布呈椭球状。中心浓度最大,向四周减小。各时刻沿水平中心轴的浓度分布剖面列于图 1。
由图 1可以看到,(1) 催化中心浓度随时间增加逐渐减小,减小速度先快后慢,范围扩大;湍流系数越大,过程越快。(2) 浓度达到103 m-3的催化有效范围随着时间先增大后减小,直至消失。如图中所示,当扩散系数为kH=70 m2·s-1, kV=35 m2·s-1时,达到103 m-3阈值的扩散宽度在4 min前只能达到0.5 km,相应面积约为
z轴方向上的扩散浓度剖面同图 1相似。由于kV较小,故垂直扩散较慢。在6 min前扩散宽度达到约0.3 km。在云中,扩散达到103 m-3的体积约为
由于高炮弹成核率较低,一发炮弹造成有效催化区域较小,面积最大为0.2 km2,体积只能达到约0.04 km3,能够达到有效催化的持续时间较短,只有不到5 min。如果成核率提高10倍,整个浓度都成正比的加大10倍。此时浓度分布图像基本不变,只是纵坐标lgq提高1。此时103 m-3的位置相当图 1中102 m-3,即绿色虚线,可见最大有效催化区直径可达0.75 km,维持超过20 min。由以上计算可以看出,单个的高炮作业催化区域过小,维持时间也太短,无法达到播云增雨的作用。故在实际作业中,一般采取多发炮弹同时作业的方案。
2.2 多发炮弹作业扩散规律和作业设计高炮作业时,怎样设计炮弹弹着点,间距应当为多少才能够达到有效催化是所需要解决的问题。以下用式(3)u=v=w=0情况下,计算多个炮弹同时在云中爆炸的浓度时空分布,分别计算了相距为1000 m的3发炮弹爆炸和相距300 m的5发炮弹爆炸的浓度时空分布(见图 2),源强Q为1011个,扩散系数为kH=70 m2·s-1, kV=35 m2·s-1。

|
图 2 间距1000 m的3发炮弹扩散浓度剖面(a)和间距300 m的5发炮弹扩散浓度剖面(b) (纵坐标同图 1) Fig. 2 Diffusion concentration profiles of 3 shells with 1000 m interval (a) and 5 shells with 300 m interval (b) (vertical axis same as Fig. 1) |
图 2中的图 2a相距为1000 m的3发炮弹爆炸后10 min时,催化剂浓度在3 km直径范围内只能维持在102 m-3左右。在图 2b中相距300 m的5发炮弹,可在1.5 km范围内维持103 m-3的浓度约3 min,10 min内,催化剂浓度能在约2 km范围内维持300 m-3以上。可以看到,采用较小的炮弹发射间距,如300 m,有利于催化剂较高浓度的维持。所以,在实际高炮作业中,提高炮弹的成核率并采用较小空间间隔,如300 m,密集发射,有利于起到更好的催化作用。
若设计高炮作业为4×4个炮弹分别以300 m间隔排列同时作业,则可得到区域内平面浓度分布如图 3所示。

|
图 3 4×4排列间隔300 m的16发高炮作业平面催化扩散浓度分布 (a)扩散2 min浓度平面分布图,(b)扩散4 min浓度平面分布图,(c)扩散10 min浓度平面分布图,(d)扩散30 min浓度平面分布图 Fig. 3 The cloud seeding diffusion concentration planar of 16 shells arranged as 4×4 which interval is 300 m at work (a) the concentration planar distribution after diffused 2 minutes, (b) the concentration planar distribution after diffused 4 minutes, (c) the concentration planar distribution after diffused 10 minutes, (d) the concentration planar distribution after diffused 30 minutes |
由图 3可以看到,2 min时,催化区域中是一个一个分别独立的圆形扩散带,整个催化区域内都可保持大于4×103 m-3的浓度,达到阈值浓度的催化范围可达到0.81 km2以上;4 min时,扩散区变成一个连续的、均匀的扩散带,但催化区域开始减小,浓度开始降低,达到3×103 m-3的催化范围为0.64 km2,整个扩散区域基本仍可以保持103 m-3阈值以上浓度;到10 min,扩散的浓度持续降低,但整个区域仍可以保持103 m-3阈值以上浓度;直到30 min,扩散区域中心最大浓度也只有不到103 m-3,整个区域内没有达到阈值浓度的可被有效催化的点。
由此可见,4×4排列的16枚炮弹可以保证在10 min内维持103 m-3,可以保证在30 min内维持102 m-3,若将成核率提高10倍,则一定区域内能被有效催化的时间可达30 min以上,所以,提高炮弹成核率和密集排列多个高炮同时作业,是高炮作业中能够取得较好作业效果的关键。
3 火箭飞机线源催化扩散规律、有效范围及作业设计实际中火箭和飞机播撒,同高炮点源播撒不同,视为一条或多条一定间距的直线,火箭作业可视为瞬时线源,飞机播撒也可近似看作瞬时线源。可以用式(4) 来计算催化剂浓度的扩散宽度。火箭和飞机的线源源强可用所携带焰剂成核总量除以燃烧距离来获得。
首先给出我国火箭和飞机业务作业常用的催化焰条的典型催化源强。对于火箭,业务中使用较多的一发火箭焰剂的AgI含量为10 g,成核率为1015 g-1,燃烧距离为5 km,则Q火箭=1015×10/5000=2×1012 m-1。对于飞机催化,选择两类典型代表组合,分别为运-7飞机上装载中天/ZY型焰条(简称:运七-中天),焰条含AgI 125 g,成冰率为1015 g-1,燃烧时间为25 min,则成冰核播撒速率为6.67×1013 s-1,航速为200 m·s-1,源强为Q飞机A=6.67×1011 m-1。夏延飞机上装载556厂RDY型焰条(简称:夏延/556),含AgI 11 g,取成冰率为1015 g-1,燃烧时间为12 min,夏延飞机平均航速取为100 m·s-1时,则Q飞机B=11×1015/72000=1.5×1011 m-1(中国气象局,2003)。
这里的研究主要计算冰核及其形成的人工冰晶的位置、运动等催化扩散规律,所以以下的分析重点在2 h内的扩散规律研究,后期人工冰晶长大成雪晶,具有一定落速,其运动过程和下落位置会同本模式结果产生一定的偏差,以下分静止云区和平流云区两种情况进行线源扩散有效区的计算。
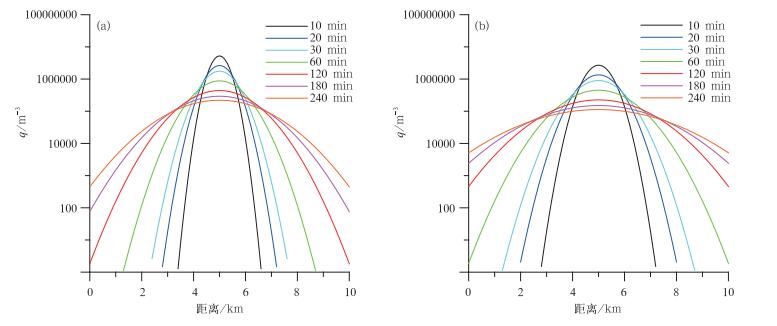
3.1 静止云区火箭飞机单线线源扩散规律及有效区域在式(4) 中u=v=w=0情况下,输入火箭的源强Q火箭为0.2×1013 m-1,成冰率均取1015 g-1,扩散系数分别取kH=70 m2·s-1,kV=35 m2·s-1和kH=140 m2·s-1,kV=70 m2·s-1,得到在静止均匀大气中催化剂瞬时线源扩散在不同时刻的浓度分布如图 4所示(其中横坐标为x轴方向上的距离,纵坐标为催化剂浓度)。
|
图 4 火箭(源强Q火箭=0.2×1013 m-1)单线线源扩散浓度剖面图(纵坐标同图 1) (a)kH=70 m2·s-1, kV=35 m2·s-1;(b)kH=140 m2·s -1, kV=70 m2·s-1 Fig. 4 Diffusion concentration profile of rocket (source concentration Q火箭 is 0.2×1013 m-1) single line of line source (vertical axis same as Fig. 1) (a) kH=70 m2·s-1, kV=35 m2·s-1; (b) kH=140 m2·s-1, kV=70 m2·s-1 |
由图 4可知,对于火箭催化,火箭的中心浓度很高会导致过量催化。在扩散系数为kH=140 m2·s-1, kV=70 m2·s-1时,火箭等的扩散中心浓度较小,扩散范围较大,扩散呈现出一个比较平均的状态,对有效催化较为有利。超过106 m-3的范围达到1 km,维持30 min以上,实用于防雹消雨等要求过量催化的需求。大于104 m-3的显著有效区在2 h内不断扩大,宽度从10 min时的2.1 km,扩大到30 min的3.2 km和60 min的4.2 km。2 h达到显著催化区域宽度可达7 km,有效催化宽度可达9.4 km。
表 1为火箭作业两种扩散系数情况下各时间对应的浓度为104和103 m-3时的剖面宽度。
|
|
表 1 火箭单线线源扩散不同时间下不同浓度的扩散宽度(单位:km) Table 1 Antiaircraft arm single line of line source diffusion width of different concentrations in different time (unit: km) |
一枚火箭的催化剂播撒长度L约为5 km,其在1 h内的显著有效催化区面积S=LD+π/4D2(式中D为扩散宽度),若以D为5.6 km来计算,约为52.6 km2;若以D为7 km来计算,有效面积约为73.5 km2。
下面估算一下该区域内的催化剂平均浓度:扩散区的垂直厚度H平均不到水平宽度的一半,则扩散区的体积约为250 km3,若催化剂主要是在这一空间内,其浓度平均可达1016/250 km3=4×104 m-3。从图 4可见当时(1 h)最大浓度为4×104 m-3,说明该值是可信的。即在1 h后1枚火箭有效催化宽度可达7 km,范围约77 km2,平均催化剂浓度高于104 m-3。即在1 h后1枚火箭有效催化宽度可达7 km,范围约77 km2, 平均催化剂浓度高于104 m-3。
对于飞机催化,在式(4) 中,分别输入运-7飞机源强为Q飞机A=6.67×1011 m-1和夏延飞机上装载556厂RDY型焰条(简称:夏延/556) 源强Q飞机B=1.5×1011 m-1,进行计算,得到“运七-中天飞机”和“夏延-556焰条”两种播撒、两种扩散系数下扩散规律和浓度达104和103 m-3时的剖面宽度,如表 2所示。
|
|
表 2 “运七飞机-中天焰条”和“夏延-556焰条”单线线源扩散不同时间下不同浓度的扩散宽度(单位:km) Table 2 "Yun 7 plane-zhongtian pyrotechnical flare" and "xiayan-556 flare" single line of line source diffusion width of different concentrations in different time (unit: km) |
假定飞机以360 km·h-1的速度飞行,若采用上表中的“运七飞机-中天焰条”,取扩散系数kH=140 m2·s-1,kV=70 m2·s-1,阈值浓度为103 m-3时,扩散宽度为6.6 km,飞机飞行1 h催化的有效面积为S=L×D=360 km·h-1×6.6 km×1 h=2376 km2。
可见,采用单程飞机播撒,在静止云区实际上只催化了很窄的一条,由上表可知,宽度只有不到7 km。实际催化范围相对于目标区云层,一般只有很小一部分被催化了。这样就可能造成催化不充分,影响催化效果, 造成其检验的困难。
3.2 平流下的火箭飞机单线线源扩散及有效区域层状云中一般都有水平气流u, 其速度可达10 m·s-1或更大。在这种状态下,催化剂粒子(或冰晶胚胎)会随风向下游移动。当线源与气流方向垂直时,单线播撒的催化区域和扩散浓度的演变如图 5所示。随着时间变化,条状的催化区不断向下风方移动,同时不断扩散。催化剂虽然会影响下风方大片区域,但在某一时刻只影响很小的条形区域,这与连续线源是完全不同的。计算时取源强为“运七-中天”飞机的源强6.67×1011 m-1,扩散系数为kH=140 m2·s-1,kV=70 m2·s-1,u=10 m·s-1,v=w=0。

|
图 5 平流下瞬时线源单线播撒的催化区浓度及范围随时间的演变 Fig. 5 Single line of line source operation domain concentration and range in advection evolution with time |
由图 5中可见,催化区随时间向下风方移动,在t1=10 min时刻处于距飞行作业轨迹6 km处,到t6=240 min时刻就移到144 km处。
从地理位置来看,播撒线的下风方大范围都受到催化的影响,但是单线催化对一个区域各点的催化是很不充分的。在这一区域中每个点的上空只有少量时段是被催化的,大部分未被催化。在距离d1线上,被催化时段为Δd1/u,在距离d3线上,被催化时段为Δd3/u,其余距离均类似(其中Δd为催化范围,u为风速,Δt为催化时段)。表 3为各时间对应的达到103 m-3阈值的催化时段和范围。从表 3中可看到,在关注的时间范围内,达到阈值浓度的范围一直在增大,催化的时段也随之变长。
|
|
表 3 平流下瞬时线源单线播撒各时间的催化区范围和催化时段 Table 3 Single line of line source operation domain range and time in advection of separate time |
如果可催化云区宽度为50 km,平流速度为10 m·s-1,则在每个点上可催化云区持续的时段,相当于人工增雨中可催化的降雨时段,为50 km/(10 m·s-1)=5000 s=83 min。但实际催化的时段在各点不同,如表 3所示,在作业点下风方18、36、72和108 km处分别为应为8、11、14.4和16.4 min,分别占降雨时段83 min的9.64%、13.25%、17.35%和19.76%。如果催化云区(催化时段)能增雨40%,那么在单线播撒下,各点的增雨率只有3.856%、5.3%、6.94%和7.904%,效果较差。
当线源同气流平行时,线源的扩散基本不变,只是向下风方向平流。如果飞机平行于气流飞行,在顺风时飞行速度提高到va+u,源强就减小u/va倍;在逆风时飞行速度减小为va-u,源强就增大u/va倍。
3.3 静止云区多线瞬时线源扩散及有效区域对于锋面云系,一般宽100 km, 可催化区宽50 km,由上面计算可知,一般飞机作单线播撒时,催化区的宽度在1 h扩展到6.6 km, 那么只催化了13.2%的区域。如果采用7条平行线播撒,那么催化区的宽度可达46.2 km, 可以基本覆盖整个可催化区。因此在大面积上实施人工影响云和降水作业时,采用多架飞机同时飞行或一架飞机穿行,或是多枚火箭催化作业,均可形成多条线源。下面分静止云区和平流不同情况,研究计算多条线源扩散的扩散范围和浓度分布。
为了使催化区充分催化,实际中多采用耕作式(或称蛇形)播撒,即在一定范围内以一定间隔来回飞行播撒,前文计算飞机催化作业在1 h内达到的扩散宽度为6.6 km,下面以6.6 km为间距的3个来回的耕作式飞行播撒路线,以此种飞行设计为例,计算多条线源扩散的扩散范围和浓度分布。
采用3条平行瞬时线源,扩散系数为kH=140 m2·s-1, kV=70 m2·s-1时,取3种不同的源强,即火箭Q=2×1012 m-1,运七-中天Q=6.7×1011 m-1,夏延-556 Q=1.5×1011 m-1。用式(5) 计算其催化剂浓度分布和变化,列于图 6。由于浓度q同源强Q成正比,所以不同源强的结果基本相似,图 6中以中天Q=6.7×1011 m-1为标准,得到大于104和103 m-3(实线和虚线)的催化范围随时间变化。对于火箭Q值大了3倍,所以大于104和103 m-3的位置应在图 6中3.3×103和3.3×102 m-3的地方。而夏延-556的源强相当于中天的0.22倍,所以大于104和103 m-3的位置应在图 6中4.5×104和4.5×103 m-3的地方。在图 6中已用不同颜色的实和虚线标出。

|
图 6 瞬时平行多线扩散的浓度垂直剖面演变示意图 (其中纵坐标同图 1;红色虚线和实线为运七-中天飞机的103和104 m-3的浓度阈值线,绿色虚线和实线为夏延-556飞机的103和104 m-3的浓度阈值线,橙色虚线和实线为火箭的103和104 m-3的浓度阈值线) Fig. 6 Parallel lines of line source diffusion concentration vertical profile evolution with time (The vertical axis same as Fig. 1, the red dotted and solid line is the threshold value of Yun 7-zhongtian 103 and 104 m-3, the green dotted and solid line is the threshold value of Xiayan-556 103 and 104 m-3, and the orange dotted and solid line is the threshold value of rocket 103 and 104 m-3) |
由图 6可以得到以下结论:(1) 初始阶段,即1 h之前,扩散范围是3条独立的扩散,以“运七-中天”为例,每条扩散范围达到有效催化阈值的宽度为3.1 km,每两条之间相距3.7 km。(2) 到1 h,以“运七-中天”为例,整个区域都达到有效催化的阈值浓度,扩散范围可达到19.6 km;对于火箭,扩散范围更大,可达21.2 km;对于“夏延-556”,因为源强浓度较小,3条扩散带之间还有一定的空隙和间隔,间隔大约不到1 km。(3)1 h之后,3种播撒方式都可使整个区域均达到有效催化的阈值浓度,只有边缘区域浓度下降较快。由此可见,这种播撒方式可以保证在一定水平范围内、一段时间内始终保持要求的浓度值。
3.4 平流下多线瞬时线源扩散及有效区域在层状云中,考虑水平风速情况下,瞬间多线“播撒”后,在输入的源浓度为运七-中天的浓度Q飞机A为6.67×1011m-1,成冰率为1015 g-1,扩散系数kH=140 m2·s-1, kV=70 m2·s-1,线间距离为6.6 km时,不同时刻催化区的位置和浓度分布如图 7所示。

|
图 7 瞬间多线“耕作”后,催化区的位置和浓度分布演变 (其中纵坐标同图 1;红色虚线为运七-中天的103 m-3的浓度阈值线,绿色虚线为夏延-556飞机的103 m-3的浓度阈值线,橙色虚线为火箭的103 m-3的浓度阈值线) Fig. 7 Evolution of operation domain location and concentration distribution after multi-line seeding (The red dotted line is the threshold value of Yun 7-zhongtian 103 m-3, the green dotted line is the threshold value of Xiayan-556 103 m-3, and the orange dotted line is the threshold value of rocket 103 m-3, vertical axis same as Fig. 1) |
图中以3条平行瞬时线源播撒为例,扩散10 min时,为分散的3个催化区;扩散60 min时,线间浓度明显变大,达到103 m-3,边缘浓度依然较低,最大浓度也有所下降,催化区域开始变得连贯。扩散120 min时,3个催化区中间的浓度持续增大,达到104 m-3以上,催化区域连贯且均匀。对比单线播撒时达到阈值浓度区域较小的情况,多线播撒形成的催化区宽度大,两侧扩散浓度的减低要小得多,维持的时间也长得多。这与我们实际作业中希望得到的一个区域内催化扩散均匀连续,且能够维持在有效催化浓度的情况十分吻合。
从地面各点来看,在距飞行位置6 km处,从略早于10 min时起,有3段各为Δd1/u(Δd1为10 min时单线扩散的宽度)的时段被催化,间隔为9 km/(10 m·s-1)=900 s。在距飞行位置72 km处,从略早于60 min时起有21.6 km的范围,即2160 s的时段连续被催化。如果可催化区为50 km宽,则经过每点的可催化时段应为50 km/(10 m·s-1)=5000 s。而在3次耕作播撒中,实际各点被催化的时段等于或小于2160 s,即只占了可催化时段的43.2%。如果采用5次耕作播撒,则实际催化时段可达3760 s,即占可催化时段的75.2%。如果催化云区可增雨20%,那么采用5次穿飞播撒的增雨率可达20%×75.2%=15.04%。考虑到多线播撒的催化剂维持时间大大加长,在距飞行位置超过72 km后的区域仍会维持一定的催化时段,所以它的实际增雨率远比单线播撒要高。
4 飞机移动点源播撒扩散规律及有效区域飞机播撒在实际作业中一般要持续几个小时,前面将飞机飞行播撒近似为瞬时线源,同实际还是有较大的出入,在飞机人工增雨实际催化过程,飞行中飞机播撒催化剂为移动点源的单点移动播撒。因此,为更好的接近实际播撒过程,作为移动点源单点移动播撒考虑更为恰当。结合以上研究,进行更接近实际的飞机不同情况下的扩散变化规律及有效区域范围计算研究。
在单点移动播撒扩散计算研究中,输入的源浓度为夏延-556的浓度Q飞机B=1.5×1011 m-1,成冰率为1015 g-1,扩散系数kH=140 m2·s-1, kV=70 m2·s-1时。
4.1 静止云区的单点(单线及折线)移动播撒在飞机人工增雨实际作业中,所采用的飞机播撒催化剂为移动点源的单点移动播撒。飞机在移动中播撒,各点的起始时刻不同,造成在某一时刻各点所处的扩散阶段是不同的,如图 8所示。

|
图 8 静止云区单点移动播撒的催化区水平分布 Fig. 8 Horizontal distribution of single point remove seeding catalytic domain in static cloud |
图 8中在t0时飞机在d0处,而在d1处的催化剂已经扩散了t1时段t1=(d1-d0)/va,同时在d2至d5处,催化剂扩散了t2到t5时段。垂直于飞机航迹的浓度水平分布相当于图 5中瞬时线源在相应时刻的剖面。通过与单线瞬时线源相同扩散时间的扩散宽度的比较,可以发现单点移动各时间点处的催化剂浓度剖面与单线线源对应时间的催化剂扩散(图 3)是一致的。具体比较数值如表 4所示。
|
|
表 4 单点移动播撒和线源播撒不同时间扩散宽度对比 Table 4 The comparison of single point remove seeding and line source diffusion width in different time |
实际中,飞机有时会做耕作式飞行催化(顺风或逆风),其催化播撒构成单点移动折线播撒。下面研究计算不同情况下的扩散变化及有效区域。
在单点移动折线播撒中,由于各部位扩散阶段不同,某一时刻的催化区,如图 9所示。飞机飞行路线为从t0经t1, t2, …, t10到t16,间距为7 km,直飞段每段为60 km,全程以360 km·h-1航速飞行,直飞段时间间隔为10 min,转弯段时间间隔为1.2 min,扩散系数kH=140 m2·s-1, kV=70 m2·s-1时,催化带的位置则如图 9,t’0, t’1,…,t’11为对应t0, t1,…,t11时间时的催化区位置。飞机此时正处在t’16处,那里是催化带头部。图中各点经历的实际上就是图 8的催化剂浓度变化过程。头部扩散时间很短,催化剂浓度很高。尾部t’0区已经扩散了一个多小时,催化带已经开始合并,线间浓度较高,扩散范围较大,浓度较为平均。从头部到尾部,催化剂的有效水平范围正在扩散增大,且催化的范围和浓度逐渐稳定。

|
图 9 静止云区耕作式单点移动播撒的催化区水平分布 Fig. 9 Horizontal distribution of cultivated flight single point remove seeding catalytic domain in static cloud |
在“耕作式”多线播撒下,虽然每架次催化区的面积不变,但是其形状不是一个6.6 km宽的狭带,而是具有一定长度和宽度的催化区,不仅便于效果的跟踪和检验。更为重要的是,在这一区域内,浓度可以在一定时段内、在一定程度上保持稳定,实现对目标区的充分播撒。而单线狭带的催化剂浓度则会很快地被两边的空气稀释而降低。
4.2 平流下的单点折线移动(飞机耕作飞行)播撒飞机在层状云中实际作业时,是存在水平风速的。当飞机进行耕作式播撒并向上风方转弯掉向,飞机飞行路线为从t0经t1,t2,…,t10到t11,间距为7 km,直飞段每段为60 km,全程以360 km·h-1航速飞行,直飞段时间间隔为10 min,转弯段时间间隔为1.2 min,风向为正东方向,在平流作用下,催化带的位置则如图 10,t0’, t1’,…,t11’为对应t0, t1,…,t11时间时的催化区位置。在直飞段和转弯段,首尾两点的平移距离差为u×(tn-tn-1), 分别为2.4和1.2 km。最后扩散所得的结果如图 10所示。

|
图 10 垂直于平流向上风方向转弯飞行的多线耕作式播撒的飞机催化区分布 Fig. 10 Multi-line cultivated seeding perpendicular to advection and swerve to upwind direction flight operation domain |
由图 10可看出,扩散计算得到平流下的多线平行播撒会与原先设计的飞行航线产生一定偏差,催化带较分散,对于需要播撒催化的目标区域,不能达到充分播撒催化的目的。
然而,当飞机向下风方向转弯飞行时,即飞机飞行路线仍为从t0经t1,t2,…,t10到t11,但风向为正西方向,得到的催化区扩散示意图如图 11所示,扩散区域重叠在一起,只能催化很小一片区域,对目标区也不能达到充分播撒的目的。

|
图 11 垂直于平流向下风方向转弯飞行的多线耕作式播撒的飞机催化区分布 Fig. 11 Multi-line cultivated seeding perpendicular to advection and swerve to downwind direction flight operation domain |
前面的研究,提出了针对高炮、火箭和飞机催化扩散尽可能接近实际的催化扩散计算方案,特别是针对飞机,提出了移动点源的催化扩散方案,建立了飞机催化扩散的计算方案,为检验建立的催化扩散方案,通过陕西一次飞机实际播云作业扩散的卫星监测结果,来检验计算方案和结果的准确性。
2000年3月14日陕西进行了一次AgI飞机人工增雨作业试验,播云80 min(15:35) 后,从NOAA-14卫星监测和分析显示,播云后的云顶形成了一条清晰的云沟(余兴,2005b)。
此次人工增雨作业时间为14:15—15:49,平均飞行速度为360 km·h-1,播云高度为4.35 km,温度为-10℃,播云94 min耗AgI 1200 g;云底高度为2.2 km;温度为2℃;云顶高度为4.5~5.3 km;温度约为-17~-13℃,成冰率为1015 g-1。根据这些实际参量,计算得到源浓度2.13×1012 m-1,扩散系数分别为kH=70 m2·s-1,kV=35 m2·s-1和kH=140 m2·s-1,kV=70 m2·s-1时,输入1.4节中式(6),计算分别得到扩散区域两组图(见图 12),其中O、A、B、C、D、E、F、G、H为云迹线的拐点编号。

|
图 12 2000年3月14日陕西飞机催化实际个例扩散计算图 (a)扩散系数kH=70 m2·s-1, kV=35 m2·s-1; (b)kH=140 m2·s-1, kV=70 m2·s-1(图中细实线为飞机的飞行轨迹) Fig. 12 The case of Shaanxi diffusion diagram on 14 March 2000 simulated by model (a) diffusion factor equal to kH=70 m2·s-1, kV=35 m2·s-1, (b) kH=140 m2·s-1, kV=70 m2·s-1, of which the solid line is the flight track of plane |
图 13给出当日NOAA卫星实测的播撒扩散的云际线及选取的剖面位置(戴进,2006)。

|
图 13 2000年3月14日NOAA三通道合成云际线图像(戴进,2006) Fig. 13 Cloud track of NOAA three channel synthesized image on 14 March 2000 |
对比本方案计算结果和与NOAA卫星实测的播撒扩散的云际线的长度和剖面宽度(图 12和图 13),分析检验本方案计算的准确度。表 5和表 6给出本方案计算的云迹线长度和剖面宽度与卫星实测数据的对比,其中宽度对比时计算了线源在剖面对应时间时的扩散宽度,作为对比。
|
|
表 5 本方案计算的播散云际线长度与NOAA卫星实测结果对比 Table 5 Comparison of seeding cloud track length simulated by model and observed by NOAA satellite |
|
|
表 6 本方案计算的播撒扩散云际线剖面宽度与NOAA卫星实测结果对比 Table 6 Comparison of seeding cloud track profile width simulated by model and observed by NOAA satellite |
由表 5和表 6可以看出,计算的云迹线长度与实测的基本一致。但宽度上有一定差别,移动点源和瞬时线源计算的扩散宽度最大值比实测的要小。计算的扩散宽度一直呈现递减的趋势,与实测的云迹线宽度的先增大后减小有所不同。从表中数值来看,移动点源和瞬时线源计算的数值在77~24 min时间段内的数值变化起伏要小于实测的结果,移动点源和瞬时线源计算的结果呈现出的是一个均匀的、稳定的扩散,也是我们在人工影响天气作业中所希望得到的结果。
当扩散系数kH=70 m2·s-1, kV=35 m2·s-1时,移动点源和瞬时线源计算的偏小。当扩散系数kH=140 m2·s-1, kV=70 m2·s-1,阈值采用103 m-3时,移动点源和瞬时线源计算的剖面宽度较为接近实测时扩散宽度。故在利用模式计算扩散范围以指导催化作业时应采用kH=140 m2·s-1, kV=70 m2·s-1的湍流系数,比较符合催化作业中的云区的状态,能够获得较为理想的结果。
瞬时线源模拟计算没有考虑风速,且认为飞机一直以360 km·h-1的速度匀速飞行,这与实际作业有一定差别。实际飞行是逆风的,所以源强应比无风时大,这可能是瞬时线源方案计算宽度较小的原因之一。移动点源计算较好地考虑了风速、风向和飞行速度的变化的问题,所以计算的结果更接近实测值。
由表 5和表 6中本方案计算与实测对比分析和检验可以看出,本文提出的移动点源模式扩散计算方案合理,可以很好地模拟计算飞机催化扩散过程,计算的云迹线长度、催化剂扩散宽度方面同实测基本吻合。
6 飞机催化作业目标区充分播撒航线设计根据以上的研究和实例检验分析,在层状云中平流作用下,为达到一定区域内充分播撒,应采用多条平行催化,其播撒飞行航线应设计为如图 14a所示。沿箭头所示,当风向u为正西方向时,飞行应从A经C、B、D,回到A点,依次重复。得到催化区分布应如图 14b图所示,为3条平行分布的催化带。根据计算,当转弯半径和间隔适当时,可实现整个催化区域的完全覆盖,即达到区域内充分播撒的目的。

|
图 14 (a)平流下为达到平行催化带,实现一定区域充分播撒的播撒航线设计;(b)平流下的扩散得到的平行催化带 Fig. 14 The seeding flight design for getting paralleled operation domain in advection, and achieving sufficient seeding in a certain area; (b) the paralleled operation domain in advection |
以下对图 14充分播撒飞行路线设计的一些具体问题,比如从A点到D点的距离等,做一些计算。设飞机航速为va,向下风向以sin-1(u/va)的对地角度飞行,当t2时刻飞C点时,在t1时刻A点播撒的催化剂平移了(t2-t1)·u,它同该时刻播撒的催化剂处在同样的下风方距离上,形成t1-t2催化带。当飞机转弯,在t3时刻到达上风方B点时,t2点已向下移动了(t3-t2)·u,所以,与t2点t3之间的距离为BC+(t3-t2)·u。一般转弯所需时间同(t3-t2)为120 s。如果u= 10 m·s-1,则(t3-t2)·u=1.2 km。如果要保证,BC+(t3-t2)·u=6.6 km,则BC=5.4 km,如果飞机航速为va=100 m·s-1,则
为在实际中更好地应用以上各类催化扩散计算方案,进行催化后的影响范围计算和目标区充分催化的作业设计,开发了软件系统,实现了各种扩散计算的人机交换计算,初步建立了催化扩散计算和充分播撒设计自动化系统,为研究各类扩散及业务实际应用提供了方便,初步实现的软件界面见图 15。

|
图 15 作业催化扩散区自动计算和充分播撒作业设计软件系统及实例 Fig. 15 Automatic calulation of operation diffusion area and software system and examples of sufficient seeding work design |
图 15a所给出的是2013年4月4日在河北的一次飞机播云飞行轨迹和扩散结果图。此次播云作业飞机播撒催化剂时间为22:05—23:05,根据探空资料输入风速为12 m·s-1,风向为西南风,与正南方向夹角50°,在扩散2 h后所得的扩散结果如图 15a所示。图 15b是2013年4月19日在河北的一次飞机播云飞机轨迹和扩散结果图。此次播云催化作业飞机播撒催化时间从10:05—12:05,根据探空资料输入风速为16 m·s-1,风向为西南风,与正南方向夹角70°,在扩散2 h后所得的扩散结果如图 15b所示。
该软件可方便且较为准确地计算飞机、高炮和火箭实际作业时催化剂在云中扩散的范围、浓度及其随时间的演变,同时可进行针对不同目标区进行充分播撒催化的作业设计,且输出结果直观简明,对实际的人工影响天气飞机、高炮和火箭播云作业指挥和作业后的效果分析将能够提供很大的作用和帮助。
8 结论和讨论本文通过点源、线源、移动点源等情况下的扩散计算模式,探讨了不同情况扩散区域计算和充分播撒飞机飞行航线等作业设计问题。得到了以下结论。
(1) 高炮作业可视为点源的扩散,单个高炮作业,由于炮弹成核率很低,达到有效浓度维持时间很短,只有不到5 min,范围也很小,只有0.5 km。多个炮弹间隔一定距离的作业,则可在一定范围、一定时段里维持有效浓度,如在1.5 km范围内相距300 m的5发炮弹维持有效催化超过4 min。所以实际作业中应当采用多发炮弹密集作业,比较有利于浓度和催化范围的维持。
(2) 火箭和飞机作业可作为线源扩散计算讨论,火箭1 h内达到有效催化浓度的宽度约为7 km,运七-中天飞机1 h内达到有效催化浓度的宽度约为6.6 km。在一定飞行间距下,多线播撒可能保证整个区域的有效催化。
(3) 飞机播撒计算的最优方案是单点移动播撒扩散,其每点与点源扩散的每个对应时间的扩散是相同的情况。实际中通常采用的单点移动“s”耕作式播撒,在一定风速作用下,扩散区域会分散或重叠,不利于充分播撒。
(4) 实现目标区无间隙均匀充分播撒的飞机播撒最佳航线设计是“8”字形飞行播撒路线,飞机在原地做“8”字形来回穿飞,可使一定目标催化区域在平流下得到充分播撒。在这样的设计下,我们可以获得成片的催化区在指定时间段内的充分催化,使目标区得到更加充分的催化。
(5) 将本文提出的单点移动播撒模式计算结果与一次飞机播云作业的实测结果做了对比,检验了该方案的合理性,通过对比试验发现采用扩散系数较大时,与实际作业时的云的情况更加接近,能够得到更合理的结果。
(6) 在研究基础上利用不同情况下的扩散计算方案和作业设计,研发了自动化软件系统,为人工影响天气高炮、火箭及飞机等催化扩散计算的实际业务应用和和充分播撒作业设计提供了条件。
(7) 文中所用参数(如扩散最大宽度和达到的时间)的具体数值在不同条件下是有差异的,需要进一步研究和观测验证。由于催化剂除了扩散外还必然会形成冰晶,这些人工冰晶还要长大下落,到地面降水的增加还需要一段的时间和过程,因此,上述催化区域和催化时段还不是严格意义上的增雨区域和时段。下一步将通过三维高分辨率的中小尺度双参数云分辨模式的催化模拟,为提高这方面认识提供更多的依据。
戴进, 余兴, 2006. 一次过冷层状云催化云迹微物理特征的卫星遥感分析[J]. 气象学报, 64(5): 622-630. DOI:10.11676/qxxb2006.061 |
申亿铭, 1982a. 过冷云中飞机播撒催化剂的扩散问题.气象科技集刊(2)[M]. 北京: 气象出版社, 17-26.
|
申亿铭, 1982b. 碘化银炮弹在过冷层状云中爆炸后催化剂的扩散问题.气象科学技术集刊(2)[M]. 北京: 气象出版社, 27-29.
|
申亿铭, 1983a. 对流云中点源爆炸催化剂的扩散问题[J]. 气象学报, 41(4): 415-425. |
申亿铭, 1983b. 飞机播撒催化剂的叠加效应[J]. 南京气象学院学报, 2: 239-246. |
申亿铭, 1994. 云中催化剂的扩散[M]. 北京: 气象出版社, 42-134.
|
申亿铭, 陈吉航, 1986. 飞机播撒催化剂扩散问题的数值解法[J]. 气象学报, 44(4): 440-446. DOI:10.11676/qxxb1986.063 |
申亿铭, 陈吉航, 1993. 风速垂直变化对催化剂扩散的影响[J]. 气象, 19(10): 7-11. DOI:10.7519/j.issn.1000-0526.1993.10.002 |
申亿铭, 余康元, 1993. 层状云中垂直线源的扩散问题[J]. 气象, 19(11): 13-17. DOI:10.7519/j.issn.1000-0526.1993.11.003 |
史月琴. 2008. 华南冷锋云降水微物理过程及其人工催化机理的数值模拟试验研究. 北京: 北京大学.
|
余兴, 戴进, 2005a. NOAA卫星云图反映播云物理效应[J]. 科学通报, 50(1): 77-83. |
余兴, 戴进, 2005b. 层状云中飞机人工增雨作业间距的研究[J]. 大气科学, 29(3): 465-474. |
余兴, 樊鹏, 王晓玲, 等, 1998. 层状云中非垂直多条撒播线源催化剂扩散的数值模拟[J]. 气象学报, 56(6): 708-723. DOI:10.11676/qxxb1998.065 |
余兴, 王晓玲, 戴进, 2002. 过冷层状云增雨播云有效区域的模拟研究[J]. 气象学报, 60(2): 205-214. DOI:10.11676/qxxb2002.025 |
余兴, 徐小红, 2007. 过冷层状云Agl播云效应区的NOAA卫星反演分析与数值模拟[J]. 自然科学通报, 17(2): 225-232. |
中国气象局, 2003. 中国人工影响天气岗位培训教材[M]. 北京: 气象出版社, 300.
|
Bruintjes R T, Clark T L, Hall W D, 1995. The dispersion of tracer plumes in mountainous regions in central Arizona: Comparisons between observations and Modeling results[J]. Appl Meteor, 34(4): 971-988. DOI:10.1175/1520-0450(1995)034<0971:TDOTPI>2.0.CO;2 |
Hill G E, 1980. Disperion of airborne-realeased silver Iodide in winter orographic clouds[J]. Appl Metetor, 19(8): 978-985. DOI:10.1175/1520-0450(1980)019<0978:DOARSI>2.0.CO;2 |
Holroyd E W, McPartland J T, Super A B, 1988. Observations of silver iodide plumes over the Grand Mesa of Colorado[J]. Appl Meteor, 27(10): 1125-1144. DOI:10.1175/1520-0450(1988)027<1125:OOSIPO>2.0.CO;2 |
Li Zhidong, Pitter R L, 1997. Numerical comparison of two seeding material formation mechanisms on snowfall enhancement from Ground-based Aerosol Generators[J]. Appl Meteor, 36(1): 70-85. DOI:10.1175/1520-0450(1997)036<0070:NCOTIC>2.0.CO;2 |
Schaefer V J, 1946. The production of ice crystals in a cloud of super-cooled water droplets[J]. Science, 104: 457-459. DOI:10.1126/science.104.2707.457 |
 2014, Vol. 40
2014, Vol. 40 